引言

《中国心血管病报告2014》^[1]指出心血管疾病发病率仍持续上升，严重影响人类健康和生活质量，迫切需要快速准确的诊断和治疗手段.近年来，越来越多的研究发现，肺动脉高血压、先天性心脏病和扩张性心肌病等心脏疾病会影响右心室功能变化^{[2, 3]}.心脏磁共振（Cardiac Magnetic Resonance Imaging, CMRI）短轴电影图像时空分辨率好、可重复性高，既可动态观察心动周期内右心室解剖结构，还可准确测量随时间变化的右心室容积，提供心肌运动信息等，目前已成为无创性评价右心室结构及功能的理想方法^[4].

一般情况下，右心室（Right Ventricle, RV）功能可通过右心室分割来实现.与左心室相比，右心室心肌壁薄，与脂肪、乳头肌等组织毗邻，个体结构差异大；此外，部分容积效应和心脏运动常常会导致CMRI短轴电影图像信噪比较差；且右心室与周围组织对比度低^[5]，因而右心室分割一直是临床图像分割中的一大难点与挑战.由于右心室血池和心肌之间对比度较差且结构变异大，传统的分割方法在右心室分割中效果不是太好.例如阈值法不能有效的选择阈值将右心室血池与心肌分开^[6]；形态学方法中形态学算子的大小及形状难以标准化实现右心室精确分割^[7]；图割法易受心肌外部脂肪干扰^[8]；水平集方法受初始轮廓影响大^[9]；主动形状模型（Active Shape Model，ASM）受个体差异及右心室形状变化影响很大^[10].总之，传统的右心室分割方法至今仍未取得突破性进展.自2012 MICCAI（http://www.miccai.org/）举办的右心室分割挑战（Right Ventricle Segmentation Challenge, RVSC）之后，基于卷积神经网络的深度学习在右心室分割中受到越来越多的关注^{[11, 12]}.卷积神经网络深度学习优点在于几乎可以模拟任何形状的曲线，灵活、边界分割比较精确，但该方法需要大量的含有各种特征的训练集，而且右心室个体和内部结构复杂多变；另外，该方法不易穷尽各种特征，计算量巨大.

图谱分割方法将分割转化为配准和融合，是近年来右心室分割的新思路.根据图谱数量，图谱图像分割算法分为单图谱和多图谱.多图谱分割与单图谱分割相比，更加鲁棒、精确，且精度会随着图谱数量的增多而提高^[12].多图谱分割算法的关键在于图谱数量、配准方法和融合策略的选择，其基本思路是分别将每个图谱与目标图像配准以获得目标图像的初步分割结果，对初步分割结果进行融合以提高分割精度.本文利用CMRI短轴电影图像先验知识，在基于归一化互信息的B样条配准的基础上进行COLLATE（Consensus Level, Labeler Accuracy and Truth Estimation）融合，对心脏右心室短轴图像进行自动分割，取得良好的效果.本文将在第一部分重点介绍COLLATE融合算法，然后在第二部分介绍如何利用COLLATE融合多图谱实现CMRI短轴电影图像右心室分割.

1 COLLATE融合

传统的多图谱分割方法在融合阶段多使用加权融合策略或STAPLE（Simultaneous Truth And Performance Level Estimation）融合策略，对大脑或肝脏组织分割结果较好^[13]，但在右心室分割中效果欠佳.本文创新地采用了COLLATE融合算法，该算法基于统计分析，利用数据策略提高分割精度.COLLATE在STAPLE算法的基础上增加了像素一致性概率和区域差异概率评估，更加鲁棒、精确，其理论主要分为变量定义和计算过程步骤两部分^[14]：

1.1 变量定义

假设一幅图像Ⅰ中一共有N个像素点，记i（$i = 1, 2, \cdots, N$）为这幅图像中的单个像素点；对该图像分割后可得到R个粗分割结果，记j（$j = 1, 2, \cdots, R$）为图像的某个分割结果.（1）定义一个N*R的二维矩阵D，表示图像Ⅰ的R个粗分割结果，D_ij表示第j种分割对应的第i个像素的标记值，${D_{ij}} \in \{ 0, 1, \cdots, L - 1\} $, 这里L为可用于标记粗分割结果的标记集合中的分类数目，是大于1的整数值.每个粗分割结果中的每个体素都有确定的对应的标记.（2）定义一个长度为N的一维向量T，表示图像Ⅰ中N个像素的未知的真实分割结果，T_i代表第i个像素的真实分割结果对应的标记值，${T_i} \in \{ 0, 1, \; \cdots, \; L - 1\} $.（3）定义一个具有N个元素的一维向量C，C_i表示每个像素的一致性或混乱性，共有F个一致可能性等级，即${C_i} \in \{ 0, 1, \; \cdots, \; F - 1\} $，其中C_i=0表示像素i具有混乱性，C_i=1表示像素i具有一致性.一致性和混乱性是从相反的方向描述同一个现象，即一致性减少，混乱性就增加.（4）定义$\theta = [{\theta _1}, {\theta _2}, \cdots, {\theta _R}]$，表示与R个粗分割结果对应的性能水平估计；每一个像素θ_j是一个L*L的混合矩阵，矩阵中的每个元素都会量化粗分割j中将真实标记分配给像素的概率.通过上述变量定义，我们将完整数据(D, T, C)对应的概率质量分布函数定义为$f(D, T, C|\theta)$.

1.2 计算过程

为了精确估计真实分割结果的性能水平参数θ，可通过求完整数据$f(D, T, C|\theta)$的对数似然函数的最大值得到，可用(1)式表示：

$ \theta = {\rm{arg}}\mathop {\max }\limits_\theta \ln f(D, T, C|\theta ) $

(1)

在完整数据(D, T, C)中只有D是已知变量，真实分割结果T和一致性水平向量C都是未知变量，因此完整数据的对数似然函数$\ln f(D, T, C|\theta)$是未知的.于是，θ的最大似然估计可通过求非完整数据的对数似然函数$\ln f(D|\theta)$的最大值得到，可用(2)式所示：

$ \theta = {\rm{arg}}\mathop {\max }\limits_\theta \ln f(D|\theta ) $

(2)

COLLATE利用最大期望算法（E-M algorithm，EM）来实现性能水平参数θ的估计.EM是从隐藏变量的数学概率模型中寻找参数的最大似然估计的一种方法，可从非完整数据中对参数进行极大似然估计，简单、稳定、实用.EM通过迭代的方法估计和最大化完整数据的对数似然函数[$\ln f(D, T, C|\theta)$]，从而实现对不完整数据的对数似然函数[$\ln f(D|\theta)$]的最大化.最大期望法分为步骤E和步骤M.

步骤E：假设θ⁽⁰⁾表示参数θ的初始值，计算$\ln f(D, T, C|\theta)$的条件期望，记为$Q(\theta |{\theta ^{(0)}})$，如(3)式所示：

$ Q(\theta |{\theta ^{(0)}}) \equiv E[\ln f(D, T, C|\theta )|D, {\theta ^{(0)}}] = \sum\limits_T {f(D, T, C|\theta )f(D, T, C|{\theta ^{(0)}})} $

(3)

步骤M：在θ的参数空间中求解$Q(\theta |{\theta ^{(0)}})$的最大值，即对于所有$\theta $，找到满足(4)式的${\theta ^{(1)}}$：

$ Q({\theta ^{(1)}}|{\theta ^{(0)}}) \ge Q(\theta |{\theta ^{(0)}}) $

(4)

然后重复步骤E和步骤M，其中在迭代次数为k时，当前估计值为θ^(k)，矩阵D被用于计算完整数据的对数似然函数的条件期望，然后通过最大化$Q(\theta |{\theta ^{(k)}})$来找到估计值θ^(k+1).重复上述步骤，直至收敛，从而获得一个最大似然概率的性能水平参数θ.

2 基于CMRI短轴电影图像的右心室多图谱分割方法 2.1 数据

本论文工作属于回顾性分析，数据来源者均签署知情同意书，随机抽取男性17例、女性13例，年龄涵盖14~75岁，心率覆盖60~120次/min.其中20例随机数据用于图谱制作.CMRI短轴电影图像在GE1.5 T扫描仪（美国通用电气公司）上通过steady-state free precession（SSFP）序列获取，有8~16层，覆盖整个右心室.具体成像参数如下：图像矩阵大小为256*256，成像视野（Field of View, FOV）是360*360 mm²，层厚为6~8 mm，层间距为2~4 mm，每层20~28个时相.

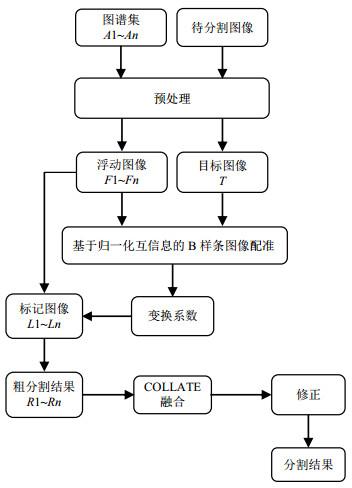
2.2 方法

基于CMRI短轴电影图像的右心室多图谱分割方法主要包括感兴趣区提取、图谱制作、图像配准、图像融合以及结构修正5个步骤，如图 1所示.为了提高计算效率，首先对待分割图像和图谱集A1~An数据进行预处理（n是指图谱集个数，本文定义n为20），分别得到仅含有右心室和左心室的感兴趣区域作为目标图像T和浮动图像F1~Fn，有经验的放射医生对浮动图像F1~Fn中右心室进行手动分割得到标记图像L1~Ln；将目标图像T与浮动图像F1~Fn配准得到配准参数分别应用于对应的标记图像L1~Ln，获得粗分割结果R1~Rn；最后利用COLLATE对粗分割结果R1~Rn融合得到右心室分割结果，从而实现心脏右心室的自动分割.具体过程如下：

2.2.1 感兴趣区域提取

本文首先利用霍夫圆变换确定左心室中心位置^[15]；然后采用大津法对图像进行二值化，将离左心室最近的且面积最大的区域定位为右心室；再通过判断右心室的位置关系，将右心室旋转到左心室水平左侧；最后截取同时包含左右心室的部分图像作为图谱集和待分割图像的感兴趣区域.

2.2.2 图谱集制作

图谱数量的选择是制作图谱过程中一个关键的问题.最初的研究认为图谱数量增加，重叠区域的准确性将随着图谱图像的多变性和配准过程中随机误差的减少而提高，建议在保证计算效率的同时尽量增加图谱图像的数量，以提高最终分割结果的准确性.2009年，Aljabar等人^[16]中通过大量实验发现图谱图像数量在15~25幅之间时，分割结果具有较高的精确度.2012年，Awate等人^[17]通过统计无参回归模型讨论了图谱图像数量对分割结果精度以及分割性能收敛性的影响，结果表明图谱图像数量过多并不能有效提高分割结果精度，反而大大延长处理时间，降低处理效率，并使用40幅图谱图像进行实验，最后也预测图谱图像数量在15~20幅范围内具有良好的精确度.因此本文选用20张结构清晰、受周围组织影响较小的CMRI短轴右心室图像，记为图谱集A1~A20，在保证精确度的同时适当缩短处理时间.然后，有经验的放射科医师手动描绘右心室心内膜得到图谱集对应的右心室分割结果，记为标记图像L1~L20.

2.2.3 基于归一化互信息的B样条图像配准

CMRI短轴电影图像是在四腔心上扫描的垂直于室间隔的4D图像，扫描过程相对比较复杂，但图像中左心室和右心室结构位置及图像灰度相对稳定^[18]，并且通过2.2.1节提取感兴趣区域后，我们感兴趣特征区缩小到仅包含心室，且左右心室位置相对固定；由于心脏在跳动过程中形状变化很大，刚性配准算法不能满足需要.因此，本文以归一化互信息作为相似性测度，采用B样条非刚性配准；在配准过程中，采用梯度下降法进行优化.本文先将每张图谱图像分别与待分割的目标图像配准，记录配准参数；然后将配准参数应用于与图谱图像对应的标记图像上，得到右心室粗分割结果.该方法具有良好的局部控制性，不需要手动标记匹配点，基于灰度互信息就能较好地拟合轮廓曲线，大大的减少了配准时间和和主观因素的影响.

2.2.4 基于COLLATE的配准结果融合

基于前文提出的COLLATE融合策略对经配准过程得到的粗分割结果进行融合.迭代收敛过程控制在20次左右，融合效果较好且用时较短，同时确定截止参数ε=10^-7.基于配准和融合的方法对右心室顶部图像分割较差，在得到最终分割结果之前，需要对顶部图像进行修正，尽量减小误差.

2.2.5 结果修正

右心室顶部血池面积小、心肌薄，但周围存在大面积的脂肪组织；由于脂肪组织与右心室血池的灰度近似，我们在实验中发现配准阶段误将脂肪组织当成右心室，导致右心室最顶部的1~2层最易出现分割错误的情况.CMRI短轴电影图像中，同一时相相邻两层的右心室形状相似，我们基于空间连续性、使用形状对错误层面进行约束修正^[15]，以同一相位相邻正确分割层面的右心室分割结果作为模板，如果相邻图像结果的中心坐标在顶层右心室内，实施基于形状约束的区域生长方法，能够有效防止右心室泄露；如果中心坐标不在顶层图像右心室内，利用圆锥模型进行右心室顶部层面面积估计.

3 结果与讨论 3.1 数据处理及分析

随机选取了10个患者的CMRI短轴电影临床数据，重复2.2节步骤，保存每个数据的右心室最终分割图像；并且根据头文件信息和层厚、像素大小等物理信息，计算舒张末期容积（End Diastolic Volume, EDV）、收缩末期容积（End Systolic Volume, ESV）、每博输出量（Stroke Volume, SV）和射血分数（Ejection Fraction, EF）这4个在临床右心室功能分析中非常关键的参数^[18-20].

采用客观评价方法，首先将使用本文算法的分割结果与使用基于卷积核深度学习算法的全自动分割结果，以及手动分割结果的EDV、ESV、SV和EF进行了比较.其中，深度学习的全自动分割是基于Circle Cardiovascular Imaging公司（http://www.circlecvi.com/）开发的心脏分析软件Cardiovascular Imaging（CVI）实现的.CVI包含基于卷积神经网络深度学习的右心室分割的功能，其结果与手动分割结果非常接近，在全球各大医院得到广泛使用，已有大量文献^[21-23]报道CVI的精准性.本文手动分割结果由有经验的放射科医生描绘右心室心内膜所得，是用于不同算法间比较的金标准.由于本文分割算法和深度学习算法都只考虑了右心室的轮廓，为了保持结果比较的一致性，放射科医师在手动分割时将右心室内部小梁肌、乳头肌等包括在内，仅描述右心室轮廓.

对结果的客观量化指标主要采用（均值±方差）、相关性分析、Bland-Altman一致性分析^[24]、豪斯多夫距离（Hausdorff Distance, HD）^[25]，以及矩阵相似度（Dice Metric, DM）^[26].相关性分析可衡量两个变量因素的相关密切程度，主要用于衡量使用深度学习算法和本文算法自动分割的结果与手动分割结果之间的相关性.Bland-Altman分析是目前一种有效的检验分割效果的评价指标，用于评价深度学习算法和本文算法自动分割结果与手动分割结果之间的一致性.

HD定义为两轮廓间的最大不对称差异，可描述手动分割金标准与本文算法自动分割结果之间的距离差异，定义为(5)式，这里，M和N分别表示手动分割和自动分割的结果轮廓，m和n分别表示M和N中的点，d(m, n)为欧几里得距离.

$ HD(M, N) = \max \left\{ {\mathop {\max }\limits_{m \in M} [\mathop {\min }\limits_{n \in N} d(m, n)], \mathop {\max }\limits_{n \in N} [\mathop {\min }\limits_{m \in M} d(m, n)]} \right\} $

(5)

DM表示本文算法自动分割结果与手动分割结果之间的区域重叠率，可用(6)式定义.A_n表示本文算法自动分割区域；A_m表示所述专家手动分割区域；${A_ \cap } = {A_n} \cap {A_m}$，表示两幅图像的重叠区域，重叠率越高，表示自动分割方法分割出来的组织越接近专家手动勾画出来的金标准，DM越趋近于1.

$ DM({A_n}, {A_m}) = \frac{{2{A_ \cap }}}{{{A_n} + {A_m}}} $

(6)

3.2 结果及分析

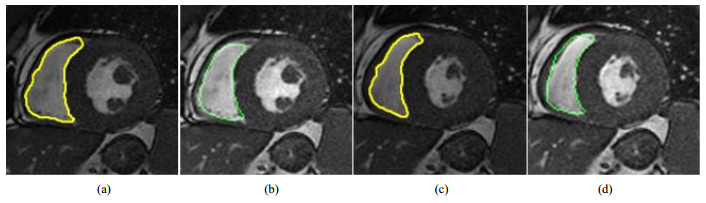
图 2分别展示了一例经典被试在中部右心室舒张末期（End Diastole, ED）和收缩末期（End Systole, ES）时相的手动分割结果和自动分割结果，其中，图 2(a)为ED手动分割结果，即金标准；图 2(b)为使用本文算法的ED自动分割结果；图 2(c)为ES手动分割结果，即金标准；图 2(d)为使用本文算法的ES自动分割结果；从图 2可以看出，本文算法能够较好的适应右心室形状变化，比较精确的勾画右心室.

表 1总结了根据手动分割、基于卷积核神经网络深度学习分割，以及本文提出的基于COLLATE融合多图谱分割的右心室体积计算得到的EDV、ESV、SV和EF.表中数值均以（均值±方差）的形式展示.在这10个数据中，根据手动分割计算出的EDV、ESV、SV和EF分别是（133.7±46.5）mL、（67.5±27.1）mL、（66.2±28.4）mL和49.3%±16.1%；根据深度学习分割计算的EDV、ESV、SV和EF分别是（141.2±45.6）mL、（68.7±26.5）mL、（68.7±26.5）mL和50.0%±27.1%；根据本文多图谱算法分割计算的EDV、ESV、SV和EF分别是（140.7±49.2）mL、（67.3±30.6）mL、（67.3±30.7）mL和46.4%±14.6%.结果显示使用本文算法得到的EDV和SV均值大于手动分割结果；ESV均值与手动分割结果接近；EF均值比手动分割结果均值小.使用深度学习算法得到的EDV、ESV和SV和EF的均值大于手动分割结果.与深度学习算法相比，使用本文算法得到的EDV、ESV和SV均值更接近手动分割结果，标准偏差都是深度学习算法更接近手动分割；虽然使用深度学习算法得到的EF均值更接近手动分割结果，但是其偏差却很大，几乎是本文算法的两倍.分别对手动分割与深度学习算法、手动分割与本文算法计算的EDV、ESV、SV和EF做配对T检验，均无显著差异（p > 0.05）.

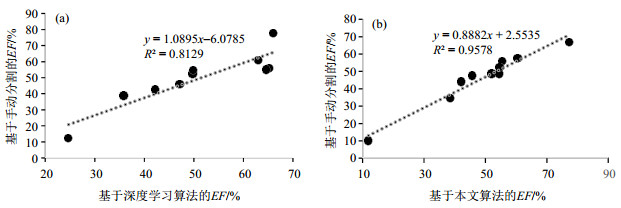
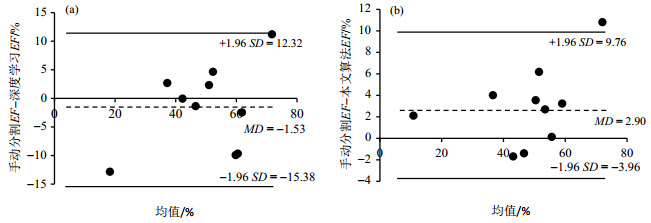
针对EF这个临床上最关键的指标，我们进一步比较了使用本文算法和深度学习算法得到的结果分别与手动分割方法的相关性（图 3）和一致性（图 4）.图 3(a)和图 3(b)显示使用深度学习算法和本文算法与手动分割计算得到的EF的相关性（R²）分别为0.812 9和0.957 8，由此可见，基于本文算法计算出的EF与手动分割的相关性更好.图 4(a)和图 4(b)展示了基于深度学习算法和基于本文算法分别与基于手动分割计算得到的EF的一致性.图 4(a)横轴10个患者数据基于深度学习分割和手动分割得到的EF平均值，纵轴为基于深度学习算法和手动分割得到的10个患者数据的EF的偏差（手动分割EF-深度学习EF）.从图 4(a)可以看到基于深度学习算法计算出的EF普遍比手动分割大，偏差均值（Mean of Deviation, MD，虚线表示）在-1.53%；偏差的标准偏差（Standard Deviation, SD）是7.07%，10个数据有1个数据在（MD±1.96 SD）范围以外；使用本文算法计算出的EF普遍比手动分割小，MD是2.90%，SD是3.50%，10个数据有1个数据在（MD±1.96 SD）范围以外.

通过表 1、图 3以及图 4的分析可知，使用深度学习算法得到的EDV、ESV、SV均值比手动分割得到的均值大；基于本文算法得到的EDV、SV均值比手动分割均值大，ESV均值与手动分割均值接近.基于本文算法得到的EF比手动分割结果偏小，而深度学习算法结果比手动分割结果偏大.基于本文算法得到的EF偏小的原因是ED期体积自动分割比手动分割大，ED期与ES期的体积差（即每搏输出量）却差异不大，而EF的定义为：每博输出量与ED期体积的比值，因此，本文算法的EF偏小.与深度学习分割相比，本文算法与手动分割在EF方差上更加接近，相关性与一致性也更好.

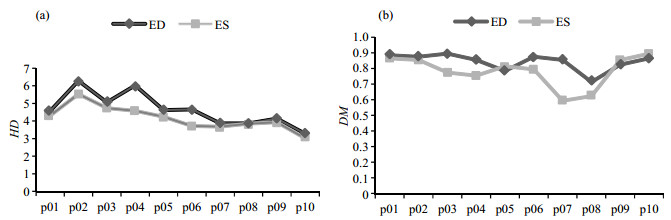
为了验证本文算法的可靠性，我们进一步从图像的角度，对基于本文算法与手动分割得到的分割结果进行了HD和DM比较，如图 5所示.图 5(a)描述了10个被试右心室在ED期和ES期的HD，纵轴数值的绝对值越小，表示基于本文算法的分割轮廓与手动分割轮廓越接近. 图 5(a)显示10个患者的ED和ES期的HD均小于7，并且最小只有3，轮廓相似程度高；在ED期的HD稍微高于ES期，这是由于ED时心肌比ES时更薄，血池与心外膜的脂肪是等高信号组织，在配准过程不易分清，配准难度增大.此外，我们还可以看到HD都是正值，这说明出现最大轮廓差异的地方手工分割轮廓更偏大一点，主要原因右心室大多是月牙形的，在心内膜曲率变化比较大的尖锐的地方，手动分割可以完全将尖端勾画出来，而本文算法中配准过程中采用的B样条配准方法将尖端平滑拉伸导致欠分割. 图 5(b)描述了10个被试右心室在ED和ES期的DM，从图 5(b)中我们可以看到在ED期有8个患者数据的手动分割和自动分割的重合度在0.9左右，另外两个患者数据的手动分割和自动分割的重合度分别是0.8和0.72；在ES期有6个患者数据的手动分割和自动分割的重合度在0.9左右，另外4个患者数据的手动分割和自动分割的重合度分别是0.78、0.72、0.68和0.65，ED期的区域重合度高于ES期的区域重合度，这是由于ED期的体积比ES期体积大，因此重合的部分会更多.

4 结论

本文根据CMRI短轴电影图像特征，对图谱图像集与待分割目标图像采用基于归一化互信息的B样条配准方法得到粗分割结果，然后创新地将COLLATE融合策略对粗分割结果进行融合，并且利用空间连续性修正右心室顶部分割.本文算法在心肌外部脂肪与右心室血池分离且脂肪面积远小于血池面积时具有明显的优势，能适应右心室的弧度较大的边缘和形状、分割结果良好；此外，本文通过空间连续性能够自动识别和筛选出受脂肪组织影响较大的顶部图像，基于形状约束修正顶部右心室分割结果，进一步提高右心室体积计算精度.与基于卷积神经网络深度学习方法相比，本文算法在EDV、ESV、SV计算上具有差不多的性能，但在计算EF时，本文算法与手工分割金标准的一致性和相关性更好.在处理部分尖锐形状的右心室图像时，由于本算法使用B样条配准算法，会将尖锐的边缘平滑化，导致部分图像的分割结果会略大于真实分割结果.通过与经过大量临床验证的深度学习分割方法比较，基于COLLATE融合的多图谱右心室分割同样表现出了良好的性能，这表明多图谱算法有望辅助临床右心室功能诊断.

多图谱分割算法使用配准与融合结合的思路处理分割问题，是图像分割领域中一种新的新尝试，从轮廓的角度进行分割，效果较好.然而，该方法也存在一些不足，比如细节丢失，其分割结果受图谱集、配准及融合方法影响较大等.在今后的多图谱方法中，可更多将边缘灰度或梯度信息、或者右心室本身的形状结构特征引入配准过程中，提高粗分割结果.多图谱分割算法可以从自动配准方法和图谱集选择以及融合算法的优化等方面进行改进，将为图像分割领域提供新的思路和方法.