作为近几年发展起来的一门新兴技术,低场核磁共振技术因其自身的独特性常被应用于农业、酿酒业、石油开采以及食品安全质量检测等领域[1-7].但由于低场核磁共振设备采用的是永磁体,而且应用领域所涉及的外界环境相对比较恶劣,因而采集到的信号信噪比较低,不利于后续的一系列操作.因此,在保证系统稳定性和可靠性的前提下,如何降低噪声、提高有用信号的比例是低场核磁共振技术的关键之一[8].
在众多的去噪方法中,小波变换因其自身具有的独特优势而被广泛使用.它在继承和发展短时傅里叶变换局部化思想的同时,又克服了窗口大小不随频率变化的缺点,提供了一个随频率改变的“时频”窗口,因而成为信号时频分析和处理的理想工具[9].不同于其他的信号处理方法,小波变换可以通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析.它的核心思想是由Mallat于1989年提出的多分辨率信号分解思想[10],具体实现过程为:先将输入信号进行多尺度的分解生成小波分解系数,包括反映低频信息的细节系数(Dj)和反映高频信息的近似系数(Aj),j是分解层数,如图 1(a)所示;然后对分解得到的细节系数Dj进行处理,并通过小波逆变换实现信号的重构,最后输出信号,如图 1(b)所示.
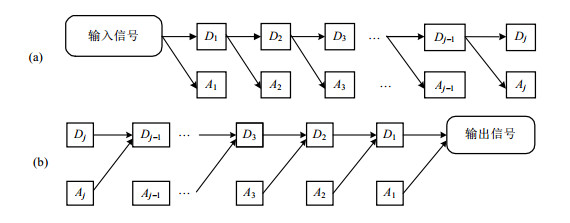
|
图 1 小波变换. (a)分解过程;(b)重构过程 Figure 1 The wavelet transform. (a) The process of signal decomposition; (b) The process of signal reconstruction |
本文主要从以下4个部分介绍利用小波变换对低场核磁共振信号进行去噪的方法:第一部分将介绍3种小波变换形式,分别是连续小波变换、离散小波变换和二进小波变换;第二部分将详细介绍3种小波去噪方法,分别阐述它们的基本思想和执行过程,分析传统方法存在的缺陷,并对众多改进方法作出一一陈述与总结;第三部分将介绍4个常用去噪效果评价参数及其计算方法;第四部分将结合仿真实验对3种方法进行分析总结.
1 理论背景低场核磁共振采集到的信号呈多指数衰减,称为自由感应衰减(Free Induction Decay, FID)信号.该信号前端衰减较快,包含有绝大部分的有用信息,因此,在去噪的过程中要避免这部分信息的丢失;FID后端平坦部分信息量几乎衰减为0,基本全被噪声污染.单一时域或频域的分析方法无法直观地反映出信号幅度及相位随时间和频率变化的情况,也就无法实现对FID信号的有效去噪[11].而小波变换作为一种时频分析工具可以将一维信号放在二维的时频平面上进行分析,从而更加直观地表示脉冲信号的时频特征[12].小波变换中所使用的小波基之间存在着尺度(频率)和平移(时间)上的关系,也就是一组小波基既可以反映时域信息又可以反映频域信息,这使得它在处理FID信号时有明显的优势.常见的3种小波变换形式为:连续小波变换、离散小波变换和二进小波变换,下面就分别对这3种小波变换形式进行介绍.
1.1 连续小波变换通常,对一个信号
| $ {W_f}(\tau ,s) = \frac{1}{{\sqrt {|s|} }}\int_{ - \infty }^{ + \infty } {f(t)} \mathit{\Psi }(\frac{{t - \tau }}{s}{\rm{)d}}t $ | (1) |
其中,τ称为平移因子,s被称为尺度因子,小波基函数
| $ {\mathit{\Psi }_{\tau ,s}}(t) = \frac{1}{{\sqrt {|s|} }}\mathit{\Psi }(\frac{{t - \tau }}{s}) $ | (2) |
因此,原始信号可以通过小波逆变换(Inverse Wavelet Transform, IWT)从分解后的小波系数中重建出来
| $ f(t) = \frac{1}{{{C_\Psi }}}\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {{W_f}(\tau ,s)} } {\mathit{\Psi }_{\tau ,s}}(t){\rm{d}}t\frac{{{\rm{d}}s}}{{{s^2}}} $ | (3) |
其中,
| $ {C_\mathit{\Psi }} = \int_0^{ + \infty } {\frac{{{\rm{|}}\mathit{\Psi }{\rm{(}}\omega {\rm{)|}}}}{\omega }} \,{\rm{d}}\omega $ | (4) |
其中,
连续小波变换中的尺度因子s和平移因子τ均为连续变换,会产生冗余信息,而离散小波变换对这两个尺度因子进行离散化.令
| $ {\mathit{\Psi }_{j,k}}(t) = s_0^{ - \frac{j}{2}}\mathit{\Psi }(s_0^{ - j}t - k{\tau _0}) $ | (5) |
一般取
| $ f(t) = c\sum\limits_{ - \infty }^{ + \infty } {\sum\limits_{ - \infty }^{ + \infty } {{C_{j,k}}} } {\mathit{\Psi }_{j,k}}(t) $ | (6) |
其中,c是常数,
| $ {C_{j,k}} = \int_{ - \infty }^{ + \infty } {f(t)} \overline {{\mathit{\Psi }_{j,k}}(t)} \,{\rm{d}}t $ | (7) |
二进小波变换是介于连续小波变换与离散小波变换之间,它是只对尺度因子s进行离散化,但保持平移因子τ连续取值,以保持时间域上的平移不变性,被广泛用于信号奇异性检测及图像处理中.
令
| $ {\mathit{\Psi }_{{2^j},\tau }}(t) = {2^{ - \frac{j}{2}}}\mathit{\Psi }[{2^{ - j}}(t - \tau )] $ | (8) |
二进小波变换为
| $ {W_f}({2^j},\tau ) = {2^{ - \frac{j}{2}}}\int_{ - \infty }^{ + \infty } {f(t)} \overline {\mathit{\Psi }[{2^{ - j}}(t - \tau )]} \,{\rm{d}}t $ | (9) |
低场核磁共振采集到的信号会受到来源复杂的噪声污染,我们通常采用加性高斯白噪声来模拟实际过程中的噪声污染.目前,用于低场核磁共振信号去噪的小波变换方法主要包括Donoho等人[13]提出的阈值去噪方法、Mallat[10]提出的模极大值去噪方法和Witkin[14]提出的小波系数相关性去噪方法.
2.1 小波阈值去噪小波阈值去噪的思想是在得到低场核磁共振测量的数据后,首先对这些数据进行小波分解,然后通过设定一个阈值,将低于该阈值的小波系数置为0,保留或收缩高于该阈值的小波系数.去噪过程如图 2所示.
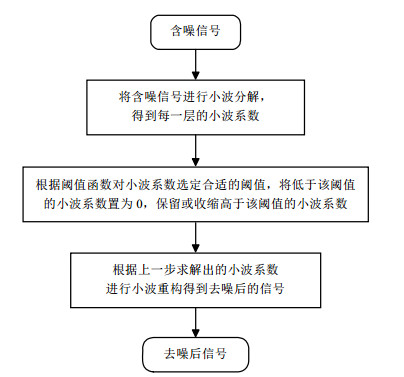
|
图 2 小波阈值去噪法去噪步骤 Figure 2 The denoising steps of the wavelet threshold method |
可以看出,上述步骤中最关键在于第二步,包括阈值和阈值函数的选取.阈值l的选取方法最早由Donoho[15]提出
| $ \lambda = \sigma \sqrt {2\ln N} $ | (10) |
其中N为采集到的低场核磁共振信号长度,σ为估计的噪声方差.但由于该阈值对所有尺度进行了统一处理,因此不可避免地去除掉了一些脉冲信号前端的有用信息,并且该方法过分依赖于阈值的选取.
阈值函数的传统选取方法有两种:软阈值函数和硬阈值函数,但这两种选取办法均存在一定的问题.软阈值函数的表达式如下:
| $ {y_s}(x) = \left\{ \begin{array}{l} {\mathop{\rm sgn}} (x)(|x|-\lambda ), {\rm{ }}|x| \ge \lambda \\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\; |x| < \lambda \end{array} \right. $ | (11) |
其中,sgn(x)为符合函数,即当x > 0时,函数值为1;当x < 0时,函数值为-1;当x
= 0时,函数值为0.可以看出,利用这种方法得到的
硬阈值函数的表达式如下:
| $ {y_h}(x) = \left\{ \begin{array}{l} x, \; |x| \ge \lambda \\ 0, \; |x| < \lambda \end{array} \right. $ | (12) |
显然,它的问题是函数的不连续性以及在
为了解决传统选取方法中存在的问题,研究者们相继提出了众多方法.针对低场核磁共振的回波信号幅度较低、回波串信噪比较差的问题,2010年,Xie等人[16]将多分辨Stein无偏风险估计(Stein Unbiased Risk Evaluation, SURE)算法应用于核磁共振信号去噪.在SURE算法的基础上,通过最小风险估计提出一种新的自适应阈值计算方法,从相关系数图版中确定尺度因子和分解层次,依据噪声在不同分解层次上的差异取不同的阈值对回波信号去噪.结果表明,原信号中的噪声分量得到了很好的压制,信噪比由去噪前的7.822 dB变为了去噪后的16.358 dB.2011年,Ma等人[17]提出一种新的基于小波阈值的去噪算法.根据FID信号的多指数衰减特征,将低场核磁共振信号分解成多个子窗口信号,每一个子窗口信号都是原信号的一部分.因不同的子窗口信号长度不同而选用不同的小波基进行自适应阈值函数去噪.实验结果表明[17],比起中值滤波、传统小波变换和有限长单位冲激响应(Finite Impulse Response, FIR)滤波,该方法能大幅提高信噪比、有效保留有用信息、均方根误差在多组实验中均为最小值.它不仅成功去除噪声,而且去噪后的信号也更加平滑,非常适合核磁共振信号的去噪.2013年,Xiao等人[18]结合文献[19]和文献[20]提出正则化-启发式阈值算法(Regularization Heursure, R-Heursure),通过对目标函数
基于交替投影的模极大值去噪算法最早由Mallat[21, 22]提出,是通过在Hilbert空间的多个闭凸集之间进行反复交替投影来提高算法的重构精度.利用该算法对低场核磁共振信号进行去噪的核心是,根据采集到的低场核磁共振信号中的噪声信号与有效信号模极大值点的幅值随尺度变化呈现出的变化趋势不同,而成功将噪声滤除.一般来说,回波信号中的有效信号模极大值点的幅值随尺度的增加呈现增加趋势,相反,其中的噪声信号模极大值点的幅值随尺度的增加呈现减小趋势.算法过程如图 3所示.

|
图 3 模极大值去噪法去噪步骤 Figure 3 The denoising steps of the wavelet transform modulus maximum method |
但最早提出的这种算法存在如下缺点[23]:1.程序复杂,计算量大;2.收敛速度取决于所用小波的性质,导致收敛速度较慢;3.当原始小波变换发生跃变时,会有类似Gibbs的伪震荡现象出现.
为了解决上述问题,诸多学者在原有算法基础上进行了改进.2008年,Wang等人[24]提出了一种新的结合阈值选取的模极大值去噪方法——基于相关系数最大原则的最优小波基选择方法,它利用目前多种优良的小波基函数进行分解实验,对于选定的小波基函数和消失矩阶数、尺度参数,比较其对应小波变换结果(即分解并重构得到的信号)与参照信号的相关系数, 选择相关系数最大的小波基函数及相应的消失矩阶数、尺度参数作为最优小波基函数,并将该方法用于临床获得的神经胶质瘤FID数据,对选定的病变组织的FID信号施加改进的去噪方法,结果显示[24],门限阈值、“one”小波分解层次内噪声估计方法的阈值策略是最优的方案,该方法可对神经胶质瘤病例的FID信号进行有效去噪.2015年,Gao等人[25]根据核磁共振测井自旋回波信号的特点,进行了模极大值小波变换,通过实测的1 000组数据生成了回波信号,对其进行最大层数为4的分解,设置交替投影的迭代次数为6次.实验表明[25],经过3层分解后,近似系数既能反映出原始信号的特征信息,且细节系数分布紧密,表明信号噪声较集中;通过交叉投影重构后的信号光滑、平稳,很好地体现了去噪后的信号与原始信号的相近性.同年,Sun等人[26]提出在二进小波变换的原理上将小波模极大值重构算法与自适应滤波算法相结合的方法.通过对仿真仿真数据进行去噪得出,相较于单独使用自适应滤波算法和小波模极大值重构算法,结合后的算法处理后所得的信号曲线的平滑度更好,可以很好地将噪声与信号分离开来,同时信噪比达到最高且最可信[26].实测数据处理同样表明,在地下水含量未知的条件下该结合算法获得了较好的去噪效果.
2.3 小波系数相关性去噪大多数基于小波去噪的非线性阈值规则都假设小波系数是彼此独立的,但实际采集到的低场核磁共振数据的小波变换系数间却是高度依赖的[27].1984年,Witkin[14]首先提出多尺度相关性去噪的思想.利用该方法对低场核磁共振信号去噪的基本思想是在对低场核磁共振采集到的回波信号进行小波分解后,各个尺度上有用信号对应的小波系数具有较强的相关性,尤其在边缘处相关性更加明显;而噪声信号对应的小波系数在尺度间却没有明显的相关性,利用小波系数在不同尺度上对应点的相关性来确定我们所处理的小波系数究竟是信号系数还是噪声系数,从而对小波系数进行取舍,这样处理后的小波系数基本对应着信号的边缘,从而达到对低场核磁共振信号进行去噪的目的[28].对一维信号而言,尺度间相关性的重要程度要大于尺度内相关性的重要程度.小波系数相关性去噪的基本步骤如图 4所示.
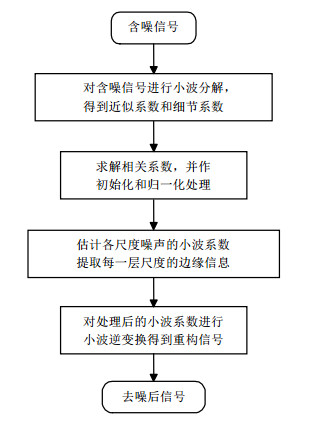
|
图 4 小波系数相关性去噪法去噪步骤 Figure 4 The denoising steps of the correlation of wavelet coefficient method |
2003年,Placidi等人[29]通过结合Xu等人[30]提出的基于信号尺度间相关性的空域相关滤波算法,提出利用Sobel算子提取核磁共振信号中的边界,然后通过计算各尺度间小波系数的相关性对原始信号进行小波变换去噪,再将提取到的边界保存到去噪后所得信号中.通过对0.2 T的实验用磁共振扫描仪添加不同的采集序列得到几组回波串数据,经过去噪,信噪比由去噪前的12 dB提高到了20 dB,并且在大幅度去除噪声的同时边界得到了很好地保留,一些细节信息被放大,这证明了该方法的有效性.2003年,Zhang[31]和Bao[32]等人通过将相邻尺度的小波系数相乘来构造空域相关函数,提出直接对尺度间系数相关性作阈值处理,并成功应用于磁共振信号的去噪,分解层数为4层.对含噪的信号分别用文献[33]中的软阈值方法、文献[34]中的硬阈值方法和该文献提出的方法进行去噪,结果表明,该文献提出的方法能很好地去除感兴趣区域边缘的Gibbs伪影,并能得到很好的量化评价指数.2007年,Zheng等人[35]提出先对小波系数作平移处理,再进行空域相关去噪的方法.实验采用砂砾样品,采样频率和采样点数分别设置为100 k和65 536个,利用低场核磁共振分析测量仪测得样品数据,分别采用基于小波变换的空域相关法和该文献提出的方法对所得信号进行去噪.实验表明,该方法在滤除噪声的同时很好地保留了峰值信息,去噪效果良好.2008年,文献[36]又在文献[35]的基础上给出新的空域相关阈值计算公式.实验采用水作为样品,采样频率和采样点数分别设置为100 k和60 k个,利用低场核磁共振分析测量仪测得样品FID信号;之后对FID信号进行滤波,选用“bior 1.5”小波,分解层数为6层.实验结果表明,相较传统的空域相关滤波法,添加边沿对齐的改进方法处理后的信号边沿无毛刺,波形更加平滑,并通过对纯净信号分别添加5种不同信噪比的高斯白噪声再一次证实添加边沿对齐的空域相关滤波法可将原始信噪比(均大于5 dB)提高10个单位.2015年,Ge等人[37]提出一种混合阈值函数模型,根据信息熵选定小波基函数和分解层数,弥补了软、硬阈值函数的缺点.为了实现不同尺度的阈值最优化,建立了基于信噪比和均方误差的非线性目标函数,将问题转化为寻找最优解的任务,并通过粒子群算法跟踪当前搜索到的最优值来寻找全局最优,以实现算法稳定性和全局收敛性.通过构造多种类型的T2弛豫谱得到核磁共振仿真数据,实验结果表明,比起软、硬阈值去噪算法,改进后的算法可以更好地压制随机噪声,且具有更高的信噪比和更小的均方误差;当核磁共振数据信噪比较小时,去噪效果尤其突出.
3 去噪效果的评价目前,用于去噪效果评价的客观评价标准主要有均方误差(Mean Square Error, MSE)、峰值信噪比(Peak Signal to Noise Ratio, PSNR)、均方根误差(Root Mean Square Error, RMSE)和结构相似性图像评价(Structural Similarity Image Measurement, SSIM).前三者的计算公式如下
| $ MSE = \frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {[X(i, j)}-Y(i, j){]^2}} $ | (13) |
| $ PSNR = 10\lg \frac{{{{({2^n}-1)}^2}}}{{MSE}} $ | (14) |
| $ RMSE = \sqrt {MSE} $ | (15) |
其中M、N分别为图像的高度和宽度;
峰值信噪比的单位是dB,其数值越大表示失真越小,去噪效果越好;而均方根误差的值越小说明去噪效果越好.但许多实验证明,用这3种方法所分析的结果有时与人眼观测到的视觉品质相反.这是因为人眼的视觉对于误差的敏感度并不是绝对的,会受到许多干扰.因此,这里引入2004年由Wang等人[38]提出的SSIM测量参数,它分别从亮度
| $ l(X, Y) = \frac{{2{\mu _X}{\mu _Y} + {C_1}}}{{\mu _X^2 + \mu _Y^2 + {C_1}}} $ | (16) |
| $ c(X, Y) = \frac{{2{\sigma _X}{\sigma _Y} + {C_2}}}{{\sigma _X^2 + \sigma _Y^2 + {C_2}}} $ | (17) |
| $ s(X, Y) = \frac{{{\sigma _{XY}} + {C_3}}}{{{\sigma _X}{\sigma _Y} + {C_3}}} $ | (18) |
其中C1、C2、C3为常数,且值很小,用于避免分母为0的情况;
| $ {\mu _X} = \frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {X(i, j)} } $ | (19) |
| $ {\mu _Y} = \frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {Y(i, j)} } $ | (20) |
| $ \sigma _X^2 = \frac{1}{{M \times N- 1}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[X(i, j)-{\mu _X}]}^2}} } $ | (21) |
| $ \sigma _Y^2 = \frac{1}{{M \times N- 1}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[Y(i, j)-{\mu _Y}]}^2}} } $ | (22) |
| $ {\sigma _{XY}} = \frac{1}{{M \times N- 1}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {[(X(i, j)-{\mu _X}][Y(i, j)-{\mu _Y})]} } $ | (23) |
其中M、N为图像的高度和宽度,于是,对于8位像素图有
| $ SSIM(X, Y) = l(X, Y) \cdot c(X, Y) \cdot s(X, Y) $ | (24) |
本文构造了一个高斯分布的T2弛豫谱,该弛豫谱有两个峰,左峰强度为450 a.u.,右峰强度为1 000 a.u.,如图 5(a)所示.由构造的T2弛豫谱计算出纯净的FID信号,如图 5(b)所示.随机添加功率分别为55 dB、45 dB、35 dB和15 dB的高斯白噪声,得到被污染的信号,如图 6(a)、图 7(a)、图 8(a)和图 9(a)所示;然后分别用小波阈值去噪算法、模极大值去噪算法和基于小波系数相关性的去噪算法进行实验,去噪结果分别如图 6、图 7、图 8和图 9的(b)~(d)所示.

|
图 5 本文构造的T2弛豫谱和纯净的FID仿真信号. (a)构造的T2弛豫谱;(b)纯净的FID仿真信号 Figure 5 Constructed T2 relaxation spectrum and pure FID simulation signal in this research. (a) Constructed T2 relaxation spectrum; (b) Pure FID simulation signal |
由图 6、图 7、图 8和图 9及表 1可以看出,3种去噪算法均能有效地去除夹杂在FID信号中的噪声,并且都获得了较为满意的去噪效果.在数据信噪比较低时,以阈值去噪法最为理想,去噪后的信噪比最高,均方误差也最小;模极大值算法的去噪效果在低信噪比条件下优于基于小波系数相关性算法的去噪效果.而当信噪比较高时,基于小波系数相关性的去噪效果最佳.

|
图 6 添加功率为55 dB的噪声的FID信号和使用3种方法去噪的结果. (a)含功率为55 dB噪声的FID信号;(b)使用阈值去噪算法的处理结果;(c)使用模极大值去噪算法的处理结果;(d)使用小波系数相关性去噪算法处理的结果 Figure 6 FID simulation signal with noise (the power of the noise is 55 dB) and the denoising results by three methods. (a) FID simulation signal with noise of 55 dB energy; (b) The denoising result by using the wavelet threshold denoising method; (c) The denoising result by using the wavelet transform modulus maximum denoising method; (d) The denoising result by using the correlation of wavelet coefficient denoising method |
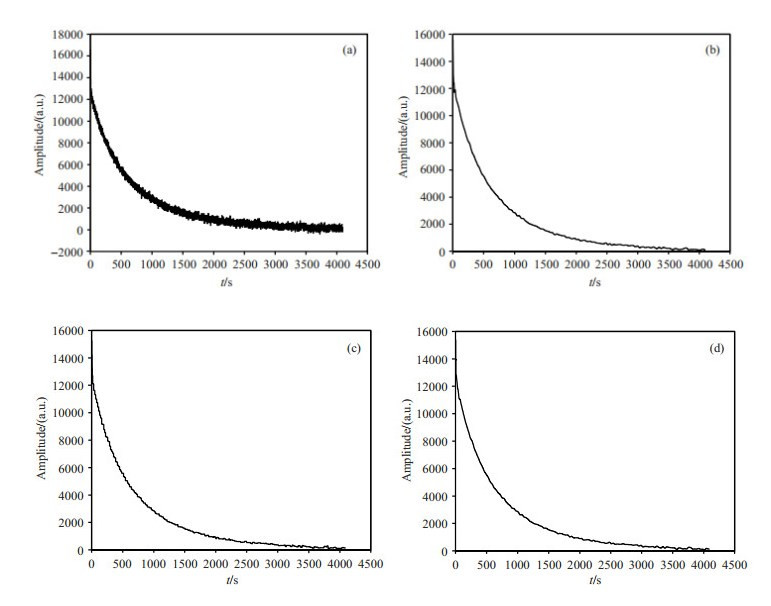
|
图 7 添加功率为45 dB的噪声的FID信号和使用三种方法去噪的结果. (a)含功率为45 dB噪声的FID信号;(b)使用阈值去噪算法的处理结果;(c)使用模极大值去噪算法的处理结果;(d)使用小波系数相关性去噪算法处理的结果 Figure 7 FID simulation signal with noise (the power of the noise is 45 dB) and the denoising results of three methods. (a) FID simulation signal with noise of 45 dB energy; (b) The denoising result by using the wavelet threshold denoising method; (c) The denoising result by using the wavelet transform modulus maximum denoising method; (d) The denoising result by using the correlation of wavelet coefficient denoising method |
|
图 8 添加功率为35 dB的噪声的FID信号和使用三种方法去噪的结果. (a)含功率为35 dB噪声的FID信号;(b)使用阈值去噪算法的处理结果;(c)使用模极大值去噪算法的处理结果;(d)使用小波系数相关性去噪算法处理的结果 Figure 8 FID simulation signal with noise (the power of the noise is 35 dB) and the denoising results of three methods. (a) FID simulation signal with noise of 35 dB energy; (b) The denoising result by using the wavelet threshold denoising method; (c) The denoising result by using the wavelet transform modulus maximum denoising method; (d) The denoising result by using the correlation of wavelet coefficient denoising method |

|
图 9 添加功率为15 dB的噪声的FID信号和使用三种方法去噪的结果. (a)含功率为15 dB噪声的FID信号;(b)使用阈值去噪算法的处理结果;(c)使用模极大值去噪算法的处理结果;(d)使用小波系数相关性去噪算法处理的结果 Figure 9 FID simulation signal with noise (the power of the noise is 15 dB) and the denoising results of three methods. (a) FID simulation signal with noise of 15 dB energy; (b) The denoising result by using the wavelet threshold denoising method; (c) The denoising result by using the wavelet transform modulus maximum denoising method; (d) The denoising result by using the correlation of wavelet coefficient denoising method |
| 表 1 3种方法去噪效果的对比 Table 1 Denoising effects comparison for three denoising methods |
本文主要介绍了3种基于小波变换的低场核磁共振信号去噪方法,并通过多组仿真实验进一步论证了3种方法的有效性.小波阈值去噪算法主要是通过选定合适的阈值对输入信号分解产生的小波系数加以取舍来达到去噪的目的,比较适用于低信噪比数据,去噪范围广,但对信噪比的依赖性较大.模极大值去噪算法主要是根据噪声和信号模极大值点的幅值随尺度变化呈现出相反的变化趋势而成功滤除噪声,它的去噪过程稳定,同样适用于低信噪比数据,对检测信号中的奇异点较为灵敏,但缺点是计算量大,计算时间较长.基于小波系数相关性的去噪算法是根据噪声和信号不同尺度间的小波系数表现出的相关性不同,而将两个组分区别开来,它的去噪计算量、稳定性均介于前两种方法之间,可用来检测信号边缘,更加适用于处理较高信噪比的数据.
| [1] | CARO D D, LIGUORI C, PIETROSANTO A, et al. Hazelnut oil classification by NMR techniques[J]. IEEE T Instrum Meas, 2017, 66(5): 928-934. DOI: 10.1109/TIM.2016.2640438. |
| [2] | CARO D D, LIGUORI C, PIETROSANTO A, et al. Using a SVD-based algorithm for T2 spectrum calculation in TD-NMR application to detect hidden defects in hazelnuts[C]//Instrumentation and Measurement Technology Conference. IEEE, 2017: 1-6. |
| [3] | KIRTIL E, OZTOP M H. 1H nuclear magnetic resonance relaxometry and magnetic resonance imaging and applications in food science and processing[J]. Food Eng Rev, 2016, 8(1): 1-22. DOI: 10.1007/s12393-015-9118-y. |
| [4] | MEMOLI A, ALBANESE D, ESTI M, et al. Effect of bug damage and mold contamination on fatty acids and sterols of hazelnut oil[J]. Eur Food Res Tech, 2017, 243(4): 651-658. DOI: 10.1007/s00217-016-2778-x. |
| [5] |
WANG X H, SUN P, ZHANG X, et al. Application of magnetic resonance technique to quality and safety evaluation of food[J].
Chinese J Magn Reson, 2017, 34(2): 245-256.
王小花, 孙鹏, 张许, 等. 磁共振技术在食品质量与安全研究中的应用[J]. 波谱学杂志, 2017, 34(2): 245-256. |
| [6] |
ZHOU F D, GAO X, CAI J B, et al. Determination of treated and control wood on fiber saturation point by low-field NMR technology[J].
Chinese J Magn Reson, 2017, 34(1): 108-114.
周凡丁, 高鑫, 蔡家斌, 等. 利用低温NMR技术测定木材及其热处理材纤维饱和点[J]. 波谱学杂志, 2017, 34(1): 108-114. |
| [7] | GAUNKAR N G P, NLEBEDIM I C, BULU I, et al. Broadband analysis of response from magnetic cores used in inductive sensors for pulsed nuclear magnetic resonance applications[J]. IEEE T Magn, 2016, 52(7): 1-4. |
| [8] |
WANG H M, NIE S D, WANG Y J. The research progress of de-noising methods in low-field NMR signal[J].
Chinese Journal of Medical Physics, 2013(4): 47-51.
王红敏, 聂生东, 王远军. 低场核磁共振信号降噪方法研究进展[J]. 中国医学物理学杂志, 2013(4): 47-51. |
| [9] | VEER K, AGARWAL R. Wavelet and short-time Fourier transform comparison-based analysis of myoelectric signals[J]. J Appl Stat, 2015, 42(7): 1591-1601. DOI: 10.1080/02664763.2014.1001728. |
| [10] | MALLAT S G. A theory for multiresolution signal decomposition:the wavelet representation[J]. IEEE T Pattern Anal, 1989, 11(7): 674-693. DOI: 10.1109/34.192463. |
| [11] |
YAN T F, YAN T L. Radio spectrum multi-domains analysis based on STFT[J].
Information Technology, 2010, 11: 163-165.
尹天峰, 颜挺利. 基于STFT的无线电频谱信号的多域分析[J]. 信息技术, 2010, 11: 163-165. |
| [12] |
DU Q Y, CHANG Y, QIAN S S, et al. Comparison of time-frequency analysis methods for radio frequency pulses used in magnetic resonance[J].
Chinese J Magn Reson, 2016, 33(4): 646-654.
杜庆阳, 常严, 钱嵩松, 等. 针对磁共振射频脉冲的时频域分析方法比较研究[J]. 波谱学杂志, 2016, 33(4): 646-654. |
| [13] | DONOHO D L, JOHNSTONE I M. Adapting to unknown smoothness via wavelet shrinkage[J]. J Am Stat Assoc, 1995, 90(432): 1200-1224. DOI: 10.1080/01621459.1995.10476626. |
| [14] | WITKIN A P. Scale-space filtering[C]//International Joint Conference on Artificial Intelligence. DBLP, 1983: 1019-1022. https://link.springer.com/article/10.1007%2FBF00135225 |
| [15] | DONOHO D L. De-noising by soft-thresholding[J]. IEEE T Inform Theory, 1995, 41(3): 613-627. DOI: 10.1109/18.382009. |
| [16] |
XIE Q M, XIAO L Z, LIAO G Z. Application of SURE algorithm to echo train de-noising in low field NMR logging[J].
Chinese Journal of Geophysics, 2010, 53(11): 2776-2783.
谢庆明, 肖立志, 廖广志. SURE算法在核磁共振信号去噪中的实现[J]. 地球物理学报, 2010, 53(11): 2776-2783. |
| [17] | MA S B, KONG L, CHEN J J. An improved NMR signal de-noising algorithm based on wavelet transform[J]. Journal of Computational Information Systems, 2011, 7(13): 4651-4659. |
| [18] | XIAO L Z, XIE Q M, XIE R H, et al. Noise reduction for NMR logging with regularization-heursure algorithm[J]. Journal of Computational Information Systems, 2013, 56(11): 3943-3952. |
| [19] |
PAN Q, MENG J L, ZHANG L, et al. Wavelet filtering method and its application[J].
Journal of Electronics & Information Technology, 2007, 29(1): 236-242.
潘泉, 孟晋丽, 张磊, 等. 小波滤波方法及应用[J]. 电子与信息学报, 2007, 29(1): 236-242. |
| [20] | XIE R H, WU Y B, LIU K, et al. Using wavelet domain adaptive filtering to improve signal to noise ratio of nuclear magnetic resonance log data from tight gas sands[J]. Geophys Prospect, 2016, 64(3): 689-699. DOI: 10.1111/gpr.2016.64.issue-3. |
| [21] | MALLAT S, ZHONG S F. Characterization of signals from multiscale edges[J]. IEEE T Pattern Anal, 1992, 14(7): 710-732. DOI: 10.1109/34.142909. |
| [22] | MALLAT S, HWANG W L. Singularity detection and processing with wavelets[J]. IEEE T Inform Theory, 1992, 38(2): 617-643. DOI: 10.1109/18.119727. |
| [23] |
ZHANG X F, XU D Z, QI Z F. Denoising algorithm based on modulus maximum wavelet field[J].
Journal of Data Acquisition and Processing, 2003, 18(3): 315-318.
张小飞, 徐大专, 齐泽锋. 基于模极大值小波域的去噪算法研究[J]. 数据采集与处理, 2003, 18(3): 315-318. DOI: 10.3969/j.issn.1004-9037.2003.03.016. |
| [24] |
WANG X W, DONG G B, XIE G H. A new de-noising method of NMR FID signals based on wavelet transform[J].
Nuclear Electronics & Detection Technology, 2008, 28(2): 365-370.
王希武, 董光波, 谢桂海. 基于小波变换的核磁共振FID信号的去噪方法研究[J]. 核电子学与探测技术, 2008, 28(2): 365-370. DOI: 10.3969/j.issn.0258-0934.2008.02.038. |
| [25] | GAO B K, ZHOU Y H, SUN L C, et al. Modulus maxima wavelet denoising and alternating projection reconstruction of logging signals[J]. Control and Instruments in Chemical Industry, 2015, 42(9): 993-996. |
| [26] |
SUN S Q, MENG Q Y, FANG X C, et al. Noise cancellation algorithm for surface magnetic resonance signals based on self-adaption and reconstruction of wavelet modulus maximum value[J].
Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1642-1651.
孙淑琴, 孟庆云, 方秀成, 等. 基于自适应和小波模极大值重构的地面核磁共振信号噪声压制方法[J]. 吉林大学学报(工), 2015, 45(5): 1642-1651. |
| [27] | SENDUR L, SELESNICK I W. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency[J]. IEEE T Signal Process, 2002, 50(11): 2744-2756. DOI: 10.1109/TSP.2002.804091. |
| [28] | SAEEDI J, MORADI M H, ABEDI A. Image denoising based on fuzzy and intra-scale dependency in wavelet transform domain[C]//International Conference on Pattern Recognition. IEEE Computer Society, 2010: 2672-2675. |
| [29] | PLACIDI G, ALECCI M, SOTGIU A. Post-processing noise removal algorithm for magnetic resonance imaging based on edge detection and wavelet analysis[J]. Physics in Medicine & Biology, 2003, 48(13): 1987-1995. |
| [30] | XU Y S, WEAVER J B, HEALY D M J, et al. Wavelet transform domain filters:a spatially selective noise filtration technique[J]. IEEE T Image Process, 1994, 3(6): 747-758. DOI: 10.1109/83.336245. |
| [31] | ZHANG L, BAO P. Denoising by spatial correlation thresholding[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2003, 13(6): 535-538. |
| [32] | BAO P, ZHANG D. Noise reduction for magnetic resonance images via adaptive multiscale products thresholding[J]. IEEE T Medical Imaging, 2003, 22(9): 1089-1099. DOI: 10.1109/TMI.2003.816958. |
| [33] | CHANG S G, YU B, VETTERLI M. Adaptive wavelet thresholding for image denoising and compression[J]. IEEE T Image Process, 2000, 9(9): 1532-1546. DOI: 10.1109/83.862633. |
| [34] | PAN Q, ZHANG L, DAI G Z, et al. Two denoising methods by wavelet transform[J]. IEEE T Signal Process, 1999, 47(12): 3401-3406. DOI: 10.1109/78.806084. |
| [35] |
ZHENG C X, ZHANG Y M. Method for eliminating noise in nuclear magnetic resonance signals based on wavelet transformation[J].
Analytical Instrumentation, 2007, 26(1): 43-46.
郑传行, 张一鸣. 核磁共振信号的小波变换消噪方法[J]. 分析仪器, 2007, 26(1): 43-46. DOI: 10.3969/j.issn.1001-232X.2007.01.014. |
| [36] | ZHENG C, ZHANG Y M. Low-field pulsed NMR signal denoising based on wavelet transform[C]//Signal Processing and Communications Applications, 2007. Siu 2007. IEEE, 2007: 1-4. http://iopscience.iop.org/1742-2140/11/3/035003/article |
| [37] | GE X M, FAN Y R, LI J T, et al. Noise reduction of nuclear magnetic resonance (NMR) transversal data using improved wavelet transform and exponentially weighted moving average (EWMA)[J]. J Magn Reson, 2015, 251: 71-83. DOI: 10.1016/j.jmr.2014.11.018. |
| [38] | WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment:From error visibility to structural similarity[J]. IEEE T Image Process, 2004, 13(4): 600-612. DOI: 10.1109/TIP.2003.819861. |
 2018, Vol. 35
2018, Vol. 35 
