引言

在核磁共振(NMR)体系中, 磁化矢量从非平衡态恢复到热平衡态的时间分为纵向弛豫时间(T₁)和横向弛豫时间(T₂), 通常情况下, T₁长于T₂.换而言之, 被射频脉冲激发之后的核自旋态的存在时间不会超过T₁.近年来, 多个研究小组相继提出在特殊的分子体系中, 存在一种特殊的量子态—长寿命核自旋单重态, 其寿命(T_S)远远长于相应自旋的T₁, 这主要是由于核自旋单重态具有关于自旋交换反对称的特性, 从而不受分子内偶极-偶极弛豫的影响^[1-13].正是因为核自旋单重态具有寿命较长的优势, 研究者们已经将其成功运用于很多领域, 比如分子的扩散^[14]、慢化学交换^[15]、磁共振成像(MRI)^{[16, 17]}、量子计算^[18]、分子构型和分子动力学^[19]以及混合物的成分分析^[20]等.

目前对长寿命核自旋单重态的研究主要集中在¹H、¹³C和¹⁵N三类原子核上.¹H核体系的核自旋单重态寿命T_S比其T₁提高了几倍~几十倍^{[1, 2, 4, 5, 7, 9, 11-13]}; ¹⁵N₂O中¹⁵N核自旋单重态寿命T_S能超过30 min, 而同等条件下的T₁约为3 min^[6]; 某些¹³C核的T_S也延长到了小时的时间尺度^[21].另外, 用于制备核自旋单重态的自旋数目也在不断增加:从最初的二自旋体系的长寿命核自旋单重态的制备与研究, 发展到三自旋体系和多自旋体系的长寿命核自旋单重态的制备与研究^{[4, 5, 8, 10]}.同时用于研究长寿命核自旋单重态的样品, 也呈现出多样化:有液体样品, 也有气体样品^{[12, 13]}.根据核自旋之间J耦合常数与化学位移差值(Δδ)的大小关系, 用于长寿命核自旋单重态制备的样品体系大致可分为两类:一类是J耦合常数远大于Δδ, 称之为强耦合体系, 另一类是J耦合常数远小于Δδ, 称为弱耦合体系.这两种不同的体系在制备长寿命核自旋单重态时需要应用不同的脉冲序列.

长寿命核自旋单重态制备的实验过程一般都需要经过三个阶段:(ⅰ)长寿命核自旋单重态的获取(需Δδ > J), 主要过程是将核的极化转移到核自旋单重态上; (ⅱ)长寿命核自旋单重态的保存(需Δδ < J), 关键任务是通过消除核自旋之间的化学位移差别来保存长寿命核自旋单重态, 根据具体情形可以通过将样品转换到低场(或零场)区域、或利用化学反应变换分子的对称性、或在高场中施加化学位移去耦脉冲等三种方式实现; (ⅲ)长寿命核自旋单重态的观测, 由于长寿命核自旋单重态自身是相干阶数为0的量子态, 无法直接观测其NMR信号, 需要应用一定的脉冲将长寿命核自旋单重态转化到可观测的单量子相干量子态, 进而观测其NMR信号.由相关理论可知, 对于长寿命核自旋单重态的获得与保存分别需要不同的条件, 即获得时需要核自旋之间具有不为0的Δδ, 而保存时则需要核自旋之间的Δδ近似为0.

由理论计算可知^[5], 对于三自旋体系, 其核自旋单重态的形式可以写成三项相加的形式, 其中每一项为体系中任意两个核自旋形成的核自旋单重态, 有研究者以丙烯酸为例制备了一组特定比例系数组合相加的核自旋单重态.本文对文献[5]中的脉冲序列进行了改进和进一步研究, 给出了适用于任意三自旋弱耦合体系长寿命核自旋单重态制备的参数计算方法, 发现在同一个三自旋体系内核自旋单重态具有多种不同比例系数组合形式, 我们分别以丙烯酸和多巴胺样品自旋体系为例, 进行了理论计算, 得到了多组不同比例系数组合的核自旋单重态, 在计算需要的近似约束条件下选取出两组实验参数, 并以丙烯酸样品为例通过NMR实验制备出了两组长寿命核自旋单重态.实验研究结果表明, 核自旋单态的寿命与核自旋之间的J耦合和化学环境是相关的.在丙烯酸的三个氢原子核自旋体系内, 化学位移相差较大、J耦合较小的两个氢核之间的核自旋单重态占主要成分时, 核自旋单重态的寿命较长; 而当其他核自旋单重态占主要成分时, 整个核自旋单重态的寿命较短.由此也说明在多自旋体系中, 可能存在多种形式的长寿命核自旋单重态, 并且这些核自旋单重态的寿命存在一定的差异.另外, 我们还以丙烯酸样品为例, 研究了长寿命核自旋单重态的寿命对温度的依赖性.

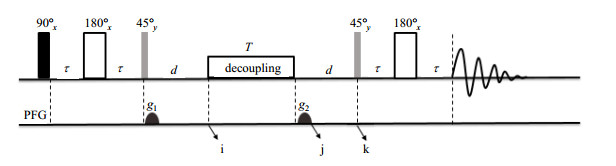
1 理论部分

图 1是产生核自旋单重态的脉冲序列, 其中τ和d分别表示自由演化时间, 实心黑色和空心白色以及实心灰色矩形方框分别表示90°_x、180°_x、45°_y硬脉冲, 右下角下标表示脉冲的相位.g₁和g₂表示沿z方向的梯度脉冲.T表示去耦时间.

该类型的脉冲序列最早由Vasos等人^[5]应用到丙烯酸的核自旋单重态的制备中.相较于文献[5]中的序列, 本文将梯度脉冲g₂由节点k处移至j处.其中从起点到i处表示核自旋单重态的制备过程, i至j表示核自旋单重态的保存阶段, j之后是核自旋单重态的检测阶段.对于一般的孤立三自旋弱耦合体系, 将自旋标记为A、B、C, 其在NMR谱图中对应的化学位移分别记为υ_A、υ_B、υ_C, 核自旋之间的J耦合常数分别记为J_AB、J_AC、J_BC.在热平衡状态下, 积算符形式为:

$ {\rho _{\rm{0}}} = {I_{AZ}} + {I_{BZ}} + {I_{CZ}} $

(1)

经过图 1所示的脉冲序列中的射频脉冲和自由演化哈密顿量的作用, 自旋体系在i处的核自旋对应的积算符记为${\rho _{\rm{i}}}$, 其具体形式在三重态-单重态基矢(STB)空间^[15]中可表示为:

$ {\rho _{\rm{i}}}{\rm{ = }}- \frac{1}{{\sqrt 3 }}\left\{ {\left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \left| {{S_0}} \right\rangle {{\left\langle {{S_0}} \right|}_{AC}} \\ + \left[{\frac{{\sqrt 3 }}{{\rm{4}}} + \frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \left| {{T_0}} \right\rangle } \right.{\left\langle {{T_0}} \right|_{AC}}\\ \left. {{\rm{ }} - \frac{{\sqrt 3 }}{{\rm{4}}}(\left| {{T_{ - 1}}} \right\rangle {{\left\langle {{T_{ - 1}}} \right|}_{AC}} + \left| {{T_{ + 1}}} \right\rangle {{\left\langle {{T_{ + 1}}} \right|}_{AC}})} \right\} \\ \cdot \sin {J_{AC}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AB}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{BC}}{\rm{ \mathsf{ π} }}2\tau )\\ {\rm{ }} - \frac{1}{{\sqrt 3 }}\left\{ {\left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _B}){\rm{ \mathsf{ π} }}d} \right]} \right. \cdot \left| {{S_0}} \right\rangle {\left\langle {{S_0}} \right|_{AB}} \\ + \left[{\frac{{\sqrt 3 }}{{\rm{4}}} + \frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \left| {{T_0}} \right\rangle {\left\langle {{T_0}} \right|_{AB}}\\ {\rm{ }} - \left. {\frac{{\sqrt 3 }}{{\rm{4}}}(\left| {{T_{ - 1}}} \right\rangle {{\left\langle {{T_{ - 1}}} \right|}_{AB}} + \left| {{T_{ + 1}}} \right\rangle {{\left\langle {{T_{ + 1}}} \right|}_{AB}})} \right\} \\ \cdot \sin {J_{AB}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AC}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{BC}}{\rm{ \mathsf{ π} }}2\tau )\\ {\rm{ }} - \frac{1}{{\sqrt 3 }}\left\{ {\left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _B}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right]} \right. \cdot \left| {{S_0}} \right\rangle {\left\langle {{S_0}} \right|_{BC}} \\ + \left[{\frac{{\sqrt 3 }}{{\rm{4}}} + \frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \left| {{T_0}} \right\rangle {\left\langle {{T_0}} \right|_{BC}}\\ {\rm{ }} -\left. {\frac{{\sqrt 3 }}{{\rm{4}}}(\left| {{T_{ -1}}} \right\rangle {{\left\langle {{T_{ -1}}} \right|}_{BC}} + \left| {{T_{ + 1}}} \right\rangle {{\left\langle {{T_{ + 1}}} \right|}_{BC}})} \right\} \\ \cdot \sin {J_{BC}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AB}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{AC}}{\rm{ \mathsf{ π} }}2\tau ) $

(2)

(2) 式中S₀代表单重态, T₀、T_-1和T₊₁代表三重态, 下标A、B、C分别代表三个氢核自旋的标号.接下来应用连续波(CW)去耦脉冲对核自旋单重态进行保存, 其原理是通过匹配合适的去耦功率消除所要制备核自旋单重态的核自旋之间的化学位移差别, 阻止核自旋单重态与核自旋三重态之间的相干转换.在脉冲序列的节点j处, 核自旋对应的积算符记为ρ_j, 其具体形式在STB空间^[15]中可表示为:

$ \begin{array}{l} {\rho _{\rm{j}}}{\rm{ = }} \\ - \frac{1}{{\sqrt 3 }}\left\{ {\left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \left| {{S_0}} \right\rangle {{\left\langle {{S_0}} \right|}_{AC}}} \right\} \cdot \sin {J_{AC}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AB}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{BC}}{\rm{ \mathsf{ π} }}2\tau )\\ {\rm{ }} - \frac{1}{{\sqrt 3 }}\left\{ {\left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _B}){\rm{ \mathsf{ π} }}d} \right] \cdot \left| {{S_0}} \right\rangle {{\left\langle {{S_0}} \right|}_{AB}}} \right\} \cdot \sin {J_{AB}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AC}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{BC}}{\rm{ \mathsf{ π} }}2\tau )\\ {\rm{ }} - \frac{1}{{\sqrt 3 }}\left\{ {\left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _B}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \left| {{S_0}} \right\rangle {{\left\langle {{S_0}} \right|}_{BC}}} \right\} \cdot \sin {J_{BC}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AB}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{AC}}{\rm{ \mathsf{ π} }}2\tau ) \end{array} $

(3)

孤立三自旋体系核自旋单重态的表达形式^[5]:

$ \begin{array}{l} {Q_s} = \frac{1}{{\sqrt 3 }}({\lambda _{AB}}\mathop {{I_A}}\limits^ \rightharpoonup \cdot \mathop {{I_B}}\limits^ \rightharpoonup + {\lambda _{AC}}\mathop {{I_A}}\limits^ \rightharpoonup \cdot \mathop {{I_C}}\limits^ \rightharpoonup + {\lambda _{BC}}\mathop {{I_B}}\limits^ \rightharpoonup \cdot \mathop {{I_C}}\limits^ \rightharpoonup )\\ {\rm{ }} = \frac{1}{{\sqrt 3 }}[{\lambda _{AB}}({I_{AX}}{I_{BX}}{\rm{ + }}{I_{AY}}{I_{BY}} + {I_{AZ}}{I_{BZ}}) + \\ {\lambda _{AC}}({I_{AX}}{I_{CX}}{\rm{ + }}{I_{AY}}{I_{CY}} + {I_{AZ}}{I_{CZ}}) + {\lambda _{BC}}({I_{BX}}{I_{CX}}{\rm{ + }}{I_{BY}}{I_{CY}} + {I_{BZ}}{I_{CZ}})] \end{array} $

(4)

其中${\lambda _{AB}}$、${\lambda _{AC}}$、${\lambda _{BC}}$分别表示核自旋A和B、核自旋A和C、核自旋B和C组合成的核自旋单重态对应的系数.通过(3)式与(4)式的进一步计算可得到系数${\lambda _{AB}}$、${\lambda _{AC}}$、${\lambda _{BC}}$的表达式:

$ \begin{array}{l} {\lambda _{AC}} \equiv \left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \sin {J_{AC}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AB}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{BC}}{\rm{ \mathsf{ π} }}2\tau )\\ {\lambda _{AB}} \equiv \left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _A}-{\upsilon _B}){\rm{ \mathsf{ π} }}d} \right] \cdot \sin {J_{AB}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AC}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{BC}}{\rm{ \mathsf{ π} }}2\tau )\\ {\lambda _{BC}} \equiv \left[{\frac{{\sqrt 3 }}{{\rm{4}}}-\frac{{\sqrt 3 }}{4}\cos 2({\upsilon _B}-{\upsilon _C}){\rm{ \mathsf{ π} }}d} \right] \cdot \sin {J_{BC}}{\rm{ \mathsf{ π} }}2\tau (\cos {J_{AB}}{\rm{ \mathsf{ π} }}2\tau + \cos {J_{AC}}{\rm{ \mathsf{ π} }}2\tau ) \end{array} $

(5)

其中${\lambda _{AB}}$、${\lambda _{AC}}$、${\lambda _{BC}}$满足归一化与耦合方程^[5]:

$ \begin{array}{l} {\lambda _{AB}}^2 + {\lambda _{AC}}^2 + {\lambda _{BC}}^2 = 1\\ {\lambda _{AB}}({J_{AC}}-{J_{BC}}) + {\lambda _{BC}}({J_{AB}}-{J_{AC}}) = {\lambda _{AC}}({J_{AB}}-{J_{BC}}) \end{array} $

(6)

在已知核自旋之间的J耦合和化学位移参数的基础上, 上述方程组可用Fortran语言编程求解, 得到制备孤立三自旋弱耦合体系核自旋单重态需要的参数τ和d, 以及相应的系数${\lambda _{AB}}$、${\lambda _{AC}}$、${\lambda _{BC}}$.以丙烯酸氢核自旋体系为例, 通过计算得到了多组满足方程(6)的解, 在理论计算中没有考虑信号驰豫效应, 但在实际体系中, 信号在自由演化期间会随着驰豫时间增加而衰减, 在此为了最大化的降低驰豫带来的信号衰减影响, 在演化时间(2τ+ d)取最小值的限制条件下筛选出了核自旋A和B, 核自旋A和C单重态分别占有比例系数最大时的两组解:

$ \begin{array}{l} \tau = 109.10\;{\rm{ms, }}\;d = 1.91\;{\rm{ms, }} \;{\lambda _{AB}} =-0.31{\rm{, }}\;{\lambda _{AC}} =-0.92{\rm{, }}\;{\lambda _{BC}} = 0.21;\\ \tau = 17.80\;{\rm{ms, }}\;d = 5.28\;{\rm{ms, }}\;{\lambda _{AB}} = 0.87{\rm{, }}\;{\lambda _{AC}} = 0.0006{\rm{, }}\;{\lambda _{BC}} = 0.49. \end{array} $

同样地, 对于多巴胺氢自旋体系中核自旋单重态的制备需要的参数和自旋单重态的成分比例系数为:

$ \begin{array}{l} \tau = 14.30\;{\rm{ms, }}\;d = 8.44\;{\rm{ms, }}\;{\lambda _{AB}} = 0.04{\rm{, }}\;{\lambda _{AC}} = 0.98{\rm{, }}\;{\lambda _{BC}} = 0.22;\\ \tau = 670.00\;{\rm{ms, }}\;d = 16.91\;{\rm{ms, }}\;{\lambda _{AB}} =-0.77{\rm{, }}\;{\lambda _{AC}} =-0.03{\rm{, }}\;{\lambda _{BC}} =-0.64. \end{array} $

2 实验部分 2.1 仪器与试剂

仪器:AVANCE III 500 NMR谱仪(Bruker)、Shigemi NMR样品管.

试剂:丙烯酸(Aldrich)、重水(D₂O, 青岛腾龙科技有限公司).

2.2 实验过程 2.2.1 试样准备

配制丙烯酸的D₂O溶液, 其中丙烯酸的体积分数为13%.

2.2.2 NMR实验

丙烯酸的分子式为C₃H₄O₂, 三个质子分别标记为A、B、C.在温度25 ℃时, 采用zg脉冲序列(d1-90°-ACQ)得到了静态¹H NMR谱, 通过反转恢复法测得的三个质子的T₁分别为(4.12±0.02)s、(9.17±0.15)s、(3.22±0.02)s.

2.2.3 长寿命核自旋单重态的NMR制备实验

在制备的核自旋单重态中质子对AB占有比例系数最大时, ¹H核的观测频率为(υ_A+υ_B)/2 MHz, 在制备的核自旋单重态中质子对AC占有比例系数最大时, ¹H核的观测频率为(υ_A+υ_C)/2 MHz, 其中υ_A、υ_B、υ_C分别为自旋A、B、C的化学位移.出于对样品化学性质的考虑, 变温实验采样温度分别设置为15 ℃、25 ℃、35 ℃和45 ℃, 采用图 1所示的脉冲序列进行长寿命核自旋单重态的NMR制备实验, 具体参数如下:丙烯酸溶液采样谱宽(SW)为5 000 Hz, 实验所用90°、180°、45°硬脉冲脉宽分别为10 μs、20 μs、5 μs.梯度脉冲g₁和g₂的脉冲宽度分别为(1 000 μs, 40%)、(800 μs, 70%), 实验所用的去耦(decoupling)方式为CW去耦, 去耦功率为0.063 W, 累加次数(NS)为1.

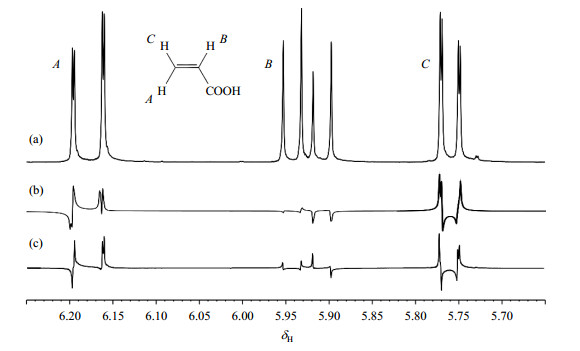
3 结果与讨论 3.1 丙烯酸长寿命核自旋单重态的模拟与NMR实验

图 2(a)所示为25 ℃下, 丙烯酸的D₂O溶液在500 MHz(B₀ = 11.75 T)的静态¹H NMR谱, 从左至右分别是丙烯酸三个质子的信号, 分别标记为A, B, C.通过谱图分析可知它的J耦合参数和化学位移参数为:

$ \begin{array}{l} {J_{AB}} = 17.{\rm{3 Hz, }}\;{J_{AC}} = 1.{\rm{4 Hz, }}\;{J_{BC}} = 10.{\rm{4 Hz}};\\ \left| {{\upsilon _A}-{\upsilon _C}} \right| = 21{\rm{2 Hz, }}\;\left| {{\upsilon _A}-{\upsilon _B}} \right| = {\rm{124 Hz, }}\;\left| {{\upsilon _B}-{\upsilon _C}} \right| = {\rm{88 Hz}} \end{array} $

在此基础上, 我们选择一组实验参数:τ= 109.10 ms, d = 1.91 ms, 运用图 1所示的脉冲序列进行计算, 假设梯度脉冲g₂能完全去除连续波带来的噪声影响, 图 1中k点处的理论积算符${\rho _{\rm{k}}}$为:

$ \begin{array}{l} {\rho _{\rm{k}}}{\rm{ = }}-0.179({I_{AX}}{I_{BX}} + {I_{AY}}{I_{BY}} + {I_{AZ}}{I_{BZ}})-0.{\rm{53}}({I_{AX}}{I_{CX}} + {I_{AY}}{I_{CY}} + {I_{AZ}}{I_{CZ}})\\ {\rm{ }} + 0.12({I_{BX}}{I_{CX}} + {I_{BY}}{I_{CY}} + {I_{BZ}}{I_{CZ}}) \end{array} $

在节点k之后的后续检测脉冲作用下得到了图 2(b)所示的脉冲的理论模拟谱图, 模拟谱图由Simpson程序得到.图 2(c)表示在上述实验参数下, CW去耦时间(T)为13 s时得到的核自旋单重态的实验谱图, 其成分比例为${\lambda _{AB}} =-0.31$、${\lambda _{AC}} =-0.92$、${\lambda _{BC}} = 0.21$, 即在其核自旋单重态中质子对AC所占有的比例系数最大.通过对比可知, 实验检测的核自旋单重态信号与理论计算模拟相符合, 这说明本实验所使用的连续波去耦和梯度脉冲实现了对核自旋单重态的保存和过滤.同样地, 运用另一组演化时间$\tau = 17.80$ ms、$d = 5.28$ ms, 实验制备了系数分配为${\lambda _{AB}} = 0.87$、${\lambda _{AC}} = 0.000\;6$、${\lambda _{BC}} = 0.49$的长寿命核自旋单重态, 在这样一组核自旋单重态中, 核自旋AB的比例成分最大.

3.2 丙烯酸长寿命核自旋单重态的寿命探测

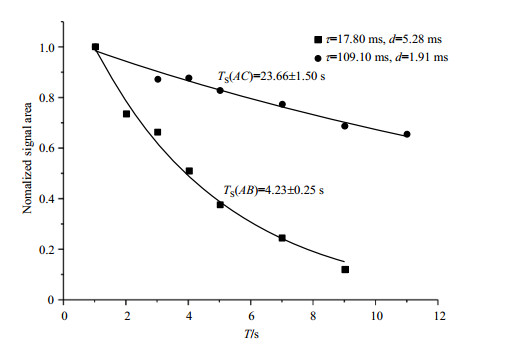
长寿命核自旋单重态的主要特点是其NMR谱峰信号强度衰减常数T_S大于T₁.在图 2的基础上, 实验中通过改变CW去耦时间T, 采集到了一系列谱图, 通过单指数拟合可得到长寿命核自旋单重态的寿命T_S.图 3是实验制备的两组核自旋单重态的T_S拟合图, 其中由参数t = 17.80 ms、d = 5.28 ms, 制备的成分比例为${\lambda _{AB}} = 0.87$、${\lambda _{AC}} = 0.000\;6$、${\lambda _{BC}} = 0.49$的核自旋单重态的T_S为(4.23±0.25)s, 是T₁的1.02倍.而由参数τ= 109.10 ms、d = 1.91 ms制备的成分为${\lambda _{AB}} =-0.31$、${\lambda _{AC}} =-0.92$、${\lambda _{BC}} = 0.21$的核自旋单重态的T_S为(23.66±1.50)s, 是T₁的5.74倍, 比样品中质子具有的最长T₁增长了2.58倍.由此可见, 在丙烯酸的三个氢原子核体系内, 不同比例系数组合的长寿命单重态的T_S是不同的, 化学位移相隔较远的两个氢原子核之间的J耦合比较小, 并且分别与第三个氢原子核的J耦合较大, 当它们之间的长寿命单重态占有的成分较大时, 核自旋单重态的T_S较长.其余两对化学位移相离较近的两个氢原子核之间的核自旋单重态所占的成分较大时, 整个核自旋单重态的T_S较短.这一方面说明三自旋体系中核自旋单重态的组合系数形式不同时, 对应态的寿命不同; 同时也暗示丙烯酸分子中亚甲基上的两个氢原子核之间能产生寿命较长的长寿命单重态.在下一步的工作中, 我们将设计脉冲序列, 用于产生单纯的两个氢之间的长寿命单重态, 并对其T_S进行实验探测.

3.3 丙烯酸核自旋单重态寿命与温度的关系探究

为了进一步探究丙烯酸长寿命核自旋单重态的T_S受温度变化的影响, 特别是长寿命核自旋单重态寿命相比纵向弛豫时间增加的倍数(T_S/T₁)与温度的关系, 实验中改变样品温度, 得到了表 1所示的实验结果, 表中数据的误差由数据拟合过程给出.由结果可以看出随着温度的增加, T₁、T_S值都增加; 相反的, T_S(AC)/T₁(B)值随温度增加而降低.这说明随着温度的增加, T₁增加的幅度要比T_S增加的幅度大.对于T₁随着温度的增加而增加, 从分子运动相关的弛豫机制来理解, 即在丙烯酸溶液体系所在的高频率运动范围内, 随着温度增加, 分子运动加快, 分子运动相关时间减小, 最终T₁增加.而核自旋单重态寿命T_S随温度的变化与T₁的不同应该是两种核自旋态存在不同的弛豫机制所导致的.

4 结论

本文以孤立三自旋弱耦合体系为研究对象, 给出了适用于任何三自旋弱耦合体系制备长寿命核自旋单重态的参数计算方法.以丙烯酸和多巴胺样品为例, 得到在各自自旋体系中, 制备核自旋单重态的参数以及任意两氢核自旋之间组合的单重态占有的比例系数.

本文对丙烯酸进行了长寿命核自旋单重态的实验制备, 得到了两组不同系数组合的核自旋单重态, 并发现不同的比例系数组合成的单重态的寿命T_S不同, 为了更深入地探索决定其寿命的机制, 我们在下一步的工作中将制备单纯的两两自旋之间的单重态, 比较这些单重态寿命的区别以及与本文中组合态的关联, 以便理解分子构型与其内部的弛豫机制.另外, 通过变温实验, 本文探究了丙烯酸体系中氢核的核自旋单重态的寿命T_S随温度的变化规律, 由于弛豫机制的不同, 随温度的增加, T_S相比T₁增加的更慢.