2. 重庆师范大学 物理与电子工程学院, 重庆 401331
2. College of Physics and Electronics Engineering, Chongqing Normal University, Chongqing 401331, China
射频脉冲激励是核磁共振(NMR)信号产生的先决条件,对射频脉冲信号幅度、频率、相位、波形和持续时间等参数的精确控制,不仅显著影响NMR检测结果和磁共振图像质量,也可以通过合理的序列设计,进一步拓展NMR的应用范围.其中,射频脉冲的频率控制应与静磁场中质子系统的拉莫尔频率保持一致,这是确保NMR信号产生的关键;射频脉冲的相位控制已经发展成为一套相位循环技术,这对于伪信号的消除及相干路径的选择具有重要意义[1];在一定的射频脉冲持续时间下,射频脉冲的幅度控制可以灵活实现各种角度的磁化矢量翻转,这被广泛应用于快速磁共振成像(MRI)技术的研究.此外,选择性激发在NMR研究诸多方面也越来越重要,例如选择性观测、溶剂峰抑制、多维谱分析、MRI等都离不开选择性激发[2],而实现选择性激发的本质在于通过对射频脉冲进行包络整形实现带宽设计,即射频软脉冲的实现.
产生射频脉冲信号的硬件设备称为射频脉冲发生器.目前,射频脉冲发生器的设计多采用以下两种结构:(1)采用现场可编程门阵列(FPGA)驱动直接数字频率合成(DDS)芯片或集成DDS内核的方式生成一定幅度的基频信号,同时通过读取随机存取存储器(RAM)中波形调制数据生成包络信号,二者分别经数模(DA)转换后通过模拟乘法器相乘实现波形调制[3-6];(2)采用FPGA集成DDS内核的方式生成基频信号和包络信号后,首先在FPGA内部经数字乘法器进行波形调制,再经DA转换输出所需射频脉冲[7, 8].前者采用模拟调制技术,开发难度较小,但硬件成本较高,且引入了过多的模拟器件,抗干扰能力差;后者采用数字调制技术,增强了抗干扰能力,降低了硬件成本,但其在完成数字化的波形调制后,对射频脉冲总体幅度的控制是通过调节DA转换器的参考电平实现的,是一种不完全的数字调制技术.
基于上述原因,本文基于集成了并行接口和DA转换的高速DDS芯片,提出了一种更为简易的射频脉冲发生器解决方案,通过FPGA直接驱动DDS的方式对射频脉冲的各项参数进行完全的数字化并行调制,将波形调制的时间分辨率降低至10 ns,可灵活生成短至0.1 μs的任意可编程射频脉冲信号.
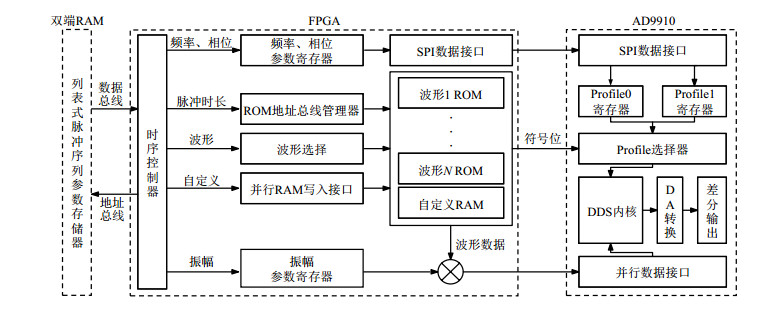
1 结构与方法 1.1 系统结构本文提出的射频脉冲发生器由FPGA(EP4CE15F17C8)和DDS芯片(AD9910)组成,其硬件结构框图如图 1所示.
|
图 1 射频脉冲发生器结构框图 Figure 1 Block diagram of RF pulse generator |
AD9910是一款高性能DDS芯片,内部运行时钟为1 GHz,支持高达400 MHz的模拟输出,其频率、相位、幅度的分辨率分别为32位、16位和14位,支持单频、并口、RAM和数字斜坡发生器(DRG)四种调制模式,可灵活实现多种调制功能.内置的一个1 GSPS(每秒千兆次采样)14位数模转换器(DAC),使射频脉冲发生器在硬件上节约了一个外置DAC芯片,支持两路平衡输出,可有效抑制信号传输中的共模噪声.本文采用单频模式控制频率、相位及并口模式控制幅度的方法进行射频脉冲的调制.在单频模式中,DDS的信号控制参数由Profile寄存器直接提供,通过串行外设接口(SPI)将不同频率、相位及幅度的参数分别写入不同的Profile寄存器,结合外部引脚的Profile选择功能,可实现最多8种射频参数的快速切换;在并口模式中,DDS信号控制参数由18位高速并行端口(2位目的字和16位数据字)直接提供,数据采样率可达250 MHz.
FPGA根据序列参数要求控制AD9910的输出,运行时钟为100 MHz.SPI负责AD9910相关寄存器的数据写入,主要用于AD9910配置文件及射频脉冲频率、相位参数的调整.多个1 024×12位波形存储器用于存储-1~1之间分辨率为2-10的波形系数文件,其11数据位的数据在数字乘法器作用下与14位的振幅参数共同生成14位的波形调制数据,经并行数据接口对射频输出进行实时调制,调制的时间精度为10 ns;其1符号位数据控制Profile寄存器的切换,类似于乒乓操作,通过在两个Profile寄存器分别写入互为反相的射频参数,即可实现波形调制过程中的快速反相处理.
1.2 参数调制射频脉冲的主要调制参数包括幅度、相位、频率、时长和波形等.
(1)频率参数在一个射频脉冲发生过程中不发生变化,在射频脉冲发生前将频率参数通过SPI写入Profile寄存器的32频率位即可完成频率参数的数字调制.
(2)对于硬脉冲而言,相位参数在射频脉冲发生过程中不会改变,但软脉冲的包络波形在过零点处存在反相问题.考虑到SPI无法满足此类反相操作对速度的要求,采用乒乓操作的思想,通过在两个Profile寄存器中写入互为反相的相位参数,利用波形数据的符号位控制Profile寄存器的快速切换选择,从而完成调制过程中的快速反相操作.
(3)可选包络波形存储于波形只读存储器(ROM)中,波形数据是范围在-1~1之间的12位有符号型乘法系数,其1符号位用于控制Profile寄存器的切换,其11数据位与14位振幅参数做数字乘法运算后实时生成14位的幅度数据输出到AD9910的并行调制接口,完成对输出射频脉冲幅度的实时数字调制.
(4)由于波形文件为固定的1 024×12位数据,FPGA运行时钟固定在100 MHz,故针对不同脉冲时长应对ROM的读取速率做出相应的调整,此部分任务由ROM地址总线管理器实现:针对大于10.24 μs的射频脉冲通过调整ROM地址步进的时间间隔来进行脉冲时长匹配,针对小于10.24 μs的射频脉冲通过调整ROM地址的步进间隔来进行脉冲时长匹配.
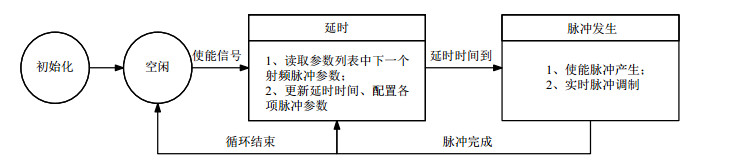
1.3 时序控制射频脉冲各项参数的时序配合是通过FPGA内部的时序控制器来完成的,控制过程如图 2所示.按照一定的格式,上级控制单元将射频脉冲参数以脉冲发生的先后顺序写入双端口RAM中,形成一个脉冲参数检索表,射频脉冲发生器按照以下步骤完成射频脉冲序列的产生.
|
图 2 射频脉冲发生器控制流程图 Figure 2 Control flow diagram of RF pulse generator |
(1)初始化:硬件在上电或复位后先通过初始化阶段完成对AD9910的基础配置,主要包括AD9910的运行时钟、调制模式等功能寄存器的参数更新,与此同时,完成AD9910和FPGA各模块的初始化.
(2)空闲:完成各模块初始化配置后,等待上级控制单元的使能信号.
(3)延时:令双端口RAM的地址加1,读取下一个射频脉冲的调制参数,更新本阶段的延时时间,完成波形存储器的选择,并通过SPI将频率、相位信息写入相应的Profile寄存器,当延时时间到时执行下一步骤.
(4)脉冲发生:ROM地址总线管理器根据脉冲时长调整地址步进率,在脉冲发生期间均匀读取波形系数文件,与振幅数据做乘法运算后生成14位并行调制数据后按100 MHz的速率对射频信号进行实时调制,同时波形文件的符号位通过控制Profile寄存器的切换进行快速反相处理.当射频脉冲完成后,执行步骤(3),若整个序列已经完成,则执行步骤(2).
上述时序控制单元将射频脉冲序列简化为一系列“脉冲+延时”基本单元的组合,将复杂多样的脉冲序列参数化、列表化,通过一个双端口RAM即可完成各类脉冲序列的生成,接口简单,具有较高的灵活性.
1.4 频谱优化 1.4.1 射频调制的频谱特性NMR射频信号的波形调制是为了得到更好的频谱特性.设载波信号为
| $ F(\omega ) = F\left[ {\cos ({\omega _0}t) \cdot G(\omega )} \right] = F\left[ {\frac{1}{2}({{\rm{e}}^{j{\omega _0}t}} + {{\rm{e}}^{ - j{\omega _0}t}}) \cdot G(\omega )} \right] = \frac{1}{2}G(\omega + {\omega _0}) + \frac{1}{2}G(\omega - {\omega _0}) $ | (1) |
可以看出,调制后的射频脉冲信号频谱是调制信号频谱左右平移
|
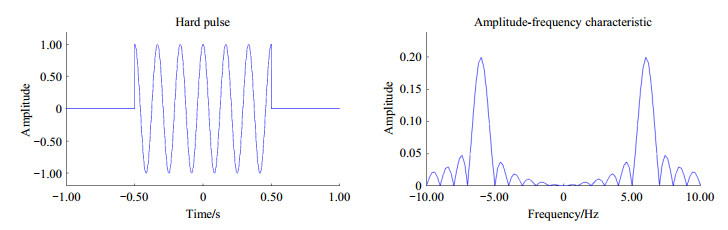
图 3 硬脉冲波形及其频谱示意图 Figure 3 Schematic diagram of waveform and spectrum of the hard pulse |
显然,硬脉冲的频谱按照矩形窗函数的频谱形状向两侧扩散,呈现出比较严重的频率泄漏现象[9],这对选择激励有着非常不利的影响.考虑到Sinc函数的频谱为矩形窗,因此,实际应用中常常选用Sinc函数进行波形调制以实现更好的频带选择功能,这种脉冲被称为软脉冲,图 4给出了理想情况下采用无限长Sinc函数对载波信号进行调制的结果.

|
图 4 理想情况下的软脉冲波形及频谱示意图 Figure 4 Schematic diagram of waveform and spectrum of the idea soft pulse |
理想的Sinc函数在时域上是一个无限延伸的信号,其对应频谱为矩形窗,具有优异的频带选择性能.但受射频脉冲时间限制,软脉冲信号一般只截取部分Sinc函数作为调制波形[9],这种截断等效于对Sinc函数在时域设置了矩形窗,这将引起Sinc函数的频谱泄漏,从而无法得到理想的带通性能,为了减少这种畸变,通常改用Hanning窗进行Sinc函数的截取.Hanning窗频谱的第一旁瓣最大衰减为-42 dB,远隔旁瓣按照-2 dB/个的速度下降[10],可以很好的抑制频谱的旁瓣泄漏.
通过对Sinc函数施加Hanning窗得到的调制波形为:
| $ K(t) = \left[ {0.{\rm{46}} + 0.5{\rm{4}}\cos (\frac{{{\rm{ \mathsf{ π} }}t/{t_0}}}{N})} \right]\frac{{\sin ({\rm{ \mathsf{ π} }}t/{t_0})}}{{{\rm{ \mathsf{ π} }}t/{t_0}}} $ | (2) |
(2) 式中

|
图 5 采用矩形窗和Hanning窗的调制效果对比图. (a)单瓣截断;(b)三瓣截断;(c)五瓣截断 Figure 5 Modulation effects of the rectangular window and Hanning window. (a) 1-lobe truncation; (b) 3-lobe truncation; (c) 5-lobe truncation |
FPGA和AD9910采用50 MHz时钟输入,分别经内部锁相环(PLL)倍频至100 MHz和1 GHz作为运行时钟.射频脉冲发生器所产生的射频信号采用Tektronix-MDO4034B-3示波器进行测量.
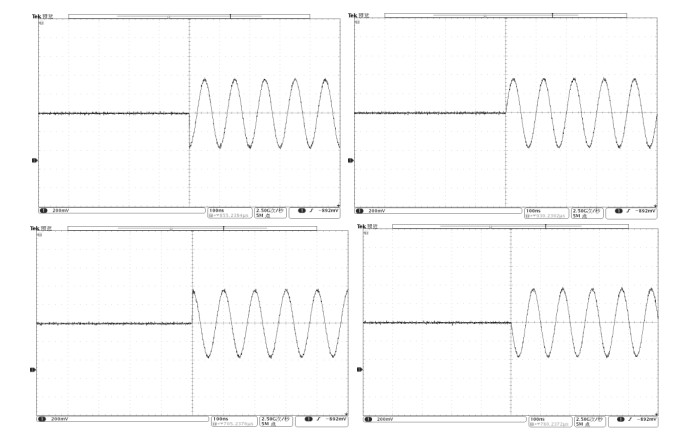
为更好的观察射频脉冲发生器总体振幅和脉冲时间的控制效果,我们对100 MHz的硬脉冲信号进行了测试,测试结果如图 6(a)所示.从左到右的四个脉冲的设计脉冲时长分别是40 μs、20 μs、10 μs、5 μs,设计振幅分别是满振幅、3/4振幅、1/2振幅、1/4振幅,从图中可以看出,输出脉冲时长和振幅均符合要求.为了进一步验证脉冲时长的控制精度,对0.1 μs的射频脉冲进行了测试,其脉冲频率为100 MHz,测试结果如图 6(b)显示,脉冲时间长度为9.5个周期,即0.095 μs,与0.1 μs设计脉冲时长相差仅0.005 μs,该误差小于系统最小运行时钟0.01 μs,故该射频脉冲发生器可以保证0.01μs以下的时间精度.

|
图 6 (a) 脉冲序列的时间及幅度控制效果图;(b) 0.1 μs硬脉冲,时间精度为0.01 μs Figure 6 (a) The time and amplitude control effect of pulse sequence; (b) 0.1 μs hard pulse, time precision is 0.01 μs |
为了验证相位调节的有效性,设计产生了四个初始相位依次增加π/4的射频脉冲,如图 7所示,结果表明,其相位调制性能良好.
|
图 7 四种初始相位依次增加π/4的硬脉冲相位调制 Figure 7 Phase modulation for four hard pulses with initial phases increasing π/4 in an order |
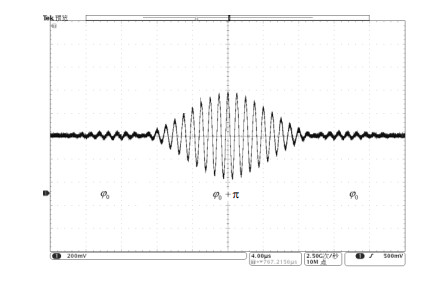
此外,为了观察软脉冲波形调制过程中的反相处理结果,我们生成了一个载波频率为1 MHz的三瓣Sinc型软脉冲,如图 8所示.根据Sinc函数特性,生成的射频软脉冲应在其包络线的每次过零点处进行反相处理,即相邻波瓣的相位相反,从图 8可以看出,射频信号在主瓣和副瓣中达到了预期的反相效果.
|
图 8 三瓣Sinc型软脉冲波形调制.主瓣和副瓣中的射频信号相位相反 Figure 8 Waveform modulation for the 3-lobe-Sinc soft pulse with opposite phase in the main lobe and the sub-lobe |
射频软脉冲的频谱性能是判断其质量的重要指标,为验证频谱优化效果,本文采用Keysight-N9000B信号分析仪分别对采用矩形窗和Hanning窗得到的Sinc型射频软脉冲进行了频谱测试,为了便于分析对比,三种不同瓣数的软脉冲均设计为t0=10 μs,即理想情况下频谱带宽为

|
图 9 单瓣Sinc型软脉冲. (a)矩形窗,波形;(b) Hanning窗,波形;(c)矩形窗,频谱;(d) Hanning窗,频谱 Figure 9 1-lobe-Sinc soft pulse. (a) Rectangular window, waveform; (b) Hanning window, waveform; (c) Rectangular window, frequency spectrum; (d) Hanning window, frequency spectrum |
|
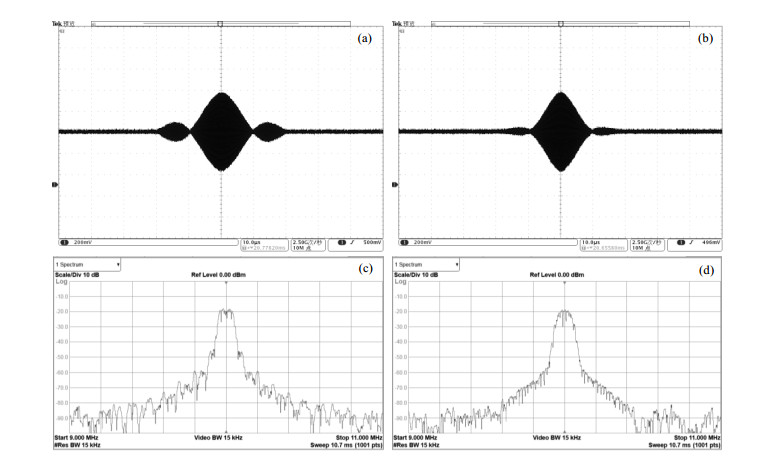
图 10 三瓣Sinc型软脉冲. (a)矩形窗,波形;(b) Hanning窗,波形;(c)矩形窗,频谱;(d) Hanning窗,频谱 Figure 10 3-lobe-Sinc soft pulse (a) Rectangular window, waveform; (b) Hanning window, waveform; (c) Rectangular window, frequency spectrum; (d) Hanning window, frequency spectrum |
|
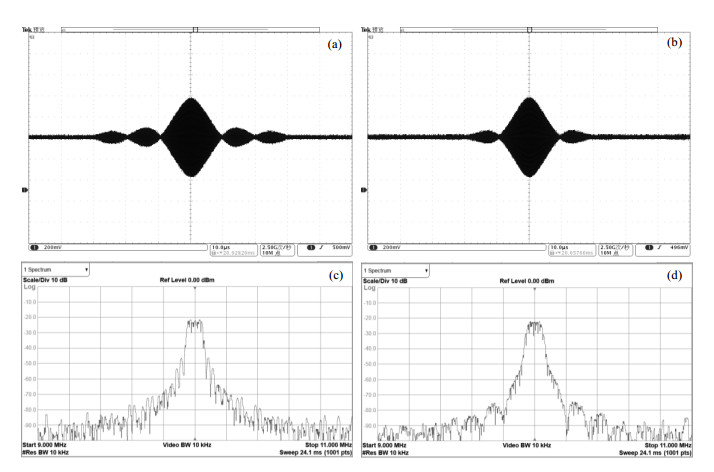
图 11 五瓣Sinc型软脉冲. (a)矩形窗,波形;(b) Hanning窗,波形;(c)矩形窗,频谱;(d) Hanning窗,频谱 Figure 11 5-lobe-Sinc soft pulse (a) Rectangular window, waveform; (b) Hanning window, waveform; (c) Rectangular window, frequency spectrum; (d) Hanning window, frequency spectrum |
可以看出,在射频脉冲的波形上,经Hanning窗得到的脉冲包络在边缘处衰减更加明显,这与仿真结果一致.在射频脉冲的频谱上,采用Hanning窗可以有效抑制副瓣频谱的高度,增强了频带选通性能.需要说明的是,在五瓣Sinc型软脉冲上,由于边缘波瓣振幅过小,难以在示波器上检测到.
3 结论本文基于数字调制技术,采用FPGA直接驱动AD9910芯片的方式,设计了一种结构简单、控制灵活的数字化射频脉冲发生器,测试结果表明,各项参数达到设计要求,实现了0.01 μs的射频脉冲调制精度;通过提取脉冲序列的“脉冲+延时”基本模型,在FPGA内部集成了序列控制单元,对上级控制单元实现了列表式脉冲序列参数编写方案,简化了系统开发及拓展的难度;针对Sinc型软脉冲,通过Hanning窗对其频谱进行了优化,获得了更好的频带选择性能.下一步研究中,将继续完成信号接收器、梯度控制器等其他模块的开发工作,以实现更加完备的数字化谱仪系统.
| [1] |
GAO H B, ZHOU J Y, WU Q Y. Equivalence theorem in phase loop design and impulse unit method[J].
Chinese J Magn Reson, 1991, 8(4): 447-454.
高汉宾, 周进元, 吴钦义. 相位循环设计中的等价性定理和脉冲单元法[J]. 波谱学杂志, 1991, 8(4): 447-454. |
| [2] |
LI G Y, XIE H B. The development of universal NMR soft pulse unit[J].
Chinese J Magn Reson, 1998, 15(6): 551-556.
李鲠颖, 谢海滨. 通用的NMR软脉冲单元研制[J]. 波谱学杂志, 1998, 15(6): 551-556. |
| [3] | XIAO L, WANG W M. A radio-frequency source using direct digital synthesis and field programmable gate array for nuclear magnetic resonance[J]. Rev Sci Instrum, 2009, 80(12): 124703. DOI: 10.1063/1.3271379. |
| [4] | XIAO L, SUN B H, MA Y P, et al. A digital magnetic resonance imaging spectrometer using digital signal processor and field programmable gate array[J]. Rev Sci Instrum, 2013, 84(5): 054702. DOI: 10.1063/1.4803007. |
| [5] |
LI Y W, XIAO L. A radio frequency pulse generator for magnetic resonance imaging based on FPGA and DDS[J].
Chinese J Magn Reson, 2016, 33(4): 590-596.
李聿为, 肖亮. 基于FPGA与DDS的磁共振成像射频脉冲发生器[J]. 波谱学杂志, 2016, 33(4): 590-596. |
| [6] | TAKEDA K. OPENCORE NMR:open-source core modules for implementing an integrated FPGA-based NMR spectrometer[J]. J Magn Reson, 2008, 192(2): 218-229. DOI: 10.1016/j.jmr.2008.02.019. |
| [7] | TANG W N, WANG W M. A single-board NMR spectrometer based on a software defined radio architecture[J]. Meas Sci Technol, 2011, 22(1): 015902. DOI: 10.1088/0957-0233/22/1/015902. |
| [8] |
HE G, WANG W M. A multi-channel radiofrequency transmitter for high-field MRI[J].
Chinese J Magn Reson, 2017, 34(3): 338-346.
何刚, 王为民. 一种用于高场MRI的多源射频发射机[J]. 波谱学杂志, 2017, 34(3): 338-346. |
| [9] | BERNSTEIN M A, KING K F, ZHOU X H J. Handbook of MRI pulse sequences[M]. Academic Press, 2004, 1452-1452. |
| [10] |
LI H S, CHEN D. Research of the window functions in frequency analysis[J].
Microcomputer Information, 2008, 24(10): 278-279.
李杭生, 陈丹. 频谱分析中窗函数的研究[J]. 微计算机信息, 2008, 24(10): 278-279. |
 2018, Vol. 35
2018, Vol. 35 
