2. 中国科学院大学, 北京 100049;
3. 上海联影医疗科技有限公司, 上海 201807
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shanghai United Imaging Healthcare Cooperation, Shanghai 201807, China
磁共振成像(MRI)技术无电离辐射,能提供多对比度、任意角度的图像,在临床扫描中有着广泛的使用.各种不同采集方法的开发满足了临床上MRI扫描的各种实际需求.例如3D SOS(Stack of Star)径向扫描[1]可以有效降低人体呼吸运动对于MRI扫描的影响,减弱运动伪影,因此得到广泛应用;又如基于压缩感知技术(CS)[2]的3D动态成像使得MRI扫描时间大大缩短.然而这些技术在发挥效用的同时极大地增加了计算复杂性与重建难度,这点在数据量较大的3D磁共振图像重建中体现得尤为明显.
3D磁共振图像重建中,复杂的算法运算极易耗尽计算机内存,而且在重建多个片层图像过程中,基于中央处理器(CPU)的运算会因为CPU本身在并行计算上的性能劣势而耗费过多时间.磁共振设备生产商解决该问题的方法是研发专业的处理器,该类处理器与家用计算机最大的区别通常在于CPU的数量以及内存的大小,例如50核CPU、64 GB以上的内存对于专业处理器是很常见的配置.但它在带来高性能的同时,也增加了成本开销,而且随着重建算法复杂度的不断增加,也会达到该设备的处理上限.
2015年,Xue等人基于Gadgetron[3]平台提出了磁共振云计算重建技术[4],该技术利用网络将数据传输给云端的硬件设备进行计算,使运算突破了计算资源的限制,但也带来了网络传输时间成本与购买云服务的额外开支.Gadgetron平台为美国国立卫生研究院(NIH)近年来开发的开源图像重建软件框架,经过数据格式转换后,Gadgetron平台可以识别多家主流商业MRI设备的扫描数据,从而使重建算法的研发能跨硬件平台实现,显著提升了研究效率.
分析重建算法的实现过程可以发现:复杂算法应用到3D数据的困难源于需要重建多个片层,考虑到在大多数情况下,不同片层的重建相互独立,可以采用分布式并行重建的设计解决该问题,具体方案为搭建包含多块图形处理器(GPU)的计算系统进行异构计算,异构计算[5]属于特殊的分布式并行计算,它将不同的计算任务交给不同构架的机器处理,可以有效发挥不同构架的机器性能特点,从而高效并行地进行图像重建.在此之前,已有研究者利用GPU实现了磁共振图像重建加速,但仅限于单GPU加速特定类型的2D算法[6](能够被加速的2D算法中必须有相互独立的计算步骤以符合GPU并行计算的前提要求).本文将介绍的多GPU分布式重建方法主要用于加速大数据量的3D图像重建,实则将GPU并行计算对于重建性能的提升推广到更广泛的临床与科研应用场景中.多GPU分布式重建过程中并非所有计算步骤都需要GPU并行完成,CPU仍然参与部分计算, 具体负责数据通信、逻辑计算等工作,而将重建算法进行分割之后,把其中运算费时、消耗大量计算资源但相互独立的任务提取出来分配给不同GPU进行并行运算.因为CPU与GPU进行运算时使用不同的数据储存空间,从而减小了许多计算机内存的负担,同时也发挥了CPU适合处理少量复杂任务,GPU适合并行计算大量相对简单任务[7]的性能特点.
本文介绍了3D磁共振图像重建的GPU并行程序设计以及支配多GPU协同工作的方法,之后将分别利用CPU与多GPU分布式方法执行3D SOS图像重建算法,对比两者的重建时间,分析实验结果以展示利用多GPU分布式重建方法的优势.
1 实验部分 1.1 实验系统的搭建实验系统包括软件平台与硬件平台两部分,软件平台需要能识别MRI扫描的原始数据以支持重建算法的开发,硬件平台包括MRI系统和多GPU重建服务器.
1.1.1 实验系统的软件平台——GadgetronGadgetron采用模块化设计,将重建算法的各个步骤进行封装,称为Gadget.Gadgetron是多线程模式的并行程序,能一定程度上提升算法执行的效率.利用Gadgetron进行重建时,磁共振原始数据与重建算法不必置于同一台计算机中,储存磁共振原始数据的计算机与Gadgetron重建服务器通过传输控制/网络通讯协定(TCP/IP)进行通信[8],当用户向Gadgetron发出重建请求后,Gadgetron调用用户指定的重建算法进行图像重建后将重建结果传回.其工作流程如图 1所示.

|
图 1 Gadgetron工作流程:每个Gadget启动一个线程,通过内存缓冲通信 Figure 1 Gadgetron work flow: each Gadget starts a thread, and the threads communicate by memory buffer |
多GPU计算系统硬件组成如下:主要并行计算核心为两块NIVIDIA GeForce GTX 1080 Ti GPU,单块GPU显存为11 GB,计算能力(compute capability)[9]为6.1;CPU选用8核Intel i7-3820 3.60 GHz处理器;内存为24 GB;配有高速网卡;所有硬件置于统一机箱内,利用高速串行计算机扩展总线(PCI-E)进行通信.
MRI系统为上海联影uMR 780 3.0 T MRI系统,包括扫描装置与一台接收扫描所得数据的计算机.整个扫描到重建过程如图 2所示:MRI扫描完成后,原始数据被发送给多GPU计算系统进行图像重建,完成后将重建图像传回.

|
图 2 磁共振图像扫描重建流程图 Figure 2 The work flow of MR image scan and reconstruction using multi-GPU computing system |
本节首先介绍利用GPU加速3D磁共振图像重建的设计思路,之后以3D SOS图像重建为例,展示重建算法的加速实现.
1.2.1 3D磁共振图像的加速重建设计磁共振扫描得到的原始数据称为k-space采样数据,3D扫描中存在三个扫描编码方向记作
| $ S({k_x}, {k_y}, z) = \int S ({k_x}, {k_y}, {k_z}){{\rm{e}}^{i2{\rm{ \mathsf{ π} }}({k_z}z)}}{\rm{d}}{k_z} $ | (1) |
| $ I(x, y, z) = F({k_x}, {k_y})S({k_x}, {k_y}, z) $ | (2) |
(1) 式表示将采集到的3D数据
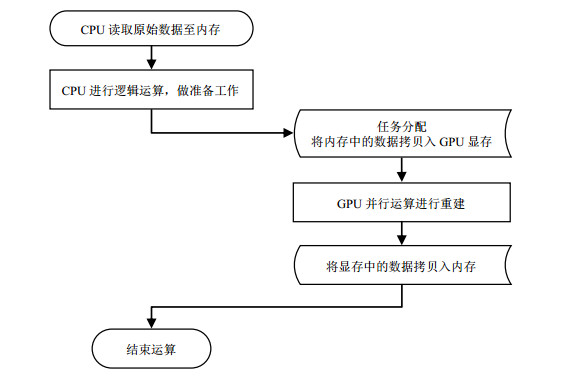
GPU并行重建各片层时流程如图 3所示.GPU并行重建每一个片层前,需将待处理的整块3D数据从内存拷贝至GPU显存,之后将GPU线程数设置为片层数,使这些线程并发执行,不同片层的重建时间重叠以达到加速效果.利用统一计算设备架构(CUDA)[10]编写的并行程序与基于CPU的串行循环程序在实现方式不同,这会导致对于数据存储空间的访问与读取方式不同.前者不同线程之间相互独立,GPU进行并行运算时,线程以不同的数据同时执行相同算法任务,GPU各线程处理的“不同数据”是从输入数据中截取而来:当输入数据存入GPU显存中后,线程根据其特有的线程编号,从显存的不同起始位置截取一定量的数据后进行运算.而CPU在执行串行循环程序时依赖程序上下文环境,按照规定的顺序和逻辑读取内存数据后进行处理,运算次序靠后的运算必须等待之前的运算处理完才进行.如果循环中运算过程相互独立,进行多次循环时,基于上下文产生的等待时间会极大降低重建效率.
|
图 3 CPU-GPU重建流程 Figure 3 CPU-GPU computing scheme |
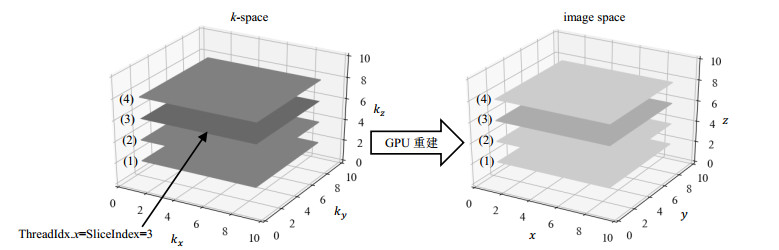
3D数据中不同片层的并行重建基本设计思路是启动多个GPU线程,每个线程同时重建3D数据中的不同片层,并行过程如图 4所示:整个重建过程可归纳为:寻址输入,算法重建,寻址输出.传输到显存中的3D磁共振扫描数据按照一定的规律储存,通常情况下按照逐片层的顺序,例如图中重建第三个片层的任务由3号线程负责,该线程会从显存开始位置跳过前两个片层的数据,找到第3个片层的开始位置,并从该位置起,将之后一个片层大小的数据拷贝到该线程私有的数据储存空间.重建的算法可以写成GPU能重复调用的_device_函数,图中3号线程调用该函数进行重建后,将处理结果根据线程编号插入到输出中的相应位置,即可实现3D磁共振图像重建的GPU加速.
|
图 4 GPU并行重建3D磁共振数据 Figure 4 Parallel 3D MR image reconstruction using GPU |
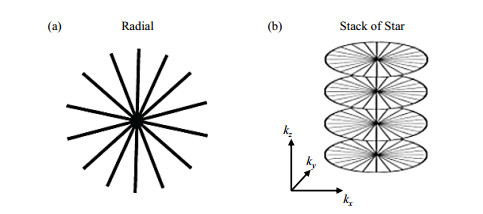
磁共振数据采集方式有多种,分为笛卡尔坐标采集与非笛卡尔坐标采集.非笛卡尔坐标采集中,常用的数据采集方式之一为在极坐标下沿径向采集磁共振数据,如图 5(a)所示:此时每一条采集的轨迹都交于中心原点.SOS成像方法是在
|
图 5 径向与Stack of Star(SOS)磁共振数据采集方式 Figure 5 Radial and Stack of Star (SOS) methods for MRI data acquisition |
SOS图像重建过程如下:利用(1)式在
(1)采样密度补偿
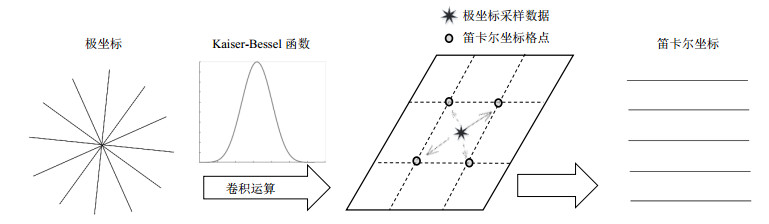
(2)引入卷积核函数进行卷积运算,将采样数据从极坐标空间转化到笛卡尔坐标空间(Regridding)
(3)傅里叶变换
(4)消除卷积核函数对图像影响.
在上述步骤中,第(1)步和第(4)步为图像质量优化步骤,第(1)步为采样数据的预处理,具体过程为归一化采样数据后,计算采样密度补偿系数,进行补偿.第(4)步将得到的图像结果除去卷积核函数在图像域中的信号以消除引入卷积核函数的影响,上述步骤运算相对简单,利用CPU即能在短时间内高效完成.整个重建中计算时间占比最大的是第(2)步Regridding,Regridding的数学表达如下:
| $ {F_g} = (FS) \otimes C $ | (3) |
|
图 6 Regridding过程 Figure 6 Regridding process |
每个2D片层的Regridding结果是该片层中的每个采样点进行Regridding后的累加所得,如(4)式所示.
| $ {F_g}(i, j) = \Sigma F(n){c_n} $ | (4) |
SOS图像重建消耗大量计算资源且计算时间较长,原因在于需要对于各片层中的每个采样点分别进行Regridding,当采样点较多时,串行依次计算每个采样点会造成严重的效率缺失[13].对于任意2D片层,不难发现其中每个采样数据Regridding过程都是相互独立的.利用GPU加速方法如下:假设每个片层的采集矩阵大小为

|
图 7 9个采样点的Regridding过程. (a)假设共需要Regridding 9个数据点;(b)二维线程网格中每个格点表示一个GPU线程,启动9个线程,每个线程处理一个数据的Regridding,所有线程并发执行 Figure 7 9-point Regridding process. (a) Situation of 9 data points; (b) Each grid on the right corresponds to one GPU thread and processes one data point concurrently |
在实际情况下,数据采集常常使用多通道线圈同时扫描,每个通道独立重建得到图像后,进行平方和开方运算得到最终的图像,如(5)式所示:
| $ f(x, y, z) = \sqrt {\sum\nolimits_{n = 1}^N {{f_n}{{(x, y, z)}^2}} } $ | (5) |
其中
所以3D重建实际上需要处理4D数据,以
SOS重建方法加速可以沿用3D各片层同时重建的设计思路,并且在此基础上进一步优化.因为该算法中不但各片层相互独立,其实所有采样点的Regridding都相互独立,启动
映射建立过程如下:首先整个Regridding的过程可以由(6)式表示:
| $ {C_{FOV \times FOV \times {K_z} \times CHA}} = f({R_{{K_x} \times {K_y} \times {K_z} \times CHA}}) $ | (6) |
其中
虽然待处理的重建矩阵有维度概念,但任意数据在计算机中都是以一段连续的字节储存(1D空间),矩阵的多维度对于计算机而言只是决定了矩阵中数据的相对储存位置.通常矩阵中的数据按照规定的维度顺序储存.图 8展示了一组3D磁共振数据
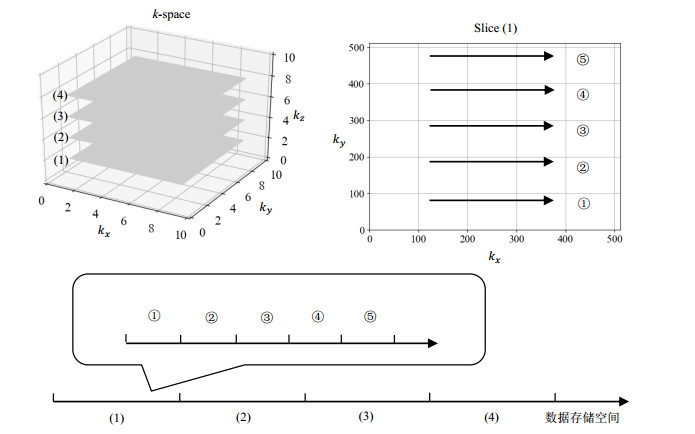
|
图 8 计算机储存3D磁共振数据示意图 Figure 8 Stores of 3D MRI data in computer memory |
当多维度矩阵的储存规则确定后,特定坐标的数据点在硬件存储空间的储存位置总是固定的.这种对应关系使GPU线程与采样点4D坐标的映射最终可以转化为1D GPU线程与1D显存的映射,而该映射关系可以自由设定.为简化,不妨将第N个GPU线程要处理的数据设置为显存中第N个输入数据,该采样点对应的4D空间坐标
| $ \left\{ \begin{array}{l} CHA = \left[ {\frac{N}{{{K_x} \times {K_y} \times {K_z}}}} \right]\\ {E_2} = \left[ {\frac{{N - CHA \times {K_x} \times {K_y} \times {K_z}}}{{{K_x} \times {K_y}}}} \right]\\ {E_1} = \left[ {\frac{{N - CHA \times {K_x} \times {K_y} \times {K_z} - {E_2} \times {K_x} \times {K_y}}}{{{K_x}}}} \right]\\ {E_0} = N - CHA \times {K_x} \times {K_y} \times {K_z} - {E_2} \times {K_x} \times {K_y} - {E_1} \times {K_x} \end{array} \right. $ | (7) |
(7) 式中[ ]为取整符号.
GPU第N个线程从显存中读出4D空间中坐标为
完成以后最终根据

|
图 9 GPU线程与显存映射示意图,一个GPU线程处理一个极坐标数据,Regridding后,极坐标数据化为多个笛卡尔坐标加权表示,所以一个线程对应一个输入,但影响多个输出 Figure 9 Schematic diagram of GPU thread and memory mapping: Each GPU thread processes single input data but has influence on multiple outputs |
输出
| $ I = {E'_0} + {E'_1} \times FOV + {E'_2} \times FOV \times FOV + CHA \times FOV \times FOV \times {K_z} $ | (8) |
如此加速算法带来高并行性的同时,会增加GPU显存的负担,由于显存也有一定的上限,所以对并行重建任务需要进行划分.本文中计算系统有两块GPU,所以任务按片层数量对半划分.在程序的执行上,需保证两块GPU的重建是并行开展的,否则配置多GPU就失去了意义,结合基于多核CPU的fork/join并发模式[15]可以实现这点,如图 10所示:fork意为分叉,即将一个大任务分割成若干小任务;join意为汇总,即汇总每个小任务后得到大任务的结果.该模式刚开始执行时,只有主线程存在,当遇到需要并行计算的时候,会派生出若干子线程同时执行计算,并行执行结束后,子线程终止退出,将控制权返回主线程.fork/join支持多级执行,将计算任务分成若干小任务后,还可以其中的小任务再进行划分,直至最终可以顺利执行为止.

|
图 10 fork/join并发模式 Figure 10 fork/join concurrent mode |
本文中fork/join模式并不用来进行具体的重建工作,而是利用多核CPU派生出的子线程控制不同的GPU硬件进行并行运算.派生CPU线程的方式有多种,在此运用OpenMP[16]辅助编译,它是一种可将串行程序的增量编程转化为并行的技术,由编译器负责处理线程派生、初始化、终止等复杂实现细节.
多GPU分布式系统加速3D SOS图像重建的完整流程如图 11所示.在各步骤中,采样密度补偿为预处理过程,输入原始数据,得到补偿后数据,之后所有的计算都基于补偿后的数据进行,使用GPU实现该步骤会导致输入数据与计算中间过程占据显存空间,额外的显存释放过程会造成时间消耗,另外采样密度补偿涉及数据的归一化,利用了数据的关联性,该过程无法进行并行优化,因此对于类似的数据预处理任务,CPU的处理性能更优.之后利用GPU在

|
图 11 多GPU分布式计算系统加速3D SOS图像重建 Figure 11 Multi-GPU distributed computing accelerates 3D SOS MR image reconstruction |
为验证多GPU分布式图像重建的加速性能,本文设计了两组实验,每组实验分别利用SOS方法采集10个3D磁共振原始数据,在同一组实验中,保持每个3D数据的各个片层采集矩阵相同,仅改变扫描片层数,在不同组别间使用差异化的采集矩阵.第一组数据的每个片层采集矩阵为600×600,扫描对象为人脑,第二组数据的每个片层采集矩阵为480×480,扫描对象为带网格的长方形水模,参数如表 1所示.对于每组实验数据,分别使用CPU进行逐片层重建(方法Ⅰ)与本文建议的多GPU分布式重建方法(方法Ⅱ)进行图像重建,并对比两者的成像速度,值得一提的是Gadgetron软件框架对于基于CPU的矩阵运算进行了多线程优化,所以方法Ⅰ在重建每一个片层时实际使用了多核CPU资源.
| 表 1 基础实验参数 Table 1 Experimental parameters |
表 2与表 3分别展示在不同采集矩阵下,利用方法Ⅰ和方法Ⅱ进行3D SOS图像重建所用的时间,表中将该算法中最耗时的Regridding部分单独展示.
| 表 2 600×600采集矩阵下人脑扫描3D SOS图像重建时间 Table 2 3D SOS human brain MR image reconstruction consumption time with sampling matrix of 600x600 |
| 表 3 480×480采集矩阵下水模扫描3D SOS图像重建时间 Table 3 3D SOS water model MR image reconstruction consumption time with sampling matrix of 480×480 |
图 12、13分别展示了方法Ⅰ和方法Ⅱ部分片层的图像重建结果,对比两种方法的成像结果,并无视觉上的差异,因此利用方法Ⅱ进行加速不会对图像质量造成影响.

|
图 12 人脑扫描3D SOS重建图像(片层采集矩阵=600×600) Figure 12 Human brain MR images reconstructed by SOS sampling (matrix=600×600) |

|
图 13 水模扫描3D SOS重建图像(片层采集矩阵=480×480) Figure 13 Water model MR images reconstructed by SOS sampling (matrix=480×480) |
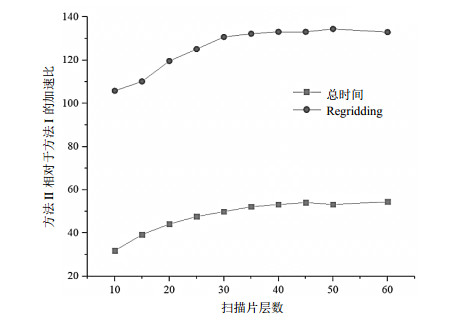
表 2中不同片层数量条件下,利用多GPU分布式重建获得的加速性能如图 14所示.
|
图 14 多GPU分布式重建的加速性能 Figure 14 Acceleration performance of multi-GPU distributed reconstruction |
应用方法Ⅱ相比方法Ⅰ进行SOS图像重建可以获得数十倍以上的加速,尤其在Regridding部分体现得格外明显.当重建的片层数变大时,加速比先增加后趋于稳定,原因是在片层数较少时,待处理的数据总量较小,总的重建时间较少.此时在方法Ⅱ中,将重建任务分配给多个GPU需要执行额外的多线程同步、内存与GPU显存之间的数据通信,该时间成本在总时间中占比较大.当重建时间随着数据量的增加而增加时,任务分配对于重建的影响逐渐降低,使得加速比增加,然而加速比有一定上限,因为SOS图像重建中所有采样点的计算非完全独立,方法Ⅱ中每一个极坐标采样点并行Regridding后需要与同片层其他采样点的计算结果进行累加,得到该片层的运算结果.累加为串行过程,相对耗时,因此其决定了方法Ⅱ中Regridding的总时间.累加的具体执行时间取决于计算量,即每个2D片层的采集矩阵,所以当采集矩阵确定时,能达到的加速上限也就确定了.
结合表 2和表 3分析,对于不同的采集矩阵,在相同的数据处理量下所能达到的加速比不同:当片层采集矩阵较小时,对于任意采样点来说,同一片层的其它采样点较少,计算关联性相对较小,使得并行性提高.如图 15(a)所示.采集矩阵较小时,Regridding的加速比上限明显高于较大采集矩阵条件下的加速比上限.但是在方法Ⅱ中,因为Regridding用时相对较少,随着数据量的增加,傅里叶变换的时间在重建总时间中占比不断增加,弱化了Regridding对于总时间的影响,如图 15(b)所示.即使在不同采集矩阵下,总时间的加速比在趋于平稳时差别较小.
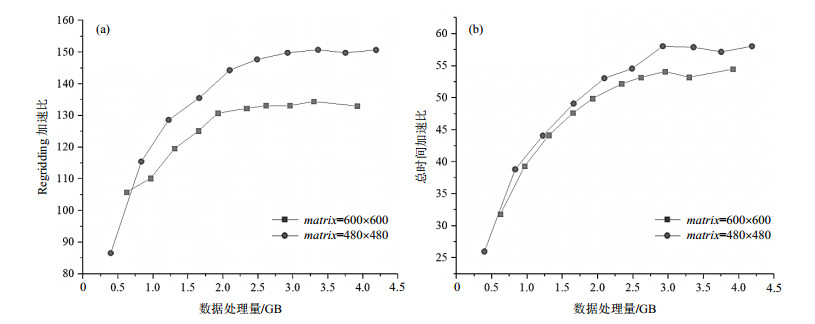
|
图 15 不同采集矩阵下,使用方法Ⅱ相对于方法Ⅰ对相同数据处理的加速比. (a) Regridding的加速比;(b)重建全过程的加速比 Figure 15 Acceleration ratio of the same amount of data processed with different sampling matrices. (a) Regridding acceleration ratio; (b) Whole process acceleration ratio |
对比利用网络通信连接起来的多台计算机组成的计算系统,多GPU分布式计算不需要进行额外的网络维护,在计算任务的分配上,任务的分配与整合过程也更为简化.在数据传输上,将多GPU置于同一机箱,数据通过PCI-E总线进行传输通信,相比网络传输,在传输速度以及可靠性上要高得多,这为该系统在磁共振算法开发研究与临床中的应用打下了基础.
在磁共振图像重建中,内存是决定能否进行高效重建的重要因素.CPU重建中,磁共振原始数据、重建结果以及所有重建中间过程的数据储存开支都由内存承担,应用复杂算法重建较大的数据时,长时间的高内存使用率会使得系统响应变得极为缓慢,系统超负荷时重建时间会随着数据量的增加非线性大幅增加,由此内存需求伴随算法复杂度的增加而增加.在多GPU分布式计算中所有并行计算产生的数据存储负荷均由GPU的显存承担,可以根据显存的大小制定不同的任务分配计划,使其高效运行.计算机内存只需负责原始数据,输出数据以及少量中间计算过程的存储,磁共振扫描数据的大小取决于扫描时间相对可控,致使内存使用率始保持在平稳较低的范围内,从而减弱了重建算法对于内存的依赖.
在本文中,SOS图像重建的并行计算任务只进行了一次分配,将任务分为两份,如图 16(a)所示:考虑极端情况,重建的算法极为复杂或者数据处理量极大,可以将并行计算任务分成多份.分配方法可分为纵向拓展[图 16(b)]与横向拓展[图 16(c)].
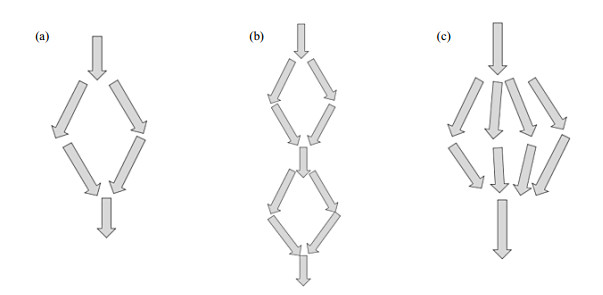
|
图 16 SOS图像重建的任务分配模式. (a)本文中SOS的任务分配模式;(b)纵向拓展分配模式;(c)横向拓展分配模式 Figure 16 Task distribution modes of SOS MR image reconstruction. (a) SOS task distribution in this research; (b) Vertical expansion distribution; (c) Transversal expansion distribution |
纵向拓展中,不增加GPU的数量,将计算任务进行多次分配汇总,在这种情况下,GPU存在显存上限不会造成重建的失败,只会使得计算的并行性降低,另外多次任务分配需要额外的线程同步时间.横向拓展中,将计算任务一次分配为多份,如此并行性不会降低,计算性能较好,但需要增加GPU的数量,增加硬件成本.不论是纵向还是横向拓展,如果待重建的数据大小不变,对于计算机内存没有额外的开销.
3 结论本文设计介绍了3D磁共振图像重建的分布式GPU并行程序设计方法,除了文中提到的SOS图像重建,也能运用到其他3D图像重建算法中,具有通用性.以SOS图像重建为例,对比CPU与多GPU分布式重建的算法执行速度,可以证明该分布式重建方式可以充分利用计算资源,发挥异构机器的性能特点,极大地加速算法执行.将它与其他重建算法实现方式比较,分析可以发现其硬件成本相对较低、易于维护、有较好的扩展性.
未来随着GPU硬件与编程技术的发展与普及,相信基于Gadgetron平台与多GPU的分布式图像重建可以更加广泛地服务于磁共振图像重建算法的研发,最终应用到临床快速MRI扫描中.
| [1] | KECSKEMETI S, JOHNSON K, WU Y J, et al. High resolution three-dimensional cine phase contrast MRI of small intracranial aneurysms using a stack of stars k-space trajectory[J]. J Magn Reson Imaging, 2012, 35(3): 518-527. DOI: 10.1002/jmri.v35.3. |
| [2] | LUSTIG M, DONOHO D, PAULY J M. Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med, 1999, 58(6): 1182-1195. |
| [3] | HANSEN M S, SØRENSEN T S. Gadgetron:an open source framework for medical image reconstruction[J]. Magn Reson Med, 2013, 69(6): 1768-1776. DOI: 10.1002/mrm.24389. |
| [4] | XUE H, INATI S, SØRENSEN T S, et al. Distributed MRI reconstruction using Gadgetron-based cloud computing[J]. Magn Reson Med, 2015, 73(3): 1015-1025. |
| [5] | KALINOV A, LASTOVETSKY A, ROBERT Y. Heterogeneous computing[J]. Parallel Computing, 2005, 31(7): 649-652. DOI: 10.1016/j.parco.2005.04.001. |
| [6] | SORENSEN T S, SCHAEFFTER T, NOE K O, et al. Accelerating the nonequispaced fast Fourier transform on commodity graphics hardware[J]. IEEE Trans Med Imaging, 2008, 27(4): 538-547. DOI: 10.1109/TMI.2007.909834. |
| [7] | COOK S. CUDA programming:A developer's guide to parallel computing with GPUs[M]. Waltham MA: Elsevier, 2012. |
| [8] | HANSEN M S, SØRENSEN T S. Gadgetron users guide v3. 8. 2[OL]. [2014-11-06]. https://sourceforge.net/p/gadgetron/home/Manual/. |
| [9] | NVIDIA. Programming guide[OL]. [2018-3-5]. https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#compute-capability. |
| [10] | STORTI D, YURTOGLU M. CUDA for engineers[M]. New Jersey: Addison-Wesley, 2016. |
| [11] | WRIGHT K L, HAMILTON J I, GRISWOLD M A, et al. Non-cartesian parallel imaging reconstruction[J]. J Magn Reson Imaging, 2014, 40(5): 1022-1040. |
| [12] | PIPE J. Gridding for non-cartesian k-space sampling[C]//Seattle: International Society for Magnetic Resonance in Medicine(ISMRM), 2006. |
| [13] | SEDARAT H, NISHIMURA D G. On the optimality of the gridding reconstruction algorithm[J]. IEEE Trans Med Imaging, 2000, 19(4): 306-317. DOI: 10.1109/42.848182. |
| [14] | KANDROT E, SANDERS J. CUDA by example[M]. Amsterdam: Addison-Wesley Longman, 2010. |
| [15] | LEA D. A Java fork/join framework[C]//Association for Computing Machinery(ACM) conference. Texas: ACM Press, 2000. |
| [16] | BARLAS G. Multicore and GPU programming[M]. Waltham MA: Elsevier, 2015. |
 2018, Vol. 35
2018, Vol. 35 
