2. 中国科学院大学, 北京 100049;
3. Center of Interdisciplinary Magnetic Resonance, National High Magnetic Field Laboratory, 1800 East Paul Dirac Drive, Tallahassee, FL 32310, USA
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Center of Interdisciplinary Magnetic Resonance, National High Magnetic Field Laboratory, 1800 East Paul Dirac Drive, Tallahassee, FL 32310, USA
化学位移相互作用是核磁共振(Nuclear Magnetic Resonance, NMR)波谱学中最重要的参数之一.化学位移张量或屏蔽张量对局部电子环境非常敏感[1-3],通常包括各向同性化学位移和化学位移各向异性(Chemical Shift Anisotropy, CSA)张量.对于粉末样品,各向异性使谱线增宽,魔角旋转可平均掉各向异性相互作用,从而窄化谱线提高谱图分辨率.但CSA张量包含许多结构与动力学信息[4],为获得这些信息,研究者们已提出许多方法用于测量1H、13C与15N等核的CSA.
1H CSA是探测物质结构以及氢键的重要探针,报道指出1H CSA张量与其氢键长度存在一定联系[5-13],也与蛋白质的二级结构相关[14].然而,测量1H CSA的实验数量有限,且以小分子为主.由于1H-1H同核偶极耦合相互作用非常强,以及1H CSA范围较小,测量1H CSA比13C与15N核更加困难,以固体大分子为研究对象的1H CSA测量更是面临巨大挑战.
最早的1H CSA测量可追溯到1969年,Haddix与Lauterbur [15]使用传统的质子连续波(Continuous Wave, CW)去耦法测量单晶三氟乙酸中的1H CSA.Moroz等[16]在1983年使用粉末线型法测量固体复合材料中HF的1H CSA,之后慢速魔角旋转下单脉冲激发傅里叶变换核磁共振氢谱(Fourier Transform 1H NMR, 1H FT-NMR)被用来测量晶体水合物1H CSA[17].之后,有研究者尝试测量含有少量质子的小分子的1H CSA,通过多脉冲同核去耦(Multiple-Pulse Homonuclear Decoupling)技术有效地压制质子间强同核偶极耦合相互作用[18],结合旋转与多脉冲去耦序列方法(Combining Rotation And Multiple-Pulse Decoupling Spectroscopy, CRAMPS)能够获取高分辨率的1H CRAMPS谱,然后利用结合慢速魔角旋转的方法得到旋转边带,通过拟合边带最终获得1H CSA.但该方法需多脉冲去耦,并且要求魔角旋转速度比CSA更小,因此只适用于具有少数质子位点的小分子[19, 20].克服同核偶极耦合的另一个方法是选择氘代样品.1976年,Pines、Ruben、Vega与Mehring[21, 22]首次利用激发氘核(2H)双量子跃迁去耦2H-1H偶极耦合相互作用,通过单脉冲1H谱测量了氘代冰的1H CSA张量. Vega等[23]利用相同原理激发2H双量子跃迁测量了单晶的1H CSA.Achlama等[24-26]将传统2H FT-NMR应用于氘代样品中来得到氘核四极裂分,从而获取2H CSA张量.另一项研究[27]在魔角旋转与转动共振(Rotary Resonance)条件下,于二维1H-1H相关实验的间接维重新引入1H CSA,该方法对射频场(B1)不均一性非常敏感,如果B1均一性不够高,会影响1H CSA张量测量的准确性.最近,Ramamoorthy等[28, 29]提出用质子检测三维超快(Ultrafast)魔角旋转固体NMR实验来测量小分子氨基的1H CSA.
对于大分子,例如蛋白质,快速魔角旋转下化学位移各向异性重耦技术更加实际可行.2013年,侯广进等[8, 30]在快速魔角旋转条件下,应用三维对称重耦序列(RNnν型脉冲序列)实验得到完全13C-15N标记的CAP-Gly蛋白氨基的1H CSA张量.2017年,本文作者[14]提出一种基于xCSA序列化学位移放大方法,用以测量蛋白质氨基1H CSA.在液体NMR中,虽然CSA被分子翻转所平均,谱线变窄,但CSA信息仍与各向同性信号的核自旋弛豫时间(T1或T2)有关.特别是在高磁场下的球状蛋白质研究中,这种关系尤为显著.所以液体NMR中也发展出通过从弛豫时间中提取球状蛋白质氨基的1H CSA的方法[5, 10, 11].
近年来,许多计算多肽、核酸与蛋白质1H CSA的高精度量子化学方法[31-36]被提出.理论计算能够准确的验证1H CSA与氢键及二级结构之间的关系.如ab initio计算方法证明氢键结构与1H CSA张量组分及方向存在一定联系[7, 37-39].ab initio计算方法也暗示氨基1H CSA张量与氢键长度的联系可能会更加复杂.例如,Sharma等[37]发现1H CSA张量组分除却与氢键长度有关外,还与氢键角度有一定关系.Parker等[38]从密度泛函理论(Density Functional Theory,DFT)计算方法中得出,虽然影响CSA最重要的因素是氢键结构,但是更远距离的氢键网络也会对CSA有显著贡献.另外,Suzuki等[39]最近基于他们的计算结果发现,蛋白质中氨基质子各向同性化学位移差异的本质原因是C=O的磁各向异性作用.通过计算分子中1H CSA可以有效确定与改进分子结构,计算的结果与实验结果经常相互验证.
经过数十年的发展,测量CSA张量的方法主要包括单晶静态谱测量、多晶样品静态粉末线型拟合、慢速魔角旋转旋转边带拟合、基于多维的化学位移各向异性重耦技术以及量子化学计算方法等.CSA包含了很多结构信息,所以研究者对1H CSA的测量一直极具热情,目前小分子中1H CSA测量技术与方法日趋完善,但是对于大分子,例如蛋白质、蛋白质复合物、DNA与RNA等的1H CSA仍存在挑战,虽有少数方法被提出,但是未来仍是研究重点.
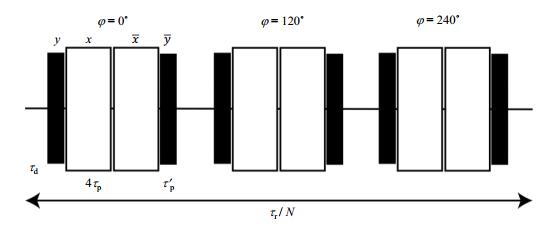
1 研究进展 1.1 慢速魔角旋转法测量1H CSA20世纪90年代,Nielsen等[20]首次提出结合MSHOT-3同核多脉冲去耦CRAMPS谱,用于测量小分子多晶粉末,如己二酸、氢氧化钙、丙二酸与硫酸氢钾的1H CSA张量,其所用脉冲序列如图 1所示.由于所测样品1H CSA较小,所以魔角旋转转速必须小于样品1H CSA才能产生旋转边带,进而通过拟合旋转边带获得1H CSA张量参数.
|
图 1 使用MSHOT-3同核去耦CRAMPS谱测量1H CSA的脉冲序列.黑色实心矩形代表π/2脉冲,空心矩形代表 2π脉冲.τd为延迟时间,τp与τp'分别为两个π/2脉冲的脉宽,τr为转子周期,整个脉冲序列与转子同步,整数N(大于3)表示一个转子周期中MSHOT-3循环的个数.图与说明出自文献[20] Figure 1 Timing scheme of the MSHOT-3 homonuclear decoupling sequence employed for the determination of magnitudes of 1H CSA using CRAMPS. Filled bars represent π/2 pulse sequences, and open bars represent 2π pulse sequences. τd represents the delay, τp and τp' are the durations of effective 90˚ pulses. The pulse sequence is rotor synchronized to an integral number N (larger than 3) of MSHOT-3 cycles within the rotor period. The figure and caption reproduced from reference [20] |
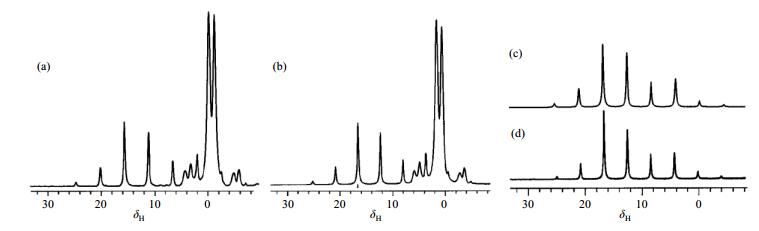
图 2(a)为己二酸使用MSHOT-3多脉冲同核去耦的1H CRAMPS(400 MHz)谱图.谱图显示己二酸中两个位点1H核的旋转边带.图 2(b)为使用洛伦兹线型去卷积得到的羧基质子信号峰旋转边带与使用洛伦兹/高斯线型去卷积得到亚甲基质子信号峰旋转边带.通过去卷积可以区分羧基与亚甲基质子重叠的旋转边带,获得各自单组份旋转边带便可以进行拟合.图 2(c)为去卷积谱得到的羧基质子旋转边带.通过图 2(c)的旋转边带,迭代拟合可以得到图 2(d)所示的模拟的1H旋转边带谱.
|
图 2 (a) 己二酸使用MSHOT-3多脉冲同核去耦的1H CRAMPS(400 MHz)谱.实验使用图 1脉冲序列,魔角旋转转速为584 Hz,N=18,τp = 2.2 μs, τp' = 2.55 μs, 延迟时间为128 s,累加次数为64次; (b)去卷积谱,洛伦兹(羧基质子),洛伦兹/高斯(亚甲基质子); (c)单独羧基质子的去卷积谱; (d)使用(c)中去卷积谱拟合得到的1H旋转边带.图与说明出自文献[20] Figure 2 (a) 1H CRAMPS (400 MHz) spectrum of adipic acid recorded using MSHOT-3 multiple-pulse decoupling method. The experimental pulse sequence was shown in Fig. 1 with magic angle spinning speed=584 Hz, N=18, tp = 2.2 μs, τp' = 2.55 μs, relaxation delay=128 s, scan number=64; (b) Deconvoluted spectrum using Lorentzian (for carboxylic protons) and Lorentzian/Gaussian lineshapes (for methylene protons); (c) Deconvoluted spectrum for the carboxylic protons only; (d) Simulated 1H spectrum resulting from fitting of the spectrum in (c). The figure and caption reproduced from reference [20] |
同核去耦慢速魔角旋转方法可以测量1H CSA参数,但一般只适用于具有少数质子位点的小分子,如果样品中质子位点较多,且化学位移接近,使用去卷积也不能够准确分析各自位点的旋转边带.
1.2 超快魔角旋转法测量1H CSA测量1H CSA的最大挑战之一便是样品中存在非常强的1H-1H同核偶极耦合相互作用,而超快魔角旋转能够有效的去除掉大部分同核偶极耦合.基于此原理,许多结合超快魔角旋转测量1H CSA的方法被提出.
2013年,Titman等[40]提出各向异性-各向同性化学位移相关二维固体1H NMR实验.该实验在超快魔角旋转(转速 > 50 kHz)条件下完成,使质子各向同性化学位移在检测维具有非常好的分辨率.脉冲序列采用R1632对称重耦序列,将1H CSA在间接维重新引入.该实验被用于测量酪氨酸·盐酸与柠檬酸中羟基氢键的1H CSA.
由于提取直接与14N核连接的1H CSA时,14N-1H异核耦合也会被重聚,而且缺乏有效的手段将这些相互作用去耦.2015年,Pandey与Nishiyama[41]提出一种测量天然丰度L-组氨酸盐酸盐·水物样品1H CSA方法.他们使用比14N四极耦合常数小约30倍的射频场来进行“on-resonance” 14N-1H去耦,从而有效的消除了14N-1H异核耦合.实验使用魔角旋转转速为90 kHz,化学位移各向异性重耦序列为R1887.
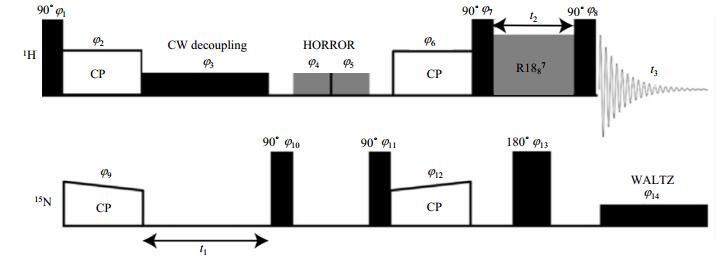
最近Ramamoorthy等[42]提出一种利用超快魔角旋转2D 1H/1H CSA/CS相关谱方法,基于转子同步的π脉冲编码CSA,使1H CSA线型不会失真且效率较高.随后,他们在此种方法基础上又提出3D 1H/1H/1H CSA/CSA/CS相关实验[43],在超快魔角旋转条件下,通过1H/1H RFDR(Radio Frequency-Driven Recoupling)来提取两个相关1H CSA张量的相对取向.然而2D 1H/1H CSA/CS实验由于缺少1H CS维的分辨率,无法用于测量氨基1H CSA,所以该研究组又提出一个3D 15N/1H/1H CS/CSA/CS相关实验(转速为70 kHz)[28],通过15N各向同性化学位移可得到点分辨率的1H CSA.质子检测3D 15N/1H/1H CS/CSA/CS相关实验脉冲序列如图 3所示.质子磁化矢量通过交叉极化转移到15N核,在t1时间内15N核化学位移发生演化,期间在质子通道进行低功率CW去耦,用于去除1H-15N异核偶极耦合相互作用.残余的质子横向磁化矢量通过同核转动共振序列(HORROR)消除,之后15N核磁化矢量通过交叉极化又转回1H核,HORROR之前的15N π/2脉冲使15N磁化矢量回到纵向,以避免15N核随时间演化与15N核磁化矢量横向驰豫,随后施加1H π/2脉冲将1H核磁化矢量保持在z轴,使用对称R1887脉冲来重聚质子化学位移各向异性.在化学位移各向异性重聚期间,施加15N π脉冲去除15N-1H异核耦合.
|
图 3 质子检测3D 15N/1H/1H CS/CSA/CS脉冲序列.图与说明出自文献[28] Figure 3 Proton-detected 3D 15N/1H/1H CS/CSA/CS pulse sequence. The figure and caption reproduced from reference [28] |
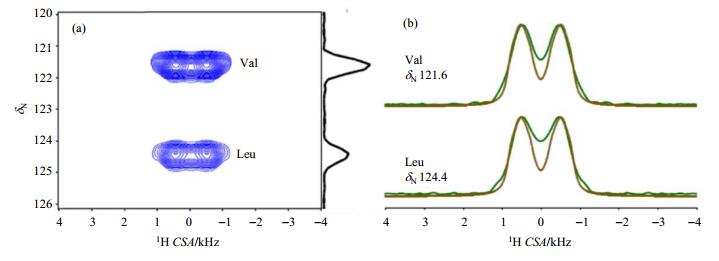
实验样品为N-乙酰-15N-L-缬氨酰-15N-L-亮氨酸(N-acetyl-15N-L-valyl-15N-L-leucine,NAVL),为避免缬氨酸与亮氨酸氨基质子的重叠,所以需要加入高分辨率15N维.在3D 15N/1H/1H CS/CSA/CS实验谱图中提取的2D F1/F2(15N/1H CS/CSA)投影如图 4(a)所示,随后在缬氨酸与亮氨酸残基15N核化学位移处提取平行1H CSA维的谱线(绿色),最后通过数值模拟得到实验1H CSA线型,如图 4(b)所示.测量得到的1H CSA参数为——缬氨酸:各向同性化学位移δiso = 9.0,化学位移各向异性δaniso = 9.1,不对称参数η = 0.7;亮氨酸:δiso = 9.2,δaniso = 9.1,η = 0.7.
|
图 4 (a) 从NAVL样品3D 15N/1H/1H CS/CSA/CS谱提取的2D F1/F2(15N/1H CS/CSA)投影;(b)在缬氨酸(Val)与亮氨酸(Leu)残基15N核化学位移处平行1H CSA维的谱线(绿色),以及相应的数值模拟线型(棕色).图与说明出自文献[28] Figure 4 (a) Two-dimensional F1/F2 (15N/1H CS/CSA) projection extracted from the 3D 15N/1H/1H CS/CSA/CS spectrum of NAVL; (b) Spectral slices (green) taken parallel to the 1H CSA dimension at the 15N chemical shifts of Val and Leu residues of NAVL, and corresponding simulated line shapes (brown). The figure and caption reproduced from reference [28] |
质子检测3D 15N/1H/1H CS/CSA/CS脉冲实验可以有效测量二肽NAVL的氨基1H CSA参数,该方法有希望应用于更多更复杂的体系中,但是最大的挑战是1H核化学位移是否具有足够分辨率.另外该方法如结合氘代样品、更高磁场强度以及更高魔角旋转转速(转速 > 100 kHz),便可更大程度上减少谱分辨率的问题,从而有可能应用于大分子体系.
1.3 快速魔角旋转测量1H CSA快速魔角旋转(10~20 kHz)条件下,进行1H CSA测量一般有两类脉冲序列:一种为RNnν型脉冲序列[8];另一种为xCSA脉冲序列[14].两种方法均可用于蛋白质氨基1H CSA的测量.
1.3.1 RNnν重耦方法RNnν型脉冲序列,即对称重耦序列(Symmetry-Based Recoupling Sequence).此类型脉冲序列是根据包含重复N/2次若干对π脉冲πφπ-φ对称法则而设计,其相位为φ = πν/N [44].依据射频脉冲与空间样品旋转的对称特性,可将特定的自旋相互作用重耦.例如R1825脉冲序列可重耦化学位移各向异性与异核偶极耦合相互作用,不能重耦各向同性化学位移、同核偶极耦合相互作用与J耦合[6].对耦合自旋施加去耦射频辐射脉冲,可以去除重耦的异核偶极耦合相互作用,只在重耦之后保留化学位移各向异性相互作用.基于对称的R1825脉冲序列能够提供选择性重耦,也可压制较强的同核偶极耦合相互作用.之前有研究者使用基于对称重耦序列在间接维将1H CSA重新引入,此二维实验在直接维将每个单独的1H位点按照其自身各向同性化学位移进行区分[6],然而该方法的限制仍较为比较明显:采样期间需要施加非常强的同核去耦射频场;基于对称重耦序列需要相对较慢的魔角旋转.
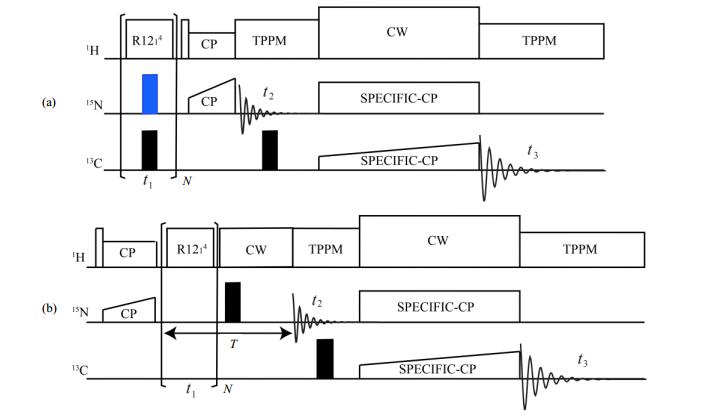
侯广进等使用R1214脉冲序列与3D实验相结合的脉冲序列[8],如图 5所示.测量U-13C-15N标记CAP-Gly蛋白氨基1H CSA参数.R1214是一种RNnν对称型脉冲序列,可以重耦化学位移各向异性与异核耦合相互作用,并且可以抑制各向同性化学位移与同核偶极耦合[6, 45].图 5脉冲序列中包含3个独立的NMR实验,通过拟合3个实验谱图,可以提取出精确的1H CSA张量,还可以获得1H-15N偶极耦合常数以及CSA张量与N-H键矢量之间的相对取向信息.这些信息对蛋白质分子结构的精确测量具有重要意义.
|
图 5 (a) R1214-1H(15Nund)与R1214-1H(15Ndec)实验脉冲序列;(b) 3D R1214-15N实验脉冲序列.魔角旋转下,在t1演化时间施加转子同步的R1214射频脉冲重新引入1H CSA与1H-15N偶极耦合相互作用.空心矩形和实心矩形分别代表π/2和π脉冲.(a)中t1时间施加15N去耦π脉冲与否,可代表两种实验,施加:R1214-1H(15Ndec);不施加:R1214-1H(15Nund).使用短时间交叉极化接触时间来选择性监测氨基15NH中的1H核.(b)中在恒时T内重聚化学位移进行15N横向磁化矢量时间演化的监测,t2演化后进行15N-13C选择性交叉极化,最后在t3检测13C信号.图与说明出自文献[8] Figure 5 Pulse sequences for (a) R1214-1H(15Nund) and R1214-1H(15Ndec); (b) R1214-15N 3D experiments. Rotor synchronized symmetry RF pulses are applied during t1 evolution time to reintroduce 1H CSA or 1H-15N dipolar interactions under MAS conditions. Empty and solid rectangles denote π/2 and p pulses, respectively. In fig. (a), the time dependence of 1H z-magnetization is monitored, either with application of the 15N decoupling π pulses [R1214-1H(15Ndec)] or without [R1214-1H(15Nund)]. Site selective 1H detection is accomplished by short-contact-time CP to 15N. In fig. (b), the time evolution of 15N x-magnetization is monitored with refocusing of the chemical shift over a constant evolution period T. 15N-13C SPECIFIC-CP magnetization transfer is introduced following the t2 evolution period, with the subsequent detection of the 13C signal during the t3. The figure and caption reproduced from reference [8] |
图 6为从3D R1214-1H(15Ndec)谱提取的2D NCA平面与CAP-Gly蛋白6个典型残基,可见谱图分辨率与信噪比均较好,谱图中可以提取出42个CAP-Gly残基氨基1H CSA.

|
图 6 (a) U-13C, 15N-CAP-Gly蛋白的3D R1214-1H(15Ndec)谱图的2D NCA平面(t1=0);(b)从3D RN-1H(15Ndec)谱中提取的RN-1H(15Ndec)线型,所取残基位点为:H40 (β-折叠), Y46 (β-折叠), V47 (β-折叠), T50 (β-折叠), G67 (loop), 与C81 (loop).图与说明出自文献[8] Figure 6 (a) The 2D NCA plane (at t1 = 0) of the 3D R1214-1H(15Ndec) spectrum of U-13C, 15N-CAP-Gly domain of mammalian dynactin; (b) Experimental RN-1H(15Ndec) line shapes extracted from the 3D RN-1H(15Ndec) spectrum for judiciously chosen CAP-Gly residues: H40 (terminus of β-sheet), Y46 (β-sheet), V47 (β-sheet), T50 (β-sheet), G67 (loop), and C81 (loop). Figure and caption reproduced from reference [8] |
图 7为U-13C-15N标记CAP-Gly蛋白1H CSA张量主值分量与氢键长度的关系.根据Tjandra与Bax的研究,1H CSA中
| $ {\delta _{XX}} - {\delta _{YY}} = B + \frac{C}{{{{({r_{{\rm{H}} - {\rm{O}}}} - D)}^2}}} $ |

|
图 7 U-13C, 15N-CAP-Gly蛋白1H CSA张量主值分量与氢键长度的关系.(a)与(b)分别为张量跨度δXX-δYY与H⋯O/N⋯O长度关系图. (c)与(d)分别为张量主值分量δXX(红色)、δYY(灰色)、δZZ(蓝色)与H⋯O/N⋯O长度关系图.图与说明出自文献[8] Figure 7 Correlation between principal components of 1H CSA tensors and hydrogen bond length in U-13C, 15N-CAP-Gly domain of mammalian dynactin. (a) and (b) show the correlations between the span, δXX-δYY and the H⋯O and N⋯O distance, respectively. In (c) and (d), correlations of the principal components δXX (red), δYY (grey), and δZZ (blue) are shown with the H⋯O and N⋯O distance, respectively. The figure and caption reproduced from reference [8] |
从图 7中可以看出,数据点具有很大的分散度,根据ab initio计算得出的结论,氢键距离可能不完全由1H CSA张量决定,为获得深入理解,需要进行更多1H CSA与氢键参数相关的实验.
综上所述,侯广进等人提出了一种测量蛋白质氨基1H CSA的可靠方法:间接维使用R1214序列重新引入1H CSA,直接维为15N或13C核的化学位移,从而实现残基位点分辨率的3D NMR实验.
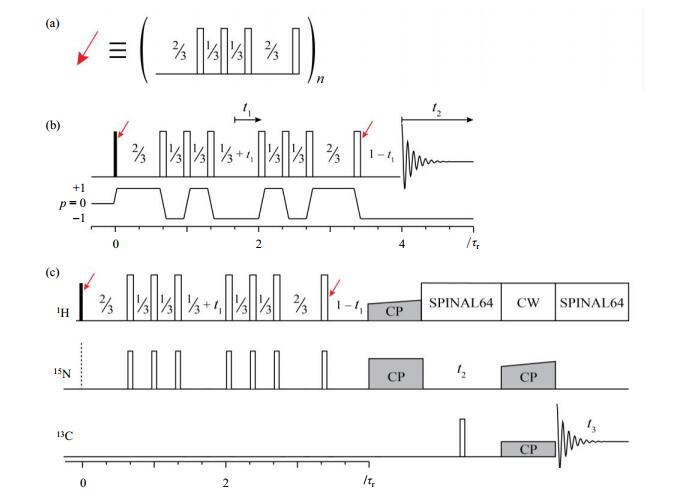
1.3.2 xCSA放大方法化学位移各向异性放大技术(CSA amplification)是利用一系列π脉冲,将原本在魔角旋转下已被平均掉的化学位移各向异性“扰乱”,达到将化学位移各向异性相互作用重新引入的目的,该脉冲序列是由Gullion[46]与Griffin[47]等研究者首先提出的.其中π脉冲需要按照特定时序设计并排列,磁化矢量通过演化可以产生旋转边带,得到的旋转边带与通过降低魔角旋转转速得到的旋转边带,或样品某位点CSA被放大得到的旋转边带是相同的,所以该方法也被称为放大化学位移调制(Extended Chemical Shift Modulation)或CSA放大技术(CSA Amplification),简称为xCSA方法[48].最近笔者提出一种测量蛋白质氨基1H CSA的脉冲序列,序列结合xCSA与NCO相关谱,即3D 1H xCSA脉冲序列[14](如图 8所示).序列中存在(8n–1)个π脉冲,持续时间为4n个转子周期,CSA放大倍数κ=6n.
|
图 8 (a) 基本xCSA放大单元;(b) 2D放大倍数κ = 6 xCSA放大实验脉冲序列与相干路径转移;(c)测量蛋白质氨基1H CSA的3D NCO/xCSA脉冲序列,即3D 1H xCSA脉冲序列.13C的载波频率设定为13CO频率范围,来得到NCO相关谱图,实心矩形框代表π/2脉冲,空心矩形框代表π脉冲.t1演化期间能够产生携带1H CSA信息的旋转边带强度信息.图与说明出自文献[14] Figure 8 (a) Basic xCSA amplification unit that can be inserted at the positions shown by red arrows for additional CSA amplification; (b) Pulse sequence and coherence transfer pathway for the 2D κ = 6 xCSA amplification experiment; (c) 3D NCO/xCSA pulse sequence for measurement of amide proton CSA. In fig. (c), the 13C carrier frequency is set to obtain NCO correlation. Narrow solid and empty rectangles in the pulse sequence denote π/2 and π-pulses, respectively. The figure and caption reproduced from reference [14] |
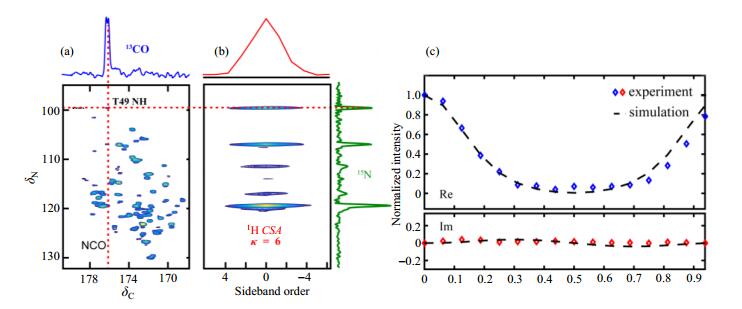
本文作者使用3D 1H xCSA方法测量部分氘代U-13C-15N-GB1蛋白的氨基1H CSA,通过图 8脉冲序列,可以得到1H CSA的旋转边带的演化,通过Matlab程序拟合谱图数据便可得到各残基位点1H CSA参数.研究中使用部分氘代样品,目的是为显著提高GB1氨基1H核的T2.图 9(a)与9(b)分别为3D 1H xCSA实验得到的NCO平面与1H xCSA平面,图中标记出残基位点为T49.
|
图 9 (a) [40%-HN, 2H, 13C, 15N] GB1微晶样品的3D 1H xCSA谱NCO平面与(b) T49氨基1H CSA平面.实验在Bruker Avance I 800谱仪上进行,魔角旋转转速为16 kHz,一个转子周期有16个t1增量,xCSA放大倍数为6;(c)一个转子周期之间的GB1残基V21氨基质子的实部与虚部t1时域信号.图与说明出自文献[14] Figure 9 (a) The 13C-15N NCO spectrum extracted from 3D xCSA experiment of for [40%-HN, 2H, 13C, 15N] GB1; (b) The 15N/ 1H CSA sideband intensities plane of T49. The spectrum was acquired at 800 MHz and 16 kHz MAS, with 16 t1 points spanning one rotor period and an amplification factor of κ = 6. (c) Experimental real and imaginary parts and respective fits of the t1 time-domain signal showing CSA evolution for the amide proton of residue V21 of GB1. The figure and caption reproduced from reference [14] |
液体NMR中,Hα、Cα、Cβ与CO位点的各向同性化学位移值经常被用来预测蛋白质的二级结构[49-51],然而,由于1H CSA数据量稀缺,研究者还没有通过实验观察到1H CSA张量与蛋白质二级结构的关系,对于CAP-Gly蛋白来说,其二级结构无α-螺旋结构,只存在β-折叠与无规卷曲,报道中没有进行1H CSA张量与蛋白质二级结构关系的探究[8].GB1蛋白的微晶结构已被知晓[52]:包含4条β-折叠和1条α-螺旋,其余为无规卷曲结构.从xCSA数据分析发现GB1 1H CSA张量对β-折叠结构更加敏感.β-折叠的CSA张量各组分平均值(δ11、δ22、δ33)高于α-螺旋与无规卷曲0.9、0.6与0.2,而α-螺旋与无规卷曲的差异则可以忽略.另外β-折叠的δ11分量大部分均大于17.4,而α-螺旋与无规卷曲部分则是相对随机的分布在17.4两侧[如图 10(b)所示].因此1H CSA张量可能作为蛋白质二级结构β-折叠的一个表征手段,但由于目前蛋白质1H CSA数据量较少,所以此结论还需更多数据支持.

|
图 10 (a) xCSA测量得到GB1蛋白氨基1H CSA三个张量δ11、δ22与δ33,灰色条状代表误差;(b) GB1蛋白氨基1H CSA张量(δ11 -17.4)与其二级结构、残基关系柱状图.紫色代表α-螺旋,红色代表β-折叠,绿色代表无规卷曲.图与说明出自文献[14] Figure 10 (a) Average 1H δ11, δ22 and δ33 values measured for the α-helix (purple), β-sheet (red) and random coil (green) segments of GB1. (b) A bar graph comparing GB1 1H CSA tensor (δ11 -17.4) with its secondary structure and residue number. The figure and caption reproduced from reference [14] |
表 1为本节中提到典型1H CSA测量方法或脉冲序列中所用样品、魔角旋转转速、化学位移各向异性重耦与1H-1H去耦方法、方法适用性与方法局限性总结.我们发现目前研究方向主要分两类:一是在超快魔角旋转条件下进行1H-1H同核去耦,同时使用对称脉冲重耦化学位移各向异性,虽然目前该方法多用于小分子体系,但随着转速越来越高,结合氘代样品,1H各项同性化学位移的分辨率会更好,将来完全有希望应用于大分子体系;另一个研究方向为快速魔角旋转条件下,将对称重耦脉冲或xCSA放大脉冲与3D 15N/13C相关实验相结合,达到更好的1H位点分辨率,该方法可以用于蛋白质等大分子体系.
| 表 1 本节提到测量1H CSA典型方法或脉冲序列归纳汇总 Table 1 The summary of all the typical methods or pulse sequences for measuring 1H CSA mentioned in this paper |
1H CSA的测量一直是NMR波谱学的研究重点,十几年来取得了重大进展.从魔角旋转转速的角度来说,分为静态、慢速魔角旋转、中速魔角旋转与超快魔角旋转实验;从研究对象来说,分为单晶、小分子、多肽与蛋白质等;从NMR实验维度来说,从一维实验,到二维实验,再发展到三维NMR实验;从方法上可分为粉末线型拟合,慢速旋转边带拟合、对称RNnv重耦方法与xCSA方法.这些变化取决于脉冲序列技术与核磁谱仪硬件的发展与进步.量子化学计算1H CSA的能力也随着近年计算机硬件迅猛发展,从而能够计算更加复杂的结构.
虽然研究者已经提出了如此多的方法,但1H CSA数据量依然较少,未来仍需发展更多技术与方法来测量1H CSA,尤其是蛋白质1H CSA的测量.文献中报道的1H CSA与氢键长度、角度及蛋白质二级结构的关系,希望将来会有更多实验与理论来支持.由于蛋白质氨基质子直接参与氢键形成,所以目前氨基1H CSA的测量仍占绝大多数,然而RNnv型脉冲分别与xCSA脉冲分别均可以不受限制的应用于其它体系,只需该体系中质子周围具有其它能够进行交叉极化的原子核(13C、31P、15N等核),所以未来结合更高磁场,部分氘代样品等手段,完全可以测量蛋白质Hα与Hβ等1H CSA.
| [1] | WYLIE B J, RIENSTRA C M. Multidimensional solid state NMR of anisotropic interactions in peptides and proteins[J]. J Chem Phys, 2008, 128(5): 052207. DOI: 10.1063/1.2834735. |
| [2] | FACELLI J C. Chemical shift tensors:Theory and application to molecular structural problems[J]. Prog Nucl Mag Res Sp, 2011, 58(3, 4): 176-201. |
| [3] | SAITO H, ANDO I, RAMAMOORTHY A. Chemical shift tensor-the heart of NMR:Insights into biological aspects of proteins[J]. Prog Nucl Mag Res Sp, 2010, 57(2): 181-228. DOI: 10.1016/j.pnmrs.2010.04.005. |
| [4] | BAX A, SZEVERENYI N M, MACIEL G E. Correlation of isotropic shifts and chemical-shift anisotropies by two-dimensional fourier-transform magic-angle hopping NMR-spectroscopy[J]. J Magn Reson, 1983, 52(1): 147-152. |
| [5] | LOTH K, PELUPESSY P, BODENHAUSEN G. Chemical shift anisotropy tensors of carbonyl, nitrogen, and amide proton nuclei in proteins through cross-correlated relaxation in NMR spectroscopy[J]. J Am Chem Soc, 2005, 127(16): 6062-6068. DOI: 10.1021/ja042863o. |
| [6] | BROUWER D H, RIPMEESTER J A. Symmetry-based recoupling of proton chemical shift anisotropies in ultrahigh-field solid-state NMR[J]. J Magn Reson, 2007, 185(1): 173-178. DOI: 10.1016/j.jmr.2006.12.003. |
| [7] | YAO L, GRISHAEV A, CORNILESCU G, et al. The impact of hydrogen bonding on amide 1H chemical shift anisotropy studied by cross-correlated relaxation and liquid crystal NMR spectroscopy[J]. J Am Chem Soc, 2010, 132(31): 10866-10875. DOI: 10.1021/ja103629e. |
| [8] | HOU G J, PARAMASIVAM S, YAN S, et al. Multidimensional magic angle spinning NMR spectroscopy for site-resolved measurement of proton chemical shift anisotropy in biological solids[J]. J Am Chem Soc, 2013, 135(4): 1358-1368. DOI: 10.1021/ja3084972. |
| [9] | KOVER K E, BATTA G, HRUBY V J. Solution-phase chemical shift anisotropy as a promising tool to probe intermolecular interactions and peptide bond geometry:a case study on 15N-labeled Nα-t-Boc-L-valine[J]. Magn Reson Chem, 2003, 41(10): 828-836. DOI: 10.1002/mrc.v41:10. |
| [10] | TESSARI M, MULDER F A A, BOELENS R, et al. Determination of amide proton CSA in 15N-labeled proteins using 1H CSA/15N-1H dipolar and 15N CSA/15N-1H dipolar cross-correlation rates[J]. J Magn Reson, 1997, 127(1): 128-133. DOI: 10.1006/jmre.1997.1199. |
| [11] | TJANDRA N, BAX A. Solution NMR measurement of amide proton chemical shift anisotropy in 15N-enriched proteins. correlation with hydrogen bond length[J]. J Am Chem Soc, 1997, 119(34): 8076-8082. DOI: 10.1021/ja970876e. |
| [12] | CORNILESCU G, BAX A. Measurement of proton, nitrogen, and carbonyl chemical shielding anisotropies in a protein dissolved in a dilute liquid crystalline phase[J]. J Am Chem Soc, 2000, 122(41): 10143-10154. DOI: 10.1021/ja0016194. |
| [13] | BERGLUND B, VAUGHAN R W. Correlations between proton chemical shift tensors, deuterium quadrupole couplings, and bond distances for hydrogen bonds in solids[J]. J Chem Phys, 1980, 73(5): 2037-2043. DOI: 10.1063/1.440423. |
| [14] | GE Y W, HUNG I, LIU X L, et al. Measurement of amide proton chemical shift anisotropy in perdeuterated proteins using CSA amplification[J]. J Magn Reson, 2017, 284: 33-38. DOI: 10.1016/j.jmr.2017.09.009. |
| [15] | HADDIX D C, LAUTERBUR C C. Molecular dynamics and structure of solids[J]. Natl Bur Stand, 1969: 403-406. |
| [16] | MOROZ N K, PANICH A M, GABUDA S P. Shielding anisotropy of H-bonded protons in Cs2GeF6·4HF[J]. J Magn Reson, 1969, 1983, 53(1): 1-6. |
| [17] | TEKELY P, PALMAS P, MUTZENHARDT P. Influence of proton chemical-shift anisotropy on magic-angle spinning spectra of hydrate crystals[J]. J Magn Reson, 1997, 127(2): 238-240. DOI: 10.1006/jmre.1997.1209. |
| [18] | IWAMIYA J H, SINTON S W, LIU H, et al. Multiple-pulse sequences for homonuclear decoupling[J]. J Magn Reson, 1969, 1992, 100(2): 367-375. |
| [19] | HU J Z, ALDERMAN D W, YE C H, et al. An isotropic chemical shift-chemical shift anisotropy magic-angle slow-spinning 2D NMR experiment[J]. J Magn Reson Ser A, 1993, 105(1): 82-87. DOI: 10.1006/jmra.1993.1252. |
| [20] | HOHWY M, RASMUSSEN J T, BOWER P V, et al. 1H chemical shielding anisotropies from polycrystalline powders using MSHOT-3 based CRAMPS[J]. J Magn Reson, 1998, 133(2): 374-378. DOI: 10.1006/jmre.1998.1449. |
| [21] | PINES A, VEGA S, MEHRING M. NMR double quantum spin decoupling in solids[J]. Phys Rev, 2011, 18(1): 112-125. |
| [22] | PINES A, RUBEN D J, VEGA S, et al. New approach to high-resolution proton NMR in solids:deuterium spin decoupling by multiple-quantum transitions[J]. Phys Rev Lett, 1976, 36(36): 110-113. |
| [23] | VEGA S, SHATTUCK T W, PINES A. Fourier-transform double-quantum NMR in solids[J]. Phys Rev Lett, 1976, 37(1): 43-46. DOI: 10.1103/PhysRevLett.37.43. |
| [24] | ACHLAMA A M. The chemical shift and EFG tensors at the carboxylic deuterons of α-oxalic acid dihydrate[J]. J Magn Reson, 1980, 41(3): 374-380. |
| [25] | ACHLAMA A M. The chemical shift, dipolar, and quadrupolar tensors of deuterium in potassium bicarbonate[J]. J Chem Phys, 1981, 74(6): 3623-3625. DOI: 10.1063/1.441472. |
| [26] | REX GERALD I I, BERNHARD T, HAEBERLEN U, et al. Chemical shift and electric field gradient tensors for the amide and carboxyl hydrogens in the model peptide N-acetyl-D, L-valine. Single-crystal deuterium NMR study[J]. J Am Chem Soc, 1993, 115(2): 777-782. DOI: 10.1021/ja00055a058. |
| [27] | DUMA L, ABERGEL D, TEKELY P, et al. Proton chemical shift anisotropy measurements of hydrogen-bonded functional groups by fast magic-angle spinning solid-state NMR spectroscopy[J]. Chem Commun, 2008, 20: 2361-2363. |
| [28] | PANDEY M K, YARAVA J R, ZHANG R, et al. Proton-detected 3D 15N/1H/1H isotropic/anisotropic/isotropic chemical shift correlation solid-state NMR at 70 kHz MAS[J]. Solid State Nucl Magn Reson, 2016, 76-77: 1-6. DOI: 10.1016/j.ssnmr.2016.03.001. |
| [29] | ZHANG R, MROUE K H, RAMAMOORTHY A. Proton-based ultrafast magic angle spinning solid-state NMR spectroscopy[J]. Acc Chem Res, 2017, 50(4): 1105-1113. DOI: 10.1021/acs.accounts.7b00082. |
| [30] | HOU G, GUPTA R, POLENOVA T, et al. A magic-angle spinning NMR method for the site-specific measurement of proton chemical-shift anisotropy in biological and organic solids[J]. Isr J Chem, 2014, 54(1, 2): 171-183. |
| [31] | MOON S, CASE D A. A new model for chemical shifts of amide hydrogens in proteins[J]. J Biomol NMR, 2007, 38(2): 139-150. DOI: 10.1007/s10858-007-9156-8. |
| [32] | OSAPAY K, CASE D A. A new analysis of proton chemical shifts in proteins[J]. J Am Chem Soc, 1991, 113(25): 9436-9444. DOI: 10.1021/ja00025a002. |
| [33] | OSAPAY K, CASE D A. Analysis of proton chemical shifts in regular secondary structure of proteins[J]. J Biomol NMR, 1994, 4(2): 215-230. |
| [34] | SITKOFF D, CASE D A. Density functional calculations of proton chemical shifts in model peptides[J]. J Am Chem Soc, 1997, 119(50): 12262-12273. DOI: 10.1021/ja9721430. |
| [35] | DEJAEGERE A, BRYCE R A, CASE D A. An empirical analysis of proton chemical shifts in nucleic acids[J]. Acs Symposium, 1999, 732: 194-206. DOI: 10.1021/symposium. |
| [36] | TANG S, CASE D A. Calculation of chemical shift anisotropy in proteins[J]. J Biomol NMR, 2011, 51(3): 303-312. DOI: 10.1007/s10858-011-9556-7. |
| [37] | SHARMA Y, KWON O Y, BROOKS B, et al. An ab initio study of amide proton shift tensor dependence on local protein structure[J]. J Am Chem Soc, 2002, 124(2): 327-335. DOI: 10.1021/ja016859d. |
| [38] | PARKER L L, HOUK A R, JENSEN J H. Cooperative hydrogen bonding effects are key determinants of backbone amide proton chemical shifts in proteins[J]. J Am Chem Soc, 2006, 128(30): 9863-9872. DOI: 10.1021/ja0617901. |
| [39] | SUZUKI Y, TAKAHASHI R, SHIMIZU T, et al. Intra-and intermolecular effects on 1H chemical shifts in a silk model peptide determined by high-field solid state 1H NMR and empirical calculations[J]. J Phys Chem B, 2009, 113(29): 9756-9761. DOI: 10.1021/jp903020p. |
| [40] | MIAH H K, BENNETT D A, IUGA D, et al. Measuring proton shift tensors with ultrafast MAS NMR[J]. J Magn Reson, 2013, 235(Supplement C): 1-5. |
| [41] | PANDEY M K, NISHIYAMA Y. Determination of NH proton chemical shift anisotropy with 14N-1H heteronuclear decoupling using ultrafast magic angle spinning solid-state NMR[J]. J Magn Reson, 2015, 261: 133-140. DOI: 10.1016/j.jmr.2015.10.015. |
| [42] | PANDEY M K, MALON M, RAMAMOORTHY A, et al. Composite-180° pulse-based symmetry sequences to recouple proton chemical shift anisotropy tensors under ultrafast MAS solid-state NMR spectroscopy[J]. J Magn Reson, 2015, 250(Supplement C): 45-54. |
| [43] | PANDEY M K, NISHIYAMA Y. Determination of relative orientation between 1H CSA tensors from a 3D solid-state NMR experiment mediated through 1H/1H RFDR mixing under ultrafast MAS[J]. Solid State Nucl Magn Reson, 2015, 70(Supplement C): 15-20. |
| [44] | CARRAVETTA M, EDEN M, ZHAO X, et al. Symmetry principles for the design of radiofrequency pulse sequences in the nuclear magnetic resonance of rotating solids[J]. Chem Phys Lett, 2000, 321(3, 4): 205-215. |
| [45] | ZHAO X, EDEN M, LEVITT M H. Recoupling of heteronuclear dipolar interactions in solid-state NMR using symmetry-based pulse sequences[J]. Chem Phys Lett, 2001, 342(3): 353-361. |
| [46] | GULLION T. Extended Chemical-Shift Modulation[J]. J Magn Reson, 1989, 85(3): 614-619. |
| [47] | RALEIGH D P, KOLBERT A C, OAS T G, et al. Enhancement of the effect of small anisotropies in magic-angle spinning nuclear magnetic resonance[J]. J Chem Soc, Faraday Trans, 1988, 84(11): 3691-3711. DOI: 10.1039/f19888403691. |
| [48] | HUNG I, GAN Z. An efficient amplification pulse sequence for measuring chemical shift anisotropy under fast magic-angle spinning[J]. J Magn Reson, 2011, 213(1): 196-199. DOI: 10.1016/j.jmr.2011.09.015. |
| [49] | WISHART D S, SYKES B D, RICHARDS F M. The chemical shift index:a fast and simple method for the assignment of protein secondary structure through NMR spectroscopy[J]. Biochemistry, 1992, 31(6): 1647-1651. DOI: 10.1021/bi00121a010. |
| [50] | WISHART D S, SYKES B D. [12] Chemical shifts as a tool for structure determination[J]. Methods Enzymol, 1994, 239: 363-392. DOI: 10.1016/S0076-6879(94)39014-2. |
| [51] | WISHART D, SYKES B D. The 13C Chemical-shift index:a simple method for the identification of protein secondary structure using 13C chemical-shift data[J]. J Biomol NMR, 1994, 4(2): 171-180. |
| [52] | ANDREAS L B, JAUDZEMS K, STANEK J, et al. Structure of fully protonated proteins by proton-detected magic-angle spinning NMR[J]. Proc Natl Acad Sci U S A, 2016, 113(33): 9187-9192. DOI: 10.1073/pnas.1602248113. |
 2018, Vol. 35
2018, Vol. 35 
