2. 重庆师范大学 物理与电子工程学院, 重庆 401331
2. School of Physics and Electronic Engineering, Chongqing Normal University, Chongqing 401331, China
核磁共振(NMR)技术在工程现场的应用一直是研究者们努力实现的方向.目前,NMR已在石油测井[1]和电力橡胶绝缘材料老化检测[2, 3]方面显现出较好的实用价值.但便携性NMR仪器的磁场很难达到很高的场强和均匀度,而且受现场复杂工况(比如石油测井中的仪器振动和极端的温度、压力)的影响,NMR信号信噪比相对较低.通常通过增加重复测量次数来提升信噪比,这就意味着需要较多的测量时间,因此对于现场NMR技术来说,提高测量效率显得格外重要.要提高测量效率,测量参数的合理设置是关键.然而,目前参数设置主要依靠操作人员依经验进行多次尝试后,最终设置一个比较合适的值.这种做法费时,且对操作人员素质要求比较高.下面以自扩散系数(D0)和纵向弛豫时间(T1)测量为例,进行详细说明.
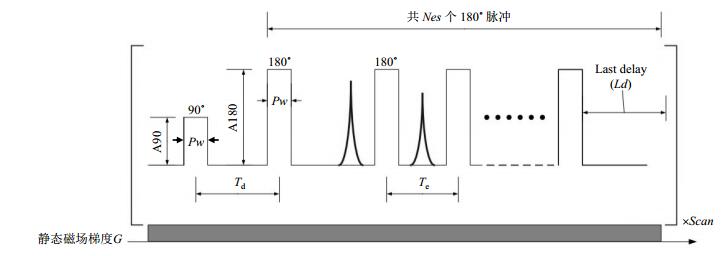
图 1是低场NMR中,当静态梯度磁场存在时,测量D0的SGSE序列[4].其中90˚脉冲与180˚脉冲的时间间隔(Td)是可变的.在测量扩散特性时,我们逐渐增大Td,并以Td为横坐标、每个Td对应的CPMG回波信号前若干个回波信号的峰值和为纵坐标(带有测量误差),可以拟合出梯度磁场下液体分子的扩散衰减曲线(图 2),从而求出作为曲线参变量的D0.为了提高回波信号峰值的信噪比,需要重复图 1所示序列若干次并进行叠加,因此相当耗时.
|
图 1 SGSE测量序列 Figure 1 SGSE sequence |
目前实现“增大Td值”的方式是均匀步进,即设置Td的“起点值”、“终点值”、“步进数”:(1)Td的起点值Td Min是90˚脉冲与第一个180˚脉冲之间的时间间隔最小值,单位为μs;(2)Td的终点值Td Max是90˚脉冲与第一个180˚脉冲之间的时间间隔最大值,单位为μs;(3)扩散加权时间Td的扫描步进数Steps是Td Min和Td Max之间细分的扫描测量步进数目.
要想测量准确,就要根据样品的扩散曲线设置相适应的Td Min、Steps、Td Max三个参数.实际上面对一个新样品时,测量人员对其扩散曲线是未知的,因此需要不断的改变Td Min、Steps、Td Max,去进行多次试测,用这些试测值来大致估计样品的扩散曲线,这种试测无疑会消耗大量时间.同时,大部分测量仪器使用者并不具有测量原理相关的背景知识,很难根据测试值作出针对性的参数调整,甚至根本无法完成测量.因此将测量过程自动化,不仅能节约测量时间、提高测量效率,还能降低测量门槛,有利于NMR测量的推广.
近些年人工智能发展迅速,广泛应用于工业自动化领域,本文介绍了一种基于蒙特卡罗算法的NMR参数智能搜索方法,可以实现T1、D0测量中关键参数的自动设置.通过上述介绍我们知道,测量自动化的关键在于通过算法估计真实的扩散曲线,蒙特卡罗模拟则可以有效解决该问题.
1 算法介绍 1.1 蒙特卡罗方法简介蒙特卡罗方法(Monte Carlo Method),也称统计模拟方法,是20世纪40年代中期由于科学技术的发展和电子计算机的发明,而提出的一种以概率统计理论为指导的数值计算方法.蒙特卡罗并不指某一具体算法,而是一类随机方法的统称.这种方法的特点是可以通过对随机采样的计算得到近似结果,随机采样越多,得到的结果越近似最优解,但无论采样多少次它一定能返回一个结果[5].与之对应的另一类随机算法称为拉斯维加斯算法,它的特点是采样越多越有可能找到最优解,但不保证能返回这个最优解.我们通过蒙特卡罗模拟随机生成大量扩散曲线,再根据已知的测量数据排除掉不合理的扩散曲线,剩下的曲线集合就可以用于估计真实扩散曲线.
1.2 蒙特卡罗算法数学模型前文提到目前我们一般是通过设定Td的“起点、终点、步进数”来不断等间距改变Td值,所以参数设置的自动化实际就是Td值选择的自动化.本文期望机器能根据已有的测量数据自动选择最优的Td值,同时不再拘泥于等间距改变Td.
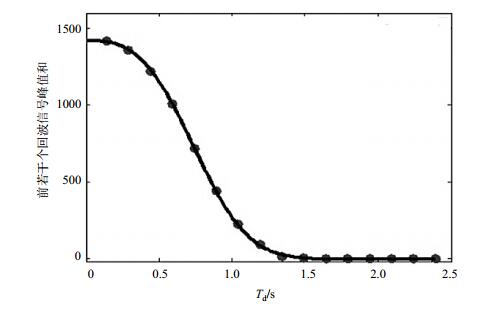
假设如图 2所示的任意测量曲线为:
| $ y = f(t) $ | (1) |
|
图 2 梯度磁场下液体分子的扩散衰减曲线 Figure 2 Diffusion decay curve of liquid in gradient magnetic field |
t是测量数据点的横坐标Td,单位为ms;y是纵坐标,代表归一化回波幅值.
| $ err \sim N(0, {\sigma ^2}) $ | (2) |
对
| $ \sum\limits_{i = 1}^N {{{[{{\dot y}_i} - {f_{{\mathit{\boldsymbol{A}}_k}}}({{\dot t}_i})]}^2} < N} {\sigma ^2} $ | (3) |
则认为该参数
对一个纵坐标t,参数向量取
| $ \left\{ \begin{array}{l} E{Y_t} = \sum\limits_{i = 1}^N {{y_{i, t}}/N} \\ D{Y_t} = \sum\limits_{i = 1}^N {{{({a_i} - E{Y_t})}^2}/N} \end{array} \right. $ | (4) |
| $ \hat y = E{Y_t} $ | (5) |
同时方差
| $ {\dot t_{i + 1}} = t|D{Y_t} = {\rm{Max}}(D{Y_t}) $ | (6) |
一般样品的T1在1 ms以上,可取测量初始点t1=1 ms.值得注意的是,初始点的选择对最终结果影响不大,算法会自动根据初始点返回的结果进行后续测量.
每更新一个测量点我们就做一次拟合,求得关键参数
| $ |{\hat a_{0(i)}} - {\hat a_{0(i - 1)}}| < \varepsilon $ | (7) |
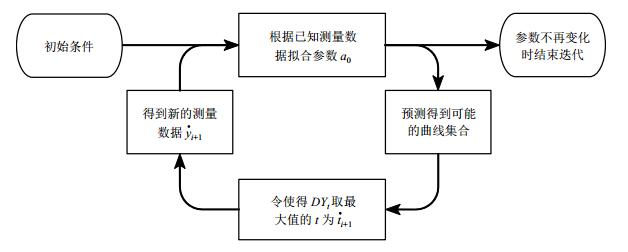
整个算法流程可用图 3表示.
|
图 3 算法流程图 Figure 3 Algorithm flowchart |
以下,本文将分析两种最常用的测量情景.
1.2.1 D0测量测量D0曲线时,
| $ f(t) = B*{{\rm{e}}^{ - {{(\frac{t}{{{D_0}}})}^3}}} $ | (8) |
此时参数向量A=[D0,
B].考虑到(8)式的形式,若不存在测量误差时,B应等于实测回波峰值和的最大值
| $ \left\{ \begin{array}{l} {D_0} \sim U[0, {10^{ - 8}}]\\ B \sim U[{\rm{Max}}({{\dot y}_i}) - 5\sigma , {\rm{Max}}({{\dot y}_i}) + 5\sigma ] \end{array} \right. $ | (9) |
按上述分布进行多次随机抽样,当满足
| $ {\sum\limits_{i = 1}^N {\left[ {{{\dot y}_i} - B*{{\rm{e}}^{ - {{(\frac{t}{{{D_0}}})}^3}}}} \right]} ^2} < N{\sigma ^2} $ | (10) |
条件的曲线足够多时,可计算
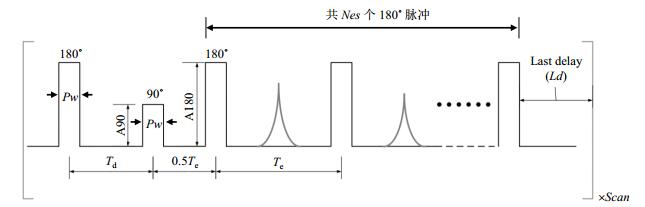
测量T1使用的IR序列如图 4所示.与SGSE序列类似,IR序列中的Td值也是可变的.我们通过设置“Td Min、Td Steps、Td Max”三个参数来不断增大T1,重复该序列“Scan”次.
|
图 4 IR序列 Figure 4 IR sequence |
测量T1曲线时,
| $ f(t) = C*{{\rm{e}}^{ - t/{T_1}}} $ | (11) |
常见样品的T1在0~5 000 ms范围内,可设T1、C服从分布:
| $ \left\{ \begin{array}{l} {T_1} \sim U[0, 5\, {\kern 1pt} 000]\\ C \sim U[{\rm{Max}}({{\dot y}_i}) - 5\sigma , {\rm{Max}}({{\dot y}_i}) + 5\sigma ] \end{array} \right. $ | (12) |
按上述分布进行多次随机抽样,从中筛选出满足下式的曲线计算
| $ \sum\limits_{i = 1}^N ( {\dot y_i} - C*{{\rm{e}}^{ - t/{T_1}}}{)^2} < N{\sigma ^2} $ | (13) |
将计算得到的
为了验证上述算法的有效性,我们用该算法取点测量纯水的扩散系数D0和T1.将算法得出的

|
图 5 测量流程图 Figure 5 Measurement flowchart |
设定误差上限ε= 10-10,测量12个点后算法停止迭代.随着测量数据增加,预测数据集不断减小,给出已知数据分别为1、5、8、12个时候的预测数据集如图 6所示.实测数据绘出的扩散曲线如图 7所示,最终拟合得到D0 = 2.447×10-9 cm2·s-1.

|
图 6 D0测量中预测数据集随测量数据增加的收敛情况 Figure 6 Convergence of predicted data sets with increasing measured data in D0 measurement |
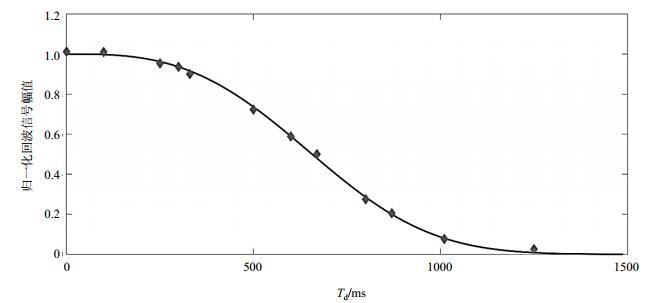
|
图 7 纯水实测扩散曲线 Figure 7 Diffusion measurement curve of pure water |
使用同样的算法测量纯水的T1,设定误差上限ε= 1,测量13个点后算法停止迭代.已知数据个数分别为1、5、8、13时候的预测数据集如图 8所示.测出T1曲线如图 9所示,拟合得到T1=2 754.1 ms.
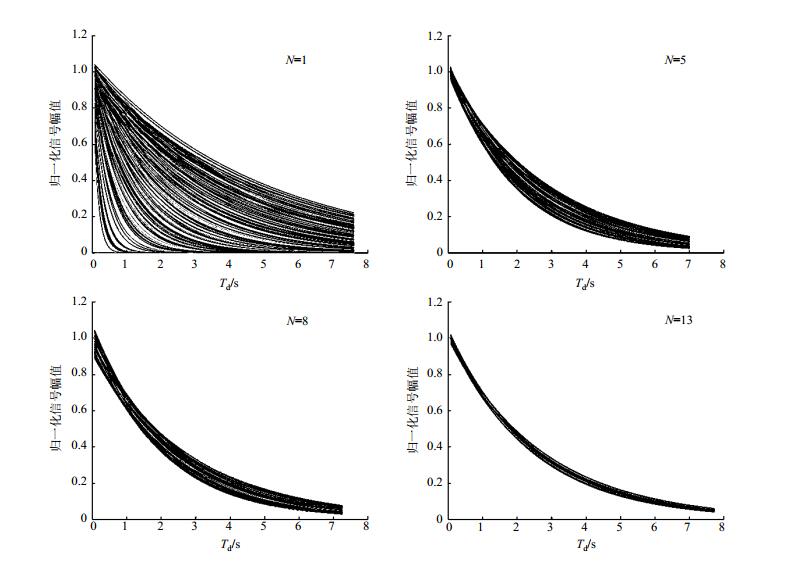
|
图 8 T1测量中预测数据集随测量数据增加的收敛情况 Figure 8 Convergence of predicted data sets with increasing measured data in T1 measurements |

|
图 9 纯水实测T1曲线 Figure 9 T1 measurement curve of pure water |
考虑到温度影响,可以认为该算法下测得的纯水的D0、T1参数基本准确.
3 结论本文通过蒙特卡罗模拟对样品的扩散和弛豫曲线进行估计,算法根据估计值选取最优测量参数,实现了D0、T1测量时参数设置的自动化,节省测量时间的同时还大幅降低了测量门槛,利于NMR技术的推广.经验证该算法能够得到较为准确的测量结果.值得注意的是,本文所提的人工智能搜索算法是建立在单一组分样品的前提下,要想适用于多组分样品还需要对上述算法进行扩展,这也是本团队后继的研究方向.
致谢 作者徐征感谢与Schlumberger公司宋一桥博士的讨论,以及宋一桥博士在思路上提供的帮助.| [1] | 肖立志. 井下极端环境核磁共振科学仪器[M]. 北京: 科学出版社, 2016. |
| [2] |
XU Z, WU J M. A portable unilateral nuclear magnetic resonance sensor used for detecting the aging status of composite insulator[J].
Transactions of China Electrotechnical Society., 2016, 31(12): 118-125.
徐征, 吴嘉敏. 用于复合绝缘子伞裙老化状态检测的单边核磁共振传感器[J]. 电工技术学报, 2016, 31(12): 118-125. DOI: 10.3969/j.issn.1000-6753.2016.12.014. |
| [3] | XU Z, CUI X J, MENG K K, et al. Novel unilateral NMR sensor for assessing the aging status of silicone rubber insulator[J]. IEEE Sens J, 2016, 16(5): 1168-1175. |
| [4] | RATA D G, CASANOVA F, PERLO J, et al. Self-diffusion measurement by a mobile single-sided NMR sensor with improved magnetic field gradient[J]. J Magn Reson, 2006, 180(2): 229-235. DOI: 10.1016/j.jmr.2006.02.015. |
| [5] | 康崇禄. 蒙特卡罗方法理论和应用[M]. 北京: 科学出版社, 2015. |
| [6] | 杨虎, 刘琼荪, 钟波. 概率论与数理统计[M]. 重庆: 重庆大学出版社, 2007. |
| [7] | SONG Y Q. A machine learning based adaptive method for multi-parametric NMR experiments[C]. Halifax: 14th ICMRM. 2017. |
 2018, Vol. 35
2018, Vol. 35 
