磁共振成像(Magnetic Resonance Imaging,MRI)能够看到人体内部组织的断层扫描图像,由于该技术具有较高的分辨率、对人体无损伤等优点,因此被广泛的应用到医学检测中,为病变的早期发现和诊断提供了坚实的依据.
谱仪是MRI系统中的核心设备,主要功能是控制系统的时序、发射射频脉冲、产生梯度信号以及接收回波信号等[1-4].其中梯度模块是谱仪的重要组成部分之一,负责发出选层、频率编码以及相位编码三个通道的梯度波形,驱动X、Y、Z三个方向的梯度线圈产生梯度磁场.在梯度磁场的发生过程中,由于涡流效应,它们分别会对主磁场B0产生影响,在B0上叠加指数衰减项.这会使得重建后的图像产生形变、伪影等现象[5],必须在成像系统中对其进行涡流补偿,所以消除涡流是MRI系统保证成像质量的关键之一.
涡流补偿的方法主要有两种:一种是由Mansfield和Chapman共同提出的自屏蔽梯度线圈的方法[5],消除线圈与主磁体之间的相互作用,这种方法需要对梯度线圈进行重新设计,成本较高.另外一种方法就是对梯度电流进行预补偿,以弥补磁场受涡流效应的影响[6-10].现有技术只对梯度在自身方向上产生的涡流效应进行了分析和补偿,而没有考虑梯度对静磁场B0的影响.而事实上,三个方向上的梯度磁场除了会在各种方向上产生涡流,也会共同影响主磁场B0的稳定性,从而影响成像质量[11],因而有必要针对B0场的涡流效应进行预补偿.
本文设计了一种基于现场可编程门阵列(Field Programmable Gate Array, FPGA)的预补偿的方法,以产生B0信号,补偿三个方向的梯度磁场对B0产生的涡流影响.FPGA具有很好的并行性,可以同时计算三个方向的梯度对B0的影响,有较高的运算效率.另外,由于难以通过示波器观测并判断B0信号是否准确,需要再通过高速采集卡采集B0(采样率为2 MHz),对采样结果进行最小二乘拟合以检验结果是否准确.本文设计的B0高精度发生方法,弥补了谱仪在梯度发生上的空缺.
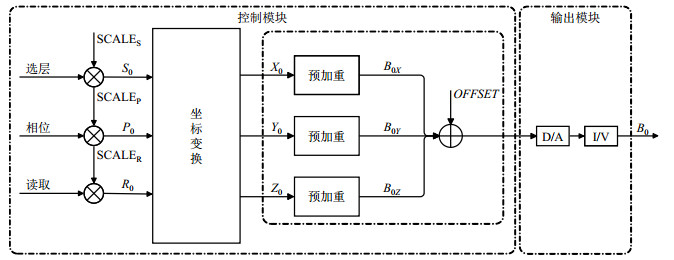
1 B0计算的FPGA实现谱仪采用FPGA器件实现梯度发生的实时计算.在FPGA中,B0发生的结构框图如图 1所示.根据外部的参数配置,在FPGA上实现数据的读取、缩放、坐标转换和预加重的功能.数字波形的处理结果发送到数模转换器(D/A)的梯度输出模块,经电流/电压转换器(I/V)之后用于采集.
|
图 1 梯度计算中B0的发生框图 Figure 1 A block diagram of B0 occurrence in gradient computation |
B0的计算如(1)~(4)式所示:
| $ {B_0}(t) = \sum\limits_{i = 1}^N {p_X^i(t) + } \sum\limits_{i = 1}^N {p_Y^i(t) + } \sum\limits_{i = 1}^N {p_Z^i(t) + OFFSET} $ | (1) |
| $ p_X^i(t) = a_X^i \cdot \frac{{{\rm{d}}{X_0}(t)}}{{{\rm{d}}t}} - b_X^i \cdot \frac{{{\rm{d}}p_X^i(t)}}{{{\rm{d}}t}},\ \ i = 1, 2, 3, 4 $ | (2) |
| $ p_Y^i(t) = a_Y^i \cdot \frac{{{\rm{d}}{Y_0}(t)}}{{{\rm{d}}t}} - b_Y^i \cdot \frac{{{\rm{d}}p_Y^i(t)}}{{{\rm{d}}t}}, \ \ i = 1, 2, 3, 4 $ | (3) |
| $ p_Z^i(t) = a_Z^i \cdot \frac{{{\rm{d}}{Z_0}(t)}}{{{\rm{d}}t}} - b_Z^i \cdot \frac{{{\rm{d}}p_Z^i(t)}}{{{\rm{d}}t}}, \ \ i = 1, 2, 3, 4 $ | (4) |
其中N代表补偿项的数量,此处最大设为4.aXi、aYi、aZi和bXi、bYi、bZi分别代表X、Y、Z方向的幅度常数和时间常数,OFFSET为直流偏置.幅度常数aXi、aYi和aZi为16 bit有符号整数,时间常数bXi、bYi和bZi位32 bit有符号整数.X为选层方向,Y为相位编码方向,Z为读方向.X、Y、Z三个方向的预加重补偿是并行运算的.
用FPGA实现上述功能,需要先将微分方程转换成便于程序实现的差分方程形式.以(2)式为例,其差分方程转化过程如(5)~(8)式所示,其中n代表离散时间.
| $ p_X^i(n) = a_X^i \cdot [{X_0}(n) - {X_0}(n - 1)] - b_X^i \cdot [p_X^i(n) - p_X^i(n - 1)], \ \ \ i = 1, 2, 3, 4 $ | (5) |
| $ (1 + b_X^i) \cdot p_X^i(n) = a_X^i \cdot [{X_0}(n) - {X_0}(n - 1)] + b_X^i \cdot p_X^i(n - 1), \ \ \ i = 1, 2, 3, 4 $ | (6) |
| $ p_X^i(n) = \frac{{a_X^i}}{{1 + b_X^i}} \cdot [{X_0}(n) - {X_0}(n - 1) + \frac{{b_X^i}}{{a_X^i}} \cdot p_X^i(n - 1)], \ \ \ i = 1, 2, 3, 4 $ | (7) |
令
| $ p_X^i(n) = PREA_X^i \cdot [{X_0}(n) - {X_0}(n - 1) + PREK_X^i \cdot p_X^i(n - 1)], \ \ \ i = 1, 2, 3, 4 $ | (8) |
本文设计的选用的FPGA为Altera公司的EP3C55F484,它有55 856个逻辑单元以及156个硬件乘法器.逻辑框图如图 1所示,FPGA完成了梯度数据波形的读取、幅度的缩放、以及预加重的核心功能,并将处理后的结果发送到梯度输出模块的D/A.FPGA的并行架构和高速处理,可以让涡流补偿达到纳秒(ns)级的分辨率.FPGA的编程语言采用硬件描述语言(Hardware Description Language, VHDL),编译环境为Altera公司的Quartus Ⅱ.FPGA操作核心的时钟频率为50 MHz,将从数字信号处理器(Digital Signal Process, DSP)中读取到的波形数据基于变换矩阵进行坐标变换之后得到X、Y、Z方向的梯度数据,分别做预加重运算,得到三个方向对B0磁场的涡流影响B0X、B0Y和B0Z,将这三项与直流偏置项OFFSET叠加,得到B0的预补偿结果,最后经过输出模块的D/A和I/V将结果输出.
FPGA的程序采用三级流水操作.第一级流水实现梯度数据的读取、增益控制和梯度变换,第二级流水完成B0信号的预增强,是程序的核心部分,第三级流水实现波形数据的并串转换.为了达到实时性的要求,需要加快计算速度,本文采取了并行设计模式,对X、Y、Z三路的波形数据进行并行运算,再将三路并行的输出结果进行叠加.该方案依赖于FPGA丰富的硬件资源,包括硬件乘法器和高速时钟等.该方案具有较高的处理速度和较好的设计灵活性,满足B0补偿高速实时的要求.通过精心设计,B0波形的时间分辨率达到1 μs.
2 信号采集分别从X、Y、Z三个方向同步产生如图 2(a)~(c)所示的矩形信号,将经过补偿的B0信号输出到示波器观察输出波形,如图 2(d)所示.当输入波形的幅度较小,或者设置的幅度参数较小时,输出的B0信号幅度较小,会有较大的噪声,信噪比低,如图 2(e)所示.这种情况下,难以对B0进行观察和测量.为了更好的验证设计,测量B0的输出结果,并且与理论值进行比较,这里用高速采集卡对数据进行采集,以实现进一步的分析和验证.

|
图 2 (a) X方向的输入梯度;(b) Y方向的输入梯度;(c) Z方向的输入梯度;(d) B0输出结果;(e) 小幅度的B0信号 Figure 2 (a) Input gradient in X; (b) Input gradient in Y; (c) Input gradient in Z; (d) Output of B0; (e) Output of B0 with small amplitude |
本文选用ADLINK PCI-9846的高速采集卡,采样率为2 MHz,每个采样点的时间间隔为0.5 μs,经过数据采集卡采样得到的B0信号以双精度浮点格式存储,由谱仪输出的数字门控进行采集的触发.
3 采集结果的测试和分析涡流对B0的影响是一种近似多时间常数的指数衰减,用Matlab对采集到的信号进行最小二乘拟合,计算确定系数,以验证产生的B0信号的可信度.拟合曲线公式为(9)式,确定系数的计算为(10)式.
| $ {B_0}(t) = \sum\limits_{i = 1}^N {{k_i}} \cdot q_i^t + DC $ | (9) |
| $ {R^2} = \frac{{SSR}}{{SST}} = \frac{{{{\sum {({{\hat y}_i} - {{\bar y}_i})} }^2}}}{{{{\sum {({y_i} - {{\bar y}_i})} }^2}}} $ | (10) |
其中,N为添加的预加重参数的个数,ki为补偿结果的起始幅值,qi为衰减率,DC为直流偏置.
输入幅值为2.5 V的矩形波,对一个补偿项进行参数对比,拟合后的参数计算结果应该与设置的幅度常数a呈线性相关.设置的幅度常数a与起始幅值的理论值k理的对应关系如(11)式所示,其中amax为幅度常数的最大值,即0x7FFFFFFF,当amax = 0x7FFFFFFF时,对应的起始幅值kmax = -2.5.理论值与实验值的误差δ计算公式如(12)式所示,其中k为拟合得到的起始幅值.
| $ \frac{{{k_{\rm{理}}}}}{{{k_{\max }}}} = \frac{a}{{{a_{\max }}}} $ | (11) |
| $ {\delta _k} = \frac{{|k - {k_{\rm{理}}}|}}{{{k_{\rm{理}}}}} $ | (12) |
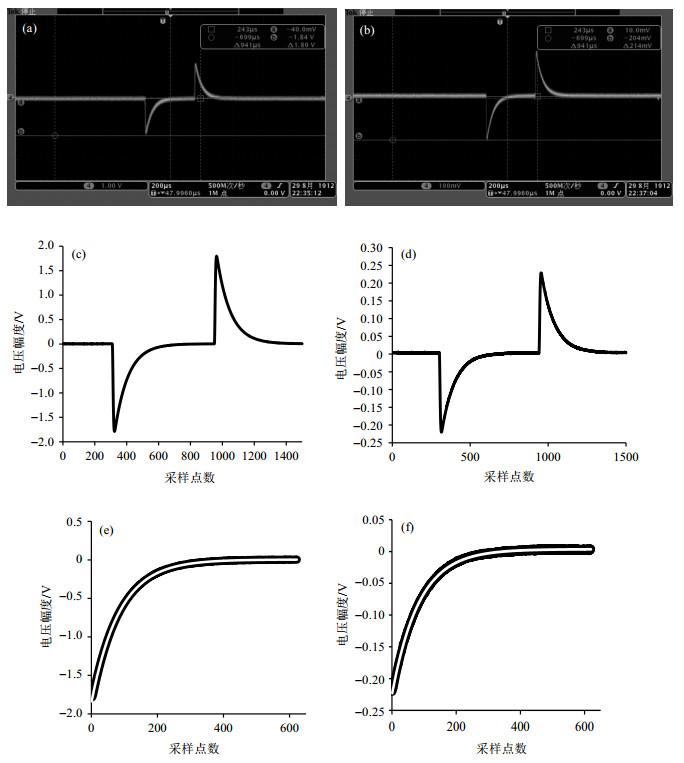
将时间常数设为固定值b= 0x7D00FFFF,幅度常数设置为a= 0x5DC0,经过FPGA运算后用示波器观察到的波形如图 3(a)所示,将计算结果经过高速采集卡2 MHz采样采集得到的B0信号如图 3(c)所示,其中纵坐标代表各采样点的幅值,根据(9)、(10)式对B0信号从最低点起的衰减部分进行曲线拟合,结果如图 3(e)所示,纵坐标为对应点的幅值,计算所得的确定系数R2 = 0.999 9,起始幅值k= -1.843 0.根据(11)式和(12)式计算得到k理=-1.831 1,误差δk=0.006 5.
|
图 3 (a)大幅度常数的示波器波形;(b)小幅度常数的示波器波形;(c)大幅度常数采集到的波形;(d)小幅度常数采集到的波形;(e)大幅度常数的曲线拟合结果;(f)小幅度常数的曲线拟合结果 Figure 3 (a) Oscilloscope waveform with a large amplitude constant; (b) Oscilloscope waveform with a small amplitude constant; (c) The waveforms collected by the large amplitude constant; (d) The waveforms collected by the small amplitude constant; (e) Curve fitting results of large amplitude constants; (f) Curve fitting results of small amplitude constants |
时间常数不变,将幅度常数减小为原来的1/8,即a= 0xBB8,得到的另外一组示波器波形如图 3(b)所示,经过高速采集卡采集之后的波形如图 3(d)所示,该波形经过曲线拟合的结果如图 3(f)所示,计算所得的确定系数R2 = 0.999 8,起始幅值k= -0.227 6.计算得到k理=-0.228 8,误差δk=0.005 2.
对比两组数据经曲线拟合得到起始幅值与计算所得的理论值的误差,在幅度较大和较小时,其误差都在1%以下,该结果很好的反应了输入幅度常数的线性关系.
3.2 时间常数的参数拟合结果分析时间常数b与理论的衰减率q理的关系如(13)式所示,其中≫”为右移符号,即将b(2进制数)右移13位.衰减率的误差计算公式如(14)式所示.
| $ q_{\rm{理}}^2 = \frac{{(b > > 13)}}{{{2^{18}}}} $ | (13) |
| $ {\delta _q} = \frac{{|q_{\rm{理}}^2 - {q^2}|}}{{q_{\rm{理}}^2}} $ | (14) |
幅度常数固定为0x5DC0,时间常数为b= 0x7FF8FFFF,经过FPGA运算后用示波器观察到的波形如图 4(a)所示,其中纵坐标为幅值,将计算结果经过高速采集卡采集得到的B0信号的结果如图 4(c)所示,对B0信号从最低点起的衰减部分进行曲线拟合,结果如图 4(e)所示,计算所得的确定系数R2 = 1.000 0,衰减率q1=0.999 9,则q12=0.999 8.根据(13)式和(14)式计算得到的q理2=0.999 7,δq=0.000 1.

|
图 4 (a)大时间常数的示波器波形;(b)小时间常数的示波器波形;(c)大时间常数采集到的波形;(d)小时间常数采集到的波形;(e)大时间常数的曲线拟合结果;(f)小时间常数的曲线拟合结果 Figure 4 (a) Oscilloscope waveform with a large time constant; (b) Oscilloscope waveform with a small time constant; (c) The waveform collected by large time constant; (d) The waveform collected by small time constant; (e) Curve fitting results of large time constants; (f) Curve fitting results of small time constants |
将时间常数减小,设为b= 0x7FBCFFFF,示波器观察到的波形如图 4(b)所示,经过采集卡采集到的波形如图 4(d)所示,该曲线经拟合的结果如图 4(f)所示,计算所得的确定系数R2 = 1.000 0,衰减率q2=0.999 0,则q22=0.998 0.计算得到q理2=0.998 0,δq=0.000 0.
对比两组输入的时间常数的比例关系与拟合所得衰减率的关系.(0x7FF8FFFF)/(0x7FBCFFFF) ≈ 0.976 8,q12/q22≈0.976 7.误差为0.000 1.
对比两组数据所得的衰减率与理论值的误差,该结果能够正确反应输入的时间常数的线性关系.
4 结论本文提出了一种基于FPGA的MRI谱仪B0信号的高精度发生方法,此方法利用FPGA的高速运行及丰富的硬件资源,编程具有灵活性.得到的B0信号经数据采集并用Matlab做曲线拟合进行了测试和分析,结果证实此方法可以达到较高的波形分辨率与较高的运算精度.
| [1] |
LIU M, QIU W Q, Sun H J, et al. Progress in the portable NMR spectrometer[J].
Chinese J Magn Reson, 2014, 31(4): 504-514.
刘敏, 邱雯琦, 孙慧军, 等. 便携式核磁共振谱仪的研究进展[J]. 波谱学杂志, 2014, 31(4): 504-514. |
| [2] | SHEN J, LIU Y, LI J Q, et al. A powerful graphical pulse sequence programming tool for magnetic resonance imaging[J]. MAGMA, 2005, 18(6): 332-342. DOI: 10.1007/s10334-005-0021-z. |
| [3] | MAO W P, BAO Q J, YANG L, et al. A modularized pulse programmer for NMR spectroscopy[J]. Meas Sci Technol, 2011, 22(2): 025901. DOI: 10.1088/0957-0233/22/2/025901. |
| [4] | STANG P P, CONOLLY S M, SANTOS J M, et al. Medusa:a scalable MR console using USB[J]. IEEE Trans Med Imaging, 2012, 31(2): 370-379. DOI: 10.1109/TMI.2011.2169681. |
| [5] |
HOU S L, XIE H T, HOU X W, et al. Gradient coil of permanent magnet mini-magnetic resonance imager and image quality[J].
Chinese J Magn Reson, 2014, 29(4): 508-520.
侯淑莲, 谢寰彤, 侯晓吻, 等. 永磁微型磁共振成像仪的梯度线圈与图像质量[J]. 波谱学杂志, 2014, 29(4): 508-520. |
| [6] |
XU Q, WANG H, JIANG Y, et al. A digital preemphasis gradient waveform generator for magnetic resonance imaging[J].
Chinese J Magn Reson, 2006, 23(1): 11-16.
徐勤, 王鹤, 蒋瑜, 等. 一种具有数字预加重的磁共振成像梯度波形发生器[J]. 波谱学杂志, 2006, 23(1): 11-16. |
| [7] |
XIAO L, TANG W N, WANG W M. An FPGA-based single-chip gradient calculation module for magnetic resonance imaging[J].
Chinese J Magn Reson, 2010, 27(2): 163-171.
肖亮, 汤伟男, 王为民. 基于单片FPGA的磁共振成像梯度计算模块[J]. 波谱学杂志, 2010, 27(2): 163-171. |
| [8] |
ZANG F C, LI J Q, WANG H, et al. Automatic adjustment of gradient preemphasis in MRI systems[J].
Chinese J Magn Reson, 2008, 25(1): 26-32.
臧凤超, 李建奇, 王鹤, 等. 磁共振成像系统中的自动梯度预加重调节方法研究[J]. 波谱学杂志, 2008, 25(1): 26-32. |
| [9] |
LIU H D, WANG H W, ZHU T X, et al. A frequency synthesizer for high-field NMR spectrometers[J].
Chinese J Magn Reson, 2014, 31(1): 91-99.
刘海丹, 王辉旺, 朱天雄, 等. 高场核磁共振波谱仪频率合成器设计[J]. 波谱学杂志, 2014, 31(1): 91-99. |
| [10] | FRY M E, PITTARD S, SUMMERS I R, et al. A programmable eddy-current compensation system for MRI and localized spectroscopy[J]. J Magn Reson Imaging, 1997, 7(2): 455-458. DOI: 10.1002/(ISSN)1522-2586. |
| [11] | VARDAL J, SALO R A, LAESSON C, et al. Correction of B0-distortions in echo-planar-imaging-based perfusion-weighted MR[J]. J Magn Reson Imaging, 2014, 39(3): 722-728. DOI: 10.1002/jmri.24213. |
 2018, Vol. 35
2018, Vol. 35 
