2. 中国科学院苏州生物医学工程技术研究所, 江苏 苏州 215163
2. Suzhou Institute of Biomedical Engineering and Technology, Chinese Academy of Sciences, Suzhou 215163, China
核磁共振成像(MRI)是利用外加梯度磁场与射频(RF)脉冲操纵物质内部的原子核(如1H核)核磁矩,从而产生自由感应衰减(FID)信号,据此绘制出物体内部的结构图像.该技术因其组织分辨率高、无电离辐射等显著优势目前已成为临床诊断和安全检测的重要手段[1, 2].常规MRI序列一般采用逐层激发然后进行空间编码操作,其中层选射频脉冲可采用简单的矩形脉冲、Sinc脉冲等.
近年来,为提高成像信号信噪比(SNR)、缩短成像时间,同时多层(simultaneous multi-slice)成像技术受到了极大的关注[3, 4].同时多层成像的关键技术之一就是如何有效实现同时多层的选择性激发.很多磁共振厂商均提供了多层成像序列,如通用电器公司(GE)的phase-offset multi-planar(POMP),西门子公司(Siemens)的simultaneous excitation,飞利浦公司(Philips)的multi-slice等[5-7],这些序列本质上均是由多个独立的幅值相同相位不同的简单脉冲叠加而成.实际应用中,同时多层成像的性能受限于简单脉冲,并且使用的灵活性相对较差.因此,需提出一种新型的同时多层的选择性射频脉冲,能够灵活的实现任意层厚、层间距、层数的选择性激发,并且具有优异的性能,使得同步多层成像技术优势得以充分发挥.
近年来,优化控制理论被引入脉冲设计之中,用于实现形状脉冲的数值优化.德国的Glaser小组[8]首先提出基于梯度信息的GRAPE(gradient ascent pulse engineering)数值优化方法,可在脉冲参数空间的搜索中得到优化脉冲的数值解,从而实现自旋体系状态的最优化转移,该算法鲁棒性好、并能收敛到极值,可适用于任意自旋系统.基于最优控制理论设计的优化脉冲与传统脉冲(如矩形脉冲、Sinc脉冲等)相比,还可以克服带宽激发不均匀、样本弛豫效应等对磁共振信号的影响,因此已应用于MRI领域中,并取得了丰硕的研究成果[9-11].
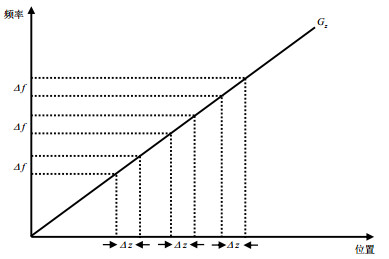
基于自旋动力学和优化控制原理,本文设计了一种针对同时多层的选择性射频脉冲,该射频脉冲在使用时配合层选梯度,可同时实现任意层厚、层间距、层数的高效选择性激发(如图 1所示,脉冲激发层带宽为Δf,配合梯度Gz,可实现层厚为Δz的多层选择性激发).该方法基于GRAPE算法,通过建立合适的形状脉冲的优化控制模型,运用数值迭代方法实现形状脉冲的最优化设计.在实际运用中,利用该脉冲取代成像序列中的常规层选脉冲,可有效提高成像均匀性.该设计方法发挥了优化形状脉冲对自旋体系的灵活精确操控优势,可根据脉冲持续时间、激发层数和激发轮廓等进行优化脉冲的自适应调整,从而有效提高同时多层MRI的性能.
|
图 1 多层层选示意图 Figure 1 Schematic diagram of multi-layer selection |
磁共振脉冲优化是基于自旋磁矩的运动方程和最优控制理论,采用数值方法计算优化脉冲的过程.脉冲优化设计的主要目的在于:保证自旋系统从初始态迁移到目标态的效率值最高,增强激发效果.目前,对磁共振脉冲进行优化设计的方法已经比较成熟,文献[12, 13]分别提出了相应的优化方法.
本文以GRAPE数值迭代算法作为基础,构造针对多宽带脉冲的目标函数,并使优化脉冲在各个频段具有特异性的优化目标,利用梯度信息对目标函数进行相应的数值迭代计算求解,从而得到具有设计激发轮廓的优化脉冲.
1.2 GRAPE算法在磁共振脉冲优化模型中,自旋系统的状态可以使用密度算符ρ(t)来表示,其运动状态则由Liouville–von Neuman方程来描述[14]:
| $ \dot \rho (t) = - {\rm{i}}\left\{ {\left[ {{H_0} + \sum\limits_{k = 1}^m {{u_k}(t){H_k}} } \right], \rho (t)} \right\} $ | (1) |
其中,H0表示是自由演化的哈密顿量,Hk则表示与射频场相关的哈密顿量,uk(t)则表征为控制量.因此,整个数值优化问题的关键就是找到最优的射频脉冲控制量uk(t),使自旋系统由初态有效激发至期望末态.因此,在脉冲作用下由热平衡态迁移到期望态的转移效率即为脉冲优化的目标函数:
| $ \mathit{\Phi} = \left\langle {C\left| {\rho (t)} \right.} \right\rangle $ | (2) |
其中,C为自旋体系的期望末态,ρ(t)为脉冲作用后的实际末态.
为进行数值优化计算,可将形状脉冲离散化至N个离散片段[8],脉冲持续时间为T,则每一个离散化的脉冲片段的时间间隔
| $ {U_j} = \exp \left\{ { - {\rm{i}}\mathit{\Delta} t\left[ {{H_0} + \sum\limits_{k = 1}^m {{u_k}(j){H_k}} } \right]} \right\} $ | (3) |
经过时间长度为T的脉冲作用后,自旋系统的密度算符可以表示为:
| $ \rho (T) = {U_N} \cdot \cdot \cdot {U_1}{\rho _0}U_1^\dagger \cdot \cdot \cdot U_N^\dagger $ | (4) |
此时的目标函数可表示为:
| $ \mathit{\Phi} = \left\langle {C\left| {{U_N} \cdot \cdot \cdot {U_1}{\rho _0}U_1^\dagger \cdot \cdot \cdot U_N^\dagger } \right.} \right\rangle $ | (5) |
此时,目标函数关于脉冲变量的梯度计算如下:
| $ \frac{{\partial \mathit{\Phi} }}{{\partial {u_k}(j)}} = - \left\langle {{\lambda _j}\left| {{\rm{i}}\mathit{\Delta} t\left[ {{H_k}, {\rho _j}} \right]} \right.} \right\rangle $ | (6) |
射频控制量的更新表示为:
| $ {u_k}(j) \to {u_k}(j) + \varepsilon \frac{{\partial \mathit{\Phi} }}{{\partial {u_k}(j)}} $ | (7) |
其中ε为整个优化过程选取的步长,对收敛速度有一定影响,在具体算法中可通过线性搜索得到最优值,使得效率函数得到最大增加.
至此,我们已经在量子体系下将磁共振脉冲优化问题转化为一个最优控制问题.基本GRAPE算法具体步骤总结如下:
1) 初始化脉冲;
2) 从ρ0开始,利用公式
3) 从λj=C开始,利用公式
4) 计算梯度,根据(7)式更新所有控制矩阵;
5) 利用新的脉冲控制矩阵,转至步骤2),重复算法直到目标函数Φ的改变值小于给定阈值时,由此得到的控制矩阵即为优化脉冲.
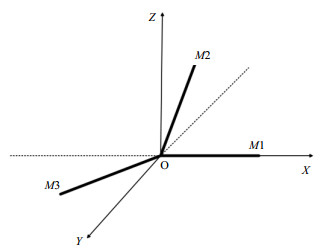
1.3 同时多层射频脉冲设计方法为了使优化脉冲具有多层MRI的选择性,可以利用射频脉冲将激发层的目标磁矩翻转90°,并根据激发层数需求,使不同激发层的目标磁矩具有特异性的自旋相位.图 2为三层脉冲的磁矩分布示意图,激发层的目标磁矩M1、M2、M3均位于与热平衡态垂直的XOY平面中,三层激发层磁矩的自旋相位分别为0°、120°和240°.
|
图 2 磁矩激发分布图 Figure 2 Excitation distribution diagram of magnetic moment |
根据优化脉冲的设计需求(脉冲长度T、多层激发厚度范围、激发层数Ns、层间距、各层厚度、各层目标磁矩状态等)和层选梯度参数,确定脉冲总体激发带宽范围ωa~ωb、各层所属的频带区为
| $ C({w_i}) = \sin \beta \cos {\varphi _i}{I_x} + \sin \beta \sin {\varphi _i}{I_y} + \cos \beta {I_z} $ | (8) |
其中β为所述脉冲的翻转角;φi为层选脉冲施加后的第i层自旋相位,其取值为:
| $ {\varphi _i} = 2{\rm{ \mathsf{ π} }}i/{N_s}, \quad i = 0, \, \;1, \; \cdot \cdot \cdot {N_s} - 1 $ | (9) |
利用目标参数建立最优化控制模型,目标函数F包括激发和层间抑制两个部分:
| $ F = \sum\nolimits_i {\left[ {\int_{\omega _i^a}^{\omega _i^b} \mathit{\Phi} {\rm{(}}{\omega _i}{\rm{)d}}{\omega _i}} \right]} + \sum\nolimits_j {\left[ {\int_{\omega _j^a}^{\omega _j^b} \mathit{\Phi} {\rm{(}}{\omega _j}{\rm{)d}}{\omega _j}} \right]} $ | (10) |
实际数值优化中,可将上述带宽范围离散化为若干频率点,相邻频率点之间的频率间隔满足
| $ F = \sum\nolimits_i {\sum\nolimits_{\omega i} \mathit{\Phi} } ({\omega _i}) + \sum\nolimits_j {\sum\nolimits_{\omega j} \mathit{\Phi} } ({\omega _j}) $ | (11) |
根据上述计算目标函数F的梯度,计算公式为:
| $ \frac{{\partial F}}{{\partial {u_x}(k)}} = \sum\nolimits_i {\sum\nolimits_{\omega i} {\frac{{\partial \mathit{\Phi} ({\omega _i})}}{{\partial {u_x}(k)}}} } + \sum\nolimits_j {\sum\nolimits_{\omega j} {\frac{{\partial \mathit{\Phi} ({\omega _j})}}{{\partial {u_x}(k)}}} } $ | (12) |
其中,ux(k)为同步多层选择脉冲第k段的x分量;同理可获得
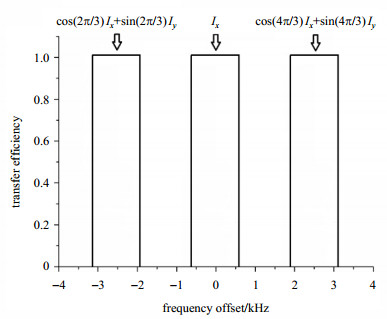
采用上述方法,针对三层层选脉冲进行优化,脉冲持续时间为12 ms,单层及层间厚度均为2 mm,不同层的目标激发轮廓如图 3所示,设定梯度场强度为15 mT/m,则带宽范围为–3.25~3.25 kHz.在优化过程中,将脉冲离散化至1 000个时间片段,单个片段的持续时间为12 μs,取306个带宽控制点,各层及层间的参数如表 1所示.
|
图 3 脉冲设计激发轮廓 Figure 3 Designed pulse excitation profile |
| 表 1 各层参数列表 Table 1 List of parameters |
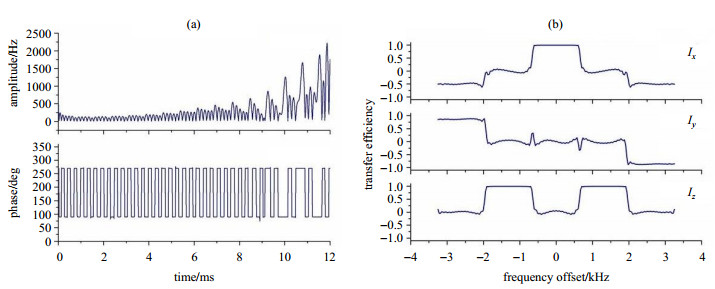
图 4(a)是针对表 1中参数优化得到的脉冲的幅值和相位,脉冲的优化效率为0.991 2,脉冲最大幅值为2 220 Hz.图 4(b)为优化脉冲在各频率点处相对磁矩Ix、Iy、Iz的激发效率,在总带宽范围内取800个频率点计算脉冲的激发效率,从图中可以看出,优化脉冲在各个频率段的与激发效率与预期设计的目标态基本保持一致.
|
图 4 优化脉冲的波形及激发效率.(a)幅值相位;(b)激发效率 Figure 4 Pulse shape and its transfer efficiency. (a) Amplitude and phase; (b) Transfer efficiency |
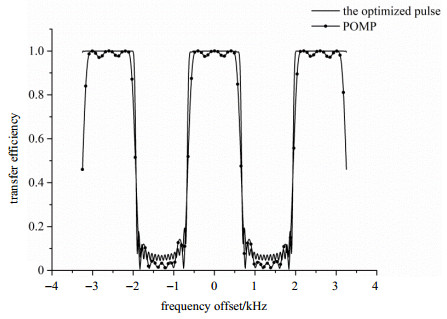
与此同时,通过理论计算获得了优化脉冲总体的激发效率,并将其和使用POMP方法的射频脉冲进行性能比较.其中,POMP射频脉冲为三个幅值相同并存在相位偏移的五瓣Sinc脉冲的叠加,脉冲持续时间为4.6 ms,对应激发带宽为1.3 kHz,激发层选择及带宽参数与表 1一致.图 5为三层层选优化脉冲和POMP脉冲的理论激发效率比较,从图中可以看出,优化脉冲在激发层的边缘具有非常好的激发效率,脉冲激发的平稳性也明显好于POMP方法的脉冲.
|
图 5 脉冲激发效率比较 Figure 5 Transfer efficiency comparison of POMP pulse and the optimized pulse |
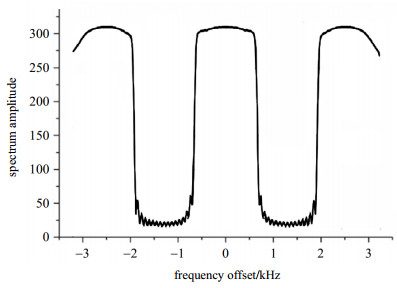
另外,基于自主开发的Spin-Scenario磁共振动力学仿真平台对优化脉冲进行了性能测试,测试脉冲序列为修改的FID序列,即将原始FID序列中的90°射频脉冲替换为优化脉冲,并在–3.25~3.25 kHz的带宽范围内共取400个频率偏移点进行多次仿真实验,采集各个频点产生的FID信号,图 6为仿真实验所获得的FID信号的频谱幅值.由图中可以看出,在三个激发频段,脉冲具有良好的激发效率,使样本达到预期磁矩,产生了一定强度的FID信号,并基本保持稳定;在两个抑制频段,优化脉冲也能使磁矩维持在Iz方向,抑制信号的产生.
|
图 6 仿真实验频谱幅值 Figure 6 Simulated spectrum amplitude |
最后,我们使用上述三层层选脉冲在Spin-Scenario仿真平台中进行了同时多层MRI的仿真实验,并使用MIDA人脑模体[15]作为测试模型(模体大小为480×480×350,分辨率为0.5 mm).三层层选脉冲在成像时会获得三幅属于各自激发层的图像,为了分离各层图像同时不降低信噪比,可将将相位编码方向的成像视野(FOV)也变为原先的3倍,同时相位编码的次数相对应扩大至原先的3倍[4].然而,若简单使用上述优化脉冲进行成像,成像结果仍将重叠在中心位置.为此,需要将激发脉冲加上一个特殊的线性相位[16]:
| $ \mathit{\Phi} \left( m \right) = m\mathit{\Delta} k\mathit{\Delta} y $ | (13) |
其中m代表梯度编码的视图数,Δk为k空间的间距,即
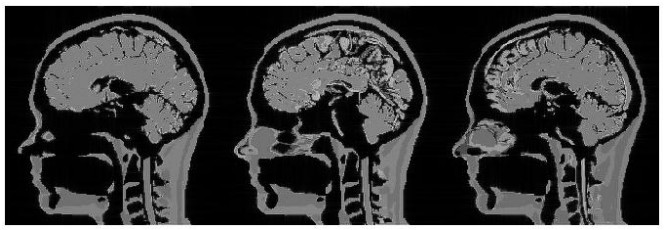
成像实验中采用梯度回波(GRE)作为成像序列,FOV为240 mm×720 mm,成像矩阵大小为256×768,层选梯度大小为15 mT/m.图 7为仿真成像结果,水平为相位编码方向,竖直方向为频率编码方向.可以看出,三层图像依次排布在相位编码方向,实现了同时多层MRI.
|
图 7 MIDA人脑同时三层磁共振图像 Figure 7 The simultaneous 3-slice MR images of MIDA brain |
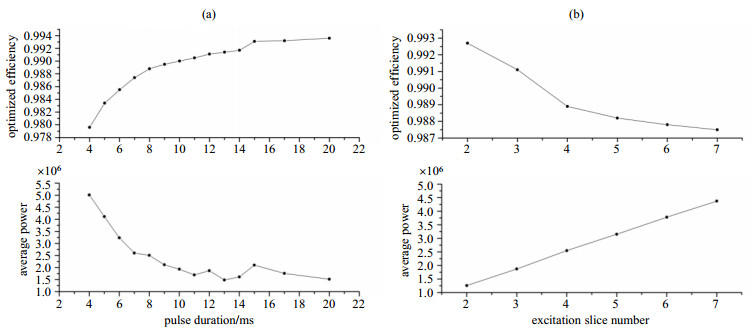
在优化脉冲设计时,为了使其达到最好的性能,我们对各个参数的取值进行了评估,并比较了各参数对脉冲优化的影响.图 8(a)展示的是以三层层选脉冲作为优化目标,脉冲持续时间对脉冲优化效率以及功率的影响.从图中可以看出,随着脉冲优化时间的增加,脉冲的优化效率最初能够显著的上升,但是由于带宽控制点的同时增加,渐渐趋于稳定.脉冲的平均功率最初也随着时间增加而大幅减小,最终也趋于稳定.
|
图 8 (a) 不同脉冲时间及(b)不同激发层数的脉冲性能比较 Figure 8 Performance comparison of different pulse duration (a) and excitation slice number (b) |
另外,脉冲的激发层数也影响脉冲优化效率以及功率,以持续时间为10 ms的多层激发优化脉冲为例,如图 8(b)所示,随着激发层数的增加,脉冲的优化效率逐渐减小,功率也随之显著上升.因此,在多层射频脉冲的设计时,选取合适的激发层数及持续时间显得尤为重要.
3 结论本文提出了一种针对同时多层射频脉冲的优化设计方法,利用获得的优化脉冲,配合层选梯度,可同时实现任意层厚、层间距、层数的高效选择性激发.文中以三层层选脉冲为例对其进行了优化设计,并对其激发效果的进行了仿真验证,同时也完成了三层层选脉冲的仿真成像测试.仿真结果表明,采用本文方法获得的优化脉冲在各层选频段有着良好的激发效果,在层间频段也有着不错的抑制效果,并且能获得清晰的成像结果.因此,该方式设计的优化脉冲在应用于MRI能够有效提高信号信噪比和成像的性能.但是,该方法设计的优化脉冲也存在功率相对偏大的问题,为了应对这一问题,在磁共振序列设计时可以采用VR(variable-rate)脉冲[17]来减小射频脉冲的功率.最后,文中比较了不同的激发层数以及脉冲时间对优化脉冲的效率及功率的影响,为优化脉冲的参数选择提供了一定的参考依据.
| [1] | 赵喜平. 磁共振成像系统的原理及其应用[M]. 北京: 科学出版社, 2000. |
| [2] |
WANG X H, SUN P, ZHANG X, et al. Application of magnetic resonance technique to quality and safety evaluation of food[J].
Chinese J Magn Reson, 2017, 34(2): 245-256.
王小花, 孙鹏, 张许, 等. 磁共振技术在食品质量与安全研究中的应用[J]. 波谱学杂志, 2017, 34(2): 245-256. |
| [3] | MOELLER S, YACOUB E, OLMAN C A, et al. Multiband Multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain FMRI[J]. Magn Reson Med, 2010, 63(5): 1144-1153. DOI: 10.1002/mrm.22361. |
| [4] | SOUZA S P, SZUMOWSKI J, DUMOULIN C L, et al. SIMA:simultaneous multislice acquisition of MR images by Hadamard-encoded excitation[J]. J Comput Assist Tomo, 1988, 12(6): 1026-1030. DOI: 10.1097/00004728-198811000-00021. |
| [5] | GLOVER G H. Phase-offset multiplanar (POMP) volume imaging:a new technique[J]. J Magn Reson Imaging, 1991, 1(4): 457-461. DOI: 10.1002/(ISSN)1522-2586. |
| [6] | LARKMAN D J, HAJNAL J V, HERLIHY A H, et al. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited[J]. J Magn Reson Imaging, 2001, 13(2): 313-317. DOI: 10.1002/(ISSN)1522-2586. |
| [7] | LEE K J, WILD J M, GRIFFITHS P D, et al. Simultaneous multislice imaging with slice-multiplexed RF pulses[J]. Magn Reson Med, 2005, 54(4): 755-760. DOI: 10.1002/(ISSN)1522-2594. |
| [8] | KHANEJA N, REISS T, KEHLET C, et al. Optimal control of coupled spin dynamics:design of NMR pulse sequences by gradient asce nt algorithms[J]. J Magn Reson, 2005, 172(2): 296-305. DOI: 10.1016/j.jmr.2004.11.004. |
| [9] | SKINNER T E, GERSHENZON N I. Optimal control design of pulse shapes as analytic functions[J]. J Magn Reson, 2010, 204(2): 248-255. DOI: 10.1016/j.jmr.2010.03.002. |
| [10] | MASSIRE A, CLOOS M A, VIGNAUD A, et al. Design of non-selective refocusing pulses with phase-free rotation axis by gradient ascent pulse engineering algorithm in parallel transmission at 7 T[J]. J Magn Reson, 2013, 230: 76-83. DOI: 10.1016/j.jmr.2013.01.005. |
| [11] |
ZHANG S L, CHANG Y, YANG X D. Optimization of limited amplitude radiofrequency pulse with variance evaluation[J].
Chinese J Magn Reson, 2015, 32(3): 462-469.
张树林, 常严, 杨晓冬. 方差评估在幅值限制脉冲优化中的应用[J]. 波谱学杂志, 2015, 32(3): 462-469. |
| [12] | VINDING M S, MAXIMOV I I, TOSNER Z, et al. Fast numerical design of spatial-selective rf pulses in MRI using Krotov and quasi-Newton based optimal control methods[J]. J Chem Phys, 2012, 137(5): 054203. DOI: 10.1063/1.4739755. |
| [13] | KHANEJA N, BROCKETT R, GLASER S. Time optimal control in spin systems[J]. Phys Rev A, 2000, 63(3): 222-224. |
| [14] | ERNST R R, BODENHAUSEN G, WOKAUN A, et al. Principles of nuclear magnetic resonance in one and two dimensions[M]. Oxford: Clarendon Press, 1987. |
| [15] | IACONO M I, NEUFELD E, AKINNAGBE E, et al. MIDA:A multimodal imaging-based detailed anatomical model of the human head and neck[J]. Plos One, 2015, 10(4): e0124126. DOI: 10.1371/journal.pone.0124126. |
| [16] | STAB D, RITTER C O, BREUER F A, et al. CAIPIRINHA accelerated SSFP imaging[J]. Magn Reson Med, 2011, 65(1): 157-64. DOI: 10.1002/mrm.22600. |
| [17] | STOYAN J S. Variable rate selective excitation RF pulse in MRI[D]. Hamilton: McMaster University, 2004. https://macsphere.mcmaster.ca/handle/11375/13077 |
 2018, Vol. 35
2018, Vol. 35 
