引言

铷原子频标由于具有体积小、重量轻、功耗低等优点，是目前应用最多的原子频标.早期的铷频标性能指标不高，但近年来在卫星导航等重要应用需求牵引下，铷频标频率稳定度得到长足的提升.例如，美国GPS系统所用最新型号卫星星载铷频标，短期稳定度优于$ 1\times {{10}^{-12}}{{\tau }^{-1/2}} $，天稳约为5×10^-15[1]，接近被动氢原子频标的水平.这在二十年前是不可想象想的，从而引发了人们探索铷频标稳定度极限的兴趣.

铷频标的频率稳定度与铷原子钟跃迁信号的信噪比相关.原子信号是由微波场与铷吸收泡中的铷蒸气原子相互作用产生的，故信号强度与微波腔的特性直接相关.近年来，本实验室利用自主研发的开槽管式微波腔^[2]，通过改进微波场与量子化轴的平行度和适当增大微波腔直径（以便采用直径更大的铷吸收泡），在提高铷原子信号信噪比和改善铷频标频率稳定度方面取得了系统性的进展.实验室早期研制的铷原子频标，采用了内径为14 mm的微波腔，频率稳定度在$ 2.5\times {{10}^{-12}}{{\tau }^{-1/2}} $^{[2, 3]}水平.随后，许风等^[4]将微波腔内径增大至20 mm，铷频标稳定度改善到约$ 5\times {{10}^{-13}}{{\tau }^{-1/2}} $水平.Hao等^[5]利用场平行度高达0.93、直径为30 mm的开槽管腔设计的铷频标桌面系统，稳定度达到$ 2.4\times {{10}^{-13}}{{\tau }^{-1/2}} $，这是目前世界上最好的结果.

本文的目的是设计一款内径为40 mm的开槽管微波腔，用于铷频标物理系统，探索进一步提高铷频标频率稳定度的可能性.

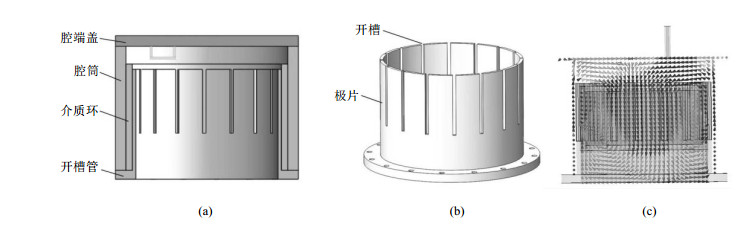
1 微波腔设计

我们设计的微波腔主要由圆柱腔筒、开槽管和介质环构成，示于图 1(a).开槽管是腔的核心，如图 1(b)所示，其上端开有若干个槽，通过调整开槽管内径、槽宽、槽深、槽的数目以及介质环长度等参数，可以调整腔的谐振频率和微波场模式^[6].开槽管的内径为40 mm，以便容纳外径为40 mm的铷吸收泡.其他结构参数的优化通过HFSS软件建模仿真实现.最终得到的腔谐振频率为铷原子钟跃迁频率6 834.5 MHz，微波场的分布示于图 1(c).由图 1(c)可以初步看出，在电极和槽所围成的区域，即铷吸收泡所在的微波场与原子作用区，磁力线与腔轴基本平行.由于铷频标的钟跃迁是磁偶极跃迁，只有平行于量子化轴（一般为腔轴）的磁场分量才能激励这种跃迁，所以图 1(c)所示的场分布对获取高强度原子跃迁信号是有利的.

微波场磁力线与腔轴的平行度用方向因子（ξ）描述，它定义为平行于腔轴方向的磁场分量的强度与微波总强度之比^[7]：

$ \xi =\frac{\int_{V}{{{H}_{z}}^{2}\text{d}V}}{\int_{V}{{{\left| H \right|}^{2}}\text{d}V}} $

(1)

方向因子可以利用HFSS软件直接计算.其中$ \int_{V}{{{H}_{z}}^{2}\text{d}V} $和$ \int_{V}{{{\left| H \right|}^{2}}\text{d}V} $是平行于腔轴方向的磁场分量的强度和微波总强度，图 1(a)所示微波腔方向因子的计算结果为0.87，远高于一般常用的微波腔.

2 物理系统设计和微波场方向因子测量

利用上述开槽管微波腔，设计了一个铷频标物理系统，以便对微波腔的特性进行检验.物理系统主要由铷光谱灯、干涉滤光片、同位素滤光器和腔泡系统组成.光谱灯发出的光，经由透镜准直后，经过干涉滤光片滤除杂散光，然后进入充有⁸⁵Rb金属的滤光泡进行同位素滤光，最后对吸收泡内的⁸⁷Rb原子蒸气进行光抽运，使两个钟跃迁能级的布居数产生反转.将微波信号馈入微波腔，激励吸收泡中的⁸⁷Rb原子发生钟跃迁，导致光电池检测的光信号发生改变.光检信号经过处理后，转变为误差信号，对微波信号进行纠偏，从而实现一个完整的铷频标系统.

微波腔中微波场的方向因子可以利用物理系统进行实验测量.将频率为6 834.35 MHz的微波通入物理系统，扫描微波频率，可以得到⁸⁷Rb原子基态各能级间塞曼跃迁谱线，再根据谱线强度进行计算，即可得到方向因子的实验测量值^[4].设S_σ、$ {{S}_{{{\pi }_{-}}}} $和$ {{S}_{{{\pi }_{+}}}} $分别代表（|F=2, m_F=0＞→|F=1, m_F=0＞）跃迁、（|F=2, m_F=0＞→|F=1, m_F=-1＞, |F=2, m_F=+1＞→|F=1, m_F=0＞）跃迁和（|F=2, m_F=0＞→|F=1, m_F=+1＞, |F=2, m_F=-1＞→|F=1, m_F=0＞）跃迁谱线的跃迁几率，积分后得到相应跃迁谱线的信号强度，则微波场方向因子可由下式计算：

$ \xi =\frac{\int{{{S}_{\sigma }}\text{d}v}}{\int{{{S}_{{{\pi }_{-}}}}\text{d}v}+\int{{{S}_{{{\pi }_{+}}}}\text{d}v}+\int{{{S}_{\sigma }}\text{d}v}} $

(2)

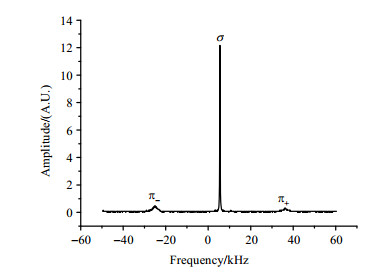
测量得到的⁸⁷Rb的基态塞曼跃迁谱示于图 3.利用(2)式，可以得到微波腔方向因子的测量值为0.91，与仿真计算得到的结果基本一致.这表明该微波腔的微波场模式优越，可用于高性能铷频标设计.

3 铷频标频率稳定度评估

频率稳定度是铷频标的核心指标.铷频标频率稳定度主要取决于物理系统原子跃迁信号的信号强度和噪声水平.原子信号噪声主要是由光电池在光电测量过程中引入的散弹噪声.散弹噪声功率谱密度$ {{S}_{I}}(f) $的表达式为^[8]：

$ {{S}_{I}}(f)=2e{{I}_{0}} $

(3)

其中e为电子电荷量，I₀为背景光电流.物理系统原子信号功率谱密度$ {{S}_{y}}(f) $可表示为^[8]：

$ {{S}_{y}}(f)=2\frac{{{S}_{I}}(f)}{K_{D}^{2}v_{0}^{2}}=\frac{4e{{I}_{0}}}{K_{D}^{2}v_{0}^{2}} $

(4)

其中$ {{v}_{0}} $为钟跃迁频率，K_D是鉴频斜率.由于散弹噪声为白频噪声，故由物理系统决定的铷频标的频率稳定度$ {{\sigma }_{y}}(\tau ) $可以用Allan方差表示为：

$ {{\sigma }_{y}}(\tau )=\sqrt{\frac{{{S}_{y}}(f)}{2}}{{\tau }^{-1/2}} $

(5)

将(4)式代入(5)式可得：

$ {{\sigma }_{y}}\left( \tau \right)=\frac{\sqrt{2e{{I}_{0}}}}{{{v}_{0}}{{K}_{D}}}{{\tau }^{-1/2}} $

(6)

由(6)式可以看出，频率稳定度由鉴频斜率和背景光电流共同决定.

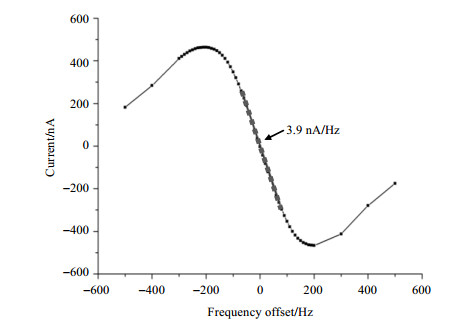
我们实测了基于内径40 mm开槽管微波腔得到的物理系统（图 2）的鉴频斜率和背景光电流.实验得到的鉴频曲线示于图 4.在中心频率±100 Hz范围内，鉴频曲线的斜率即鉴频斜率为3.9 nA/Hz.背景光电流的测量值为70 µA.将试验得到的鉴频斜率和背景光电流代入(6)式，计算得到由物理系统决定的频率稳定度为$ 1.8\times {{10}^{-13}}{{\tau }^{-1/2}} $.该结果已经优于文献^[5]报道的目前世界最优的稳定度.

对于一个实际的铷频标，频率稳定度还依赖于电子学系统的噪声水平.Francois等^[9]最近研制出一款用于铷频标的低噪声电子学系统，系统相位噪声对稳定度的影响为$ 2\times {{10}^{-14}}{{\tau }^{-1/2}} $，所以电子学系统不是限制铷频标频率稳定度的主要因素.因此我们相信，铷原子频标的频率稳定度达到优于$ 2\times {{10}^{-13}}{{\tau }^{-1/2}} $的水平是可以实现的.

4 结论

为了探索铷原子频标稳定度的极限，我们设计了一款内径为40 mm的大尺寸开槽管微波腔.微波腔内微波场方向高度平行于腔轴，方向因子的理论仿真结果和实验测量结果分别为0.87和0.91，基本一致.利用该微波腔，设计一款铷原子频标物理系统.测量了物理系统的鉴频斜率和背景光电流，根据测量结果预期了铷频标的频率稳定度，结果为$ 1.8\times {{10}^{-13}}{{\tau }^{-1/2}} $.这表明适当增大开槽管微波腔的尺寸，可以进一步改善铷原子跃迁信号的信噪比，同时还表明铷原子频标的频率稳定度可以达到优于$ 2\times {{10}^{-13}}{{\tau }^{-1/2}} $的水平.