2. 上海纽迈电子科技有限公司, 上海 200333;
3. 双钱集团上海轮胎研究所有限公司, 上海 200237;
4. 同济大学 材料科学与工程学院, 上海 201804
2. Shanghai Niumag Electronic Technology Co., Ltd., Shanghai 200333, China;
3. Double Coin Group Shanghai Tire Research Institute Co., Ltd., Shanghai 200237, China;
4. School of Materials Science and Engineering, Tongji University, Shanghai 201804, China
交联密度是表征交联聚合物中交联键数量的物理量,一般用交联点之间的相对分子质量(Mc)表示[1].交联密度对橡胶的力学性能有很大的影响:交联密度越大,硬度、定伸强度越小[2].有多种技术可以用来观测橡胶的交联密度:化学法是利用某些交联剂与反应生成的交联键成定量关系的特点来计算交联密度,但对于反应较为复杂的体系,定量关系难以准确获得[3];力学测试法[4]的原理是橡胶弹性模型和交联密度的关系很大程度上依赖于网络变形模型,但是对高交联密度的测量会产生较大误差[1];平衡溶胀法是利用交联聚合物溶胀前后体积的变化来计算交联密度,但是测试周期长[5].
核磁共振(NMR)技术是一种测量硫化胶交联密度的有效手段[6].Gennes[7]于1971年率先报道了基于NMR的橡胶交联密度测量方法.Kuhn[8, 9]在Gennes的基础理论和实验结果的基础上对硫化胶的网络结构和交联密度进行了详细的研究,结果证明NMR中横向弛豫参数和传统的表征硫化胶交联密度的方法之间有良好的相关性.Fedotov和Schneider[10]对此进行了进一步的研究,建立了NMR弛豫参数和交联密度之间的关系.目前,在众多基于NMR的橡胶交联密度测量方法中,1H DQ NMR[11-13]以及基于Hahn回波[14]的“CPMG”(Carr-Purcell-Meiboom-Gill)回波法[15, 16]应用最为广泛.Baum和Pines[17]于1986年开发了1H DQ脉冲序列,该序列可以通过测量双量子相干效率获得所测体系中残余偶极相互作用(Dres).Kay等[18-21]建立了Dres与Mc之间的关系.1990年,Kuhn等[8, 9]提出,通过CPMG实验测得的质子横向弛豫可以获得橡胶的交联密度,Heuert等[22-24]利用CPMG实验对大量橡胶样品进行了测试.不过,由于在高分子体系中CPMG实验测得的质子横向弛豫曲线对90°脉冲和180°脉冲间的间隔时间存在依赖性[25],普通的CPMG实验并不是一种测量橡胶交联密度的合适方法.在之前的工作中,我们针对CPMG实验的这一缺点进行了初步探讨,提出了可以通过对不同脉冲间隔时间下CPMG实验获得的质子横向弛豫曲线进行叠加的方式来改善上述CPMG实验的缺点.
在本文工作中,我们对不同脉冲间隔时间下CPMG实验测得的质子横向驰豫曲线进行高斯加权求和,以实现对橡胶Mc的精确测量.我们的方案可获得与1H DQ NMR方法相同、或更佳的天然橡胶交联密度-材料硬度相关性.同时,我们的方案比1H DQ NMR方法更为高效,整体测量时间缩短为1H DQ NMR实验时间的1/10.
1 实验部分 1.1 仪器与试剂仪器:Bruker AVANCE Ⅲ 300型NMR谱仪(Bruker)、VTMR20-010V-T型交联密度测试仪(上海纽迈电子科技有限公司)、XK-250型开炼机(上海橡胶机械一厂)、XLB-D型平板硫化机(湖州顺力橡胶机械公司)、H10KL型拉力机(Tinius Olsen)、HTS-200A数显邵氏硬度计(上海精密仪器仪表有限公司).
药品与试剂:泰国20#标准胶(上海双钱橡胶有限公司)、硬脂酸(江苏昆宝集团有限公司)、氧化锌(京华氧化锌有限公司)、炭黑(上海卡博特有限公司)、硫磺(江苏宏泰橡胶助剂有限公司).
1.2 实验过程 1.2.1 试样准备本文所用的天然橡胶为泰国标准胶.先将天然橡胶在XK-250型开炼机上塑炼,待胶料表面光滑后,依次加入硬脂酸、氧化锌、炭黑和其他配合剂,最后加入硫磺,打三角包,薄通后出片,硫磺的份数为4 phr(每100 g橡胶中加入4 g的硫磺).停放4 h后,用XLB-D型平板硫化机进行硫化,硫化温度为150 ℃,分别在硫化7 min、10 min、13 min、20 min、30 min以及60 min时取出部分胶料以备后续测试.
1.2.2 CPMG实验测量橡胶交联密度对于硫化橡胶来说,交联分为化学交联和物理交联,化学交联是链与链之间通过化学键连接,如硫化胶中的碳-硫键,物理交联则是由链缠结所产生的交联点.图 1为高分子网络模型示意图[22, 23, 26], 弹性高分子包含三种不同的链段形式,分别是(a)两端受到交联点束缚的交联链,它的链段运动性很差;(b)一端受到交联点束缚的悬垂链,它的链段运动性好于交联链;(c)体系中未受到束缚的自由链,它的链段运动性最好.

|
图 1 高分子网络模型.模型中展示了三种不同的结构成分:(a)交联链、(b)悬垂链和(c)自由链(溶剂化链段) Figure 1 The model of polymer network. Three different structural components, i.e. the inter-crosslinked chain (a), dangling chain (b) and free chain (sol part) (c), are illustrated in this model |
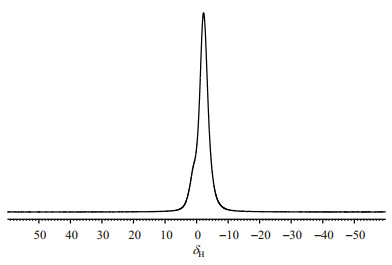
图 2以硫化7 min橡胶的静态1H NMR谱为例,展示了橡胶样品的静态谱线特征.该谱图在Bruker AVANCE Ⅲ 300型NMR谱仪上利用90°单脉冲实验获得.实验条件:90°脉宽为4 μs,CPMG序列中脉冲间隔时间(τ)根据实验目的设定,取值在0.05~0.65 ms之间,实验循环等待时间为2 s,累加次数为4,实验温度为90 ℃.图 2静态1H NMR谱的信号是由一个较强的主峰与主峰左侧的一个较弱信号组成.这些信号来源于橡胶分子的CH3、-CH2-和
|
图 2 典型的橡胶静态1H NMR谱.样品为硫化7 min的天然橡胶.NMR实验温度为90 ℃ Figure 2 A typical static 1H NMR spectrum of rubber. The sample was a natural rubber having a curing time of 7 min, and the temperature of this NMR experiment was 90 ℃ |
通常,橡胶在玻璃化转变温度(Tg)以上时[23],质子横向弛豫可以通过基于单条分子链模型和管状模型的理论方程(1)式来表示:
| $ \frac{{{M_t}}}{{{M_0}}} = A\exp ( - t/{T_2} - 0.5q{M_2}{t^2}) + B\exp ( - t/{T_2}) + C\exp ( - t/{T_{2s}}) + {A_0} $ | (1) |
(1) 式中,
溶胶信号来源于橡胶材料中的小分子。通常来说,溶胶分子含量较少,为了简化拟合的过程,可以假设溶胶信号为0,简化后为(2)式:
| $ \frac{{{M_t}}}{{{M_0}}} = A\exp ( - t/{T_2} - 0.5q{M_2}{t^2}) + B\exp ( - t/{T_2}) + {A_0} $ | (2) |
Gotlib等[27]提出在Tg之上的二阶矩的比率因子q,可用于计算橡胶交联点间的平均分子量Mc.Mc的计算公式见(3)式:
| $ {M_{\rm{c}}} = \frac{{3c{M_{ru}}}}{{5n\sqrt q }} $ | (3) |
(3) 式中c = 7.2,为Kuhn链段内的主链键数;Mru是重复单元内的摩尔质量,单位为g/mol,n为重复单元内的主链键数.天然橡胶的单体为异戊二烯,所以Mru/n = 68/4(g/mol).
本文在VTMR20-010V-T型低场NMR交联密度测试仪上采用CPMG实验测量橡胶的质子横向弛豫,该谱仪磁场强度为0.517 T,90°和180°脉宽分别为2.8 μs和5.8 μs,等待时间为2 s,累加次数为8,单次CPMG实验时间为16 s.我们对CPMG实验中使用的脉冲间隔时间进行了调整,13个不同脉冲间隔时间的CPMG实验总耗时约3.5 min.实验温度为90 ℃.该实验温度的选择是基于文献中已有的报道:测量天然橡胶交联密度的实验温度需高于天然橡胶的Tg 120 ℃[28].
1.2.3 1H DQ NMR测量橡胶交联密度Baum和Pines[17]于1986年发表了1H DQ NMR实验的脉冲序列,整个脉冲序列由激发组合脉冲和恢复组合脉冲两部分组成,这两部分组合脉冲是相同的,只是相位有所不同.第一部分的激发组合脉冲能激发天然橡胶体系内所有的偶量子数相干,而第二部分的恢复组合脉冲则将所有高阶相干恢复到可观测状态.之后通过相位循环得到两组数据,分别是双量子信号和参考信号,用IDQ和Iref来表示.IDQ包括受偶极相互作用影响的信号和所有(4n+2)阶相干的信号,而Iref则是由未偶合组分(各向同性运动部分)和4n阶相干信号组成.因此(IDQ+Iref)就包含了受弛豫作用影响的所有信号,但是必须要减去信号中由运动性较好的末端链所带来的影响,文献[18]详细地说明了1H DQ NMR实验的数据处理过程.归一化的DQ累积信号可用(4)式表示:
| $ {I_{n{\rm{DQ}}}} = \frac{{{I_{{\rm{DQ}}}}}}{{{I_{{\rm{DQ}}}} + {I_{{\rm{ref}}}} - f\exp ( - 2{\tau _{{\rm{DQ}}}}/{T_{{\rm{2, tail}}}})}} $ | (4) |
其中
根据静态二阶矩近似理论,当InDQ≤0.45时,归一化的DQ累积曲线可用(5)式进行描述[18-20]:
| $ {I_{n{\rm{DQ}}}}({D_{{\rm{res}}}}) = \frac{1}{2}\left[{1-\exp (-\frac{2}{5}D_{{\rm{res}}}^2\tau _{{\rm{DQ}}}^2)} \right] $ | (5) |
其中Dres是表观偶极相互作用参数,代表许多不同自旋的偶极相互作用的平均值,与交联点间的分子量Mc成反比,对天然橡胶来说,Dres和Mc的关系如(6)式[18-21]所示:
| $ {M_{\rm{c}}}({\rm{NR}}) = \frac{{617\, {\kern 1pt} {\rm{Hz}}}}{{{D_{{\rm{res}}}}/2{\rm{ \mathsf{ π} }}}}\ {\rm{ kg/mol}} $ | (6) |
在本文的工作中,1H DQ NMR实验使用Bruker AVANCE Ⅲ 300型NMR谱仪,实验温度为90 ℃, 磁体场强为7.04 T,使用4 mm静态探头,90°和180°脉宽分别为4 μs和8 μs,等待时间为2 s,累加次数为8,双量子相干通过组合脉冲90°-τ-90°激发,脉冲间隔时间τ为400 μs.在上述实验条件下,单个1H DQ NMR实验耗时约34 min.
1.2.4 橡胶硬度的测试交联密度对橡胶的弹性、拉伸强度、硬度等力学性能有很大的影响,其中硬度是指材料局部抵抗硬物压入其表面的能力,对于硬度较小的橡胶材料硬度的测量常使用A型邵氏硬度计.刘天琦等[29]发现硬度随着Mc的变大而变小,并且两者近似为负线性相关.
硬度利用HTS-200A数显邵氏硬度计测试,以下为本文中测试橡胶硬度的标准流程:将硬度计的钢制压针在试验力作用下压入试样表面,当压足平面与试样表面紧密贴合时,测量压针相对压足平面的伸出长度.邵氏硬度是以伸出长度来表示,以0.025 mm的伸出长度为邵氏单位HA.邵氏硬度(HA)与伸出长度l的关系见(7)式:
| $ HA = 100 - \frac{l}{{0.025}} $ | (7) |
相关性分析是用来揭示变量之间是否存在相关性及相关密切程度的一种统计学方法,相关性系数r越接近1,说明两组数据的正相关性越好,r越接近-1,说明两组数据的负相关性越好.我们使用Excel中的Correl函数计算不同方法测试结果之间的相关性系数r,相关性系数的计算见(8)式.
| $ r = {\rm{Correl}}(X, Y) = \frac{{\Sigma (x - \bar x)(y - \bar y)}}{{\sqrt {\Sigma {{(x - \bar x)}^2}\Sigma {{(y - \bar y)}^2}} }} $ | (8) |
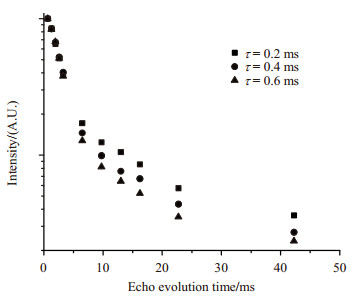
CPMG实验是经常用来测量横向弛豫的一种脉冲序列.从脉冲序列的构成上来看,CPMG实验就是由一系列的Hahn回波组成,更适合在主磁场均匀性较差的低场NMR谱仪测量质子横向弛豫.这是因为和Hahn回波序列相比,CPMG实验对磁场的不均匀性具有更好的汇聚消除作用.在本文的工作中,我们利用CPMG实验对硫化时间为7 min、10 min、13 min、20 min、30 min和60 min的橡胶进行了质子横向弛豫的测量,每个样品的实验时间为16 s.图 3中以硫化7 min的橡胶为例展示了不同脉冲间隔时间下CPMG实验测得的质子横向弛豫,方形、圆形和三角形图标分别表示CPMG序列中脉冲间隔时间τ为0.2 ms、0.4 ms和0.6 ms时测得的质子横向弛豫.分析图 3,我们发现1H核的信号强度随着CPMG序列中脉冲间隔时间的增加而逐渐变小,该现象为质子的横向弛豫过程.将质子横向弛豫曲线利用(2)式拟合可以得到二阶矩的比例因子q,将q代入(3)式可计算交联点间的相对分子质量Mc.当CPMG序列中脉冲间隔时间不同时,我们发现CPMG实验测得的质子横向弛豫速率不同,CPMG序列中脉冲间隔时间越大,质子横向弛豫衰减的越快.该现象与Bremner等[30]的报道一致,他们解释了导致该现象的原因:材料内部存在的空隙会引起局部磁场的不均匀,在空隙周围的高分子链段便是在不均匀磁场下进行运动.尽管在高分子链段运动的时间尺度上,该不均匀场是恒定的,但由于高分子材料中链段运动具有宽分布特征,特定脉冲间隔时间的CPMG序列对不同运动频率的链段信号具有不同的重聚作用,这导致1H CPMG序列测得的质子横向弛豫依赖于实验中所使用的脉冲间隔时间.
|
图 3 CPMG实验测得的硫化7 min的天然橡胶样品的质子横向驰豫曲线.CPMG序列中脉冲间隔时间(τ)分别为0.2 ms、0.4 ms和0.6 ms,实验温度为90 ℃ Figure 3 1H transverse relaxation curves of a natural rubber sample having a curing time of 7 min using CPMG sequence. The interval times between the pulses (τ) in the CPMG experiments were 0.2 ms, 0.4 ms and 0.6 ms, respectively. And the temperature of the NMR experiments was 90 ℃ |
为了深入地研究CPMG序列中脉冲间隔时间τ对橡胶交联密度NMR测量值的影响,我们对脉冲间隔时间进行了细化设计.我们将该时间的范围定为0.05~0.65 ms,以0.05 ms为间隔,共以13种脉冲间隔时间对6个不同硫化时间的橡胶样品进行了CPMG测量.表 1列出了上述总共78个实验所获得的交联点间的相对分子质量Mc.
| 表 1 通过CPMG实验测量橡胶样品所得的Mc值.脉冲间隔时间(τ)为:0.05 ms、0.10 ms、0.15 ms、0.20 ms、0.25 ms、0.30 ms、0.35 ms、0.40 ms、0.45 ms、0.50 ms、0.55 ms、0.60 ms和0.65 ms.橡胶样品为具有不同硫化时间的同种橡胶,硫化时间为:7 min、10 min、13 min、20 min、30 min和60 min Table 1 The acquired Mc values of rubber sample, using CPMG pulse sequence with the different interval times. The interval times between the pulses in the CPMG pulse sequence were 0.05 ms, 0.10 ms, 0.15 ms, 0.20 ms, 0.25 ms, 0.30 ms, 0.35 ms, 0.40 ms, 0.45 ms, 0.50 ms, 0.55 ms, 0.60 ms and 0.65 ms, respectively. The curing times of rubber sample are 7 min, 10 min, 13 min, 20 min, 30 min and 60 min, respectively |
分析表 1中的数据,我们发现同一脉冲间隔时间下,Mc随着硫化时间一般先变小后变大.当硫化时间较小时,此时处在硫化反应初期,交联点不断形成,交联密度逐渐变大.当交联剂硫磺消耗完毕后,硫化反应停止,此时发生过硫反应,部分交联键出现断裂.
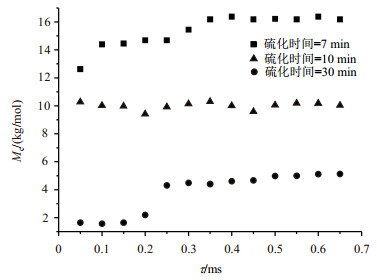
比较表 1中的数据,我们还发现脉冲间隔时间不同时,CPMG实验测得的同一硫化时间的橡胶样品的Mc存在明显的差异.为此我们以硫化7 min、10 min和30 min的橡胶为例,绘制了交联点间的相对分子质量Mc随CPMG序列中脉冲间隔时间的变化(图 4),结果显示Mc对CPMG序列中脉冲间隔时间存在很大的依赖性.这是因为脉冲间隔时间不同时,CPMG实验测得的质子横向驰豫不同,所以得到的Mc也不同.由于使用不同脉冲间隔时间的CPMG实验对质子信号具有不同的汇聚效果,因此使用特定脉冲间隔时间可能意味着对材料中不同运动性的高分子链段质子信号进行了“选择性”观测.
|
图 4 不同脉冲间隔时间(τ)下CPMG实验测得的Mc.样品的硫化时间分别为7 min、10 min和30 min Figure 4 Mc measured by CPMG sequence at different interval times between pulses (τ). The curing times of the samples were 7 min, 10 min and 30 min, respectively |
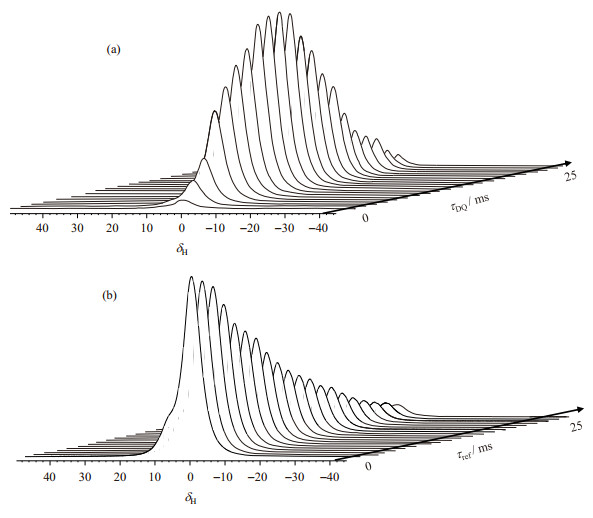
1H DQ NMR实验样品与上述CPMG所用样品相同.在图 5中,我们以硫化时间为7 min的胶料为例展示了1H DQ NMR实验的数据处理过程.图 5(a)为不同双量子激发时间下橡胶的质子信号,双量子激发时间τDQ为0.4~25.0 ms.质子信号强度先上升后下降,信号上升是因为受到了双量子的激发,信号下降是因为产生的驰豫作用.图 5(b)为不同单量子激发时间下橡胶的质子信号,单量子激发时间τref为0.4~25.0 ms,质子信号逐渐减弱.
|
图 5 1H DQ NMR实验谱图. (a)不同双量子激发时间下双量子信号的堆积谱;(b)不同单量子激发时间下参考信号的堆积谱.方便起见,我们将谱图中主峰信号的化学位移定为δH 0.样品为硫化7 min的天然橡胶样品.实验温度为90 ℃ Figure 5 1H DQ NMR spectra: (a) The stacked DQ spectra at different excitation times; (b) The stacked reference spectra at different excitation times. For a convenient reason, the chemical shift of the main peak in the spectra was set to δH 0. The sample was a natural rubber having a curing time of 7 min, and the temperature of the NMR experiments was 90 ℃ |
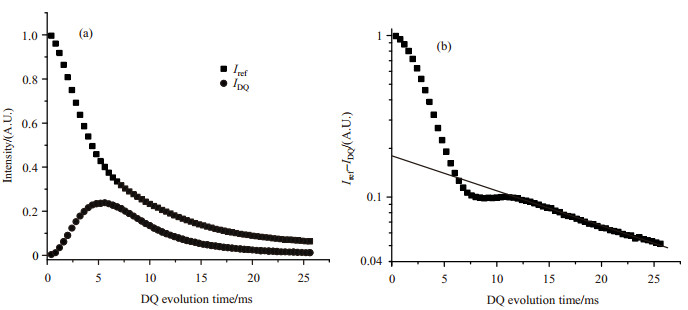
对图 5中1H NMR谱积分,可以得到质子信号强度随激发时间的变化如图 6(a)所示.图 6(a)中圆形为双量子信号IDQ随双量子演化时间的变化,方形为参考信号Iref随双量子演化时间的变化.将Iref与IDQ之差与激发时间作图得到图 6(b),图中我们看到两种不同的弛豫行为:前半段信号弛豫较快,且信号以非指数形式弛豫,为交联链段的弛豫信号;后半段弛豫较慢,且信号以指数形式弛豫,为未交联链段的弛豫信号.由于未交联组分的非弹性缺陷所产生的信号会导致测量误差过大,因此我们需要扣除这部分的信号.在数据处理过程中,我们先选取了后半段数据进行拟合,拟合方程为(9)式,式中y由Iref与IDQ作差所得.拟合得到的非弹性组分含量f及质子横向弛豫时间T2, tail见表 2.
| $ y = f\exp ( - 2{\tau _{{\rm{DQ}}}}/{T_{{\rm{2, tail}}}}) $ | (9) |
|
图 6 一个硫化时间为7 min的橡胶样品的1H DQ NMR实验. (a)双量子信号(IDQ)和参考信号(Iref)曲线;(b) Iref与IDQ的差异曲线(Iref–IDQ) Figure 6 1H DQ NMR of a rubber sample having a curing time of 7 min. (a) The DQ build-up (IDQ) and the reference (Iref) curves; (b) The difference (Iref-IDQ) curve |
| 表 2 1H DQ NMR的拟合参数及计算的Mc Table 2 The parameters used in the 1H DQ NMR data fitting and the yielded Mc values |
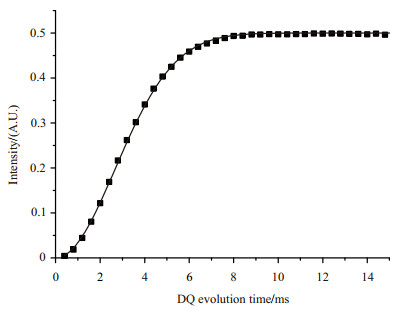
将拟合得到的f及T2, tail代入(4)式,可得到归一化后的DQ累积数据InDQ随双量子演化时间的变化,如图 7所示.由图 7可知,归一化的双量子信号随着双量子演化时间的变大而逐渐变大,最后到达一个平台.对图 7利用可用(5)式拟合可以得到残余偶极相互作用Dres,通过(6)式可计算交联点间的相对分子质量Mc,所有样品的Dres和Mc见表 2.
|
图 7 归一化的DQ曲线 Figure 7 The normalized DQ curve |
分析表 2中的数据我们发现,Mc随着硫化时间的增加先变小后变大.在拟合中我们发现,非弹性缺陷含量f随着硫化时间的增加先变小后变大,而质子横向弛豫时间T2, tail先变大后变小,转折点为硫化时间为20 min的胶料.非弹性缺陷包括悬垂链和溶胶等小分子,我们推测在硫化过程中,悬垂链反应形成了交联网络,溶胶等小分子则留在交联网络的空隙中,所以非弹性缺陷组分的含量f逐渐变小,而质子横向弛豫时间T2, tail变大.
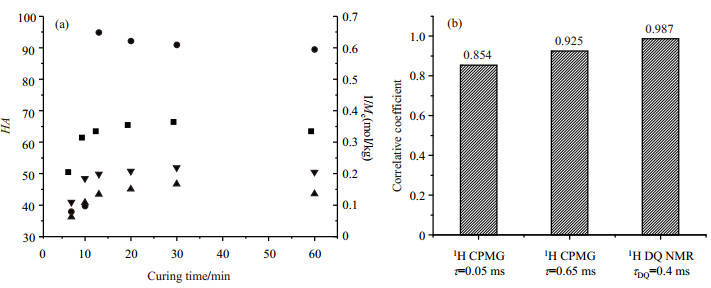
2.3 硬度与交联密度NMR测量值的相关性由于橡胶的交联密度大小会影响其力学性能,所以我们将交联密度NMR测量值Mc与橡胶的硬度进行了比较.图 8(a)为不同硫化时间下橡胶的硬度和Mc的倒数,方形表示橡胶的硬度的大小,圆形和三角形分别表示脉冲间隔时间τ分别为0.05 ms和0.65 ms时CPMG实验测得的Mc的倒数,倒三角形表示使用1H DQ NMR序列测得的Mc的倒数.由图 8(a)可知,随硫化时间的变大,1/Mc和硬度都呈现先变大后变小的趋势,说明硬度与橡胶的1/Mc的变化趋势相同.刘天琦等[29]也发现硬度随着Mc的变大而变小,并且两者近似为线性关系.为了比较交联密度NMR的测量值与硬度的相关性,我们利用(8)式计算了相关性系数.如图 8(b)所示,脉冲间隔时间为0.05 ms和0.65 ms的CPMG实验测得的橡胶交联密度与硬度的相关性系数为分别为0.854和0.925,1H DQ NMR测得的橡胶交联密度与硬度的相关性系数为0.987,高于CPMG实验的测量结果.
|
图 8 (a) 不同橡胶样品的邵氏硬度(HA, ■)与通过NMR测得的Mc的倒数(●1H CPMG,τ = 0.05 ms;▲1H CPMG,τ = 0.65 ms;▼1H DQ NMR)随硫化时间的变化;(b)橡胶交联密度NMR测量值与邵氏硬度的相关性系数 Figure 8 (a) Hardness (HA, ■) and 1/Mc values measured using NMR (●1H CPMG, τ = 0.05 ms; ▲1H CPMG, τ = 0.65 ms; ▼1H DQ NMR) change with the curing times; (b) Correlative coefficients between the sample hardness and the crosslink density |
我们计算了13个脉冲间隔时间下CPMG实验测量的交联密度与硬度相关性系数(见表 3).脉冲间隔时间不同时,CPMG实验测得的交联密度与硬度的相关性存在较大的差异;脉冲间隔时间为0.45 ms时,r最大,为0.954,但仍然低于1H DQ NMR的测量结果.这是因为1H DQ NMR是通过测量双量子相干的激发效率来测量橡胶的交联密度,激发效率取决于交联网络体系的残余偶极相互作用Dres,物理交联和化学交联都会使得体系的残余偶极相互作用增大,所以1H DQ NMR测得的是化学交联和物理交联的总和.由于物理交联和化学交联都会增强橡胶的力学性质,所以硬度是物理交联和化学交联共同作用的结果.因此1H DQ NMR的测量结果和硬度都能在一定程度上比较好的反映橡胶的交联情况,相关性系数很高.对于CPMG实验来说,测得的交联密度与硬度之间的相关性系数较低,这可能是因为CPMG实验只针对橡胶中某一部分高分子链段质子信号的“选择性”观察.
| 表 3 不同脉冲间隔时间下,CPMG实验测得的同组橡胶交联密度与硬度的相关性系数.脉冲间隔时间(τ)为:0.05 ms、0.10 ms、0.15 ms、0.20 ms、0.25 ms、0.30 ms、0.35 ms、0.40 ms、0.45 ms、0.50 ms、0.55 ms、0.60 ms和0.65 ms Table 3 Correlative coefficients between sample hardness and the crosslink density measured with CPMG experiments at different interval times between the pulses for the same rubber. The interval times between the pulses were 0.05 ms, 0.10 ms, 0.15 ms, 0.20 ms, 0.25 ms, 0.30 ms, 0.35 ms, 0.40 ms, 0.45 ms, 0.50 ms, 0.55 ms, 0.60 ms and 0.65 ms, respectively |
在低场NMR谱仪上,由于磁体通常不配备匀场系统,典型的磁场不均匀性在100 Hz以上.过高的磁场不均匀性常常会导致1H DQ NMR测量产生较大的误差,而CPMG实验可以很好的“消除”磁场不均匀性对1H横向弛豫带来的影响,因此比较适合在磁场均匀性差的低场NMR谱仪上使用.本节将探讨如何改进常规的CPMG实验,提高其测量值与硬度的相关性,使该序列能够在低场NMR谱仪上实现对橡胶样品交联密度的可靠测量.
根据上述讨论,我们发现在CPMG实验中,Mc对序列脉冲间隔时间存在依赖性,这是因为对于CPMG实验来说,使用特定脉冲间隔时间可能意味着对材料中某一部分高分子链段质子信号的“选择性”观测.因此我们认为如果将不同脉冲间隔时间下CPMG实验获得的质子横向弛豫曲线进行特定方式的叠加,有可能使叠加后的质子横向弛豫曲线中包含多种甚至所有高分子链段的运动信息.通过对叠加后的质子横向弛豫曲线进行分析,可能获得更为精确的交联密度测量值,改善上述常规CPMG实验的不足.基于这一考虑,我们对由不同脉冲间隔时间下CPMG实验获得质子横向驰豫曲线在高斯加权后进行了叠加.通过对叠加后的质子横向弛豫曲线进行分析,实现了对橡胶样品交联密度的更为可靠和精准的测量.
2.4.1 不同CPMG实验测得的质子横向驰豫曲线的高斯加权我们利用(10)式的高斯分布函数[31]计算不同脉冲间隔时间时CPMG实验测量数据的权重因子:
| $ f(x) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\exp \left[{-\frac{{{{(x-\mu )}^2}}}{{2{\sigma ^2}}}} \right] $ | (10) |
其中σ为分布宽度,μ为分布中心.
不同脉冲间隔时间下叠加的质子横向弛豫曲线可按(11)式进行累加:
| $ Y(t) = {q_1}{y_1}(t) + {q_2}{y_2}(t) + \cdots + {q_n}{y_n}(t) $ | (11) |
式中:qn为质子横向驰豫数据所对应的权重因子;yn为质子横向驰豫;Y为累加后的质子横向弛豫.
我们以σ = 0.15、μ = 0.45的高斯分布为例来展示数据的处理过程.由(10)式可以得到不同脉冲间隔时间CPMG质子横向驰豫数据的权重因子,图 9(a)展示了计算得到的权重因子:CPMG实验中脉冲间隔时间为0.45 ms时权重最大(0.143);为0.05 ms时权重最小(0.004).利用(11)式可以得到加权后的质子横向驰豫数据,我们以硫化7 min的橡胶为例绘制了图 9(b),方形和圆形表示CPMG脉冲间隔时间为0.05 ms和0.65 ms时CPMG实验测得的横向驰豫曲线,三角形表示高斯加权后的质子横向驰豫曲线.我们发现通过高斯权重因子的加权,质子横向驰豫曲线处于τ为0.05 ms和0.65 ms测试结果之间.

|
图 9 (a) 1H CPMG实验所用脉冲间隔时间(τ)按高斯分布后的加权因子.该高斯分布的中心μ= 0.45、分布宽度σ= 0.15;(b)常规和高斯加权的1H CPMG横向驰豫曲线.常规1H CPMG横向驰豫曲线的脉冲间隔时间(τ)是0.05 ms和0.65 ms.高斯加权的1H CPMG横向驰豫曲线由13条不同脉冲间隔时间(τ)的1H CPMG横向驰豫曲线乘以相应的高斯加权因子后加和而得 Figure 9 (a) The Gaussian distribution of the weighting factors at the interval time between the pulses (τ) in the 1H CPMG experiments with μ= 0.45 and σ= 0.15; (b) The usual 1H CPMG and Gaussian-weighted 1H CPMG decay curve. The usual 1H CPMG relaxation curves were obtained in the CPMG experiments having the interval times between the pulses (τ) of 0.05 ms and 0.65 ms. The Gaussian-weighted 1H CPMG relaxation curve were the summation of thirteen CPMG curves. Each CPMG curve was multiplied by the corresponding weighting factor before the summation |
我们对硫化7 min、10 min、13 min、20 min、30 min和60 min的橡胶的质子横向驰豫曲线重复上述的高斯加权,并进行交联密度的拟合,拟合的数据见图 10.我们发现,高斯加权得到的1/Mc与硬度的趋势十分接近.此外,交联密度NMR测量值与硬度的相关性系数r为0.991,超过了1H DQ NMR得到的相关性系数,说明经过施加高斯分布的权重因子,可以大幅度提高交联密度1H CPMG测量值与硬度的相关性.值得一提的是,由于1H DQ NMR序列的测试时间为34 min,单个CPMG实验的测试时间为16 s,13个具有不同脉冲间隔时间的CPMG实验的总测试时间大约3.5 min,因此高斯加权的1H CPMG的实验时间仅为1H DQ NMR的1/10.

|
图 10 橡胶邵氏硬度(HA)与两种不同NMR方法(高斯加权的1H CPMG NMR和1H DQ NMR)测得的Mc的倒数 Figure 10 Rubber hardness (HA) and the 1/Mc values obtained from Gaussian-weighted 1H CPMG and 1H DQ NMR methods |
高斯分布的分布中心μ和分布宽度σ会对权重因子产生很大的影响.因此我们接下来研究μ和σ的取值对上述方法获得的Mc的影响.我们首先将σ固定为0.15,μ选取了0.05、0.20、0.45及0.65,对上文测试胶料的质子横向弛豫进行高斯分布加权拟合,计算得到的交联点间的相对分子质量Mc见表 4,表中还给出了高斯加权后得到的橡胶交联密度与硬度的相关性系数.
| 表 4 不同高斯分布中心下,通过高斯加权的1H CPMG拟合得到的橡胶的Mc及交联密度与硬度的相关性系数r Table 4 Mc and correlative coefficients (r) between the hardness and crosslink density fitted by Gaussian-weighted 1H CPMG relaxation curves at different distribution center |
从表 4的数据可以发现,分布中心μ不同时,Mc和r都不同.当μ由0.05增加至0.65时,r先变大后变小;当μ为0.45时,r为0.991,此时相关性最好.说明分布中心μ对交联点间的相对分子质量Mc有很大的影响,当选择合适的分布中心时,可以很大程度上提高CPMG实验的测试结果.
接着我们研究σ的取值对Mc的影响,我们将分布中心μ固定为0.45,σ选取了0.01、0.10、0.15、及0.50,对上文测试胶料的质子横向弛豫进行高斯分布加权拟合,计算得到的交联点间的相对分子质量及交联密度与硬度的相关性系数见表 5.从表 5的数据可以发现,分布宽度σ不同时,Mc和r都不同.当σ由0.01增加至0.5时,r逐渐变大;当σ为0.15时,r为0.991;σ继续变大时,r几乎不变.
| 表 5 不同高斯分布宽度时,通过高斯加权的1H CPMG拟合得到橡胶的Mc及交联密度与硬度的相关性系数r Table 5 Mc and correlative coefficients (r) between the hardness and crosslink density fitted by Gaussian-weighted 1H CPMG relaxation curves at different distribution width |
综上所述,高斯分布中心和分布宽度对Mc的拟合有一定的影响,选取适当的分布中心和分布宽度可以提高高斯加权的1H CPMG实验测得的橡校交联密度与硬度的相关性.对于本文研究的硫化橡胶而言,分布中心μ为0.45、分布宽度σ为0.15时,测得的橡校交联密度与硬度的相关性最好,为0.991.
3 结论本文提出了一种通过1H CPMG实验快速和精确测量橡胶Mc的方法.该方法通过对不同脉冲间隔时间下CPMG实验测得的质子横向驰豫曲线进行高斯加权求和,改善了传统CPMG方法测得的Mc对脉冲间隔时间依赖性较大的缺点,大幅提升了天然橡胶交联密度NMR测量值与材料硬度的相关性.与1H DQ NMR方法相比,通过本文方法测量获得的天然橡胶交联密度材料硬度相关性相当或更佳.同时,本文方法比1H DQ NMR更为高效,整体测量时间缩短为1H DQ NMR实验时间的1/10.
| [1] |
WANG Z L. Crosslinking density of rubbers and the method of determination[J].
World Rubber Industry, 1998, 25(4): 41-46.
王作龄. 橡胶的交联密度与测定方法[J]. 世界橡胶工业, 1998, 25(4): 41-46. |
| [2] |
ZHU R P, ZHOU B, YANG J, et al. Effect of crosslinking density on dynamic performance of natural rubber[J].
Special Purpose Rubber Products, 2009, 30(1): 43-45.
朱闰平, 邹波, 杨军, 等. 交联密度对天然橡胶动态性能的影响[J]. 特种橡胶制品, 2009, 30(1): 43-45. |
| [3] | STUDEBAKER M L. Lithium aluminum hydride analysis of sulfur-cured vulcanizates[J]. Rubb Chem Tech, 1970(43): 624-643. |
| [4] | SCHLOGL S, TRUTSCHEL M L, CHASSÉ W, et al. Entanglement effects in elastomers:macroscopic vs microscopic properties[J]. Macromolecules, 2014, 47(9): 2759-2773. DOI: 10.1021/ma4026064. |
| [5] | MULLINS L. Determination of degree of crosslinking in natural rubber vulcanization. Part Ⅰ[J]. J Polym Sci, 1956, 19(92): 225-236. DOI: 10.1002/pol.1956.120199201. |
| [6] | LITVINOV V M, Dias A A. Analysis of network structure of UV-cured acrylates by 1H NMR relaxation, 13CNMR spectroscopy and dynamic mechanical experiments[J]. Macromolecules, 2001, 34(12): 4051-4059. DOI: 10.1021/ma010066u. |
| [7] | GENNES P G D. Reptation of a polymer chain in the presence of fixed obstacles[J]. J Chem Phys, 1971, 55(2): 572-579. DOI: 10.1063/1.1675789. |
| [8] | KUHN W, PEREGI E, FEI Z, et al. Network dynamics of crosslinked polymers-crosslinking, filler and aging characterized by NMR parameters[J]. Mater Res SocSympProc, 1991, 33(1): 217-223. |
| [9] | KUHN W, BARTH P, HAFNER S, et al. Material properties imaging of cross-linked polymers by NMR[J]. Macromolecules, 1994, 27(20): 5773-5779. DOI: 10.1021/ma00098a035. |
| [10] | FEDOTOV V D, Schneider H. Structures and dynamics of bulk polymers by NMR-methods[M]. Springer-Verlag: 1989. |
| [11] |
ZHAO S Y, WANG Y Y, ZHANG R C, et al. Low-field NMR studies on the structure and dynamics of nanocompositehydrogels[J].
Chinese J MagnReson, 2014, 31(2): 172-184.
赵守远, 王媛媛, 张荣纯, 等. 低场固体NMR研究纳米复合凝胶结构与动力学[J]. 波谱学杂志, 2014, 31(2): 172-184. |
| [12] | GAO Y, ZHANG R C, LV W F, et al. Critical effect of segmental dynamics in polybutadiene/clay nanocomposites characterized by solid state 1H NMR spectroscopy[J]. J Phys Chem C, 2014, 118(10): 5606-5614. DOI: 10.1021/jp5013472. |
| [13] | SAALWÄCHTER K. Proton multiple-quantum NMR for the study of chain dynamics and structural constraints in polymeric soft materials[J]. Prog Nucl Mag Res Sp, 2007, 51(1): 1-35. DOI: 10.1016/j.pnmrs.2007.01.001. |
| [14] | HAHN E L. Spin Echoes[J]. Phys Rev, 1950, 80: 580-594. DOI: 10.1103/PhysRev.80.580. |
| [15] | CARR H Y, PURCELL E M. Effect of diffusion on free precession in nuclear magnetic resonance experiments[J]. Phys Rev, 1954, 94(3): 630-638. DOI: 10.1103/PhysRev.94.630. |
| [16] | MEIBOOM S, GILL D. Modified spin-echo method for measuring nuclear relaxation times[J]. Rev Sci Instrum, 2004, 29(8): 688-691. |
| [17] | BAUM J, PINES A. NMR studies of clustering in solids[J]. J Am Chem Soc, 1986, 108(24): 7447-7454. DOI: 10.1021/ja00284a001. |
| [18] | SAALWÄCHTER K, KLÜPPEL M, LUO H, et al. Chain order in filled SBR elastomers:a proton multiple-quantum NMR study[J]. Appl Magn Reson, 2004, 27(3, 4): 401-417. |
| [19] | SAALWÄCHTER K, ZIEGLER P, SPYCKERELLE O, et al. 1H multiple-quantum nuclear magnetic resonance investigations of molecular order distributions in poly (dimethyl siloxane) networks:Evidence for a linear mixing law in bimodal systems[J]. J Chem Phys, 2003, 119(6): 3468-3482. DOI: 10.1063/1.1589000. |
| [20] | SAALWÄCHTER K. 1H multiple-quantum nuclear magnetic resonance investigations of molecular order in polymer networks.Ⅱ. Intensity decay and restricted slow dynamics[J]. J Chem Phys, 2004, 120(1): 454-64. DOI: 10.1063/1.1630561. |
| [21] | SAALWÄCHTER K, AND B H, LÓPEZMANCHADO M A. Chain order and cross-link density of elastomers as investigated by proton multiple-quantum NMR[J]. Macromolecules, 2005, 38(38): 9650-9660. |
| [22] | HEUERT U, KNÖRGEN M, MENGE H, et al. New aspects of transversal 1H NMR relaxation in natural rubber vulcanization[J]. Polym Bull, 1996, 37(4): 489-496. DOI: 10.1007/BF00556810. |
| [23] | SIMON G, BIRNSTIEL A, SCHIMMEL K H. Network characterization of end-linked poly(dimethyl siloxane) by 1H NMR spin-spin relaxation[J]. Polym Bull, 1989, 21(2): 235-241. |
| [24] | FRY C G, LIND A C. Determination of crosslink density in thermoset polymers by use of solid-state proton NMR techniques[J]. Macromolecules, 1988, 601(2): 921-929. |
| [25] | WHITTAKER A K, BREMNER T, ZELAYA F O. The effect of field inhomogeneous and molecular diffusion on the NMR transverse relaxation behavior of polymer melts[J]. Polymer, 1995, 36(11): 2159-2164. DOI: 10.1016/0032-3861(95)95291-8. |
| [26] | HILL L W. Calculation of crosslink density in short chain networks[J]. Prog Org Coat, 1997, 31(3): 235-243. DOI: 10.1016/S0300-9440(97)00081-7. |
| [27] | GOTLIB Y Y, LIFSHITZ M I, SHEVELEV V A, et al. The influence of the chemical crosslinking network on the spin-spin relaxation of crosslinked and swelling polymer systems[J]. Polymer Science U.s.s.r, 1976, 18(10): 2630-2636. DOI: 10.1016/0032-3950(76)90192-1. |
| [28] | KLUPPEL M, MENGE H, SCHMIDT H, et al. Influence of preparation conditions on network parameters of sulfur-cured natural rubber[J]. Macromolecules, 2001, 34(23): 8107-8116. DOI: 10.1021/ma010490v. |
| [29] |
LIU T Q, FANG Q H, HU Z L, et al. Study on relationship between cross-linking density and crystallization characteristic of gutta-percha rubber[J].
China Rubber Industry, 2013, 60(10): 593-597.
刘天琦, 方庆红, 胡之朗, 等. 杜仲橡胶硫化胶交联密度与结晶性能关系研究[J]. 橡胶工业, 2013, 60(10): 593-597. DOI: 10.3969/j.issn.1000-890X.2013.10.003. |
| [30] | BREMNER T, RUDIN A. The effect of degassing on the measurement of transverse relaxation times in molten polymers[J]. J Poly m Sci B, 1996, 34(11): 1893-1902. DOI: 10.1002/(ISSN)1099-0488. |
| [31] | MITROBOLSKY. Gaussian Distribution[M]. Beijing: Science Press, 1959. |
 2018, Vol. 35
2018, Vol. 35 
