2. 东北大学 中荷生物医学与信息工程学院, 辽宁 沈阳 110169
2. Sino-Dutch biomedical and information engineering school, Northeastern University, Shenyang 110619, China
核磁共振成像(又称磁共振成像,Magnetic Resonance Imaging, MRI)是一种利用人体组织内进动的核自旋(通常为氢核)在磁场与射频脉冲作用下发生章动之后产生射频信号,通过电脑将得到的射频信号进行处理而得到人体信息的一种医疗影像技术[1].由于其检测方便快捷、对人体无害等优点,MRI扫描仪已逐渐在各大、小医院普及.
在成像过程中,为了得到一幅磁共振影像,需要对被试身体的各部位进行空间定位,这是通过在不同方向施加梯度场实现的[2].而梯度场由梯度线圈产生,梯度线圈中的电流随时间快速切换,会在其周围的金属体内激发出变化的涡旋电场,进而导致金属体内闭合的回路中产生对原来的梯度电流起抑制作用的感生电流,也就是我们所说的涡流.涡流的存在不仅会使梯度场的波形发生畸变,同时也会严重的影响成像速度和图像质量[3, 4],因此对成像过程中涡流场的测量对后续的涡流补偿甚至消除具有重要的研究和应用价值[5].
国内外学者已经提出了多种计算和降低涡流的办法,例如有限差分时域法(Finite Difference Time Domain,FDTD)[6],但这种方法因为需要进行大量的计算所以要耗费很长的时间.还有有限元法(Finite Element Method,FEM)[7]和多层积分法(Multilayer Integral Method,MIM)[8],但这两种算法在远场边界条件下的计算结果通常不能满足要求,因此本文提出了一种利用电磁感应原理以及信号采集和处理技术测量磁共振磁场涡流的方法,实验证明该方法可以简单有效的对磁体产生的涡流场进行测量.
1 理论 1.1 涡流的产生和影响在成像过程中,梯度系统通过在梯度线圈中通入快速变换的电流在X、Y、Z 3个方向产生3路快速切换的线性梯度场.由于梯度线圈被各种导电材料所包围,当梯度线圈中的电流快速切换方向时,产生的梯度磁场就会在其周围的导电材料中激发出变化的涡旋电场,进而导致金属闭合回路中产生抑制原梯度电流的感生电流,我们称之为涡流[9].由于涡流本身又产生随时间变化的磁场,其分布与梯度线圈所产生的磁场方向正好相反,因此涡流对梯度线圈产生的磁场具有削弱作用.涡流会随着梯度的强度及变化速率的增加而增加,当梯度强度达到它的平台值时,涡流就开始衰减.
涡流的存在一方面将引起图像几何结构失真[10, 11].因为计算机重建图像时读取梯度频率和相位编码方向均采用线性插值算法[12],而涡流的存在使实际场强产生非线性变化,从而导致了信号投影空间错位.涡流越强,梯度场波形受影响越大,磁共振图像失真越严重.涡流的存在另一方面也会限制成像速度[13].梯度磁场切换率就是梯形上升沿的斜率.梯度磁场切换率越高,梯度电流强度上升越快,达到最强梯度场所需时间越短,成像速度越快.涡流的存在将导致梯度波形上升沿和下降沿拖长[14],限制成像系统的回波时间,从而影响成像速度.所以涡流的存在对图像的质量和成像速度都有影响[15, 16].
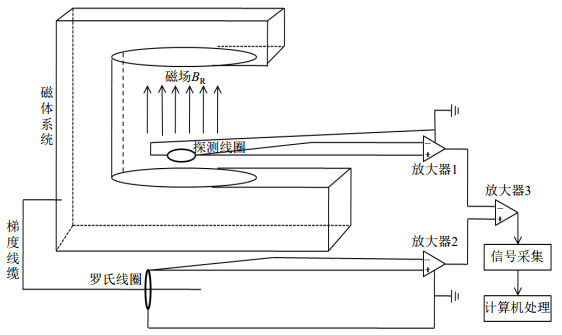
1.2 磁体涡流场测量装置的原理和设计 1.2.1 涡流场测量装置图 1是整个磁体涡流测量装置的示意图,实验中将探测线圈置于MRI扫描仪的磁场区域,同时将连接MRI主磁体系统与梯度系统的电缆垂直穿过罗氏线圈环形骨架的中心.在MRI扫描仪工作时,工作区域的实际磁场以及由梯度系统控制的梯度磁场变化会分别在探测线圈以及罗氏线圈中产生感生电动势,根据电磁感应定律可以计算出MRI扫描仪工作区域的梯度磁场(实际梯度磁场)与梯度系统控制的梯度磁场(理想梯度磁场).假设理想梯度磁场为BI,由于涡流产生的磁场(涡流场)为BE,实际梯度磁场BR=BI+BE.将理想梯度磁场与实际梯度磁场进行相减就可以得到涡流场的波形.实验中通过探测线圈和罗氏线圈采集到的是电压信号,后续将通过程序对电压数据进行数值积分及其他必要的运算得到磁场随时间变化的数据及波形.
|
图 1 涡流场测量装置示意图 Figure 1 Schematic diagram of the eddy current field measurement device |
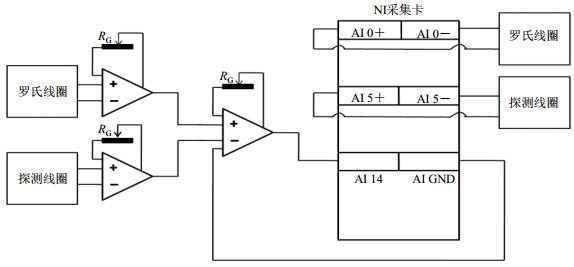
图 2为测量电路的示意图,在实验中采用3个相同的仪表放大器制作了一个减法器,通过外接一个电阻RG可以调节放大器的放大倍数.将罗氏线圈和探测线圈的信号分别接入到前两个放大器的输入端,为了保证实验的严谨性,在设计电路时还分别将罗氏线圈的信号和探测线圈的信号与通道AI 0以及通道AI 5相连,输入方式为差动输入,这样就可以得到罗氏线圈和探测线圈单独测量的信号,之后可以运用软件数据处理方法将两个信号直接进行相减得到测量涡流场的结果.
|
图 2 测量电路示意图 Figure 2 Schematic diagram of circuit measurement |
实验中数据采集的部分采用的是NI(National Instruments)公司的数据采集卡[17],将其安装在计算机上,采集卡通过一根其专有的数据连接线缆与外界相连,线缆的一端与采集卡相连,另一端与焊接在实验需要的电路板上的卡槽相连.每一个NI采集卡都有一个模数转换器(Analog Digital Converter, ADC),执行A/D转换、生成数字输出信号,测量和控制数字I/O信号.
1.2.2 实际梯度磁场BR的测量根据法拉第电磁感应定律,将一个n匝的闭合线圈置于被测磁场中,当通过它的磁通量发生变化时,就会在线圈内产生感生电动势[18],即:
| $ U(t) = - n{\rm{d}}\mathit{\Phi }/{\rm{d}}t = - nS{\mkern 1mu} {\rm{d}}[{B_{\rm{R}}}(t)]/{\rm{d}}t $ | (1) |
(1) 式中U(t)为感应电动势,Φ为通过线圈的磁通量的大小,n、S分别为线圈的匝数与面积.进一步可以得到线圈内的磁场强度随时间的变化规律:
| $ U(t){\rm{d}}t = - nS\, {\rm{d}}[{B_{\rm{R}}}(t)] $ | (2) |
将(2)式两边进行积分则可以得到实际梯度场BR(t)随时间变化的趋势:
| $ {B_{\rm{R}}}(t) = \int {U(t)} \, {\rm{d}}t/nS $ | (3) |
利用探测线圈可以得到由实际磁场产生的感应电压,进而计算得BR(t).探测线圈的制作比较简单,将200匝导线均匀绕制在一个非铁磁性的圆柱形结构上,线圈的半径为2.5 cm,整个线圈的面积约为0.4 m2,并在导线缠制一半时,抽出一个接头进行接地以消除共模干扰.
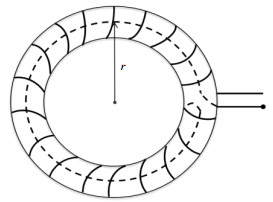
1.2.3 理想梯度磁场BI的测量实验中通过一种特制的线圈来实现理想梯度磁场BI的测量.这种线圈被称为Rogowski线圈(简称罗氏线圈),是一种依据法拉第电磁感应定律和安培环路定理、可以测量大电流的线圈[19, 20].罗氏线圈的基本结构如图 3所示,在非铁磁性的环形结构上均匀缠绕n匝线圈,并在内圈回绕一圈.由于小线匝彼此顺串沿着绕制线圈的循环方向便相当于形成了一匝大的线匝,而这是我们不希望的额外线匝,因为根据电磁感应定律可知,变化的磁场会在这一匝大线匝中产生感应电势,并且在测量中这是无法忽略的误差.在线圈内部回绕一匝线圈,由于这一线匝与小线匝相顺串,并且与大线匝反方向串联且回线与大线匝位于同一平面,因此垂直于罗氏线圈平面外的变化磁场在大线匝和回线中所产生的感应电势方向相反、大小近似相等而相互抵消,所以罗氏线圈的回绕结构能很好的补偿这种干扰电势从而不会影响被测电流的测量[21, 22].
|
图 3 罗氏线圈结构示意图 Figure 3 Structure diagram of Rogowski coil |
在测量时,将梯度系统连接的电缆垂直罗氏线圈环形骨架的中心,当交变电流通过时,会在罗氏线圈上感应出电压,大小与电流对时间的微分成正比:
| $ {B_{\rm{I}}}(t) = \int {{U_{\rm{I}}}(t)} \, {\rm{d}}t/nS $ | (4) |
其中UI(t)为梯度线圈在空间激发的磁场在罗氏线圈中产生的感应电动势,n、S为罗氏线圈的匝数和面积,利用(4)式进行计算可以得到理想梯度磁场随时间变化的趋势.
1.2.4 磁体涡流场BE的测量将上述BI(t)与BR(t)相减就可以得到由涡流产生的磁场BE(t).而实验中线圈测得的实际是电压,如何通过这两个电压得到最后的涡流场波形是最大的难点,将两种线圈测得电压除去对应的匝数与面积的乘积之后进行相减,再进行数值积分可以得到涡流场.可以理解为两个电压乘以一个特定的系数之后进行相减再进行数值积分.
在实际操作中转化为用两个放大器的放大倍数来实现将两个电压乘以特定系数这一过程.通过将两个放大器的放大倍数调节为相应的线圈匝数与线圈面积乘积的倒数之后对两个电压信号进行放大,再将两个放大后的信号接到第三个放大器的输入端进行相减,就可以实现两个信号相减,这时通过减法器得到的只是由于涡流场而产生的电压,之后再通过编好的程序对得到的电压UE(t)除去第三个放大器的放大倍数后进行数值积分就可以得到涡流场BE(t),后续再进行图像显示就可以得到实时的涡流场的波形.
2 实验方法 2.1 实验前的准备工作将实验装置制作完毕之后,为了保证实验结果的准确性,先对装置进行调试.软件方面,作者运用C#语言编写了一个信号采集程序来完成磁体涡流场的测量,并实时得到电压与磁场的波形显示.
2.2 现场测量实验中采用的MRI扫描仪的主磁体场强为0.35 T,实验中梯度磁场的周期为50 ms.打开事先设计好的磁体涡流测量程序,通过扫描100次之后求平均值的方法来减小误差,开始采集信号之前运用动态自校零的方法来对采集卡进行零点的校正,进一步来保证测量结果的准确性.
3 数据处理与分析实验中对梯度较强的两个点的涡流场进行了测量,采用了两种方法来对涡流场进行测量:一种是采用软件处理的方法分别将探测线圈和罗氏线圈的测量结果通过算法计算得到涡流场的波形;另一种则是直接对减法器得到的信号进行数据处理得到涡流场的波形,以下对两种方法得到的结果的具体分析.
3.1 罗氏线圈和探测线圈的测量结果实验中罗氏线圈与AI 0相连,探测线圈与AI 5相连.
对于罗氏线圈,无论其放在任何位置,只要梯度波形相同,测量结果就是相同的.图 4(a)为罗氏线圈测量的电压随时间的变化,图 4(b)是将电压经过计算得到的磁场随时间变化的趋势,因为罗氏线圈得到的电压与电流的微分成正比,所以其变化趋势也应该与电流的微分相同,在梯度波形的上升沿和下降沿处,由于加载的梯度要经过梯度放大器进行放大,瞬间就会产生一个非常剧烈的电流振荡,从而会导致波形如图 4(a)所示.从图 4(b)的部分放大图也可以看到在梯度波形的前沿和后沿都有一个“凸起”,这个“凸起”也是由于前面电流振荡导致的.从图 4还可以看出实验中制作的罗氏线圈的精确度很高,可以将电流的微小变化都探测到.

|
图 4 罗氏线圈测得的结果.(a)罗氏线圈测得的电压随时间的变化;(b)计算得到的磁场随时间的变化 Figure 4 Measured results of Rogowski coil. (a) Voltage variation with measurement time; (b) Magnetic field variation with measurement time |
图 5(a)和5(b)是探测线圈分别在Y轴正方向和负方向测得的电压按照前面的原理计算得到的磁场随时间的变化.梯度波形在上升和下降时,由于梯度电流的快速变化在系统中产生的涡流最为剧烈,体现在波形上就如图 5所示,使原本应该呈规则梯形走势的波形图变得十分平缓.

|
图 5 探测线圈测得的结果.(a)探测线圈在Y轴正方向30 cm处测得的磁场;(b)探测线圈在Y轴负方向30 cm处测得的磁场 Figure 5 Measured results of the detecting coil. (a) Magnetic field variation with measuring time at a distance of 30 cm from the positive direction of Y axis; (b) Magnetic field variation with measuring time at a distance of 30 cm from the negative direction of the Y axis |
由图 5可知对于实验中选定的两个位置,梯度磁场的大小非常相近,但是方向相反,与梯度磁场的性质(磁场中心对称的两点,磁场的大小相等而方向相反)一致.在实验中因为罗氏线圈测得的信号大小方向始终不变,但当把探测线圈从Y轴正方向移到Y轴负方向时,梯度磁场的方向是相反的,为了方便后面的减法器的工作,当将探测线圈从Y轴正方向换到Y轴负方向时,会将其与放大器的接线正负端进行调换来保证两个信号可以进行正确的相减.从图 5中的放大图可以看出在梯度磁场的上升沿和下降沿由于涡流的影响,形成了迟缓的曲线型而不是理想的梯度波形.
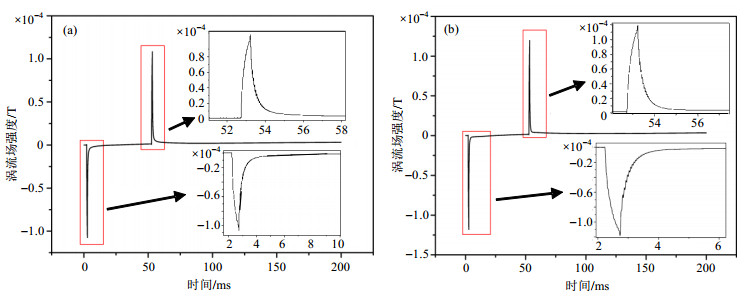
图 6为对前面的探测线圈和罗氏线圈测得的数据进行处理之后得到的涡流场的波形,图 6(a)和6(b)的波形大致相同,均在梯度前端与后端有一个比较明显的尖峰,这也是由于在梯度的上升沿和下降沿电流变化最快,所以涡流也最强.实验测得该实验条件下,涡流场的强度在10-4 T量级,大约是主磁场的0.1%.
|
图 6 经过数据处理后得到的涡流场波形.(a) Y轴正方向30 cm处涡流场; (b) Y轴负方向30 cm处涡流场 Figure 6 The eddy current field waveform obtained by data processing. (a) Eddy current field at a distance of 30 cm form the positive direction of Y axis; (b) Eddy current field at a distance of 30 cm form the negative direction of Y axis |
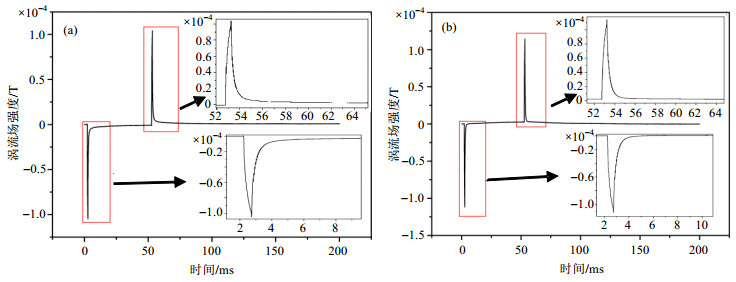
图 7是罗氏线圈和探测线圈的信号经过减法器之后测得的电压经处理后得到的结果,该结果已将减法器的放大因素考虑进去.通过图 7(a)和7(b)可以看到梯度波形的上升沿和下降沿涡流的强度越来越强,并且方向相反,随时间变化到后面逐渐趋近于0.这也很好的解释了涡流在梯度场快速上升和下降时越来越严重,从而影响了梯度场的快速切换.涡流场测量结果也在10-4 T量级,与上述通过算法计算得到的涡流场强度非常接近,这说明本文设计的磁体涡流场测量装置的测量结果准确、测量精度较高.
|
图 7 减法器测得的结果.(a) Y轴正方向30 cm处涡流场波形图;(b) Y轴负方向30 cm处涡流场信号波形图 Figure 7 Measured results by the subtractor. (a) Eddy current field waveform at a distance of 30 cm from the positive direction of Y axis; (b) Eddy current field signal waveform at a distance of 30 cm from the negative direction of Y axis |
MRI设备越来越广泛的应用于医院中,对于磁共振影像的精度以及成像速度的要求也越来越高.本文提出了一种原理简单、采集速度快的磁体涡流场测量方法,结合电磁感应定律,利用软、硬件结合的方法对永磁磁共振中的涡流场进行了测量,为后续的去涡流提供了参考.实验结果显示,该方法能够准确和精确的测量出磁共振磁体周围所产生的涡流,未来有一定的应用前景,但还需要进一步的改进与提高.
| [1] | DURBRIDGE G. Magnetic resonance imaging:fundamental safety issues[J]. J Orthop Sports Phys Ther, 2011, 41(11): 820-828. DOI: 10.2519/jospt.2011.3906. |
| [2] | NESSAIVER M. All you really need to know about MRI physics[M]. PA: Rittenhouse Book Distributors, 1996: 613-614. |
| [3] | KROOT J M B, EIJNDHOVEN S J L, VEN A A F. Eddy currents in a transverse MRI gradient coil[J]. J Eng Math, 2008, 62(4): 315-331. DOI: 10.1007/s10665-007-9208-9. |
| [4] |
ZHANG S Q. A detective method of mapping eddy currents[J].
Journal of Suzhou University (Natural Science), 2000, 16(4): 57-61.
章世全. 成像涡流的检测方法[J]. 苏州大学学报(自然科学版), 2000, 16(4): 57-61. |
| [5] | REESE T G, HEID O, WEISSKOFF R M, et al. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo[J]. Magn Reson Med, 2003, 49(1): 177-182. DOI: 10.1002/(ISSN)1522-2594. |
| [6] | LIU F, CROZIER S. An FDTD model for calculation of gradient-induced eddy currents in MRI system[J]. IEEE T Appl Supercon, 2004, 14(3): 1983-1989. DOI: 10.1109/TASC.2004.830609. |
| [7] | LI X, XIA L, CHEN W F, et al. Finite element analysis of gradient z-coil induced eddy currents in a permanent MRI magnet[J]. J Magn Reson, 2011, 208(1): 148-155. DOI: 10.1016/j.jmr.2010.10.017. |
| [8] | LOPEZ H S, FRESCHI F, TRAKIC A, et al. Multilayer integral method for simulation of eddy currents in thin volumes of arbitrary geometry produced by MRI gradient coils[J]. Magn Reson Med, 2014, 71(5): 1912-1922. DOI: 10.1002/mrm.v71.5. |
| [9] | AKRAM M S, TERADA Y, KEIICHIRO I, et al. Coupled circuit numerical analysis of eddy currents in an open MRI system[J]. J Magn Reson, 2014, 245(8): 1-11. |
| [10] | ZEVENHOVEN K C J, BUSCH S, HATRIDGE M, et al. Conductive shield for ultra-low-field magnetic resonance imaging:Theory and measurements of eddy currents[J]. J Appl Phys, 2014, 115(10): 103902. DOI: 10.1063/1.4867220. |
| [11] | MUELLER L, WETSCHEREK A, KUDER T A, et al. Eddy current compensated double diffusion encoded (DDE) MRI[J]. Magn Reson Med, 2015, 77(1): 328-335. |
| [12] | CHEN Y M, YE X J, HUANG F. A novel method and fast algorithm for MR image reconstruction with significantly under-sampled data[J]. Inverse Probl Imaging, 2017, 4(2): 223-240. |
| [13] | LECHNER-GREITE S M, MATHIEU J B, AMM B C. Simulation environment to predict the effect of eddy currents on image quality in MRI[J]. IEEE T Appl Supercon, 2012, 22(3): 4402104. DOI: 10.1109/TASC.2012.2186781. |
| [14] | 陈武凡. MRI原理与技术[M]. 北京: 科学出版社, 2012. |
| [15] |
SHEN J, NING R P, LIU Y, et al. A method for reducing eddy current induced by gradient coil[J].
Acta Physica Sinica, 2006, 55(6): 3060-3066.
沈杰, 宁瑞鹏, 刘颖, 等. 一种减小梯度线圈产生的涡流的方法[J]. 物理学报, 2006, 55(6): 3060-3066. DOI: 10.7498/aps.55.3060. |
| [16] | MA C, JIANG X H. A new eddy-current compensation method in MRI[J]. PIERS, 2007, 3(6): 874-878. |
| [17] |
GUO Z S, LI J Y. Measurement Technique, 2007(6): 50-52.
郭占山, 李建一. NI数据采集卡校准方法探讨[J]. 计量技术, 2007(6): 50-52. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jljs200706015&dbname=CJFD&dbcode=CJFQ |
| [18] | Michelson D. Faraday's laws of electromagnetic induction[J]. Physics Education, 1969, 4(6): 379. |
| [19] | 李维波. 基于Rogowski线圈的大电流测量传感理论研究与实践[D]. 武汉: 华中科技大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10487-2006039359.htm |
| [20] | HAN R Y, DING W D, WU J W, et al. A novel design of Rogowski coil for measurement of nanosecond-risetime high-level pulsed current[J]. Rev Sci Instrum, 2015, 86(3): 035114. DOI: 10.1063/1.4916094. |
| [21] | SAMIMI M H, MAHARI A, FARAHNAKIAN M A, et al. The rogowski coil principles and applications:A review[J]. IEEE Sen J, 2015, 15(2): 651-658. DOI: 10.1109/JSEN.2014.2362940. |
| [22] | PRAKASH N R, FLORA K, BABU R, et al. Design and development of rogowski coil sensors for eddy currents measurement on toroida l vessel[J]. J Fusion Energ, 2013, 32(2): 263-267. DOI: 10.1007/s10894-012-9562-0. |
 2018, Vol. 35
2018, Vol. 35 
