2. 上海卡勒幅磁共振技术有限公司, 上海 201614
2. Shanghai Colorful Magnetic Resonance Technology Co., Ltd., Shanghai 201614, China
磁共振成像(Magnetic Resonance Imaging, MRI)具有无电离辐射、多角度成像、多参数成像等特点,在临床诊断中具有重要的应用[1].但较长的扫描时间导致磁共振扫描易受运动伪影的影响;动态MRI时间分辨力较低;同时,单个患者扫描时间较长、成本较高,限制了MRI的进一步推广[2].为了加快扫描速度,提高扫描效率,近些年并行成像(Parallel Imaging, PI)技术和压缩感知(Compressed Sensing, CS)技术成为研究热点.
PI技术利用相控阵线圈灵敏度在空间位置上分布的不同,即线圈的灵敏度差异,进行空间编码来代替一部分梯度编码,减少所需要的k空间采集点数,达到提高成像速度的目的[3].目前应用最广的PI技术主要有SENSE(Sensitivity Encoding for Fast MRI)技术[4]和GRAPPA(Generalized Autocalibrating Partially Parallel Acquisitions)技术[5].SENSE技术是一种基于图像域的重建算法,需要预先知道线圈灵敏度的信息.GRAPPA技术是一种基于k空间域的重建算法,它以满足奈奎斯特采样定律要求的频率采集k空间中心数据作为自动校正数据(Auto-Calibration Signal, ACS),利用多通道k空间数据之间的相关性进行每个通道的k空间欠采行的填充,最后通过通道合并得到最终的无卷褶图像.相比于SENSE方法,GRAPPA有其独特的优势.SENSE方法要求知道精确的线圈灵敏度的空间分布,但是精确的灵敏度信息一般很难获得.而GRAPPA方法利用自校准方法,避免了校准扫描和PI扫描之间的不一致问题.
2006年,Michael Lustig等[6]提出了CS理论.CS是一种新的信号采集和信号恢复的理论,能大幅减少测量数据来重建信号和图像,因此在其诞生之初就被运用于MRI[6-9].CS方法以远低于奈奎斯特采样定律要求的采样频率对k空间进行随机欠采样,利用磁共振图像在变换域中的稀疏性,通过非线性重建算法消除图像中的非相干伪影,恢复欠采的k空间数据得到重建图像.
PI和CS技术都能通过减少k空间采集数据加速成像速度,目前已有一些将两种方法相结合以进一步加快磁共振成像速度的方法.这些方法大致可以分为两类:一类在重建过程中通过解一个能量函数最小化问题得到最终的重建图像,如SparseSENSE[10, 11],l1-SPIRiT[12, 13],SAKE[14]等;另一类在重建过程中采用分步重建的方式进行重建,先进行CS重建再进行PI重建或者先进行PI重建再进行CS重建,如CS-SENSE[15]、CS-GRAPPA[16-18]、PI-CS[19]等.
我们提出了一种新的结合PI与CS的方法,重建过程中顺序地采用GRAPPA重建和CS重建:先用GRAPPA重建部分k空间数据,再用CS恢复全k空间数据,单独完成每一通道的完整k空间数据重建后,再进行通道合并得到最终的重建图像.与现有的PI-CS方法不同的是,我们针对的是二维成像.与现有CS-GRAPPA不同的是,我们在重建过程中先进行GRAPPA重建再进行CS重建,为了满足PI所要求的采样数据的等间隔性和CS所要求的伪随机性,更好的发挥GRAPPA和CS的重建效果,我们设计了k空间局部采集模板,以该模板为单位,对k空间进行伪随机采集.这样做的好处是既能提高PI重建效率,又能使数据具有一定的随机性.同时在CS重建中我们引入部分保真的概念,根据预期的GRAPPA重建精度的不同,对重建行进行不同程度的保真.实验结果表明:该方法在保留图像细节的基础上能有效减少相干伪影.
1 基本理论 1.1 GRAPPA和CSGRAPPA是一种常用的基于k空间域的重建方式.它的基本假设是k空间中某一行数据可以通过其邻近行数据线性叠加得到.2005年,Wang等[20]提出多列多行插值(Multicolumn Multiline Interpolation, MCMLI)改进了GRAPPA重建方法,提高了图像重建质量.公式表示如下:
| $ {S_j}({k_y} - m\Delta {k_y}, {k_x}) = \sum\limits_{l = 1}^L {\sum\limits_{b = - {N_a}}^{{N_b}} {\sum\limits_{h = - {H_l}}^{{H_r}} {n(l, b, h){S_l}({k_y} + bR\Delta {k_y}}, {k_x} + h\Delta {k_x})} } $ | (1) |
(1) 式中,kx、ky表示k空间坐标;Δk表示k空间采样间隔;j代表第j个通道;Sj表示第j个通道采集的k空间数据;m是一个整数,R表示加速因子,m=1, 2, L, R-1;L表示线圈通道数;Na表示在重建数据上方的block数;Nb表示在重建数据下方的block数;Hl表示重建数据左边的相邻列;Hr表示重建数据右边的相邻列;n表示对应的系数.一个Block定义为单一采样行加上它邻近的(R-1)个欠采行,Δky=2π/FOV,是最小的k空间间隔,FOV(Filed of View)为观察视野.为了填充欠采行,我们需要在该欠采行邻近的block中找实际采样行数据,用实际采样行数据乘上对应的系数线性叠加得到欠采行数据.而对应的系数可以通过对ACS数据的拟合来得到,如(2)式;根据算出的系数,GRAPPA填充出每个线圈中缺失的k空间数据,在图像域进行图像合并,得到最终的重建图像.
| $ S_j^{ACS}({k_y} - m\Delta {k_y}, {k_x}) = \sum\limits_{l = 1}^L {\sum\limits_{b = - {N_a}}^{{N_b}} {\sum\limits_{h = - {H_l}}^{{H_r}} {n(l, b, h){S_l}({k_y} + bR\Delta {k_y}}, {k_x} + h\Delta {k_x})} } $ | (2) |
CS是用凸优化算法在采集数据的一致性和图像的稀疏性中进行约束求解,重建的能量函数可以表示为:
| $ \arg {\min _{\hat x}}||\Psi \hat x|{|_1} + \lambda ||{F_u}\hat x - y||_2^2 $ | (3) |
其中
在采样方式的选择上,如果选择完全偏向于PI的等间隔采样方式,那么就无法满足CS重建所要求的随机性;如果选择完全偏向于CS的伪随机采样方式,则在GRAPPA重建中只能重建非常有限的相位编码行.为了兼顾PI所要求的等间隔性和CS所要求的随机性,我们设计了一种局部等间隔的采集模板,并用该模板随机采集k空间.即根据既定的采样率设计合适的等间隔采样模板,然后将此模板根据k空间能量分布进行伪随机采样,同时以满足奈奎斯特采样定律要求的采样频率采集k空间中心的数据作为GRAPPA重建中的ACS数据.图 1显示的是矩阵大小为(320×320)的采样模板,频率编码方向全采,相位编码方向欠采,局部采样模板采用加速因子R=3.此模板ACS行为22行,实际采样行为96行,总采样率为30%.

|
图 1 局部R=3等间隔模板随机放置的采样方式 Figure 1 Sampling strategy by local template with R=3 |
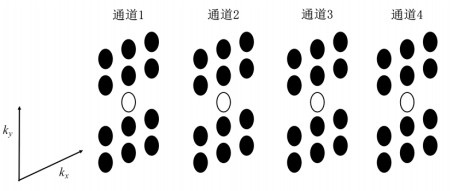
重建过程主要包括GRAPPA重建和CS重建两步,采样模板如图 1所示.用k空间中心的ACS数据对特定的重建模式(这种重建模式跟采样模板匹配)进行通道系数计算,用该系数分别填充每个通道的部分k空间数据,这里我们使用三列四行插值进行FD(Frequency Descrimination)-GRAPPA重建[21].在用ACS数据计算重建系数时,去掉k空间中心(N×N)的数据.如图 2所示为4通道线圈用三列四行重建k空间欠采点的模型图.黑色的点表示k空间采集的数据点,白色的点表示欠采点,重建通道1中所示欠采数据点,要分别在各个通道两维邻域内找距离欠采行数据最近的四行实际采样行,用三列四行插值(图中所有的黑色的点)重建第一个通道的欠采数据.在利用GRAPPA重建k空间时,我们不仅重建局部模板中的k空间数据,当模板间距较小时,也重建模板之间的k空间数据;根据实际采集位置得到一个较优的重建模式,再利用ACS数据计算该重建模式的系数,重建部分的k空间数据.
|
图 2 4通道线圈用三列四行插值重建欠采数据点模型图 Figure 2 The basic reconstruction for GRAPPA using 3-column 4-line interpolation |
在GRAPPA填充了部分欠采行数据之后,我们用CS恢复全k空间数据.在CS重建过程中,我们在(3)式中加入新的约束项,用以约束GRAPPA的重建k空间数据,主要依据是真实采集数据和GRAPPA重建数据的保真要求应有所区别,能量函数可以表示为:
| $ \arg {\min _{\hat x}}||\Psi \hat x|{|_1} + \lambda [||{F_u}\hat x-y||_2^2 + ||{\bf{W}}({F_g}\hat x-{y_G})||_2^2] $ | (4) |
其中,W是GRAPPA重建数据用于保真的相对权重矩阵,针对不同的GRAPPA重建行,赋予不同的保真权重,Fg表示表示傅里叶变换后GRAPPA重建的那部分数据,yG表示GRAPPA重建出的k空间的数据.
1.3.3 GRAPPA重建误差计算及保真权重的确定在重建k空间不同欠采行的数据时,依据实际采集行来得到重建模式.在利用ACS数据计算该重建模式系数的同时,也可以根据已有的ACS数据计算此重建模式的重建误差,考虑到k空间能量分布的特点,我们定义误差计算公式为:
| $ error = \sum\limits_{i = 1}^N {\left( {\frac{{|{I_{0i}} - {I_i}|}}{{|{I_{0i}}|}} \times \frac{{|{I_{0i}}|}}{{\sum\limits_{i = 1}^N {|{I_{0i}}|} }}} \right)} = \sum\limits_{i = 1}^N {\frac{{|{I_{0i}} - {I_i}|}}{{\sum\limits_{i = 1}^N {|{I_{0i}}|} }}} $ | (5) |
其中Ii表示重建的k空间数据点,I0i表示与之对应的ACS数据点的实际值,N表示用这种特定的重建模式重建的数据点的总数,
为了研究此误差跟用该重建模式重建k空间欠采数据的误差之间的关系,我们进行了数据实验.以12通道线圈(320×320)质子密度加权数据为例,FOV为200 mmx200 mm,层厚(Slice Thickness)为4 mm,回波时间(Echo Time, TE)为17 ms,重复时间(Repetition Time, TR)为3 000 ms,分辨率(Resolution)为0.62 mmx0.62 mm,我们设计R = 3的等间隔局部采样模板,对全k空间进行伪随机欠采,保证总采样率约为30%.
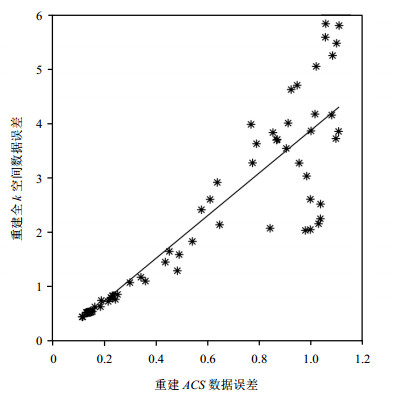
图 3显示的是第一个通道用不同重建模式重建全k空间数据和ACS数据的误差图,相关系数r = 0.89,其中相关系数计算如下:
| $ r = \frac{{\sum\limits_{i = 1}^n {({x_i} - \bar x)({y_i} - \bar y} )}}{{\sqrt {\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{({y_i} - \bar y)}^2}} } }} $ | (6) |
|
图 3 质子密度数据第一个通道重建全k空间数据和重建ACS数据的误差图 Figure 3 The error relationship between the whole k space data and the ACS data reconstructed for the first channel of the spin density-weighted brain data |
由此可知,可以对ACS数据的各种重建模式误差进行计算,作为对k空间中高频欠采区域的相同重建模式误差的估计.
计算得到不同重建模式的重建误差之后,在CS重建中对其进行部分保真.k空间中心能量大信噪比高,k空间外围能量小信噪比低,因此即使用同一种重建模式对欠采数据进行重建,在重建距离k空间中心近的欠采行时对应的重建误差小,重建距离k空间中心较远的欠采行时对应的重建误差较大.由此,我们确定CS重建中的相对保真值为:
| $ W(r) = {{\rm{e}}^{ - {{\left[{\frac{{error}}{{{k_1}}}(1 + \frac{1}{{{k_2}}} \times \frac{{2|r|}}{{{N_p}}})} \right]}^2}}} $ | (7) |
其中r表示要重建的特定行相对于中心的坐标,Np表示相位编码的总步数.k1和k2是自定义参数,对于不同实验数据,k1和k2的值可能不同.对于一些误差很大的重建模式的重建行,保真值置为0.
2 实验方法使用西门子TRIO 3T的超导MRI扫描系统,用T1加权数据和T2加权数据进行实验.两组数据频率编码方向都2倍过采,先对频率编码进行隔行采样,得到矩阵大小分别为(320×320)和(324×320)的数据,作为我们的全采数据.在数据欠采时,相位编码方向用我们所设计的R = 3的等间隔的局部模板,总采样率约为30%,其中k空间中央采22行作为ACS数据.我们将重建结果与现有的CS-GRAPPA算法进行比较.在CS-GRAPPA算法先等间隔(R = 2)采样,再以54%的采样率进行采样,同时采集k空间中心22行数据作为GRAPPA重建的ACS数据.保证总采样率约为30%.CS重建中使用Split Bregman算法[22],在全变分(Total Variation, TV)域进行稀疏约束.
其中T1加权数据扫描线圈为12通道头部线圈,扫描参数为:FOV为220 mmx220 mm,层厚为5 mm,TE为3.11 ms,TR为120 ms,空间分辨率为0.69 mmx0.69 mm.重建过程中,N = 10,CS参数外循环为20,内循环次数为5,参数λ为23,μ为9,部分保真权重中k1 = 0.2、k2 = 5 500,误差大于0.4的重建模式对应的重建行在部分保真时保真值置为0.
T2加权数据扫描线圈也为12通道头部线圈,扫描参数为:FOV为200 mmx200 mm,层厚为4 mm,TE为93 ms,TR为6 000 ms,分辨率为0.62 mmx0.62 mm.重建过程中,N = 10,CS参数外循环为20,内循环次数为5,λ为13,μ为6,部分保真权重中k1 = 0.2、k2 = 500,误差大于0.3的重建模式对应的重建行在部分保真时保真值置为0.
为了对图像进行定量评价,本文使用峰值信噪比(Peak Signal-to-Noise, PSNR)、结构相似性(Structure Similarity, SSIM)[23]进行图像评估.其中PSNR是从像素值角度对图像整体进行评估,SSIM是从图像结构角度进行评估.
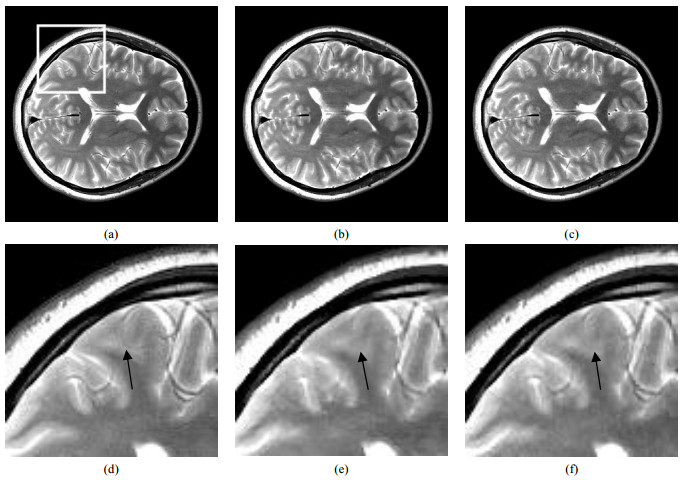
3 结果与讨论图 4和图 5分别展示了T1加权数据和T2加权数据的重建结果.图(a)为全采数据的重建图像;图(b)为已有的CS-GRAPPA方法重建图;图(c)使用本文提出的方法重建图;图(d)~(f)分别为局部放大图.从重建图和局部放大图中我们能看出,相比于现有的CS-GRAPPA算法方法,我们所提出的方法能减少随机伪影,同时细节也更清楚,如放大图中箭头指示的细小血管.

|
图 4 T1加权数据重建结果. (a) T1加权数据的全采图;(b)使用现有的CS-GRAPPA算法重建图;(c)使用本文方法重建图;(d)、(e)和(f)分别是(a)、(b)和(c)的细节放大图 Figure 4 Reconstruction for T1 weighted data. (a) T1 weighted full sampled image; (b) The reconstruction from 30% sampled k space by the existing CS-GRAPPA method; (c) The reconstruction using the proposed method from the same under-sampled k space; (d), (e) and (f) are details of (a), (b) and (c), respectively |
|
图 5 T2加权数据重建结果. (a) T2加权数据的全采图;(b)使用现有的CS-GRAPPA算法重建图;(c)使用本文方法重建图;(d)、(e)和(f)分别是(a)、(b)和(c)的细节放大图 Figure 5 Reconstruction for T2 weighted data. (a) T2 weighted full sampled image; (b) The reconstruction from 30% sampled k space by the existing CS-GRAPPA method; (c) The reconstruction using the proposed method from the same under-sampled k space; (d), (e) and (f) are details of (a), (b) and (c), respectively |
表 1展示了上述两组数据经CS-GRAPPA算法和我们所提出的方法的重建后得到的PSNR和SSIM值,可以看出我们所提出的方法在这两个参数上都优于现有的CS-GRAPPA算法.
| 表 1 使用现有CS-GRAPPA算法和本文方法重建T1加权数据和T2加权数据的结果评价 Table 1 PSNR and SSIM for the reconstructed T1 and T2 weighted images using the existing CS-GRAPPA and the proposed methods |
本文提出了一种新的结合GRAPPA和CS技术、进一步加速磁共振图像扫描速度的方法.在数据采样时,我们兼顾PI等间隔性和CS随机性的要求,设计了局部等间隔模板在k空间随机放的采样方式;在数据重建时,根据欠采行的重建模式,利用k空间中心全采ACS数据计算GRAPPA算法中相应的重建系数和重建误差,重建系数用于GRAPPA算法中欠采行的填充,重建误差用于后续的CS算法分权重保真中.实验结果证明:与现有方法相比,本文方法能减少随机伪影,提高图像PSNR,还原更多的图像细节.
| [1] | 周康荣, 陈祖望. 体部磁共振成像[M]. 上海: 上海医科大学出版社, 2000. |
| [2] |
GAO M, XIE H B, LI Z M, et al. A synchronized compressed sensing scan-reconstruction scheme in magnetic resonance imaging[J].
Chinese J Magn Reson, 2016, 33(2): 257-268.
高芒, 谢海滨, 李智敏, 等. 压缩感知同步扫描重建及其采样方案的研究[J]. 波谱学杂志, 2016, 33(2): 257-268. DOI: 10.11938/cjmr20160208. |
| [3] | 俎栋林, 高家红. 核磁共振成像[M]. 北京: 北京大学出版社, 2014. |
| [4] | PRUESSMANN K P, WEIGER M, SCHEIDEGGER M B, et al. SENSE:sensitivity encoding for fast MRI[J]. Magn Reson Med, 1999, 42(5): 952-962. DOI: 10.1002/(ISSN)1522-2594. |
| [5] | GRISWOLD M A, JAKOB P M, HEIDEMANN R M, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA)[J]. Magn Reson Med, 2002, 47(6): 1202-1210. DOI: 10.1002/(ISSN)1522-2594. |
| [6] | DONOHO D L. Compressed sensing[J]. IEEE T Inform Theory, 2006, 52(4): 1289-1306. DOI: 10.1109/TIT.2006.871582. |
| [7] | MAJUMDAR A, WARD R K. On the choice of compressed sensing priors and sparsifying transforms for MR image reconstruction:An experimental study[J]. Signal Process, 2012, 27(9): 1035-1048. |
| [8] | KUTYNIOK G. Theory and applications of compressed sensing[J]. Gamm-mitteilungen, 2012, 36(1): 79-101. |
| [9] | LUSTIG M, DONOHO D L, PAULY J M, et al. Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med, 2007, 58(6): 1182-1195. DOI: 10.1002/(ISSN)1522-2594. |
| [10] | LIU B, ZOU Y, YING L. Proceedings of the 5th international conference on information technology and application in biomedicine, in conjunction with the 2nd international symposium & summer school on biomedical and health engineering[C]. Shenzhen: IEEE, 2008. |
| [11] | ZHAO C, LANG T, JI J. Proceedings of the 16th international society of magnetic resonance in medicine[C]. Toronto: John Wiley & Sons, Inc, 2008. |
| [12] | LUSTIG M, PAULY J M. SPIRiT:Iterative self-consistent parallel imaging reconstruction from arbitrary k-space[J]. Magn Reson Med, 2010, 64(2): 457-471. |
| [13] | MURPHY M, ALLEY M, DEMMEK JAMES, et al. Fast L1-SPIRIT comprssed sensing parallel imaging MRI:scalable parallel implementation and clinically feasible runtime[J]. IEEE Trans Med Imaging, 2012, 31(6): 1250-1262. DOI: 10.1109/TMI.2012.2188039. |
| [14] | SHIN P J, LARSON P E, OHLIGER M A, et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion[J]. Magn Reson Med, 2014, 72(4): 959-970. DOI: 10.1002/mrm.24997. |
| [15] | LIANG D, LIU B, WANG J, et al. Accelerating SENSE using compressed sensing[J]. Magn Reson Med, 2009, 62(6): 1574-1584. DOI: 10.1002/mrm.v62:6. |
| [16] | KING K, XU D, BRAU A C, et al. Proceedings of the 18th international society of magnetic resonance in medicine[C]. Stockholm: John Wiley & Sons, Inc, 2010. |
| [17] | CHANG Y, LIANG D, YING L, et al. Nonlinear GRAPPA:A kernel approach to parallel MRI reconstruction[J]. Magn Reson Med, 2012, 68(3): 730-740. DOI: 10.1002/mrm.v68.3. |
| [18] | CHANG Y, KING K F, LIANG D, et al. IEEE 9th international symposium on biomedical imaging[C]. Barcelona: IEEE, 2012. |
| [19] | BEATTY P J, KING K F, MARINELLI L, et al. Proceedings of the 17th international society of magnetic resonance in medicine[C]. Honolulu: John Wiley & Sons, Inc, 2009. |
| [20] | WANG Z, WANG J, DETRE J A. Improved data reconstruction method for GRAPPA[J]. Magn Reson Med, 2005, 54(3): 738-742. DOI: 10.1002/(ISSN)1522-2594. |
| [21] | AJA-FERNÁNDEZ S, MARTÍN D G, TRISTÁN-VEGA A, et al. Improving GRAPPA reconstruction by frequency discrimination in the ACS lines[J]. Int J Comput Ass Rad, 2015, 10(10): 1699-1710. |
| [22] | YIN W, OSHER S, GOLDFARB D, et al. Bregman iterative algorithms for l1 minimization with applications to compressed sensing[J]. Siam J Imaging Sci, 2008, 1(1): 143-168. DOI: 10.1137/070703983. |
| [23] | WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment:from error visibility to structural similarity[J]. IEEE T Image Processing, 2004, 13(4): 600-612. DOI: 10.1109/TIP.2003.819861. |
 2018, Vol. 35
2018, Vol. 35 
