2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
铷原子频标(RAFS)具有体积小、功耗低、重量轻等优点,广泛应用于军用和民用领域,可实现导航定位、守时授时、时间同步等功能.近年来,随着信息网络的飞速发展,行业对时间频率的要求越来越高,铷频标得到了极大的发展和应用[1].
微波功率的稳定性是影响铷原子频标性能指标的重要因素.它体现在短期波动对稳定度的影响及长期变化对漂移的影响[2].
为了提高微波功率稳定性,通常做法是使功率放大器饱和输出,以此来稳定射频信号的幅度,从而稳定微波功率.但是这种情况下,功率放大器本身工作于饱和状态,输出波形失真严重,且温度变化会导致放大器静态工作点发生变化而进一步改变波形,所以虽然射频信号幅度不发生太大变化,但是波形变化较大,微波功率稳定性依旧不够理想.
本文通过对阶跃恢复二级管(SRD)的偏置电压控制实现微波功率的稳定,从而达到提高铷原子频标性能的目的.
1 电路设计在铷原子频率标准中,用于产生6.84 GHz微波信号的SRD一般工作于恒温环境,如果其输入信号(射频信号)幅度与波形均保持稳定状态,其倍频得到的微波信号功率也不发生变化.因此微波功率的稳定性取决于SRD输入的射频信号,在输入波形为正弦波的情况下,只要稳定射频信号功率(或幅度)就可以使微波功率处于稳定状态.
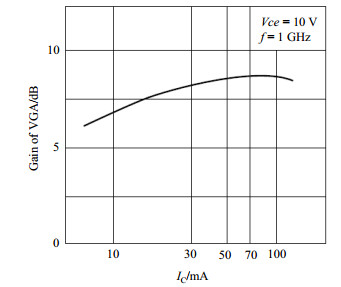
基于以上思路,本方案设计了一种微波功率稳幅电路,该电路主要包括可变增益放大器(VGA)、SRD和反馈电路(FB).选用的VGA增益与集电极电流(IC)的关系如图 1所示,IC在0~80 mA的范围内,当集电极射极电压(Vce)和待放大信号频率(f)恒定时,VGA增益随集电极电流的增大而增大.微波功率稳幅电路如图 2所示,89.93 MHz输入信号经过VGA放大之后输出给SRD进行76倍频得到6 834.68 MHz微波信号,SRD偏置电压反馈回FB,FB输出控制VGA基极电流,以此来调整VGA集电极电流和增益,进而实现自动增益控制(AGC),以此来稳定射频信号功率,最终达到改善微波功率稳定性的目的.
|
图 1 VGA增益与IC的关系 Figure 1 Gain of VGA vs. collector current (IC) |

|
图 2 微波功率稳幅系统组成 Figure 2 Composition of microwave power stabilization system |
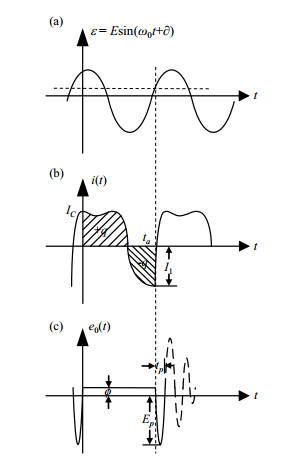
激励电压是正弦波的情况下,如图 3(a)所示,由于检波二极管少子的寿命很短(因常在制造过程中掺金作为载流子的复合中心,所以其寿命很短),电压正半周注入的少子很快被复合.当电压转向反向时,由于贮存的注入少子几乎已复合殆尽,故在反向电压作用下只可能有很小的反向电流,如图 3(b)所示.

|
图 3 检波管和阶跃管电流波形比较. (a)激励电压波形;(b)检波管电流波形;(c)阶跃管电流波形 Figure 3 Current waveform of detector diode and SRD. (a) Waveform of excitation; (b) Current waveform of detector diode; (c) Current waveform of SRD |
对于阶跃恢复二极管,其少子的寿命较长,不易被复合,由正向电流注入的少子分别贮存在PN结附近.当电压转为反向时,这些贮存电荷就被势垒电场拉回去,形成反向电流.直至反向激励的某个瞬间ta,如图 3(c),由正向期间储存下来的电荷被全部拉回去了,反向电流在此瞬间才突然陡降为0,出现了电流的阶跃[3].
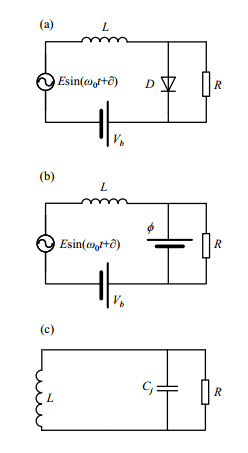
图 4(a)是阶跃管脉冲发生电路[4],其中L表示激励电感,D表示SRD,R表示负载电阻,Vb表示偏压电源;图 4(b)和4(c)分别表示在导通期间和阶跃期间的等效电路.考虑此时的信号源
| $ i(t)={{I}_{0}}+\frac{E}{{{\omega }_{0}}L}[\cos \partial-\cos ({{\omega }_{0}}t+\partial )]-\frac{{{V}_{b}}+\phi }{L}t $ | (1) |
|
图 4 阶跃管脉冲发生电路. (a)脉冲发生器电路;(b)导电区间等效电路;(c)阶跃区间等效电路 Figure 4 Pulse generation circuit of SRD. (a) Circuit of pluse generator; (b) Equivalent circuit of conductive section; (c) Equivalent circuit of step section |
|
图 5 正弦激励时,阶跃管的电流和电压波形. (a)激励电压;(b)电流波形;(c)电压波形 Figure 5 The current and voltage waveform of the SRD under sinusoidal excitation. (a) Excitation voltage; (b) Current waveform; (c) Voltage waveform |
(1) 式中I0表示初始电流,Vb表示偏置电压,由(1)式可知电流包括三个部分:直流分量,余弦分量和线性增长量,其波形如图 5(b)所示,对应的电压波形如图 5(c)所示.当阶跃管贮存的电荷释放完之后电流发生阶跃,阶跃管进入截止状态,此时其表现为一个小的反偏电容Cj,等效电路如图 4(c)所示,此时加在阶跃管两端的电压为0,也就是信号源与偏置电压在此瞬间抵消[5],即:
| $ {{V}_{b}}=E\sin ({{\omega }_{0}}t+\partial )=E\sin (\partial -\frac{\pi {{\omega }_{\text{0}}}}{{{\omega }_{N}}}) $ | (2) |
其中
| $ {{\omega }_{N}}=\frac{\sqrt{1-{{\xi }^{2}}}}{\sqrt{L{{C}_{j}}}} $ |
其中
| $ \xi =\frac{1}{2{{R}_{L}}}\sqrt{\frac{L}{{{C}_{j}}}} $ |
由(2)式可以看到偏置电压与输入信号幅度成正比,实际电路中偏置电压通过偏置电阻内建.
对于检波二极管,其检波电压与输入信号功率也就是幅度的平方成正比[6],虽然SRD偏置电压与输入信号的幅度成正比,但是检波电压或者偏置电压的稳定均代表着输入信号幅度的稳定,所以这里可以将阶跃管作检波管使用,稳定阶跃管的偏置电压就可以稳定输入射频信号的幅度.
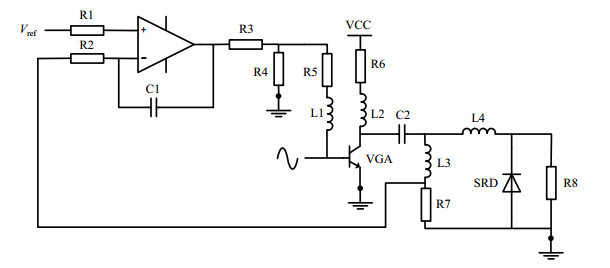
2.2 AGC工作原理AGC主要电路(部分配置电路忽略,如SRD匹配电路等)如图 6所示,输入信号经过VGA放大输出给SRD进行阶跃倍频,取SRD偏置电压Vb(电阻R7两端电压)反馈至运放反相输入端进行减法积分运算,积分输出反馈回VGA基极控制其基极电流,其中Vref由基准电压源提供.工作原原理如下:温度变化导致VGA增益和静态工作点变化,引起偏置电压Vb以及运放输出电压变化,导致VGA基极和集电极电流变化,由于VGA增益随集电极电流的增大而增大,所以VGA增益和静态工作点得到调整,从而实现自动增益控制.
|
图 6 AGC原理图 Figure 6 Schematic diagram of AGC |
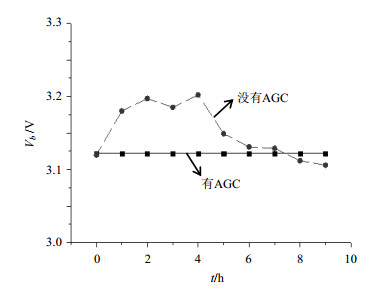
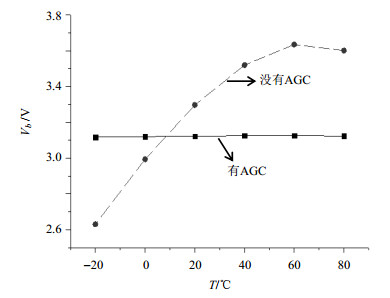
图 7是常温条件下连续测量得到的偏置电压Vb随时间t变化的曲线,图 8是变温条件下偏置电压Vb随温度T的变化曲线,其中虚线表示没有AGC时偏置电压Vb变化曲线,实线表示有AGC时偏置电压Vb变化曲线.从图中可以看出,这种电路方案能有效地稳定偏置电压.
|
图 7 常温下连续测量偏置电压曲线 Figure 7 Bias voltage curve of continuous measurement at room temperature |
|
图 8 偏置电压随温度变化曲线 Figure 8 Bias voltage varing with variable temperature |
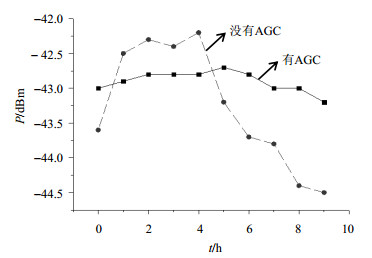
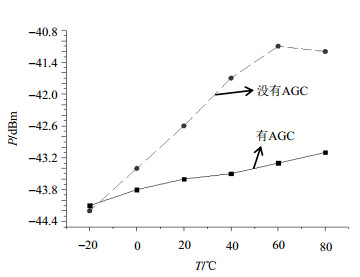
微波功率稳定性测量示意图如图 9所示,信号发生器(直接数字综合器)输出幅度为0 dBm的89.93 MHz信号[7],经过VGA放大约20 dB后进行阶跃倍频得到6 834.68 MHz微波信号,微波信号的测量主要是由频谱仪通过固定在谐振腔[8]上的耦合环耦合探测得到,测量结果如图 10和图 11所示.图 10是常温下连续测量情况下得到的微波功率随时间变化的曲线,图 11是变温条件下微波功率随温度变化的曲线.其中虚线表示没有AGC时微波功率变化曲线,实线表示有AGC时微波功率变化曲线.

|
图 9 微波功率稳定性测量示意图 Figure 9 Schematic diagram of microwave power stability measurement |
|
图 10 常温下连续测量微波功率曲线 Figure 10 Microwave power curve of continuous measurement at room temperature |
|
图 11 变温条件下微波功率曲线 Figure 11 Microwave power varing with variable temperature |
从图中可以看出,不论是常温下连续测量还是变温条件下测量,有AGC时的微波功率稳定性都要明显优于无AGC时微波功率稳定性.对比图 7和图 10中无AGC时偏置电压和微波功率随时间的变化曲线可以看出微波功率与偏置电压的变化曲线非常相似,间接说明通过稳定偏置电压来稳定微波功率的方案是可行的.
从图 11中可以观察到变温条件下有AGC时,微波功率稳定性更高,但依旧有较大的变化.可能原因有以下三种:(1)温度变化导致VGA工作点发生变化,进而导致VGA输出失真,输出射频信号波形发生变化;(2)SRD属于温度敏感器件,其工作环境温度发生了变化,即便很小的变化也可能导致其工作状态发生较大的改变;(3)温度变化导致Vref发生了变化,根据实际的测量数据,在变温条件下Vref确实发生了小幅变化.
将该电路接入铷频标闭环,测量得到微波功率频移系数即相对频率偏差
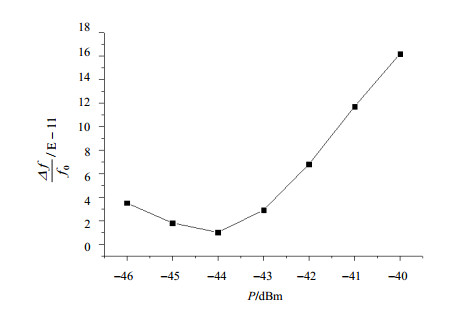
|
图 12 微波功率频移系数曲线 Figure 12 The curve of microwave power frequency shift coefficient |
根据图 11中的测量数据,-20 ℃至80 ℃范围内,无AGC和有AGC的情况下微波功率的变化量分别为3 dB和1 dB,那么得到的微波功率的变化量分别为0.03 dB/℃和0.01 dB/℃,由于此时微波功率频移系数为3E-11/dB,那么计算得到微波功率的变化引起的频率温度系数分别约为1E-12/℃和3E-13/℃.
4 结论及展望本文以阶跃恢复二极管的偏置电压为参考,通过控制可变增益放大器增益实现自动增益控制(AGC)的方案,能有效地提高微波功率稳定性.从图 11可以看到在-20 ℃~80 ℃变温条件下采用AGC方案与不采用AGC方案时微波功率变化幅度分别为1 dB和3 dB,也就是采用这种AGC控制方案使微波功率稳定性提升了3倍;从图 10可以看到在常温下连续测量条件下采用AGC方案与不采用AGC方案时微波功率变化幅度为0.5 dB和2.3 dB,微波功率稳定性提升了4倍;将该方案所设计的电路接入铷频标系统闭环测试发现整机温度系数有明显改善,经过计算得出因微波功率的变化引起的频率温度系数由1E-12/℃降低至3E-13/℃,这将有利于有效改善铷频标的长期稳定度指标和工作温度范围.
| [1] |
SHENG R W, GAO W, CHEN Z Y, et al. Development of small rubidium atomic frequency standar[C]. Academic Papers of Time and Frequency, 2009:129-131.
盛荣武, 高伟, 陈智勇, 等. 小型铷原子频标的发展[C]. 全国时间频率学术会议论文集. 2009: 129-131. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGTW200910002025.htm |
| [2] | 王义遒, 王庆吉, 傅济时, 等. 量子频标原理[M]. 北京: 科学出版社, 1986: 400-402. |
| [3] | 清华大学《微带电路》编写组. 微带电路[M]. 北京: 人民邮电出版社, 1976: 319-322. |
| [4] | 郑博仁. 0. 2——18G梳状谱信号发生器研究[D]. 成都: 电子科技大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10614-2005094882.htm |
| [5] | 宋伟. 毫米波检波器的研究与设计[D]. 成都: 电子科技大学, 2007. http://cdmd.cnki.com.cn/article/cdmd-10614-2007050815.htm |
| [6] | 吴宝东. 微波倍频技术的研究[D]. 南京: 南京理工大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10288-2007197455.htm |
| [7] |
LI Y W, XIAO L. Magnetic resonance imaging RF pulse generator basing on FPGA and DDS[J].
Chinese J Magn Reson, 2016, 33(4): 590-596.
李聿为, 肖亮. 基于FPGA与DDS的磁共振成像射频脉冲发生器[J]. 波谱学杂志, 2016, 33(4): 590-596. DOI: 10.11938/cjmr20160408. |
| [8] |
WANG P F, WANG C, HE S G, et al. A grooved microwave cavity for high precision miniaturized rubidium frequency standard[J].
Chinese J Magn Reson, 2016, 33(3): 452-457.
王鹏飞, 王晨, 何胜国, 等. 一种用于高精度小型化铷频标的开槽管微波腔[J]. 波谱学杂志, 2016, 33(3): 452-457. DOI: 10.11938/cjmr20160310. |
 2017, Vol. 34
2017, Vol. 34 
