2. Departments of Ophthalmology and Radiology, NYU Langone Medical Center, New York University School of Medicine, New York 10016, United States
2. Departments of Ophthalmology and Radiology, NYU Langone Medical Center, New York University School of Medicine, New York 10016, United States
磁共振眼球成像,已经广泛的应用于临床诊断中,例如用于葡萄膜黑色素瘤、视网膜母细胞瘤等眼部肿瘤的检测[1-4].无需介入即可呈现物质内部结构,同时不同于光学成像方法,无需清晰的光线通路,可观测肿瘤的大小、位置、及邻近组织解剖结构情况等优点,使得磁共振成像(Magnetic Resonance Imaging, MRI)成为眼球研究的有力工具[5-7].
然而,相比于光学成像方法,磁共振眼球成像也有它自身的一些缺点,例如分辨率较低、信噪比不足、容易产生运动伪影等.在MRI中,分辨率、信噪比和成像时间是3个相互制约的因素,它们不可能同时达到最优状态.对于眼球这个特殊的组织,它有较为精细的结构,需要较高的分辨率才可观察清楚.要想得到高分辨率和高信噪比的磁共振眼球图像,就需要较长的扫描时间.而人的眼球是一个易于活动的器官,很容易产生运动,较长的扫描时间会不可避免的使磁共振眼球图像产生运动伪影[8],降低图像质量.在闭上眼睛时,眼球会产生不由自主的全方位的运动,既有平面内的运动,又有跨越平面的运动.
为了解决磁共振眼球成像运动伪影的问题,一些学者提出了不同的策略,最常见的是“周期性眨眼的序列”[2, 9, 10].然而,这种方法需要受试者非常精确的配合.受试者在接受扫描时需要将眼睛目光汇聚在一个固定的位置,根据系统自动发出的提示音,每间隔一个短暂的时间眨眼一次,然后继续将目光盯住那个固定的位置.其中眨眼的瞬间机器是暂停扫描的.这种成像方法不经过训练很难一次成功.当受试者配合有偏差时,这种方法就会使图像质量明显下降.另外,近期还有学者在研究磁共振眼球成像方法时,让受试者睁开眼睛盯住一个位置,用探针检测眨眼,在不成像的眼睛涂上含有氧化铁的睫毛膏,当系统检测到受试者眨眼时,重新采集被破坏的K空间数据[11].这种方法抑制了眨眼伪影,但同样需要受试者的配合,同时还需要额外的硬件设备并将其集成到系统中,增加了成像的复杂性.
现阶段大多数磁共振运动伪影校正方法只对整体的刚性运动有效,对于类似眼球这种存在局部的全方位运动的特殊部位,有学者在解决运动伪影的问题时提出了一种“快速磁共振成像三维体重建”(Snapshot magnetic resonance imaging with Volume Reconstruction, SVR)的方法,并将其应用到孕妇体内的胎儿大脑MRI中[12].这种方法使用单层高速成像序列扫描以“冻结”胎儿大脑的运动.经过连续的移位采集以覆盖整个成像区域并确保足够的采样密度.使用6自由度刚性配准进行体积内的单层图像的回顾性对准.然后,应用基于B样条散射数据内插(B-spline Scattered Data Interpolation, SDI)的数据融合算法以生成最终的三维胎儿大脑图像.这种成像方法可以有效的抑制胎儿大脑的运动伪影,但对于眼球成像,其采集分辨率远高于胎儿大脑,以至于成像序列的单层采集时间无法足够短,进而难以“冻结”眼球的运动,部分图像会被运动破坏导致后续的配准不准确.尽管有磁共振并行成像方法可以加快扫描速度,但并行成像重建引起的信噪比损失会使一些图像信号淹没在噪声之中,同样使配准有时难以准确实现.这种方法并不适合眼球这一部位.
针对磁共振眼球成像中存在的这些问题,本文研究并实现了一种以超分辨率理论为基础的新的磁共振眼球成像方法.超分辨率,是一种利用一系列低分辨率图像生成一幅高分辨率图像的技术.在磁共振成像中,超分辨率更多的被应用于层厚方向分辨率的提升[13, 14].有的学者研究了平面内的磁共振超分辨率,对于静止的物体,通过平面内成像视野区域(Field Of View, FOV)的亚像素位移,实现平面内的图像分辨率的提升[15].这一方法刚一提出便受到了争议[16].由于平面内成像视野区域的亚像素位移对应于将采样后的K空间信号进行线性相位调制,不同的具有亚像素位移的成像视野区域所获取的磁共振图像的信号除了噪声之外并没有不同之处,不能提供用于平面内超分辨率的额外的信息.然而,另有学者指出,如果物体本身在多次扫描之间发生了运动,新的额外的信息会被引入[17-19],使平面内的超分辨率成为可能,但是其额外引入的信息量的大小未能被精确确定[19].
本文提出了一种新的磁共振平面内超分辨率的策略,实现了平面内的超分辨率重建,并将这一技术运用于磁共振眼球成像中.由于在磁共振成像过程中,平面内的频率编码方向和相位编码方向可以有不同的采集分辨率.在采集磁共振信号时,可以在同一成像视野区域内采集两组数据,它们的相位编码方向正交,每组数据的频率编码方向和相位编码方向具有不同的采集分辨率,使得这两组数据在不同的方向上分辨率互补.另外通过旋转成像视野区域使得各方向上的采集分辨率都得到互补,运用合适的超分辨率算法,可使平面内的分辨率得到提升.
为了验证本文算法的有效性,我们先做了仿体的测试实验,产生了较好的效果,之后又在人体上采集了眼球数据,根据本文提出的新的磁共振眼球成像方法,受试者在接受扫描时,闭上眼睛,不需要做额外的配合工作.对每一个受试者,采集6组数据,这6组数据共享完全相同的参数,只是成像视野区域相对于中心分别旋转了一定的角度.这6组数据可分为3对,其中每对的两组数据在相位编码方向正交,频率编码方向和相位编码方向上的采集分辨率互补.每组数据都含有若干动态图像.由于眼球的不自主运动是刚性的,对于这些动态的数据,可以对眼球的运动做平面内的配准,然后丢弃一部分配准系数较低的帧.配准是超分辨率的一个必要步骤,由于在磁共振眼球成像时,层内的眼球运动可以通过配准来描述.而当不同的动态图像之间发生层间的运动时,会在眼球的不同层面成像,导致配准系数降低.显然层间的运动会降低配准系数,因此丢弃一部分配准系数较低的图像可以适当的减少层间的运动伪影.此外,由于采集每一帧图像的动态时间不可能足够短,导致部分动态图像会在一定程度上被运动破坏,这些运动伪影较大的帧也会因为配准系数较低而被丢弃.之后,本文通过最大后验概率(Maximum a Posteriori Probability, MAP)超分辨率算法[20-22]提升层内的分辨率并且抑制了运动伪影.根据本文的采集策略,多组数据的分辨率可以互补,生成一个更高分辨率的图像.另一方面,眼球的不自主运动也可以提供超分辨率所需的亚像素位移.实验结果表明,本文方法在不需要受试者做额外配合、也不需要额外的磁场探针等硬件设备的情况下,可以得到更清晰的磁共振眼球图像,抑制了运动伪影的同时,提高了图像的分辨率,使图像的质量得到了提升.
1 理论基于超分辨率重建算法,是将一系列同一场景但有差异的低分辨率图像合成为一幅高分辨率图像.1984年,Tsai和Huang[23]开创了由低分辨率图像序列复原单幅高分辨率图像的工作,给出了频域的复原方法.该方法计算简单,但模型中没有考虑光学系统点扩散函数(Point Spread Function, PSF)、运动模型和观测噪声等因素的影响,且只能处理图像整体的运动,对于眼球这种局部运动无能为力.空域法是当前的主流方法之一,将复杂的全局和局部运动、光学模糊、空间可变PSF,以及非理想采样并入其中,并且具有很强的包含空域先验约束的能力.
对于空域法,可以设定一个由高分辨率到低分辨率的图像观测模型,即假设采集到的图像是由高分辨率图像变换得到[24].这些变换包括几何平移、旋转、图像PSF模糊、降采样等操作.现假设高分辨率图像为X,低分辨率图像为yk,k,1,2,3,….对于每幅低分辨率图像yk,k,1,2,3,…,可视为由高分辨率图像X,经过刚性几何变换Gk,PSF模糊Bk,降采样Dk,再加上噪声Vk而得到,即
| $ {{y}_{k}}={{D}_{k}}{{B}_{k}}{{G}_{k}}X+{{V}_{k}}, k=1, 2, 3, \cdots $ | (1) |
令
| $ {{y}_{k}}={{D}_{k}}{{B}_{k}}{{G}_{k}}X+{{V}_{k}}={{W}_{k}}X+{{V}_{k}}, k=1, 2, 3, \cdots $ | (2) |
根据这一模型,超分辨率重建就转换为求解X的数学问题,这是一个不适定问题,有许多求解方法.本文采用了MAP法[20-22]求解.MAP法是空域法中统计方法的典型代表,它把超分辨率问题看成一个统计估计问题,在已知一系列低分辨率图像序列的前提下,使出现高分辨率图像的后验概率达到最大,再利用贝叶斯公式,得
| $ {{X}_{MAP}}=\underset{X}{\mathop{\arg \max }}\, P(X|{{y}_{1}}, {{y}_{2}}, {{y}_{3}}, \cdots )=\underset{X}{\mathop{\arg \max }}\, P(X|Y)=\underset{X}{\mathop{\arg \max }}\, \frac{P(Y|X)P(X)}{P(Y)} $ | (3) |
将(3)式中目标函数取对数,不改变其极值点,得:
| $ {{X}_{MAP}}=\underset{X}{\mathop{\arg \max }}\, [\ln P(Y|X)+\ln P(X)-\ln P(Y)]=\underset{X}{\mathop{\arg \max }}\, [\ln P(Y|X)+\ln P(X)] $ | (4) |
假设图像噪声具有多变量高斯分布,所有低分辨率图像之间的噪声变量是相互独立的,于是
| $ P({{V}_{k}})=P({{y}_{k}}-{{W}_{k}}X) $ | (5) |
根据Gauss随机场模型,在给定原始图像条件下,由于随机噪声的影响,采集观测到的图像数据yk可视为一个随机场.可以认为该随机场的均值是WkX.按照标准多变量高斯模型,给定X条件下yk的分布应该符合下式:
| $ P({{y}_{k}}|X)=P({{y}_{k}}-{{W}_{k}}X)=P({{V}_{k}}) $ | (6) |
因此
| $ P({{y}_{k}}|X)=\frac{1}{\sqrt{{{(2\pi )}^{L}}\det |{{Q}_{\eta }}|}}\exp \left[-\frac{1}{2}{{({{y}_{k}}-{{W}_{k}}X)}^{T}}Q_{\eta }^{-1}({{y}_{k}}-{{W}_{k}}X) \right] $ | (7) |
其中L是图像yk的大小(像素点个数);
(4) 式中P(X)可视为高分辨率图像X的先验约束项,不同类型的图像先验知识可以被用作估计P(X).Schultz和Stevenson基于统计估计框架,提出的一种具有边缘保持能力的Huber-Markov模型在MAP超分辨率算法中得到了广泛的应用[21],其数学表达式为:
| $ P(X)=\frac{1}{Z}\exp \left\{ -\frac{1}{2\beta }\sum\limits_{c\in C}{\rho }[d_{c}^{t}(X), \alpha] \right\} $ | (8) |
在(8)式中,Z为归一化常数;β为Gibbs先验温度参数;c是一个局部像素组,称为团块,而图像上所有的团块构成集合C;
| $ d_{m, n, 1}^{t}(X)={{X}_{m, n-1}}-2{{X}_{m, n}}+{{X}_{m, n+1}} $ | (9) |
| $ d_{m, n, 2}^{t}(X)=0.5{{X}_{m+1, n-1}}-{{X}_{m, n}}+0.5{{X}_{m-1, n+1}} $ | (10) |
| $ d_{m, n, 3}^{t}(X)={{X}_{m-1, n}}-2{{X}_{m, n}}+{{X}_{m+1, n}} $ | (11) |
| $ d_{m, n, 4}^{t}(X)=0.5{{X}_{m-1, n-1}}-{{X}_{m, n}}+0.5{{X}_{m+1, n+1}} $ | (12) |
其中,
图像数据边缘像素点的概率被Huber边缘惩罚函数[21, 25]所控制,其定义为:
| $ \rho (x, \alpha ) = \left\{ \begin{array}{l} {x^2}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |x|\alpha \\ 2\alpha |x| - {\alpha ^2}, \ \ |x| > \alpha \end{array} \right. $ | (13) |
(13)式中,α为阈值参数,控制先验模型的不连续性大小.将(7)~(13)式、代入(4)式中,得到高分辨率图像的最大后验概率估计为:
| $ {X_{MAP}} = \mathop {\arg \min }\limits_X \left\{ {\sum\limits_{k = 1}^N {||{y_k} - {W_K}X||_2^2} + \gamma \sum\limits_{(m, n)} {\sum\limits_{r = 1}^4 \rho } [d_{m, n, r}^t(X), \alpha]} \right\} $ | (14) |
其中γ是P(X)先验知识项的权重系数.
2 材料与方法实验包括仿体实验及在体实验两部分,仿体成像实验对象为圆柱水模,在体成像实验部位为志愿者眼部区域,感兴趣区域(Region Of Interest, ROI)为眼球.所有的扫描实验均在Philips 3.0 T Achieva TX MRI设备(Philips Healthcare, Best, The Netherlands)上完成.
2.1 仿体实验对圆柱水模,我们在横断面先后采集了6组数据,其中前两组的成像视野区域绕着FH轴相对区域中心旋转了0°,中间两组旋转-30°,最后两组旋转30°.在每对数据中,相位编码方向相互正交,相位编码方向的分辨率设置为1 mm,而频率编码方向的分辨率为4 mm,层厚为4 mm.采用2D T1FFE序列,采集一层图像,成像视野区域为256×256 mm2,翻转角(Flip Angle, FA)为5°,脉冲间隔重复时间/回波时间(Repetition Time/Echo Time, TR/TE)= 2.5 ms/2.1 ms,半傅里叶采集K空间52.5%的数据.
对于PSF,本文选用高斯函数,使其半高宽等于图像像素点的单位大小.P(X)先验知识项的权重系数γ设置为0.002.在求解XMAP时,使用梯度下降法迭代求解.
| $ {X_{n + 1}} = {X_n} + \left\{ {\sum\limits_{k = 1}^N {W_k^T({y_k} - {W_K}{X_n}) + } \gamma \sum\limits_{(m, n)} {\sum\limits_{r = 1}^4 {{{(d_{m, n, r}^t)}^T}\rho '[d_{m, n, r}^t({X_n})} }, \alpha]} \right\} $ | (15) |
其中
| $ \rho '(x, \alpha ) = \left\{ \begin{array}{l} 2x, \ \ \ \ \ \ \ \ \ \ \ \ \ \ |x|\geqslant\alpha \\ 2{\rm{sign}}(x)\alpha, \ \ |x| > \alpha \end{array} \right. $ | (16) |
需要注意的是,所有的图像在计算时都需要按照先列后行的顺序拉成一个向量,因而变换矩阵Wk是一个大型稀疏矩阵,它作用于图像向量时,相当于对图像做某种线性变换,最终求得的XMAP也是一个向量,还需重新变形成对应大小的图像矩阵.
2.2 在体实验 2.2.1 准备工作为了得到更高质量的磁共振眼球图像,我们定制了一个特殊的线圈,如图 1所示.该线圈为4通道眼球线圈,每个眼球各有两个通道.在扫描前,我们先将受试者成像的眼部盖上一层湿的纱布以减小与空气交界处的场不均匀性伪影[2, 26, 27].带上眼球线圈之后,我们用绑带将线圈绑在面部上方,增加稳定性,使其更加贴近眼部,增加图像的信噪比,如图 2所示.

|
图 1 4通道眼球线圈 Figure 1 The four-channel orbit coil |

|
图 2 将眼球线圈用绑带固定,使其贴近眼部,增加图像信噪比 Figure 2 The orbit coil is fixed with a strap to keep it closer to the eye and to increase the signal to noise ratio of the images |
对于眼球,和水模数据的采集一样,我们在横断面先后采集了6组数据,同样对成像视野区域绕着FH轴方向相对区域中心进行了旋转操作.在每对数据中,相位编码方向相互正交.为了保持每一帧动态的图像具有一定的信噪比,相位编码方向的分辨率设置为0.2 mm,而频率编码方向的分辨率为0.6 mm,层厚为3 mm.所有的数据采集都使用2D T1FFE序列,仅采集一层,成像视野区域为192×192 mm2,翻转角为7°,TR/TE = 8.5 ms/4.1 ms,半傅里叶采集K空间52.5%的数据以加快动态采集时间.每组数据含有20帧,每一帧的动态时间为4.3 s,总共的采集时间为8 min 36 s.频率编码方向上较低的分辨率可以增加动态图像的信噪比,而动态扫描可以很大程度上抑制运动伪影.每一帧的动态时间需要尽可能的短,以“冻结”眼球的运动,部分未被“冻结”的眼球图像会在随后的处理中被丢弃.受试者在接受扫描时只需将眼睛闭上,不需要做任何睁眼眨眼等配合的工作.由于扫描是动态的,我们可以观察到眼球的不自主运动.
2.2.3 预处理工作由于在数据采集时,平面内的分辨率较高,采集时间较短,导致图像有较低的信噪比.此外,由于眼球不自主运动的存在(包括平面内的运动和穿越平面的运动),部分图像帧被严重的破坏,这些帧的信号强度明显异常.在数据预处理部分,我们将剔除掉这部分信号强度异常的帧.剔除的比例为10%,对于每组20帧的动态扫描,保留其中的18帧数据.
在剔除信号异常的数据时,对于每组数据,我们先计算出每一帧的图像的信号强度,将所有帧的信号强度按顺序保存为一个向量
然后,我们对噪声的方差进行估计.假设图像噪声部分的实部和虚部符合独立的、有着相同的方差的高斯分布,那么其幅值符合瑞利分布,设方差为σ2.根据数学理论可知,由两个独立的、均值相同的、方差为σ2的瑞利分布的差产生的随机变量,其均值为0、方差为2σ2.对于每一组数据,若干动态图之间的噪声的幅值是相互独立的.在成像条件相同的条件下,其瑞利分布的均值和方差均大体一致.我们利用帧差法的思想,将每组数据若干帧动态的图像两两相减,试图通过相减去除掉图像本身的信号,而只留下背景噪声部分.两两相减后共得到若干幅帧差图,计算所有的帧差图的方差,找到其中最小的那一个,其对应的方差即近似为原始图像的噪声方差的2倍.因为方差最小的帧差图,已经通过相减几乎完全消除了图像信号本身的作用,而只保留了噪声部分.而方差较大的帧差图,则由于眼球运动的原因,遗留下了部分图像本身信号的作用,导致帧差图方差较大.
根据之前估计的图像噪声的方差σ2,我们使用BM3D算法[28]对每一幅动态图进行不同噪声方差估计下的去噪(协同滤波时选择合适的阈值).由于去噪会在一定程度上影响图像边缘部分的高频信息,我们将保留所有的方差估计下的去噪结果,在之后选择适当的去噪图像进行后续的计算.
2.2.4 图像配准如果眼球的运动只发生在平面内,那么由于眼球的球体部分的运动是刚性的,所以可以用刚性的配准描述眼球在平面内的运动情况.然而,穿越平面的运动也时常存在,导致图像前后采集的不一致性.另一方面,由于图像分辨率较高,导致动态采集的周期不能足够短,在采集某一帧数据时,眼球的运动仍可以破坏在这一帧数据,使其产生运动伪影.鉴于上述情况,我们将根据配准的结果丢弃一部分数据,以减少层内和穿越层厚方向的运动伪影.
图像配准是超分辨率算法中关键的一步,其配准的精度对最终结果有至关重要的影响,必须要达到亚像素级别.在这一步中,对于每一组数据,我们都需要先选取一个参考帧.参考帧的眼球应是几乎没有运动伪影且恰好在所成像的平面内,几乎没有发生穿越平面的运动.由于眼球的不自主运动像是一种围绕某个中心的运动,对所有的动态图像做平均所得到的眼球图像可以作为匹配模板的近似估计.我们以图像矩阵的相关系数为标准,选取与平均图像相似度最大的帧作为配准的参考图像,将其他所有的图像与参考图像做配准.对于二维平面的刚体配准,有两个方向的平移量和旋转角度共3个自由度.
为了提高配准的精度和速度,我们选择了两种配准相似度度量标准,分别是相关系数和绝对差.这两种标准各有优劣,我们试图参考两者综合的结果作为配准的最终结果,以弥补单一标准下的不稳定性.此外,我们将图像进行双线性插值放大,以提高亚像素级别的配准精度.另一方面,我们将智能计算中的粒子群算法[29, 30]应用到配准过程中,以加快其计算速度及准确性.由于配准问题的规模和复杂度并不非常大,考虑到计算时间的问题,种群粒子数和迭代次数都不必过大,本文把两者都设置为35.对于3个自由度的刚性配准(旋转角度和x、y方向的位移),粒子的长度设置为3.考虑到眼球的运动在一定的范围内,粒子的范围设定也需要恰当,本文设置为
考虑到对眼球做二维的刚体变换时,ROI会发生改变,用模板图像去配准待配准图像时,待配准图像的ROI会对相似性度量标准产生影响.因此,我们需要在正式配准前先固定待配准图像的ROI,然后再做亚像素配准.具体的配准步骤如下.
1.选取好参考图像,选用噪声方差估计为0.8σ2的去噪结果,将眼球球体部分非常仔细地手动画入ROI,并计算ROI的几何中心的坐标.其中画ROI时需要将图像放大32倍以上,以保证其准确性.
2.对每一帧待配准图像,选用噪声方差估计为0.8σ2的去噪结果,利用粒子群算法寻找使相关系数达到最大的配准参数以及对应的待配准图像的ROI.此时的配准参数结果并不十分准确,只是用于计算待配准图像的ROI.
3.对每一帧待配准图像,选用噪声方差估计为0.8σ2的去噪结果,固定之前计算得到的待配准图像的ROI,利用粒子群算法寻找使相关系数达到最大的配准参数.
4.对每一帧待配准图像,选用噪声方差估计为0的去噪结果(即没有去噪),固定之前计算得到的待配准图像的ROI,利用粒子群算法寻找使绝对差达到最小的配准参数.
5.将第3步和第4步计算得到的配准参数取平均值.
之前提到,由于运动伪影的存在,并不是所有的眼球图像都有较好的质量.在配准工作结束之后,我们需要继续丢弃一部分数据.对于每一组数据,我们将每一帧眼球图像的配准相关系数按降序排序,将配准绝对差按升序排序.根据两个排序结果,可以将每一帧图像确定一个平均排名,显然排在第一位的应当是参考模板图(参考图的配准相关系数为1,绝对差为0).最后我们丢弃那些平均排名较低的图,可以在一定程度上抑制运动伪影.这里,我们将之前保留的每组的18帧数据剔除其中排名最靠后的5帧,最终每组数据留下13帧图像.
2.2.5 超分辨率对于平面内的PSF,我们选用高斯函数,使PSF的半高宽等于高分辨率像素点的单位大小.根据之前计算得到的配准结果和对PSF的估计,我们已经获知了每一幅图像的几何变形参数Gk和PSF模糊Bk,Dk也是已知的.P(X)先验知识项的权重系数γ=0.01.对于XMAP的求解,使用与仿体实验相同的方法.
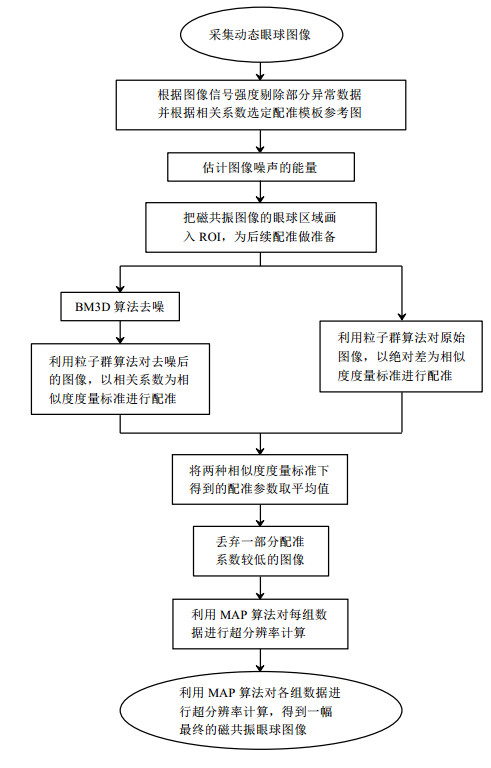
另外需要说明的是,对每组数据分别做完配准和超分辨率之后,得到了6幅不同方向上分辨率互补的图像,这6幅图像还需要继续用同样的方法做配准和超分辨率,生成一幅最终的磁共振眼球图像.本文方法的流程图如图 3所示.
|
图 3 图像获取与处理方法的流程图 Figure 3 The flow chart of image acquisition and processing |
在人体眼球实验之前,我们在仿体上作了超分辨率的测试.依照之前所叙述的采集策略,我们获得了若干幅低分辨率图像,并直接采集了高分辨率的图像作为参考图,如图 4所示.

|
图 4 仿体的超分辨率结果.(a)~(f)分别是6组不同方向上的低分辨率图像:(a)和(b)的成像视野区域绕着FH轴旋转了0°;(c)和(d)旋转-30°;(e)和(f)旋转30°;(a)与(b)、(c)与(d)、(e)与(f)的相位编码方向相互正交.相位编码方向的分辨率为1 mm,频率编码方向的分辨率为4 mm;(g)通过超分辨率算法得到的图像;(h)直接采集获取的高分辨率图像 Figure 4 Results of super-resolution reconstruction in a phantom. (a)~(f) are six low-resolution images in different directions: (a) and (b) are rotated by 0° around the FH axis; (c) and (d) are rotated by -30°; (e) and (f) are rotated by 30°. The phase encoding direction of (a) and (b), (c) and (d), (e) and (f) are orthogonal to each other. The resolution of the phase encoding direction is 1 mm, and the resolution in the frequency encoding direction is 4 mm. (g) The image obtained by the super-resolution algorithm; (h) The high-resolution image obtained by direct acquisition |
仿体实验结果表明,我们提出的采集策略配合MAP超分辨率算法确实可以提高图像分辨率,成功的实现了磁共振平面内的超分辨率.
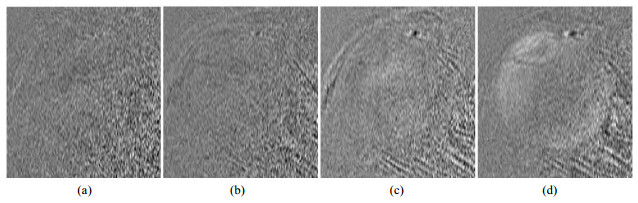
3.2 在体实验 3.2.1 噪声能量的估计及去噪的结果我们用帧差法将每一组若干动态图像两两相减后,得到了若干帧差图像,然后对这些图像的方差由小到大升序排序.图 5的(a)、(b)、(c)、(d)分别显示了某组数据中排序为1、60、120、180的帧差图,其方差依次为225.12、249.14、282.37、336.96.可以看出,方差小的帧差图(a),其图像信号被最大程度的消除掉,背景噪声得到了保留.由于眼球不自主运动的存在,部分图像相减后信号未被消除,导致方差较大.我们计算图 5(a)的方差就可以近似估计出图像背景噪声的能量.
|
图 5 在体数据帧差图.(a)~(d)帧差图的方差依次增大 Figure 5 Differences between two dynamic image frames during in vivo eyeball imaging. (a)~(d) represent increasing order of differences |
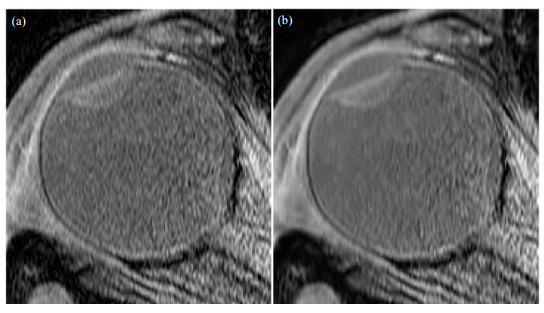
在得到了噪声的能量(方差)大小之后,我们使用BM3D算法[28]对图像进行去噪.某一帧图像去噪的结果如图 6所示.这里去噪只是为配准做准备,提高配准的相关系数及准确性,而不是用去噪后的图像做超分辨率.
|
图 6 在体数据某一帧图像的去噪结果.(a)原始图像;(b)噪声方差估计为0.8σ2的去噪结果 Figure 6 Results after denoising of an image frame. (a) The original image; (b) The denoising result with a noise variance estimated at 0.8σ2 |
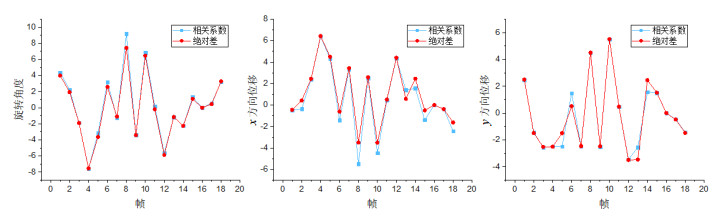
我们任意地选取了一组数据,将两种不同的相似度度量下的配准参数绘制成曲线图(图 7).可以看出,相关系数和绝对差用作相似度度量时,其配准结果比较吻合,但依然有误差.我们将两组配准参数取平均值,以降低单一标准下的误差.
|
图 7 在体数据配准结果.横坐标为帧,纵坐标分别是旋转角度和x、y方向的位移,蓝色线和红色线分别表示相关系数和绝对差度量下的配准结果 Figure 7 Results of data registration of in vivo images. x-axis represents the frame number, and y-axis represents the rotation angle (left), and the displacements in x-(middle) and y-directions (right). The blue and red lines represent the correlation coefficient and the absolute difference of the registration results, respectively |
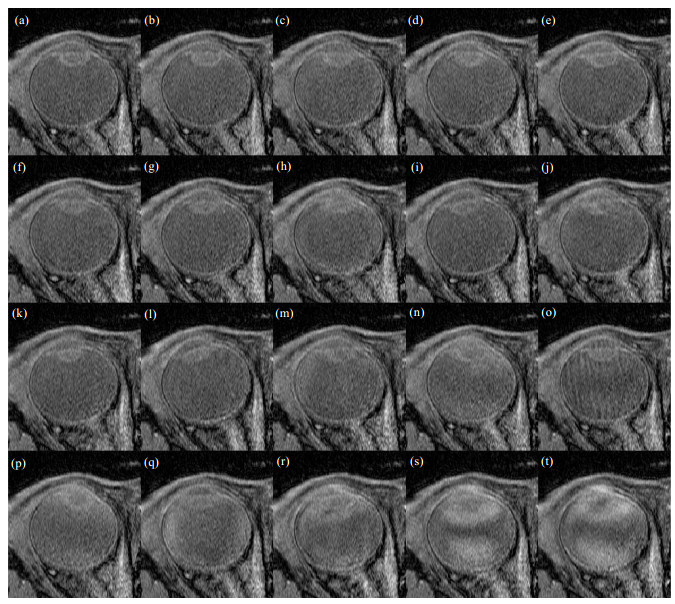
根据本文的方法,对每一组数据,最先根据信号强度丢弃20幅动态图像中的2幅,然后根据配准结果,再丢弃配准系数排名较靠后的5幅,最后剩下13幅图像用于超分辨率.我们任意选取一组数据,将20帧图像根据配准排序结果展示如下(图 8),其中最后2幅图像是根据信号强度丢弃的.
|
图 8 某一组数据的排序结果.(a)~(t)依次是配准系数排序由高到低的眼球图像 Figure 8 Image sorting based on registration coefficient. (a)~(t) represent the eyeball images in the order of decreasing registration coefficients |
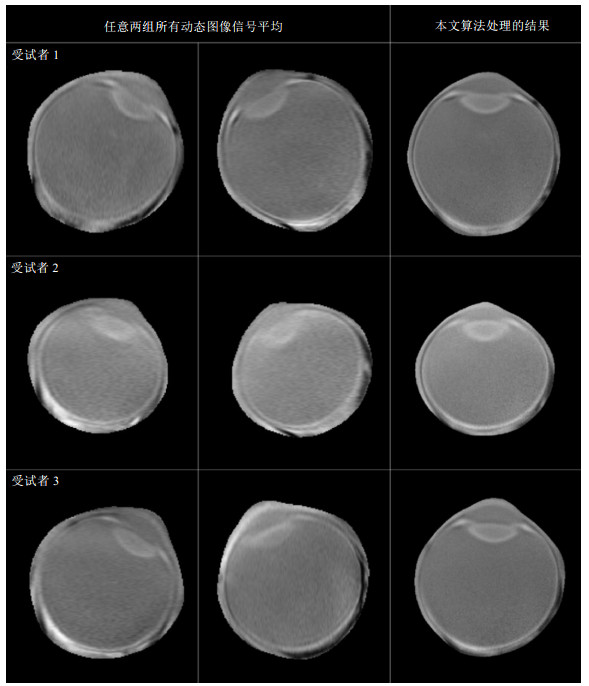
由图 9的结果可以看出,本文的算法可以使采集到的磁共振眼球图像质量得到提升,抑制了运动伪影的同时,提高了图像分辨率.特别是眼球边缘处,本文的方法可以更清晰的观察到眼球最外层的膜结构.
|
图 9 本文算法最终结果.前两列是每个受试者的任意两组所有动态图像信号平均的结果,第三列是本文算法处理的结果 Figure 9 The final results of the proposed algorithm. The first two columns represent the signal average of all dynamic images of two separate, arbitrary sets of data for each subject. The third column represents the results of the proposed algorithm |
本文从眼球成像的实际问题出发,为解决磁共振眼球成像中信噪比、分辨率和运动伪影三者之间的矛盾,提出了一种新的眼球图像获取方法.首先在成像时将受试者眼部盖上湿的纱布以抑制场不均匀性伪影.使用一种特制的眼球线圈,采集多组分辨率在不同方向上互补的动态眼球图像,再通过预处理,配准,异常数据丢弃,超分辨率等步骤,使磁共振眼球图像质量得到了提升.在整个图像数据采集过程中,受试者不需要做任何睁眼眨眼等配合工作,也不需要额外的磁场探针等硬件辅助,降低了成像的难度,减少了受试者的不舒适性.
需要说明的是,本文的方法只是为磁共振眼球成像提供了一种新的思路,其中的成像参数与数据处理中的参数并不是绝对的.在实际应用时,可以通过增加采集时间换取更高分辨率更高信噪比的眼球图像.异常数据丢弃的比例也是可以调整的,当丢弃数据过少时,会导致运动伪影的增加,丢弃数据过多时,会导致信噪比不足.此外,超分辨率算法中的先验知识权重系数也应选取为恰当适中的值.
最后要指出本文的算法所展现的效果来自3个方面共同作用的结果:一是运动伪影的消除;二是眼球不自主运动为磁共振平面内超分辨率提供的额外信息;三是不同方向互补的分辨率所带来的效果.这三个方面都为磁共振眼球图像质量的提升做出了贡献.
4 结论本文提出了一种新的眼球图像获取方法,在受试者不需要做任何配合工作的情况下,使磁共振眼球图像的运动伪影减少,分辨率提高,图像质量得到了提升.这一新的思路为临床上眼球疾病的诊断提供了新的方法,具有一定的实用价值.
| [1] | GRAAF P D, GÖRICKE S, RODJAN F, et al. Guidelines for imaging retinoblastoma:imaging principles and MRI standardization[J]. Pediatr Radiol, 2012, 42(1): 2-14. DOI: 10.1007/s00247-011-2201-5. |
| [2] | BEENAKKER J W, VAN RIJN G A, LUYTEN G P, et al. High-resolution MRI of uveal melanoma using a microcoil phased array at 7 T[J]. NMR Biomed, 2013, 26(12): 1864-1869. DOI: 10.1002/nbm.v26.12. |
| [3] | GRAESSL A, MUHLE M, SCHWERTER M, et al. Ophthalmic magnetic resonance imaging at 7 T using a 6-channel transceiver radiofrequency coil array in healthy subjects and patients with intraocular masses[J]. Invest Radiol, 2014, 49(5): 260-270. DOI: 10.1097/RLI.0000000000000049. |
| [4] | BEENAKKER J W M, FERREIRA T A, SOEMARWOTO K P, et al. Clinical evaluation of ultra-high-field MRI for three-dimensional visualisation of tumour size in uveal melanoma patients, with direct relevance to treatment planning[J]. MAGMA, 2016, 29(3): 571-577. DOI: 10.1007/s10334-016-0529-4. |
| [5] | HO L C, SIGAL I A, JAN N J, et al. Non-invasive MRI assessments of tissue microstructures and macromolecules in the eye upon biomechanical or biochemical modulation[J]. Sci Rep, 2016, 6: 32080. DOI: 10.1038/srep32080. |
| [6] | HO L C, SIGAL I A, JAN N J, et al. Magic angle-enhanced MRI of fibrous microstructures in sclera and cornea with and without intraocular pressure loading[J]. Invest Ophthalmol Vis Sci, 2014, 55(9): 5662-5672. DOI: 10.1167/iovs.14-14561. |
| [7] | HO L C, CONNER I P, DO C W, et al. In vivo assessment of aqueous humor dynamics upon chronic ocular hypertension and hypotensive drug treatment using gadolinium-enhanced MRI[J]. Invest Ophthalmol Vis Sci, 2014, 55(6): 3747-3757. DOI: 10.1167/iovs.14-14263. |
| [8] | LEMKE A J, ALAI-OMID M, HENGST S A, et al. Eye imaging with a 3.0-T MRI using a surface coil——a study on volunteers and initial patients with uveal melanoma[J]. Eur Radiol, 2006, 16(5): 1084-1089. DOI: 10.1007/s00330-005-0087-z. |
| [9] | BERKOWITZ B, MCDONALD C, ITO Y, et al. Measuring the human retinal oxygenation response to a hyperoxic challenge using MRI:Eliminating blinking artifacts and demonstrating proof of concept[J]. Magn Reson Med, 2001, 46(2): 412-416. DOI: 10.1002/(ISSN)1522-2594. |
| [10] | ZHANG Y, NATERAS O S E, PENG Q, et al. Lamina-specific anatomic magnetic resonance imaging of the human retina[J]. Invest Ophthalmol Vis Sci, 2011, 52(10): 7232-7237. DOI: 10.1167/iovs.11-7623. |
| [11] | WEZEL J, GARPEBRING A, WEBB A G, et al. Automated eye blink detection and correction method for clinical MR eye imaging[J]. Magn Reson Med, 2017, 78(1): 165-171. DOI: 10.1002/mrm.v78.1. |
| [12] | JIANG S, XUE H, GLOVER A, et al. MRI of moving subjects using multislice snapshot images with volume reconstruction (SVR):Application to fetal, neonatal, and adult brain studies[J]. IEEE Trans Med Imaging, 2007, 26(7): 967-980. DOI: 10.1109/TMI.2007.895456. |
| [13] | GREENSPAN H, PELED S, OZ G, et al. MRI inter-slice reconstruction using super-resolution[C]//International conference on medical image computing and computer-assisted intervention. Berlin Heidelberg:Springer-Verlag, 2001:1204-1206. |
| [14] | GREENSPAN H, OZ G, KIRYATI N, et al. MRI inter-slice reconstruction using super-resolution[J]. Magn Reson Imaging, 2002, 20(5): 437-446. DOI: 10.1016/S0730-725X(02)00511-8. |
| [15] | SHARON P, YEHEZKEL Y. Superresolution in MRI:Application to human white matter fiber tract visualization by diffusion tensor imaging[J]. Magn Reson Med, 2001, 45(1): 29-35. DOI: 10.1002/(ISSN)1522-2594. |
| [16] | SCHEFFLER K. Superresolution in MRI?[J]. Magn Reson Med, 2002, 48(2): 408-409. DOI: 10.1002/(ISSN)1522-2594. |
| [17] | CARMI E, LIU S Y, ALON N, et al. Resolution enhancement in MRI[J]. Magn Reson Imaging, 2006, 24(2): 133-154. DOI: 10.1016/j.mri.2005.09.011. |
| [18] | MITCHELL R J, MAYER G S, LAUZON L M, et al. Synthetic aperture MRI:US, US7005854[P]. 2006. |
| [19] | MAYER G S, VRSCAY E R. Mathematical analysis of "phase ramping" for super-resolution magnetic resonance imaging[M]//CAMPILHO A, KAMEL M S. Image Analysis and Recognition. Berlin Heidelberg:Springer, 2006:82-93. |
| [20] | SCHULTZ R R, STEVENSON R L. Improved definition image expansion[C]. In ICASSP, IEEE international conference on a coustics, speech and signal processing-proceedings. 1992, 3:173-176. |
| [21] | SCHULTZ R R, STEVENSON R L. A Bayesian approach to image expansion for improved definition[J]. IEEE T Image Process, 1994, 3(3): 233-242. DOI: 10.1109/83.287017. |
| [22] | SCHULTZ R R, STEVENSON R L. Extraction of high-resolution frames from video sequences[J]. IEEE T Image Process, 1996, 5(6): 996-1011. DOI: 10.1109/83.503915. |
| [23] | TSAI R Y, HUANG T S. Multiframe image restoration and registration[C]//Advances in computer vision and image processing. 1984. |
| [24] | IRANI M, PELEG S. Improving resolution by image registration[J]. Cvgip Graphical Models & Image Processing, 1991, 53(3): 231-239. |
| [25] | STEVENSON R L, SCHMITZ B E, DELP E J. Discontinuity preserving regularization of inverse visual problems[J]. IEEE T Sys Man Cy, 1994, 24(3): 455-469. DOI: 10.1109/21.278994. |
| [26] | BERT R J, PATZ S, OSSIANI M, et al. High-resolution MR imaging of the human eye 20051[J]. Acad Radiol, 2006, 13(3): 368-378. DOI: 10.1016/j.acra.2005.10.023. |
| [27] | RICHDALE K, WASSENAAR P, TEAL B K, et al. 7 Tesla MR imaging of the human eye in vivo.[J]. J Magn Reson Imaging, 2009, 30(5): 924-932. DOI: 10.1002/jmri.v30:5. |
| [28] | DABOV K, FOI A, KATKOVNIK V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE T Image Process, 2007, 16(8): 2080-2095. DOI: 10.1109/TIP.2007.901238. |
| [29] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks, 1995, 4:1942-1948. |
| [30] | EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]//International Symposium on MICRO Machine and Human Science. IEEE, 1995:39-43. |
 2017, Vol. 34
2017, Vol. 34 
