2. 中国石油大学(北京) 理学院, 北京 102249;
3. Harvard SEAS-CUPB Joint Lab. on Petroleum Science, Cambridge, MA 02138, USA;
4. 北京青檬艾柯科技有限公司, 北京 102249;
5. 北京联合大学 应用文理学院, 北京 100191
2. College of Science, China University of Petroleum, Beijing 102249, China;
3. Harvard SEAS-CUPB Joint Laboratory on Petroleum Science, Cambridge MA 02138, USA;
4. Beijing Limecho Technology Limited Company, Beijing 102299, China;
5. College of Applied Arts and Science of Beijing Union University, Beijing 100191, China
以长城为代表的古建筑是人类历史上的重大奇迹和智慧结晶.因其年代久远,建筑材料大多受到了严重的风蚀和老化,导致其内部材质、孔隙结构等发生了变化.因此,如何在完全不破坏其结构的前提下,观测其材质、内部结构、孔隙度等的变化,进而分析获得丰富而独特的相关信息,对研究以长城为代表的古建筑的历史和相应时期的科学技术水平以及如何对其进行更好的保护等方面,都具有重要价值和意义.
核磁共振(NMR)探测技术在多孔介质的研究中具有重大意义,能够有效观测介质内部材质和孔隙结构等,十分适用于古建筑建材的探测和研究.但是,在进行该类研究时,因其研究对象的特殊性,所采用的NMR探测器至少需要其具有三种探测模式:第一种是移动探测模式,直接测量在长城等古建筑墙壁上的城砖等建材,以确定测量取样的位置;第二种模式为长距离探测模式,测量城砖等建材样品内不同层的孔隙结构等信息;第三种探测模式为均匀磁场探测模式,测量城砖样品的总体孔隙结构等信息.
自NMR现象被发现以来,已经过60余年的发展.传统NMR探测仪器通常采用封闭式超导线圈结构,虽然保证了仪器较高的信噪比,但是同时也限制了被测样品的体积和其所处的空间位置.在探测古建筑的建材这一类研究中并不适用.而基于“inside-out”[1, 2]这一理念而设计发展的单边NMR探测器,相比于传统NMR探测装置的最大优势为被测样品的体积大小与所处空间位置不再受到磁体体积的限制,因此能够适用于本研究.
20世纪90年代至今,单边NMR探测器迅速发展,多种不同结构不同类型的探测器纷纷问世.这些探测器根据其采用磁体结构的不同大致可分为两类.第一类探测器采用能够产生较强磁场梯度的磁体结构[3-5],用于梯度磁场条件下的核磁共振检测,如U型磁体结构和条形磁体结构等.第二类探测器所采用的磁体结构经过特殊设计[6-8],所产生的磁场在一定区域内磁场强度分布近似均匀,用于均匀磁场条件下的NMR检测.此外单边NMR探测器具还具有重量轻、体积小等优点,目前已在生物学[9]、化学[10]、医学[11]、考古学[12, 13]和石油工业[14]等领域中得到了广泛的应用.
但是,现有的单边NMR探测器因其磁体结构的原因,均只具有一种探测模式.例如,在设计单边NMR探测器时,要求便于移动,则其磁体质量较小,所产生的静磁场强度也较弱,并且其产生的静磁场分布形式固定,或单一为梯度分布或单一为均匀分布,不能发生变化.而测量环境发生改变,需改变探测器的探测性能参数(静磁场梯度大小、静磁场强度等),来实现探测时,就需改变磁体结构来达成这一目的.因此,若采用现有单边NMR探测器来进行古建筑建材的研究探测,则需要多个探测器来达到所需的三种探测模式,而携带多个探测器对研究工作造成了极大的不便.
因此,我们设计了一种能够满足上述所有探测模式的组合式磁体结构.首先将磁体进行模块化设计,然后通过组合不同的磁体模块,可得到适用于移动探测模式、长距离探测模式和均匀磁场探测模式的磁体结构.
1 磁体设计与模拟仿真 1.1 磁体静磁场计算本文中磁体的静磁场计算采用标量磁位法[15]与有限元方法[16]相结合,可得如下有限元方程:
| $\mathit{\boldsymbol{R}}=\mathit{\boldsymbol{K}}\varphi $ | (1) |
| ${{K}_{ij}}={{\int }_{V}}\mu \nabla {{N}_{i}}\cdot \nabla {{N}_{j}}\text{d}V,\text{ }i,j\in 1,2,3,\cdots ,10$ | (2) |
| ${{R}_{i}}={{\int }_{S}}\mathit{\boldsymbol{n}}\cdot {{\mathit{\boldsymbol{B}}}_{r}}{{N}_{i}}{\rm d}S,\ \ \ \ i \in 1,2,3,\cdots ,6$ | (3) |
(1) ~(3) 式中n为磁体表面外法向的单位向量,
Halbach磁体结构[17-20]是一种能够在其空腔内产生近似均匀的静磁场的磁体结构,并且在产生同等强度的静磁场时Halbach磁体结构较其他磁体结构的总体重量更轻,因而受到广泛关注.但其结构为封闭式结构,不能应用于单边NMR探测器,因此设计时,采用了Halbach磁体结构的一种变种结构——semi-Halbach磁体结构[21]作为其基础磁体结构.这种结构在继承了Halbach磁体结构重量较轻这一优点的同时,还具有足够的外部空间,便于与其他磁体结构进行组合.此外,通过优化设计,能够使其静磁场在目标区域内水平方向上分布近似均匀,竖直方向上磁场梯度近似不变.
因此,本文所设计的探测器磁体系统以上述的semi-Halbach磁体结构为基础,将其设计为三个模块.通过组合的方式,该磁体系统能够得到对应上述三种探测模式的静磁场分布.其中,组合模式1为移动探测模式,组合模式2为长距离探测模式,组合模式3为“均匀场”探测模式(图 1).

|
图 1 探测以长城为代表的古建筑建筑材料时所需的三种探测模式 Figure 1 Three detection modes for detecting the ancient architectures such as the Great Wall |
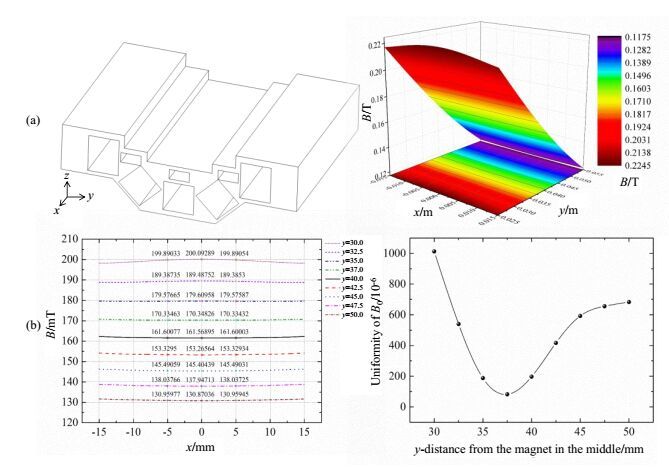
Semi-Halbach磁体结构虽然具有上述优势,但其产生的静磁场强度在磁体设计的目标区域内较弱,直接导致了其探测深度过浅,因此本文中采用了“紧缩场”的相关原理对其进行了优化设计:采用一组能够与semi-Halbach磁体结构产生的静磁场方向相同的U形磁体与其进行组合.在这种组合后的结构中,U形磁体组与semi-Halbach磁体组之间存在强斥力,所产生的静磁场会被逼迫向其上表面的方向,并且semi-Halbach磁体也会在该方向产生静磁场,即该结构所产生的静磁场在某种意义上在其上表面方向被聚焦和集中.因此,组合后的磁体结构较之组合前单一的semi-Halbach磁体所产生的静磁场具有更高的磁场强度和更大的目标区域体积,其结构如图 2(a)所示.
|
图 2 (a)组合模式1的磁体结构,与其静磁场分布;(b) z方向上不同深度水平面上10 mm范围内静磁场强度和磁场均匀度 Figure 2 (a) Structure and simulation result of magnets in mode 1; (b) The intensity and uniformity of B field in 10 mm on lateral planes |
随后采用Gram-Schmidt正交化拟合的方法[22]对组合后的磁体组件进行优化.将semi-Halbach磁体结磁体中心点等弧长摆放在一椭圆曲线上,令黑色磁体组位置固定不变,在设椭圆半长轴为a、半短轴为b,此时,添加约束条件令
| ${{P}_{n}}={{x}^{n}}-\sum\nolimits_{j=0}^{n-1}{{{\alpha }_{jn}}{{P}_{j}}(x),}\text{ }n=0,1,\cdots ,k$ | (4) |
| ${{\alpha }_{jn}}=\frac{\sum\nolimits_{i=0}^{k}{{{x}^{n}}{{P}_{j}}({{x}_{i}})}}{\sum\nolimits_{i=0}^{k}{P_{j}^{2}({{x}_{i}})}},\text{ }j=0,1,\cdots ,n-1;\text{ }n=0,1,\cdots ,k$ | (5) |
则拟合系数和拟合方程分别为:
| ${{\alpha }_{j}}=\frac{\sum\nolimits_{i=0}^{k}{{{f}_{i}}{{P}_{j}}({{x}_{i}})}}{\sum\nolimits_{i=0}^{k}{P_{j}^{2}({{x}_{i}})}},\text{ }j=0,1,\cdots ,k$ | (6) |
| $y=\sum\nolimits_{j=0}^{k}{{{\alpha }_{j}}{{P}_{j}}({{x}_{i}})}$ | (7) |
拟合后经计算分析,确定其极值点,即可得到最佳的优化效果.
对上述设计进行模拟仿真,可得如下结果.组合模式1的磁体结构[图 2(a)]所产生的静磁场B0在磁体正上方的水平面上分布近似均匀.选取z方向上不同深度的水平面,在其上10 mm范围内对静磁场强度进行标注,根据所得数值,对各水平面上的磁场均匀度进行计算,可得到其磁场均匀度分布曲线,如图 2(b)所示,根据该曲线,组合模式1的最佳探测区域为距离其表面35~40 mm之间.
1.2.2 组合模式2的磁体结构设计与模拟仿真组合模式2为长距离探测模式,更远的探测距离意味着所需的静磁场更强.因此,如何在不显著增加磁体质量的同时达到增强磁场的目的为本设计的重点.采用之前所述“紧缩场”的设计理念可达到该效果.因此,组合模式2采用另一组与模式1产生相同方向静磁场的semi-Halbach磁体与模式1的组合即可满足设计需求,该模式的设计计算中,将模式1的磁体设为固定值,采用前述拟合方式对新引入的semi-Halbach磁体进行计算,即可得到模式2的详细参数.
根据计算结果,模式2产生的静磁场相比于模式1具有更高的磁场强度和更大的目标区域体积,模拟仿真结果如图 3(a)所示.在z方向上20 mm范围内不同深度水平面上对静磁场强度进行标注,如图 3(b)所示,根据该标注结果计算分析,组合模式2的最佳探测区域在距离磁体表面42.5~55 mm之间.

|
图 3 (a)组合模式2的磁体结构,与其静磁场分布;(b) z方向上不同深度水平面上20mm范围内静磁场强度和磁场均匀度 Figure 3 (a) Structure and simulation result of magnets in mode 2; (b) The intensity and uniformity of B field in 20 mm on lateral planes |
本文所设计的组合模式3的磁体结构对应均匀磁场探测模式,其产生的静磁场应在其上表面方向上一定区域内分布近似均匀,即该区域内的磁场梯度较小.此外,该模式的测量对象为岩石和城砖类样品,2 MHz的工作频率为测量岩石样品的最佳工作频率,因此将磁场强度的设计目标定为0.047 T.采用一充磁方向相反的条形磁体与模式2中引入的semi-Halbach磁体模块组合可达到该效果,条形磁体的磁场强度和其与semi-Halbach磁体模块之间的相对位置决定了探测深度的深浅,模拟仿真结果如图 4所示.模式3所产生的静磁场在其表面正上方一定区域内分布近似均匀,该区域轮廓近类似于X形.

|
图 4 组合模式3的磁体结构与其静磁场分布 Figure 4 Structure and simulation result of magnets in mode 3 |
综上所述,分别对应以上三种组合模式的磁体结构的详细参数如表 1所示.需要注意的是,所述的中心点位置并不等同于探测深度,而是最佳测量区域的中心点位置距离中间磁体的上表面的位置.当使用组合模式1时,其目标区域体积约为30×30×30 mm3,最佳探测位置的中心点位于磁体中心表面正上方约37.5 mm处,该点的磁场强度约为170.5 mT,磁场梯度约为3.25 T/m,目标区域内不同探测深度的平面上10 mm范围内静磁场均匀度最好可达到185.9×10-6.当使用组合模式2时,目标区域体积约为模式1的4.6倍,其大小为50×50×50 mm3,最佳测量区域的中心点位于磁体中心表面正上方约50 mm处,该点处磁场强度约为189.3 mT,磁场梯度约为3.91 T/m,该模式下,目标区域内不同探测深度平面上20 mm范围静磁场均匀度最好可达到97.9×10-6.当使用组合模式3时,目标区域的形状接近于X形,区域的中心点位于磁体中心表面正上方约37 mm处,该点处静磁场强度约为46.7 mT.
| 表 1 模拟计算得到的三种探测模式详细参数 Table 1 The parameters of all the 3 modes by simulation |
根据上述设计对实物进行了加工制作.其中组合模式1的磁体结构重量约为8 kg,能满足便携测量的要求,通过标准样品对其进行刻度,其最大探测距离约为距磁体表面50 mm.将它与另一个外部磁体模块相组合后即可得到组合模式2——长距离探测模式的磁体结构,其重量约为25 kg,采用标准样品对其进行刻度,其最大探测距离约为距磁体表面78 mm.同样,将组合模式2中所用的外部磁体模块与另一反向充磁的条形磁体模块组合即可得到组合模式3——均匀磁场探测模式的磁体结构,其重量约为22 kg,采用标准样品对其进行刻度,其探测区域为以距磁体表面37 mm处为中心的直径为10 mm范围的X型空间.
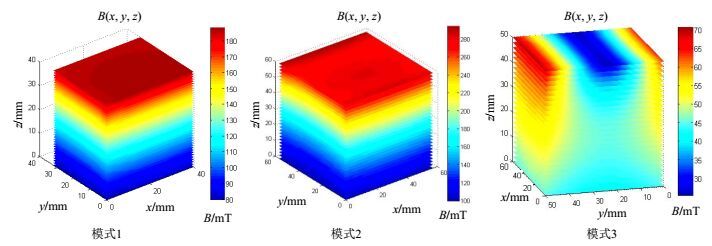
采用CH-3600型高精度三维高斯计对三种实物模型所产生的静磁场的测量.为保证测量精度,测量时设置高斯计的探头运动速度为0.5 cm/s,步长为0.1 mm,稳定时间为1.5 s.其结果如图 5所示.将该结果与模拟计算结果相比较,模拟计算结果较测量值稍大,但静磁场整体分布形态不变,不会影响实际应用效果.模拟计算值比测量值稍大的原因可能为:
|
图 5 三种组合模式的磁体结构所产生的静磁场实测结果 Figure 5 The measured B0 of the 3 modes |
(1)模拟仿真计算所用的磁感应矫顽力Hcb值为1 000 kA/m,而实际加工得到的磁体之间存在一定差异性,其Hcb值不保证为精确的1 000 kA/m.
(2)测量所采用的三维高斯计的位移平台在进行x,y,z三个方向上的移动时存在一定误差.
3 实验分析本研究的主要内容为磁体设计,因此为了进一步验证该磁体设计的合理性和可行性,制作了一组高精度射频线圈与三种磁体组合模式相对应,并进行实验验证.首先测量流体弛豫性质的以验证磁体设计的合理性,之后选测量岩石样品以验证测量砖石的可靠性.
3.1 流体样品测量本实验中,选取横向弛豫时间(T2)约为1 259 ms的油样,将射频线圈调试匹配后采用CPMG[23-25]序列进行测量.测量时采用的回波时间为200 μs,回波个数为20 000,模式1和模式2的扫描次数为16,模式3为64次.
首先应用移动探测模式——组合模式1进行实验,选取其最佳探测区域为工作区域,对应的工作频率为7.0 MHz.随后应用组合模式2进行测量时,因其对应的模式为长距离探测模式,为证明其能够在探测距离较深时正常工作,所选择的测量区域为较深的位置而不是最佳探测区域,该位置处所对应的工作频率为7.2 MHz.最后应用组合模式3进行同样的实验,其探测区域内工作频率为1.9 MHz.
图 6为利用三种磁体组合模式后分别测得的回波串数据.对三个回波串的数据进行反演,采用组合模式1时测得的T2约为857 ms,采用组合模式2所测得T2约为836 ms,采用组合模式3所测得T2约为1 129 ms.

|
图 6 利用上述三种磁体组合模式进行流体测量实验和所测得的回波串数据 Figure 6 The echo train of oil sample measured by the 3 modes |
由流体实验的反演结果可知:组合模式3测得的结果与标准值对应较好,由组合模式1与组合模式2测得的T2较标准值略小,其原因为与这两个模式对应的探测模式均为梯度磁场探测模式,主要用来进行扩散系数等的测量,而在磁体具有较强梯度时测得的T2反演结果需要进行修正,此外减小测量参数中的回波时间(TE)大小可有效降低梯度的影响.
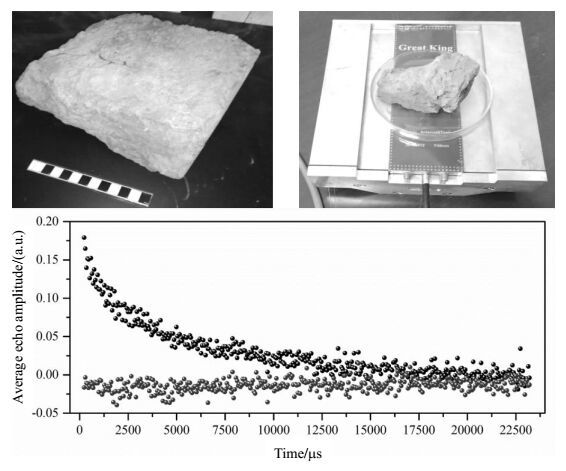
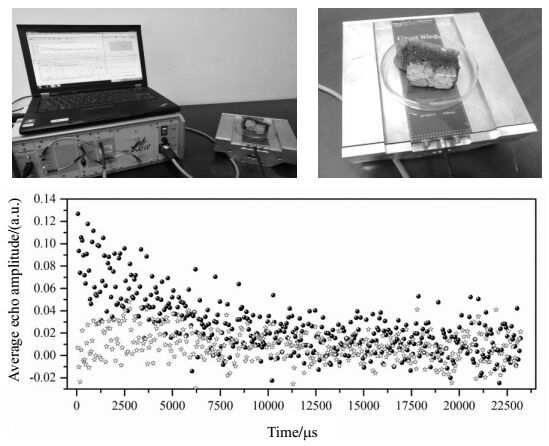
3.2 砖石样品测量为证明本文所设计的磁体系统能够适用于古建筑建材的检测研究,选用了来自于古长城城砖作为样品,对其进行NMR实验测试.采用探测模式为模式1,实验参数为:回波时间58 μs,回波个数400,对应的工作频率为7.05 MHz.实验结果如图 7所示.随后选取现代红砖作为对照样品,采用相同的实验参数进行NMR测量,实验结果如图 8所示.
|
图 7 长城城砖样品NMR测量 Figure 7 NMR measurement for brick from the Great Wall |
|
图 8 现代红砖样品NMR测量 Figure 8 NMR measurement for modern brick sample |
由上述两实验的实验结果对比分析可知:测量长城城砖所得到的回波串衰减较慢,测量红砖样品所得到的回波串衰减迅速,可知长城城砖的孔隙尺寸较现代红砖更大;测量长城城砖所得到的回波串幅值较高,测量现代红砖样品所得到的回波串幅值较低,可知在敏感区域内长城城砖的含水量更大,综合上述可知长城城砖经过多年长期固结定型;现代红砖内铁离子含量较大,顺磁性物质含量丰富,在外加磁场的作用下具有很强的内部梯度场,导致了回波信号的迅速衰减.
4 结论将单边NMR技术应用于文物保护及考古领域是一个较新的研究方向,NMR因其无损探测方式在这些领域凸显独特优势.NMR新应用技术的开发需依托探测仪器的创新,本文以古建筑外表面材料风化程度及工艺探测为目标,开展特种NMR探头磁体结构研究,形成满足多探测方式下的三套磁体方案,并进行了数值模拟和实验测试研究,根据数值模拟成功设计了一种新型单边NMR探测器的组合式磁体,为以长城为代表的古建筑的建筑材料探测和研究奠定了基础.该磁体通过不同磁体模块间的组合,实现三种探测模式[26, 27].其中组合模式1的磁体结构对应移动探测模式,其重量约为8 kg,可以用来直接测量建筑物上的样品等.组合模式2的磁体结构对应长距离探测模式,重量约为25 kg,可用来测量厚度较大的样品,如砖块等.组合模式3的磁体结构对应均匀磁场探测模式,重量约为22 kg,其目标区域内静磁场梯度小于0.1 T/m.模式1和模式2为梯度磁场,场强较高,能够采用的最小回波时间为55 μs,而模式3为均匀磁场探测模式,场强较低,在射频线圈系统没有添加泄放电路的情况下,能够采用的最小回波时间为150 μs.
对上述三种模式的磁体结构所产生的静磁场进行实际测试,测试结果与模拟结果稍有差距,但不影响实际应用效果,后续的流体样品实验以及长城城砖和现代红砖样品实验也证明了磁体设计的合理性和可靠性.
| [1] | COOPER R K, JACKSON J A. Remote (inside-out) NMR. I. Remote production of a region of homogeneous magnetic field[J]. J Magn Reson, 1980, 41(3): 400-405. |
| [2] | JACKSON J A. Nuclear magnetic resonance well logging[J]. Log Analyst, 1984, 25(5): 16-30. |
| [3] | CHANG W H, CHEN J H, HWANG L P. Single-sided mobile NMR with a Halbach magnet[J]. Magn Reson Imaging, 2006, 24(8): 1095-1102. DOI: 10.1016/j.mri.2006.04.005. |
| [4] | EIDMANN G, SAVELSBERG R, BLUMLER P, et al. The NMR MOUSE, a mobile universal surface explorer[J]. J Magn Reson, 1996, 122(1): 104-109. DOI: 10.1006/jmra.1996.0185. |
| [5] | PRADO P J. Single sided imaging sensor[J]. Magn Reson Imaging, 2003, 21(3, 4): 697-400. |
| [6] | KLEINBERG R L, SEZGINER A, GRIFFIN D D, et al. Novel NMR apparatus for investigating an external sample[J]. J Magn Reson, 1992, 97(3): 466-485. |
| [7] | MARBLR A E, MASTIKHIN I V, COLPITTS B G, et al. A constant gradient unilateral magnet for near-surface MRI profiling[J]. J Magn Reson, 2006, 183(2): 78-87. |
| [8] | MANZ B, COY A, DYKSTRA R, et al. A mobile one-sided NMR sensor with a homogeneous magnetic field:the NMR-MOLE[J]. J Magn Reson, 2006, 183(1): 25-31. DOI: 10.1016/j.jmr.2006.07.017. |
| [9] | MCDONALD P J, AKHMEROV A, BACKHOUSE L J, et al. Magnetic resonance profiling of human skin in vivo using GARField magnets[J]. J Pharm Sci, 2005, 94(8): 1850-1860. DOI: 10.1002/jps.20401. |
| [10] | PERLO J, CASANOVA F, BLUMICH B. Ex situ NMR in highly homogeneous fields:1H spectroscopy[J]. Science, 2007, 315(5815): 1110-1112. DOI: 10.1126/science.1135499. |
| [11] | DIAS M, HADGRAFT J, GLOVER P M, et al. Stray field magnetic resonance imaging:a preliminary study of skin hydration[J]. J Phys D Appl Phys, 2003, 36(4): 364-368. DOI: 10.1088/0022-3727/36/4/306. |
| [12] | BLUMICH B, PERLO J, CASANOVA F. Mobile single-sided NMR[J]. Prog Nucl Mag Res Sp, 2008, 52(4): 197-269. DOI: 10.1016/j.pnmrs.2007.10.002. |
| [13] | ZALESSKIY S S, DANIELI E, BLUMICH B, et al. Miniaturization of NMR systems:Desktop spectrometers, microcoil spectroscopy, and "NMR on a chip" for chemistry, biochemistry, and industry[J]. Cheminform, 2014, 45(11): 5641-5694. |
| [14] | COATES G R, XIAO L Z, PRAMMER M. NMR Logging Principles and Applications[M]. USA: Gulf Professional Publishing, 1999. |
| [15] |
LIU F G, YANG Q X. Magnetic scaler potential finite element method applied in 3-D permanent magnetic fields[J].
Journal of Hebei University of Technology, 1997, 3: 49-54.
刘福贵, 杨庆新. 三维永久磁铁磁场的标量磁位数值计算[J]. 河北工业大学学报, 1997, 3: 49-54. |
| [16] | 金建铭. 电磁场有限元方法[M]. 西安: 西安电子科技大学出版社, 1998. |
| [17] | HALBACH K. Strong rare earth cobalt quadrupoles[J]. IEEE T Nucl Sci, 1979, 26(3): 3882-3884. DOI: 10.1109/TNS.1979.4330638. |
| [18] | SOLTNER H, BLUMER P. Dipolar Halbach magnet stacks made from identically shaped permanent magnets for magnetic resonance[J]. Concept Magn Reson A, 2010, 36A(4): 211-222. DOI: 10.1002/cmr.a.v36a:4. |
| [19] | WINDT C W, SOLTNER H, VAN D D, et al. A portable Halbach magnet that can be opened and closed without force:the NMR-CUFF[J]. J Magn Reson, 2011, 208(1): 27-33. DOI: 10.1016/j.jmr.2010.09.020. |
| [20] | ANFEROVA S, ANFEROV V, ADAMS M, et al. Construction of a NMR-MOUSE with short dead time[J]. Concept Magn Res, 2002, 15(1): 15-25. DOI: 10.1002/cmr.v15:1. |
| [21] |
HE W, HE X L, XU Z, et al. The Gram-Schmidt data fitting method for the designing of the gradient magnetic field of unilateral NMR[J].
Journal of Chongqing University (Natural Science Edition), 2013, 36(1): 86-91.
何为, 何晓龙, 徐征, 等. 单边核磁共振磁体梯度磁场设计的Gram-Schmidt正交化拟合方法[J]. 重庆大学学报(自然科学版), 2013, 36(1): 86-91. |
| [22] | Institute for Applied Physics. Dielectric properties of body tissues[EB/OL].[2011-01-28]. http://niremf.ifac.cnr.it/tissprop/. |
| [23] | CARR H Y, PURCELL E M. Effects of diffusion on free precession in nuclear magnetic resonance experiments[J]. Phys Rev, 1954, 94(3): 630-638. DOI: 10.1103/PhysRev.94.630. |
| [24] | MEIBOOM S, GILL D. Modified spin echo method for measuring nuclear relaxation times[J]. Review of Scientific Instruments, 1958, 29: 668-691. |
| [25] | CALLAGHAN P T. Principles of magnetic resonance microscopy[M]. Oxford: Clarendon Press, 1991. |
| [26] | SUN Z, XIAO L Z, LIAO G Z, et al. A modular single-sided NMR sensor design with multifunction[C]. Bologna Italy:13th International Bologna Conferenceon Magnetic Resonance in Porous Media, 2016. |
| [27] | SUN Z, XIAO L Z, ZHANG Y, et al. A modular and multi-functional single-sided NMR sensor[J]. Micropor Mesopor Mat, (in press). DOI:http://doi.org/10.1016/j.micromeso.2017.05.039. |
 2017, Vol. 34
2017, Vol. 34 
