2. 上海卡勒幅磁共振技术有限公司, 上海 201614;
3. 西门子医疗 东北亚科研合作部, 上海 201318;
4. 上海健康医学院, 上海 201318;
5. 广州市番禺区中心医院放射科, 广东 广州 511400
2. Shanghai Colorful Magnetic Resonance Technology Co. Ltd., Shanghai 201614, China;
3. MR Collaboration NE Asia, Siemens Healthcare, Shanghai 201318, China;
4. Shanghai University of Medicine & Health Sciences, Shanghai 201318, China;
5. Department of Radiology, Panyu Center Hospital of Guangzhou, Guangzhou 511400, China
磁共振成像(MRI)是当今最重要的医学影像方法之一,它的主要弱点是信号灵敏度较低、图像信噪比较差.在低场MRI系统或使用一些特殊的成像序列时,这一问题显得尤为严重.解决这一问题最常用的方法是进行多次图像采集并进行相干平均.但如果在图像扫描过程中人体发生自主或不自主的运动,相干平均会导致图像边缘模糊.例如,在我们利用扩散方法对肝脏进行研究时,由于横向弛豫时间(T2)较大、信号衰减快,同时扩散加权因子(b)进一步造成信号衰减,导致图像的信噪比较低;而进行多次扫描相干平均时,由于肝脏受呼吸和心脏运动的影响,每次扫描获得的图像间存在位移与形变,简单的相干平均的结果也难以令人满意.
提高磁共振图像信噪比的另一个方法是图像去噪.图像去噪对MRI系统硬件没有额外的要求,也不会增加MRI扫描时间,因此一直是磁共振图像处理领域的热门问题[1, 2],研究者已经提出了多种不同的算法用于磁共振图像的去噪处理[3-9].其中,2005年由Buades等人[10]基于自然图像存在自相似性(即图像中相似的结构应该有相似的灰度值),提出的非局域均值(NLM)算法取得了良好的去噪效果.该算法思想简单,效果却很好,引起了广泛的关注,也取得了很大的发展[11-16].
对于处理信噪比很差的图像,图像去噪方法的主要问题是,由于单幅图像中包含的信息有限,限制了图像去噪算法的最终效果.因此,要提高信噪很低且不同次采样之间存在运动的图像的信噪比,需要新的思路.针对这一问题,本文受NLM算法图块匹配思想[17-19]的启发,提出了一种新的算法.该算法通过比较多次采集的图像中组织结构的局部相似性,找出图像间的局部位移;利用该信息修正位移;然后对多幅图像进行加权平均,从而达到提高图像信噪比的目的.我们利用模拟与真实的磁共振图像进行了实验,将本文算法与简单的相干平均以及传统的NLM去噪算法进行了比较,结果表明,本文算法可以有效地提高图像的信噪比,并较好地保持图像细节.
1 理论与方法 1.1 NLM滤波NLM算法[10]认为具有相似邻域的像素会有相似的灰度值,通过计算其他像素邻域与目标像素邻域的欧几里德距离,可以得到两个像素邻域的相似性,进而根据此相似性计算其他像素值对目标像素值的权重,最后将所有像素做加权平均得到新的目标像素的值.
假设图像I(i)由真实信号X(i)与噪声n组成:
| $I\left( i \right) = X\left( i \right) + n$ | (1) |
则NLM滤波后的一个点的灰度值为:
| $NL(i) = \sum {_{j \in I}} \omega (i,j)I(j)$ | (2) |
其中:
| $\omega (i,j) = \frac{1}{{Z(i)}}{{\rm{e}}^{ - \frac{{\left\| {I({N_i}) - I({N_j})} \right\|_{2,\alpha }^2}}{{{h^2}}}}}$ | (3) |
| $Z(i) = \sum {_{j \in I}} {{\rm{e}}^{ - \frac{{\left\| {I({N_i}) - I({N_j})} \right\|_{2,\alpha }^2}}{{{h^2}}}}}$ | (4) |
其中,h为指数函数的衰减因子,控制指数函数衰减的快慢;Ni表示以i点为中心的一定大小的方形邻域;ω(i, j)为像素j对像素i的权重;Z(i)是权重归一化系数.为了突出强调离图像块中心越近的点对两个图像块相似性的贡献越大,我们给图像块各点加上一个高斯权重,α>0是高斯加权的标准差.
从NLM算法的计算公式中我们也可以看出,图像中的某个像素滤波后的灰度值是图像中其他像素灰度值的加权平均,权重由两个像素的邻域块的欧几里德距离决定.两个像素的邻域块的欧几里德距离越小,说明这两个像素的邻域块的相似度越大,因此在计算权重时所占的权重越大.
1.2 基于局部位移校正的相干平均磁共振图像容易受到运动的影响,这也是心脏、腹部等MRI所需要面临的主要困难之一.例如进行扩散加权成像研究时[20, 21],由于使用了较高的b值,导致图像的信噪比很低,需要通过相干平均来改善图像的信噪比.但是由于图像采集的过程中难免发生身体的运动,多次采集的图像之间存在位置偏移,将这些有偏移的图像直接相加,会造成图像边缘模糊.本文算法的第一步,就是要找出这些偏移.
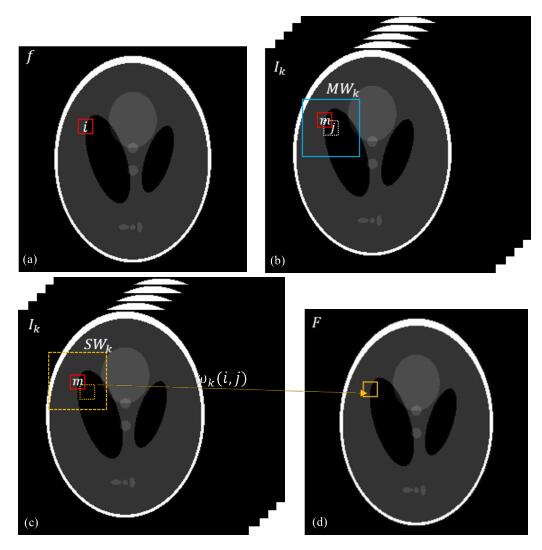
我们用来确定图像局部偏移的方法,借鉴了NLM算法中图块匹配的思想[17-19].假设以图像系列中的某一幅图像f为参考图像,确定采集的其他图像Ik中的偏移量的方法是,对于参考图像中的某一像素i[如图 1(a)所示],在图像Ik中的对应像素i附近的一个匹配窗范围MWk内[如图 1(b)所示],寻找与参考图中i的邻域图块最相似的图块,即优化下式的结果:
| $m = \mathop {\arg \min }\limits_{j \in M{W_k}} \left\| {f({N_i}) - {I_k}({N_j})} \right\|_2^2$ | (5) |
|
图 1 本文算法方案图 Figure 1 Scheme of the proposed method |
找到最匹配像素后以该像素为中心做一定大小的搜索范围[如图 1(c)所示],对图像系列的每一幅图像相应搜索窗内的邻域像素块做非局域均值加权平均[如图 1(d)所示],具体计算公式为:
| $F(i) = \sum {_k} \sum {_{j \in S{W_k}}} {\omega _k}(i,j){I_k}(j)$ | (6) |
| $\omega (i,j) = \frac{1}{{Z(i)}}{{\rm{e}}^{ - \frac{{\left\| {f({N_i}) - {I_k}({N_j})} \right\|_{2,\alpha }^2}}{{{h^2}}}}}$ | (7) |
| $Z(i) = \sum {_k} \sum {_j} {{\rm{e}}^{ - \frac{{\left\| {f({N_i}) - {I_k}({N_j})} \right\|_{2,\alpha }^2}}{{{h^2}}}}}$ | (8) |
其中,SWk为在第k幅图像中以结构最匹配点Ik(m)为中心的搜索范围内的像素.
实际操作中,用上述方法做NLM加权平均时利用到的方形邻域块数目太多,假设搜索窗大小为sw,图像系列一共有l幅图像,那么我们用来做NLM加权平均的邻域块数为l×sw2.邻域块过多会导致过多结构完全不匹配的点对当前点的值做出贡献,从而引入伪影.因此我们对要用来做加权平均点的数量加以限制[22],当两个邻域像素块的欧几里德距离大于参考图像噪声水平方差(
| ${\omega _k}(i,j) = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{Z(i)}}{{\rm{e}}^{ - \frac{{\left\| {f({N_i}) - {I_k}({N_j})} \right\|_{2,\alpha }^2}}{{{h^2}}}}},}\\ {0,\quad \quad \quad otherwise} \end{array}} \right.\left\| {f({N_i}) - {I_k}({N_j})} \right\|_{2,\alpha }^2 < tol \times \sigma _{ref}^2$ | (9) |
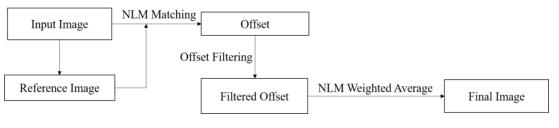
由于发生运动的组织结构的整体性,我们找出的偏移量在空间上应该是连续的,相邻像素的偏移量应该接近.由于噪声的影响,可能导致寻找最匹配结构时获得了错误的偏移量.为了消除这一问题的影响,我们对图像的偏移量进行了中值滤波.即对于每一幅图像,利用图块匹配的方法,寻找参考图像中的每个像素i在当前图像中在水平与垂直两个方向上的偏移量offsetx(i)和offsety(i),最后分别对offsetx和offsety做中值滤波.将中值滤波结果作为最匹配像素的位置,再进行NLM加权平均.我们把这个方法叫做匹配加权平均(MWA),该方法流程图如图 2所示.
|
图 2 MWA算法流程图 Figure 2 Flowchart of the proposed MWA method |
为了验证本文算法位移校正的效果,利用BrainWeb[23]提供的大小为217×181的无噪声T1加权磁共振脑图,周围填零后得到大小为256×256的图像,将此图像作为金标准图像[图 3(a)].随后将金标准图像整体分别向左上移动0、2、4、6、8和10个像素,得到6张图像,每张都加上均值为0、方差为0.002的高斯噪声,图 3(b)为移动0个像素的带噪图;图 3(c)为简单相干平均图像;图 3(d)为对图 3(b)做单张NLM去噪图像(取最优参数:图像块大小ps = 7,高斯加权标准差α = 2,衰减因子j = 0.05,搜索窗大小sw = 15);图 3(e)为利用结构相似性做位移校正后,直接将位移校正图像做相干平均结果(取最优参数:图像块大小ps = 7,高斯加权标准差α = 2,衰减因子h =0.01,搜索窗大小sw = 21);图 3(f)为利用本文算法处理图像系列结果(取最优参数:图像块大小ps = 7,高斯加权标准差α = 2,匹配窗大小mw = 17,衰减因子h = 0.05,搜索窗大小sw = 17,容差tol = 3.9).

|
图 3 不同去噪算法对带有均值为0、方差为0.002高斯噪声的BrainWeb模拟脑图处理结果.(a)金标准图像;(b) 0位移带噪图(参考图像);(c)简单相干平均图像;(d)对(b)做NLM去噪图像;(e)位移校正后相干平均图像;(f)利用本文提出的算法(MWA)处理后的图像 Figure 3 Results of different methods on noised (zero mean and 0.002 variance Gaussian noise) BrainWeb phantom images. (a) Gold standard; (b) Zero offset noise image; (c) Simple average image; (d) NLM image; (e) Offset corrected image; (f) MWA image |
由于模拟图像的相对位移比较大,因此简单相干平均图像的方法失效,可以看到累加出来的图像非常模糊,这也说明了在做相干平均时对发生运动偏移进行位置校正的重要性.经过位移校正后做累加的图 3(e)和图 3(f)的模糊现象得到了明显的改善,这说明我们利用结构相似性校正位置偏移的方法是有效可行是的,它可以利用不同幅图像的信息保证图像结构边缘锐利.
为了进一步考察图像的去噪效果,我们利用金标准图像分别计算图 3(c)、(d)、(f)的峰值信噪比(PSNR)、平均结构相似度(MSSIM)和残留噪声标准差(SDR),结果如表 1所示.从表中可以看出,本文算法去噪效果优于单张NLM去噪,尤其是MSSIM值远远高于NLM去噪,这说明本文算法成功利用了不同图像中相似结构信息,在提高图像信噪比的同时保证图像结构边缘清晰,提高了图像视觉效果.
| 表 1 不同方法处理结果的PSNR、MSSIM和SDR Table 1 PSNR、MSSIM and SDR values of the MR images processed with different methods |
我们也利用真实的磁共振图像对本文算法与对简单累加以及传统的NLM滤波进行了比较.在NLM算法中图像块及其高斯窗的大小需要选取合适的值,邻域图块太小不能表现出图像结构信息;而邻域图块太大会导致处理后的图像过平滑.因此我们选用5×5邻域像素块、高斯加权标准差α为1.5,以及7×7邻域像素块、高斯加权标准差α为2,这两种我们认为较合理的参数组合.控制指数函数衰减快慢的指数函数衰减因子(h)的大小应该和图像的噪声水平有关,在有关文献[24]中作者选用的h值为10σ~ 15σ,其中σ为噪声方差,但是不同图像的最佳h值不同,许多文献[25, 26]对h大小的计算都做过相关的优化,本文中根据经验和实验情况,h选在0.01~0.5之间,匹配窗的大小mw在15~25个像素之间选取奇数值,搜索窗大小sw将在9~17之间取奇数值.
本实验使用的健康自愿者肝脏扩散加权磁共振图像采集自1.5 T西门子磁共振Espree系统,其中一组图像在采集时加入了自由呼吸心电门控,另一组在图像采集时没有加.采集序列为扩散加权成像序列(DWI),观察视野(FOV)= 350 mm×380 mm;层厚(slice thickness)= 8 mm;层数(slice count)= 1;回波时间(TE)= 60 ms;重复时间(TR)= 350 ms,采样矩阵(matrix)= 98×122.
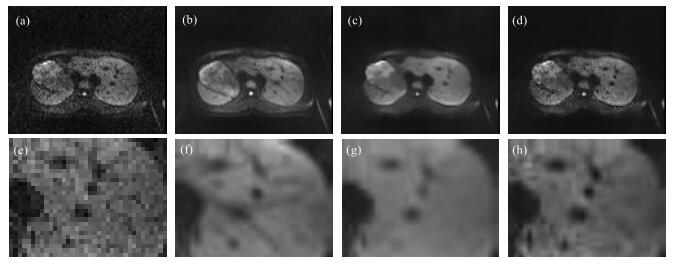
图 4给出了没加自由呼吸门控的肝脏扩散加权图像的处理结果:图 4(a)为图像系列中的第8幅图像,作为我们的方法的参考图像;图 4(b)是对图像系列做简单相干平均后的图像;图 4(c)是对图 4(a)做单张NLM去噪后的图像,这里用的参数如下:图像块大小ps = 5,高斯加权标准差α = 1.5,衰减因子h = 0.07,搜索窗大小sw = 13,这些参数是经过实验找到视觉效果最佳的;图 4(d)为使用本文提出的MWA方法处理出的视觉效果最佳图像,其参数为:图像块大小ps = 5,高斯加权标准差α = 1.5,匹配窗大小mw = 19,衰减因子h = 0.05,搜索窗大小sw = 13,容差tol = 5;图 4(e)~(h)分别是图 4(a)~(d)的局部放大图.从图中我们可以看出,由于图像的噪声水平较高,直接对参考图像做NLM去噪处理的图像过于平滑,而且会有许多伪影;简单相干平均图像信噪比高、图像细节清楚,但是会包含许多参考图像没有的细节,由于人体的运动会采集到不同层图像,简单相干平均会将不同层图像结构加在一起;而使用本文提出的MWA方法处理的图像,虽然看起来图像细节没有简单相干平均的结果多,但其准确反映了参考图像中的结构信息.
|
图 4 无自由呼吸门控肝脏弥散加权图像. (a)为图像系列中的某一幅图像,作为参考图像;(b)简单累加图像;(c)对参考图像做单张NLM去噪后图像;(d)利用本文提出的算法(MWA)得出的图像;(e)~(h)为图(a)~(d)的局部放大图 Figure 4 DWI of liver (without ECG). (a) Reference image (one of 30 images); (b) Simple average image; (c) NLM image; (d) MWA image; (e)~(h) Partial enlarged detail from (a)~(d) |
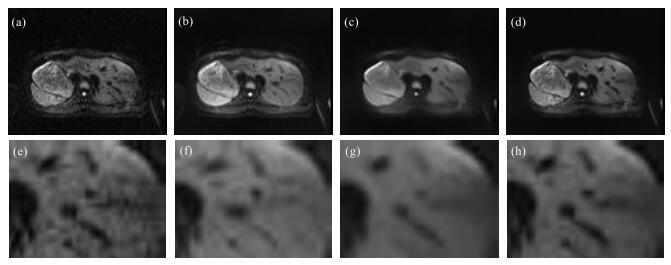
图 5分别给出的是加了自由呼吸门控的肝脏扩散加权图像图,比起没有加自由呼吸门控的图像而言,这一组图像本身的信噪比较高,由于呼吸运动导致的采集到不同层信息的现象会减少,因此不同幅图像间的结构会越接近.图 5(a)为图像系列中的某一幅图像,作为本文提出的MWA方法中的参考图像;图 5(b)是对图像系列进行简单相干平均后的图像;图 5(c)是对5(a)做单张NLM去噪后视觉效果最佳的图像;图 5(d)为使用本文提出的MWA方法得出的视觉最佳图像,其参数为:图像块大小ps = 5,高斯加权标准差α = 1.5,匹配窗大小mw = 21,衰减因子h = 0.05,搜索窗大小sw = 11,容差tol = 5;图 5(e)~(h)为图 5(a)~(d)的局部放大图.从图中我们可以看出,对图像系列做简单累加后的图像中包含一些参考图像中没有的细节,而在单张NLM去噪图像和本文算法处理出的图像中不存在此类问题;从局部放大图中我们可以看出,对图像做简单的NLM去噪能有效去除噪声,一定程度上比做累加的边缘也更锐利,但是损失了一些细节;值得注意的是,在这一组数据上用本文提出的MWA方法处理的图像,不仅能在提高信噪比的同时保留参考图像结构清晰,在视觉效果上也优于做简单相干平均图像.
|
图 5 有自由呼吸门控肝脏弥散加权图像. (a)为图像系列中的某一幅图像,作为参考图像;(b)简单累加图像;(c)对参考图像做单张NLM去噪后图像;(d)利用本文提出的算法(MWA)得出的图像;(e)~(h)为图(a)~(d)的局部放大图 Figure 5 DWI of liver (with ECG). (a) Reference image (one of 30 images); (b) Simple average image; (c) NLM image; (d) MWA image; (e)~(h) Partial enlarged detail from (a)~(d) |
本文针对信噪比较低、又包含运动的磁共振图像难以进行相干平均的情况,提出了一种新的算法——MWA,利用NLM去噪算法和图像块匹配的思想,对各幅图像中同一结构之间的位置偏移进行校正,并利用校正后的图像进行加权平均.实验证明我们提出的方法能够有效提高图像的信噪比,而且保持图像边缘清晰.对于由于运动导致采集到不同层图像信息,本文算法也不会将不同层的图像细节信息混淆在同一幅图像中.
| [1] | MOHAN J, KRISHNAVENI V, GUO Y. A survey on the magnetic resonance image denoising methods[J]. Biomed Signal Proces, 2014, 9(1): 56-69. |
| [2] | JOSHI N, JAIN S. Optimization of nonlocal means filtering technique for denoising magnetic resonance images:A review[C]//Proceedings of fifth international conference on soft computing for problem solving. Singapore:Springer, 2016:1-15. |
| [3] | SAMSONOV A A, JOHNSON C R. Noise-adaptive nonlinear diffusion filtering of MR images with spatially varying noise levels[J]. Magn Reson Med, 2004, 52(4): 798-806. DOI: 10.1002/(ISSN)1522-2594. |
| [4] | LU B B, DENG C, LIU Q, et al. Four order adaptive PDE method for MRI denoising[C]//IEEE ACMT Comput Bi, 2009. |
| [5] | ZHANG F, MA L H. MRI denoising using the anisotropic coupled diffusion equations[C]//20103rd international conference on BMEI. IEEE, 2010, 1:397-401. |
| [6] | MA J, PLONKA G. Combined curvelet shrinkage and nonlinear anisotropic diffusion[J]. IEEE T Image Process, 2007, 16(9): 2198-2206. DOI: 10.1109/TIP.2007.902333. |
| [7] | PARTHIBAN L, SUBRAMANIAN R. Medical image denoising using X-lets[C]//India conference, 2006 Annual IEEE, 2006:1-6. |
| [8] | YANG X, FEI B. A wavelet multiscale denoising algorithm for magnetic resonance (MR) images[J]. Meas Sci Technol, 2011, 22(2): 025803. DOI: 10.1088/0957-0233/22/2/025803. |
| [9] | LUISIER F, BLU T, WOLFE P J. A cure for noisy magnetic resonance images:Chi-square unbiased risk estimation[J]. IEEE T Image Process, 2012, 21(8): 3454-3466. DOI: 10.1109/TIP.2012.2191565. |
| [10] | BUADES A, COLL B, MOREL J M. A review of image denoising algorithms, with a new one[J]. Multiscale Model Sim, 2005, 4(2): 490-530. DOI: 10.1137/040616024. |
| [11] | MANJÓN J V, CARBONELL J, LULL J J, et al. MRI denoising using non-local means[J]. Med Image Anal, 2008, 12(4): 514-523. DOI: 10.1016/j.media.2008.02.004. |
| [12] | HU J R, PU Y F, WU X, et al. Improved DCT-based nonlocal means filter for MR images denoising[J]. Comput Math Methods Med, 2012: 232685. |
| [13] | MANJÓN J V, COUPÉ P, BUADES A, et al. New methods for MRI denoising based on sparseness and self-similarity[J]. Med Image Anal, 2012, 16(1): 18-27. DOI: 10.1016/j.media.2011.04.003. |
| [14] | ZHANG X Y, HOU G R, MA J H, et al. Denoising MR images using non-local means filter with combined patch and pixel similarity[J]. PloS one, 2014, 9(6): e100240. DOI: 10.1371/journal.pone.0100240. |
| [15] | GUO T L, LIU Q G, LUO J H. Filter bank based nonlocal means for denoising magnetic resonance images[J]. Journal of Shanghai Jiaotong University (Science), 2014, 19(1): 72-78. DOI: 10.1007/s12204-014-1476-8. |
| [16] | WIEST-DAESSLÉ N, PRIMA S, COUPÉ P, et al. Rician noise removal by non-local means filtering for low signal-to-noise ratio MRI:Applications to DT-MRI[M]. Berlin: Springer Heidelberg, 2008: 171-179. |
| [17] | BARNES C, SHECHTMAN E, FINKELSTEIN A, et al. PatchMatch:A randomized correspondence algorithm for structural image editing[J]. ACM Graphic, 2009, 28(3): 24. |
| [18] | GIRAUD R, TA V T, PAPADAKIS N, et al. An optimized PatchMatch for multi-scale and multi-feature label fusion[J]. Neuroimage, 2016, 124: 770-782. DOI: 10.1016/j.neuroimage.2015.07.076. |
| [19] | BARNES C, SHECHTMAN E, GOLDMAN D B, et al. The generalized patchmatch correspondence algorithm[M]. Berlin: Springer Heidelberg, 2010: 29-43. |
| [20] | WIEST-DAESSLÉ N, PRIMA S, COUPÉ P, et al. Non-local means variants for denoising of diffusion-weighted and diffusion tensor MRI[M]. Berlin: Springer Heidelberg, 2007: 344-351. |
| [21] | BAO L, ROBINI M, LIU W, et al. Structure-adaptive sparse denoising for diffusion-tensor MRI[J]. Med Image Anal, 2013, 17(4): 442-457. DOI: 10.1016/j.media.2013.01.006. |
| [22] | MANJÓN J V, COUPÉ P, BUADES A, et al. Non-local MRI upsampling[J]. Med Image Anal, 2010, 14(6): 784-792. DOI: 10.1016/j.media.2010.05.010. |
| [23] | http://brainweb.bic.mni.mcgill.ca/brainweb/ |
| [24] | BUADES A, COLL B, MOREL J M. A non-local algorithm for image denoising[C]. IEEE T Comput, 2005, 2:60-65. |
| [25] | COUPÉ P, YGER P, PRIMA S, et al. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images[J]. IEEE T Med Imaging, 2008, 27(4): 425-441. DOI: 10.1109/TMI.2007.906087. |
| [26] | AVANAKI A N, DIYANAT A, SODAGARI S. Optimum parameter estimation for non-local means image de-noising using corner information[C]. IEEE T Signal Proce, 2008:861-863. |
 2017, Vol. 34
2017, Vol. 34 
