2. 中国科学院大学, 北京 100049;
3. 上海科技大学, 上海 201210;
4. 上海联影医疗科技有限公司, 上海 201807
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China;
4. Shanghai United Imaging Healthcare Cooperation, Shanghai 201807, China
心脏磁共振成像(CMRI)因拥有良好的组织对比度及对人体无创无害的特点,近年来被广泛应用于临床研究[1].心脏电影成像(Cardiac CINE imaging)利用心脏运动的自律性将整个心动周期分为若干期相,每个期相(50 ms以内)内心脏运动视为相对静止,采用心电门控(ECG)触发、k空间分段采集的方式在每个心动周期的相同期对图像进行采集,最终得到各个期相的完整图像.把这些图像连续播放形成电影,可以反映一个心动周期内心脏的搏动情况.心脏电影成像技术有着高时间分辨率和高空间分辨率的要求,不仅能测量心脏功能的各项指标,例如射血分数、每搏输出量等,还可以观测心肌的运动情况,判断心肌是否病变[2].
心脏的运动十分复杂,不仅有自身的跳动,而且其位置还会受到呼吸运动的影响,因此在不使用导航的情况下需要屏气扫描才能得到清晰的图像,并且需要受检者高度配合.正常人的屏气时间一般在12~20 s之间,老年人、儿童以及特殊患者的屏气时间更短.目前在临床的常规扫描中,正常人一次屏气时间内只能采集1~2层的电影图像,若要采集心脏的全图像则需要多次屏气,且需包括被试者的休息时间,因此临床常规心脏电影成像扫描时间非常长,容易在成像过程中引入各种运动伪影.为了解决这一问题,临床上通常尝试采用平面内的并行加速(PPA)技术通过减少相位编码数来节省采集时间[3],但相位编码数的减少使得图像的信噪比(SNR)降低,影响了图像质量,并极大的限制了加速的倍数.
2005年,Breuer等[4]提出了相位调制同时多层激发(SMS-CAIPIRINHA,以下简称CAIPIRINHA)技术,这种方法利用合成的射频(RF)脉冲同时激发多个片层,使得一次采集可同时得到多个片层的图像[4].与早前的同时多层激发技术相比,CAIPIRINHA会对合成的射频脉冲的每个成分进行相位调制使得同时激发的每层图像都会有一个相对位移,使线圈的空间灵敏度变化增大,以便使用并行成像的重建原理对多层激发技术进行图像重建,其消除了传统并行成像技术中
在前人研究的基础上,本文将层面间的CAIPIRINHA加速技术和层面内的PPA技术同时结合到基于BSSFP的心脏电影成像序列中,在相位编码和选层编码两个方向同时加速,并利用一种改进的二维加速重建算法,即SENSE/GRAPPA(sensitivity encoding/Generalized autocalibrating partially parallel acqusitions)[9]进行图像重建,在获得更高加速倍数的同时保证图像质量,进一步减弱心率不齐等运动因素对心脏电影成像的影响,减少患者的屏气时间,提高检查的舒适度.
1 实验部分 1.1 实验方法整个成像过程分为两部分:第一步,将多个射频脉冲叠加,调整相位循环和采样的相位编码,集成到心脏电影成像序列中;第二步,利用提前采集的参考图像对双重加速数据进行图像重建,得到无混叠伪影的图像.
1.1.1 序列设计CAIPIRINHA技术的关键之一是将多个射频脉冲经过相位调制后合成一个新的激发脉冲.传统的单层图像信号
| $\rho (y) = \sum\limits_{m = - N/2}^{(N/2) - 1} S (m\Delta k) \times {e^{im\Delta ky}}$ | (1) |
其中S表示一般的k空间信号;采样间距
| $\rho (y) = \sum\limits_{m = - N/2}^{(N/2) - 1} {[\sum\limits_{j = 1}^{NS} {{S_j}(m\Delta k)} ]} \times {e^{im\Delta ky}} = \sum\limits_{j = 1}^{NS} {{\rho _j}(y)} $ | (2) |
此时每层图像会直接叠加在一起,空间灵敏度矩阵也会十分接近,如图 1(a)所示.

|
图 1 同时激发两层时,k空间相位调制示意图.(a)两层都没有经过相位调制的混叠情况;(b)线性相位调制为(0, π)时的混叠情况;(c)线性相位调制为(π/2, -π/2)时的混叠情况 Figure 1 The schematic diagram of simultaneously two-slice k-space phase encoding. (a) Two slices without RF phase encoding; (b) Two slices with (0, π) RF phase encoding; (c) Two slices with (π/2, -π/2) RF phase encoding |
当空间灵敏度矩阵为奇异矩阵时,无法利用并行成像的重建方法解开多层图像的混叠.为了增大图像空间灵敏度矩阵的变化,对激发每层图像的射频脉冲加上特定的线性相位调制,使得每一层图像与其它层在相位编码方向有一个相对位移:
| $\rho (y) = \sum\limits_{m = - N/2}^{(N/2) - 1} {[\sum\limits_{j = 1}^{NS} {{S_j}(m\Delta k){e^{ - i{\Phi _j}(m)}}} ]} \times {e^{im\Delta ky}} = \sum\limits_{j = 1}^{NS} {{\rho _j}(y - \Delta {y_j})} $ | (3) |
其中,
| $\rho {(y)^*} = \sum\limits_{m = - N/2}^{(N/2) - 1} {[{S_1}(m\Delta k) + {S_2}(m\Delta k){e^{ - im{\rm{\pi }}}}]} \times {e^{im\Delta ky}} = \rho _1^*(y) + \rho _2^*(y{\rm{ - }}\frac{{FOV}}{2})$ | (4) |
在具体实现上,通常选定一层作为基准,算出同时激发的片层与基准层的距离Δz.根据
| ${\rho ^*}(y) = \sum\limits_{m = - N/2}^{(N/2) - 1} {[{S_1}(m\Delta k)(1 + {e^{{\rm{i}}2{\rm{\pi }}\Delta f}} \times {e^{ - {\rm{i}}m{\rm{\pi }}}})]} \times {e^{{\rm{i}}m\Delta ky}}$ | (5) |
以上所述只是普通的CAIPIRINHA方法,本文使用的BSSFP序列对B0场不均匀敏感,容易形成带状伪影影响图像质量,可以通过线性增加射频相位来改变共振偏置角抑制带状伪影.为了抑制带状伪影维持稳态,射频相位变化需要满足以下条件[10]:
| $\Phi (m) = A + Bm + C{m^2}$ | (6) |
其中,A、B、C可为任意常数.一般来说线性的相位循环即可维持稳态.因此,在本文中Φ(m)需要同时满足两方面的条件,这意味着前文中CAIPIRINHA的射频相位循环需要作出改变.可取A=C=0、B=ΔkΔy(B≠0),同时满足两方面的条件,只要保证Bj的值各不相同,理论上可以对同时激发的任意一层选取任意的Bj=ΔkΔyj.但实际上,为了最大化空间灵敏度矩阵的变化和重建的准确度,优选的方案是将同时激发的每层均匀的分布在整个视野中.比如同时激发两层时,每层之间有FOV/2的位移、B1=π/2、B2=-π/2、Δy1=FOV/4、Δy2=-FOV/4,(6) 式则近一步变化为:
| $\rho {(y)^*} = \sum\limits_{m = - N/2}^{(N/2) - 1} {[{S_1}(m\Delta k)({e^{\frac{{ - {\rm{i}}m{\rm{\pi }}}}{2}}} + {e^{{\rm{i}}2{\rm{\pi }}\Delta f}} \times {e^{\frac{{ - {\rm{i}}m{\rm{\pi }}}}{2}}})]} \times {e^{{\rm{i}}m\Delta ky}}\\ = \rho _1^*(y - \frac{{FOV}}{4}) + \rho _2^*(y + \frac{{FOV}}{4})$ | (7) |
由于需要维持磁化矢量的稳态,在层面内加速和电影成像时需保持序列相位循环的固定和完整.在层面内加速时因部分相位编码会跳过,需要对线性相位编码进行调整,当加速倍数为R时,若仅在相位编码为R的倍数时进行采样,Φj(m)=Bjm/R=ΔkΔyjm/R, m=0, R, 2R, ….
本文中的心脏电影成像采用ECG触发的分段采集,由于每一幅图像都是分段在多个心动周期中同一期相采集的,这意味着每幅图像的采集过程都会有间断.为了保持相位循环的完整和磁化矢量的稳态,每个期相中包含的相位编码数应是相位循环数的整数倍.
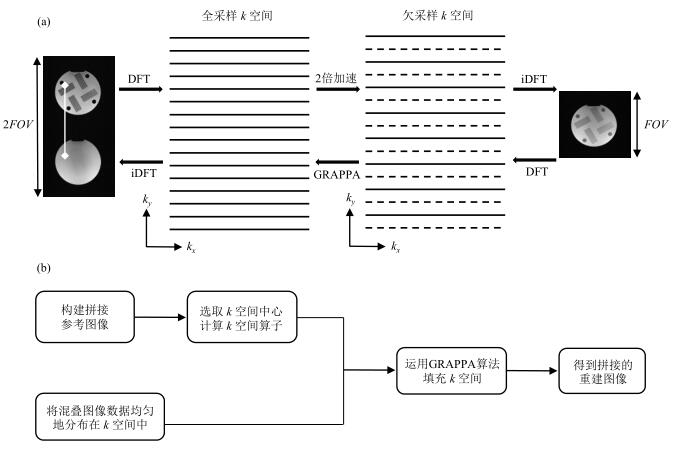
1.1.2 重建方法并行成像的重建方法利用接收阵列固有的空间灵敏度信息来分离欠采样导致的混叠图像信号,其基础算法包括基于图像域的SENSE算法[11]和基于k空间的GRAPPA算法[12].SENSE算法利用参考图像计算出图像灵敏度矩阵,然后将混叠的图像通过灵敏度矩阵反解出完整的图像[11].GRAPPA算法则是利用k空间中心全采样部分计算出k空间的算子,这个算子表示的是k空间中的点与相邻的点的线性关系,利用这种线性关系将欠采样部分的k空间信号通过卷积计算填充后,得到完整k空间的信号[12].标准的SENSE和GRAPPA算法只是对相位编码方向的欠采样进行重建,是一维加速的重建算法.近年来有学者[9]提出了一种SENSE联合GRAPPA的技术可以对二维加速(即相位编码方向和选层方向同时加速)进行图像重建.对于两层同时激发且没有经过相位调制混叠图像的重建,SENSE/GRAPPA技术将两层参考图像拼接在一起,构造一个扩展到二倍FOV的二维图像,将选层方向的信息转换到相位编码方向,使得这个扩展后的图像可以包括所有三维的信息.混叠图像则可视为对拼接图像的二倍欠采样,将混叠图像的k空间数据均匀的分布在二倍FOV的k空间内,利用参考图像所构造的拼接图像的k空间中心数据计算出k空间算子,最后对扩展后混叠图像的k空间数据进行填充,傅里叶变换后得到没有混叠的拼接图像.重建示意及流程如图 2所示.
|
图 2 SENSE/GRAPPA算法示意图.(a)从左往右是拼接图像k空间2倍欠采样后,傅里叶变换可得到混叠图像;而从右往左是将混叠图像的k空间数据均匀分布在2倍视野的k空间中,用k空间算子填充欠采样部分,傅里叶变换后得到一幅两层拼接的没有混叠的图像[13];(b) SENSE/GRAPPA算法的操作流程图 Figure 2 The schematic diagram of SENSE/GRAPPA algorithm. (a) From left to right, k-space undersampling of concatenate image results in aliased image. And from right to left, put aliased image k-space data in 2-flod FOV space uniformly, applying GRAPPA results in concatenate two slices[13]; (b) SENSE/GRAPPA algorithm operation flowchart |
然而对于经过相位调制的多层激发图像,同时激发的两层图像的相位调制并不一致.而SENSE/GRAPPA方法所构造的k空间算子只能适用于相同相位调制混叠图像重建,在相位调制的情况下,标准的SENSE/GRAPPA方法易在图像拼接处造成伪影[13],如图 3(b)所示.其解决方法是对SENSE/GRAPPA算法进行调整,增加一倍FOV[5],利用参考图像在拼接图像中的位置移动模拟混叠图像因相位调制导致的平移,使用相同相位调制的两层参考图像来构建拼接图像,其余部分填零处理,对扩展后的拼接图像三倍欠采样后可以得到同时激发的混叠图像,在保持相位调制一致性的同时使得像素之间的混叠状态仍然和原图像相同.除了上述拼接参考图像的构建有所变化以及因拼接FOV增大所带来的k空间欠采样倍数变化外[图 3(c)~(d)],整个重建过程与SENSE/GRAPPA的重建过程是一样的.在多层激发二维加速的情况下也是如此,加入相位方向的二倍欠采样后,多层激发二维加速图像的FOV变为参考图像的1/2,将两层参考图像拼接在一起并通过位置移动保持相位调制一致,构建一个五倍于二维加速图像FOV的没有混叠的扩展图像作为参考图像来计算k空间算子,填充k空间后则可解开混叠,如图 3所示.

|
图 3 CAIPIRINHA重建以及多层激发二维加速重建简化示意图.(a)经过相位调制同时激发两层时的混叠图像;(b) SENSE/GRAPPA重建的拼接图像和结果;(c)改进过的SENSE/GRAPPA算法,增加了一倍FOV;(d)为二维加速时的混叠图像和参考图像 Figure 3 The schematic diagram of CAIPIRINHA and multi-slice 2D acceleration reconstruction. (a) Simultaneously two-slice aliased image; (b) SENSE/GRAPPA reconstruction; (c) Adapted SENSE/GRAPPA reconstruction, add one FOV to concatenate image; (d) Multi-slice 2D acceleration reconstruction aliased image and reference image |
本文中的实验数据均使用上海联影医疗技术有限公司的1.5 T磁共振系统(uMR560)采集,分别进行了水模实验和人体实验,其中人体实验均征得志愿者知情并签订告知书.所有的参考图像都另行采集,不考虑参考图像的采集时间.图像重建均采用改进的SENSE/GRAPPA算法使用MATLAB进行离线重建.
1.2.1 水模实验本实验使用16通道头部线圈对一正方体分辨率水模进行扫描,使用基于CAIPIRINHA的BSSFP序列,分别进行了2组实验:(A)线性相位循环为(0,π)和(π/2,-π/2)情况下,CAIPIRINHA序列的相位循环比较实验;(B)多层激发二维加速成像方法与PPA四倍成像方法比较的加速方法比较试验.其中,多层激发二维加速成像中选层方向加速因子(MB factor)= 2、相位编码方向加速因子(Rpe)= 2、线性相位循环为(π/2,-π/2),而PPA四倍成像方法中沿相位编码方向加速因子Rpe= 4,其他实验参数如表 1所示.
| 表 1 水模实验和人体实验的部分实验参数 Table 1 Basic experimental parameters for phantoms and human subjects |
为了测试序列在人体上的可靠性和稳定性,本实验对8名男性志愿者(年龄分布在20~52岁之间)进行了扫描.实验设计如下:首先,使用24通道体线圈采集静态的多层激发二维加速心脏图像;然后,进行多层激发二维加速心脏电影图像的采集,MB factor = 2;Rpe = 2;覆盖全心共扫描8层,其它实验参数如表 1所示.电影图像采集时根据每名被试的心跳速度不同,分为17~24个期相,每个期相内包含12次相位编码,时间分辨率(time resolution)为40.8 ms,线性相位循环为(π/2,-π/2).实验中要求每名被试在扫描期间屏气,每次屏气之间有15~30 s的休息时间.
2 结果与讨论 2.1 水模实验结果从图 4中可以看到,基于BSSFP的相位调制多层激发序列在线性相位循环为(0,π)时,没有相位调制的一层产生了一个明显的圆环状带状伪影,线性相位循环为π的一层移动了FOV/2,且没有带状伪影;当线性相位循环为(π/2,-π/2)时,同时激发的两层都没有带状伪影,各向相反方向有FOV/4的位移,两层间的相对位移仍为FOV/2,且两层的信号强度相当.

|
图 4 两种线性相位循环情况下的相位调制多层激发图像. (a)相位循环为(0,π);(b)相位循环为(π/2,-π/2) Figure 4 Two RF phase encoding of CAIPIRINHA image. (a) (0, π) RF phase encoding image. (b) (π/2, -π/2) RF phase encoding image |
多层激发二维加速时混叠伪影进一步加重,重建图像如图 5(b)所示,PPA四倍图像如图 5(c)所示,可以看出由于叠加的射频脉冲同时激发了两层图像,相位调制同时多层激发并不会因相位编码数的减少导致采集到的信号强度减弱.从结果上看,PPA四倍成像方法更容易出现重建伪影,其图像质量劣于多层激发二维四倍加速.

|
图 5 不加速、多层激发二维加速与PPA四倍图像对比. (a)不加速图像;(b)二维加速重建图像;(c) PPA四倍图像 Figure 5 Comparison of images acquired using (a) Conventional non-accelerated technique; (b) Multi-slice 2D acceleration |
由于采用并行成像方法重建后,噪声不再是空间独立随机变量[14],我们根据NEMA2008标准[15, 16]的方法计算了SNR,如(8) 式所示,其中s1、s2分别表示同一片层的两次相同扫描图像.本实验针对三种不同的加速模式,分别从两个不同的片层组中选取了66个像素大小的感兴趣区(ROI)计算了信噪比,结果如表 2所示,可以看出,集成了多层激发技术图像的信噪比明显高于仅使用PPA技术的图像.
| $SNR = \frac{{mea{n_{ROI}}(s1 + s2)/2}}{{st{d_{ROI}}(s1 + s2)/\sqrt 2 }}$ | (8) |
其中,mean表示平均值,std表示标准差.
| 表 2 不同加速方式采集图像的信噪比(SNR) Table 2 SNR of images acquired with different acceleration method |
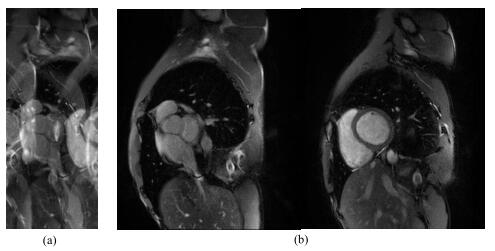
人体实验中进行了8层心脏扫描,其采集参数如表 1所示,选取其中一层静态图像的采集与重建结果如图 6所示.相位编码方向的欠采样导致除去欠采样的相位编码后相位方向的FOV变为原来的1/2.由于每层叠加不同的线性相位调制增大了空间灵敏度矩阵的变化,使其在图像重建时必为非奇异矩阵.改进后的SENSE/GRAPPA算法可以很好的对混叠图像进行重建,没有出现相位调制不一致导致的伪影.
|
图 6 (a)混叠图像;(b)本文提出的方法所获得的重建图像 Figure 6 (a) Aliased image using conventional method; (b) Images reconstructed using our proposed technique |
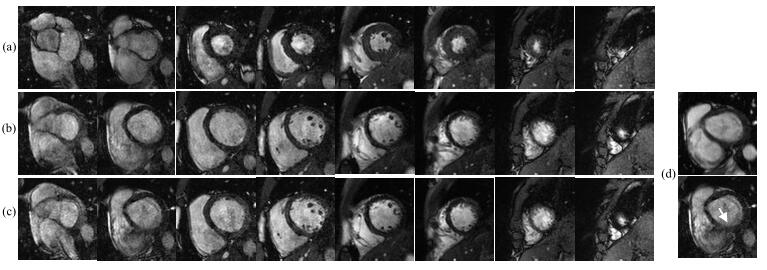
在心脏电影实验中由于图像数量过多,本文选取心动周期中最具代表性的3个期相,分别是心脏收缩末期、心脏舒张末期以及收缩末期到舒张末期中间期相进行展示.从图 7中可以看出,心脏的边界明显,且在最重要的收缩末期和舒张末期图像非常清晰,在血液流动大的层面的中间期相的图像会有一些搏动伪影,但不影响运动的观测以及心室容积的测量.第二层中间期相不加速与多层激发二维加速对比图如图 7(d)所示.
|
图 7 多层激发二维加速心脏电影实验结果图.(a)在心脏收缩末期的全心图像;(b)心脏舒张末期的全心图像;(c)收缩末期和舒张末期中间状态的全心图像;(d)第二层中间期相不加速与多层激发二维加速对比图,可明显看出箭头处有搏动伪影 Figure 7 Multi-slice 2D acceleration CINE. (a) End-systolic images; (b) Images between end-systolic and end-diastolic; (c) End-diastolic images; (d) Comparison between non-accelerated and accelerated images |
对于心脏电影实验,本文对同一被试的一组不加速、三组多层激发二维四倍加速数据进行了统计,计算了舒张末期容积、收缩末期容积、每搏输出量与射血分数,结果如表 3所示.同时本研究也对利用不加速和二维四倍加速方法采集的两组8名被试的心脏功能数据采用独立t检验进行了统计分析,结果如表 4所示,其p值分别为0.86、0.98、0.76和0.82,无显著差异,说明本文提出的多层激发二维四倍加速方法基本上不会影响心功能数据的计算.
| 表 3 不同加速采集时,同一被试心功能数据统计表 Table 3 Statistical table of one volunteer cardiac function data with different acceleration |
| 表 4 不加速和二维四倍加速采集时,8名被试的心功能数据统计 Table 4 Statistical analysis of all volunteer cardiac function data |
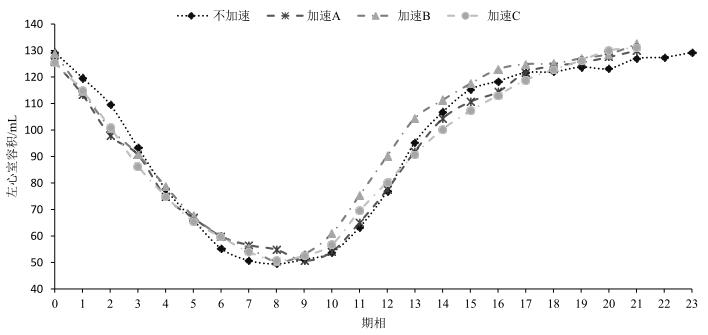
另外,我们还统计了同一被试的一组不加速、三组多层激发二维四倍加速方式采集时左心室容积变化(如图 8所示).由于心率有所差别,所以不加速的心脏电影图像的期相为24,而二维加速的心脏电影图像的期相为22.但是四组数据的趋势以及幅值非常接近,说明本文提出的多层激发二维四倍加速方法基本上不会影响心室的分割以及心脏跳动情况的观测.
|
图 8 左心室容积曲线 Figure 8 Left ventricular volume curve |
从以上结果中可以看到,多层激发二维四倍加速方法所获得的图像质量优于PPA四倍成像方法(图 5).在常规临床心脏电影成像的过程中,每层不加速的心脏电影图像扫描需14 s,8层心脏扫描需8次屏气,每两次屏气间需15~30 s的休息时间,因此整个过程需要4~6 min.长时间多次屏气对患者来说是一种负担,特殊患者甚至无法做到.当多层激发二维加速用于心脏电影成像时,8层心脏扫描的时间只需要30 s,分两次屏气即可完成,整个扫描过程只需45~60 s,当患者屏气时间小于10 s时也可增加屏气次数减少每次屏气所需的时间.并且多层激发二维加速心脏电影图像的重建参考图像只需要一组静态参考图像即可,进一步节省了数据采集时间.
但本方法仍有许多值得改进的地方:(1)本文目前做到的是同时激发两层相位编码方向上两倍加速,但若同时激发两层相位编码方向上三倍加速,可以利用2和3的循环差进行相位跳变,在相位编码时不需要做特殊的改动;也可以尝试在片层方向上增加加速倍数,而增加加速倍数会对重建算法提出更高的要求.(2)由于GRAPPA算法中k空间中的点与相邻点的线性关系在高倍加速情况下并不一定成立,也有科研人员[17]建议使用迭代等更高级的重建算法.(3)在心脏电影成像中,采用多倍加速成像方法比不加速成像方法的图像更容易出现搏动伪影,需要进一步尝试改进方法,未来可以尝试对运动不敏感的径向采集方式[18].
3 结论心脏电影成像技术虽然无创无害、功能强大,却因屏气扫描时间过长限制了其在临床上的应用.基于相位调制同时多层激发以及并行成像的二维加速技术在心脏电影成像上的运用,使得其在保障了图像质量的前提下缩短了扫描时间,提高了扫描效率,并可以对心脏功能进行准确测量.同时,这个技术降低了对患者屏气时间的要求,提升了检查的舒适度,有利于心脏电影成像技术在临床上的广泛应用.
| [1] | PENNELL D J, SECHTEM U P, HIGGINS C B, et al. Clinical indications for cardiovascular magnetic resonance (CMR):Consensus Panel report[J]. Eur Heart J, 2004, 25(21): 1940-1965. DOI: 10.1016/j.ehj.2004.06.040. |
| [2] | PETITJEAN C, DACHER J N. A review of segmentation methods in short axis cardiac MR images[J]. Med Image Anal, 2011, 15(2): 169-184. DOI: 10.1016/j.media.2010.12.004. |
| [3] | HEIDEMANN R M, ÖZSARLAK Ö, PARIZEL P M, et al. A brief review of parallel magnetic resonance imaging[J]. Eur Radiol, 2003, 13(10): 2323-2337. DOI: 10.1007/s00330-003-1992-7. |
| [4] | BREUER F A, BLAIMER M, HEIDEMANN R M, et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging[J]. Magn Reson Med, 2005, 53(3): 684-691. DOI: 10.1002/(ISSN)1522-2594. |
| [5] | BARTH M, BREUER F, KOOPMANS P J, et al. Simultaneous multislice (SMS) imaging techniques[J]. Magn Reson Med, 2016, 75(1): 63-81. DOI: 10.1002/mrm.25897. |
| [6] | OPPELT B A, GRAUMANN R, BARFUB H, et al. FISP:A new fast MRI sequence[J]. Electromedica, 1986, 54: 15-18. |
| [7] | WEBER O M, SPEIER P, SCHEFFLER K, et al. Assessment of magnetization transfer effects in myocardial tissue using balanced steady-state free precession (bSSFP) cine MRI[J]. Magn Reson Med, 2009, 62(3): 699-705. DOI: 10.1002/mrm.v62:3. |
| [8] | STÄB D, RITTER C O, BREUER F A, et al. CAIPIRINHA accelerated SSFP imaging[J]. Magn Reson Med, 2011, 65(1): 157-164. DOI: 10.1002/mrm.22600. |
| [9] | BLAIMER M, BREUER F A, SEIBERLICH N, et al. Accelerated volumetric MRI with a SENSE/GRAPPA combination[J]. J Magn Reson Imaging, 2006, 24(2): 444-450. DOI: 10.1002/(ISSN)1522-2586. |
| [10] | SOBOL W T, GAUNTT D M. On the stationary states in gradient echo imaging[J]. J Magn Reson Imaging, 1996, 6(2): 384-398. DOI: 10.1002/(ISSN)1522-2586. |
| [11] | PRUESSMANN K P, WEIGER M, SCHEIDEGGER B, et al. SENSE:sensitivity encoding for fast MRI[J]. Magn Reson Med, 1999, 42(5): 952-962. DOI: 10.1002/(ISSN)1522-2594. |
| [12] | GRISWOLD M A, JAKOB P M, HEIDEMANN R M, et al. Generalized autocalibrating partially parallel acqusitions(GRAPPA)[J]. Magn Reson Med, 2002, 47(6): 1202-1210. DOI: 10.1002/(ISSN)1522-2594. |
| [13] | SETSOMPOP K, GAGOSKI B A, POLIMENI J R, et al. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty[J]. Magn Reson Med, 2012, 67(5): 1210-1224. DOI: 10.1002/mrm.23097. |
| [14] | KELLMAN P, MCVEIGH E R. Image reconstruction in SNR units:A general method for SNR measurement[J]. Magn Reson Med, 2005, 54(6): 1439-1447. DOI: 10.1002/(ISSN)1522-2594. |
| [15] | NEMA. National Manufacturers Electrical Association standards (MS1-2008):determination of signal-to-noise ratio in diagnostic magnetic resonance imaging[R]. 2008. |
| [16] | DING Y, CHUNG Y C, SIMONETTI O P. A method to assess spatially variant noise in dynamic MR image series[J]. Magn Reson Med, 2010, 63(3): 782-789. DOI: 10.1002/mrm.v63:3. |
| [17] | OTAZO R, KIM D, AXEL L, et al. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI[J]. Magn Reson Med, 2010, 64(3): 767-776. DOI: 10.1002/mrm.v64:3. |
| [18] | YUTZY S R, SEIBERLICH N, DUERK J L, et al. Improvements in multislice parallel imaging using radial CAIPIRINHA[J]. Magn Reson Med, 2011, 65(6): 1630-1637. DOI: 10.1002/mrm.22752. |
 2017, Vol. 34
2017, Vol. 34 
