2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
固体核磁共振(NMR)技术在近十年来得以快速的发展,被广泛地用于膜蛋白的结构研究[1-15].
与可溶蛋白的微晶样品相比,重组至膜环境中膜蛋白的固体NMR实验的灵敏度较低.因此,需要更长的时间进行NMR信号累加,才能获得信噪比足够的NMR谱.同时,由于膜蛋白的一维13C或15N NMR谱信号堆叠非常严重,往往需要利用多个多维异核相关实验,例如NCACX、NCOCX、CONCA、CAN(CO)CX或CON(CA)CX,才能完成蛋白质的信号归属.在这些多维固体NMR实验中,双交叉极化(DCP)是最常用的建立13C-15N或15N-13C异核相关的实验技术,它的效率在很大程度上决定了固体NMR多维异核相关实验的效率.假如3D NCACX在DCP效率为50%时的实验时间是2天;但是如果DCP效率只有25%时,得到相同质量的谱的实验时间将会增加为8天.
DCP对实验条件非常敏感,例如13C和15N射频场的强度、射频场的调制幅度和交叉极化的接触时间等很多因素,都会影响DCP的实验效率.在实际实验中,为了寻找DCP的最佳实验条件,我们通常需要花费大量的时间去优化多个实验参数.尽管如此,样品或仪器的不稳定仍然会增加优化的难度,从而不能获得最佳的DCP实验效率[16-24].因此,分析影响DCP效率的主要因素,以指导DCP实验的优化,对于膜蛋白的固体NMR研究具有重要的意义.
对于膜蛋白样品,蛋白质分子整体或局部的运动将改变偶极耦合相互作用常数(D)或旋转坐标下的自旋-晶格弛豫时间(T1ρ),从而影响DCP效率.不同膜蛋白样品的DCP效率的差异源于其运动性的差异[13-15, 25-27].在2002年,Kolodziejski与Klinowski分析了不同研究对象的交叉极化(CP)动力学模型[28].在DCP技术中,其中最关键的15N-13C CP符合I-S模型.通过比较文献或实测的动力学参数偶极耦合常数(DNC)和T1ρ,利用(1) 式(见后文)可以定量地描述膜蛋白中动力学参数对DCP效率的影响.
为了研究影响膜蛋白样品DCP效率的主要因素,我们定量分析了3种膜蛋白样品的DCP效率与动力学参数(D和T1ρ)的关系.这3种样品分别是水通道蛋白(AQPZ)[29]、二酰脂甘油激酶(DAGK)[30-32]和与手足口病相关的肠道病毒孔道蛋白(EV71 2B)[33-35].在前期的工作中,我们发现这3种膜蛋白样品的DCP效率差别较大,能够很好地代表具有多种动力学特性的膜蛋白样品.基于动力学参数对DCP效率的影响的分析结果,我们可以在DCP实验前快速地测量相关动力学参数,预估未知样品的最佳DCP效率,为DCP实验条件的优化提供依据.
1 实验部分 1.1 膜蛋白样品DAGK脂质体样品的制备过程参照Chen等人[30]的文章.EV71 2B蛋白在大肠杆菌Rosetta(DE3)上表达,其纯化以及脂膜重建的流程与DAGK类似[30].AQPZ蛋白在大肠杆菌Bl21(DE3)上进行表达,并使用亲和色谱法纯化.将一定量的AQPZ蛋白与磷脂混合后,在18 ℃下轻摇孵育2 h,然后通过透析使AQPZ重组至磷脂膜中.最后,通过超速离心得到AQPZ脂质体样品.表 1列出了这3种膜蛋白样品的详细信息,包括蛋白质名称、同位素标记方式、磷脂种类、蛋白与磷脂质量比以及含水量(即水质量/脂质体干重)等.
| 表 1 3种膜蛋白样品的详细信息 Table 1 Details of three kinds of membrane protein samples |
所有的固体NMR实验都在固体宽腔Varian 600 MHz(14.1 T)谱仪上完成,使用3.2 mm T3-HXY MAS三共振探头.在CP/DCP实验中,AQPZ样品的转速(ωr)为8 kHz,DAGK和EV71 2B样品的转速为11.111 kHz[36].二维DIPSHIFT实验和T1ρ测量实验的转速分别是8 kHz和11.111 kHz.
13C NMR化学位移使用金刚烷定标(亚甲基碳化学位移:δC 40.5)[37].样品实验温度经硝酸铅温度校正,为274 K.
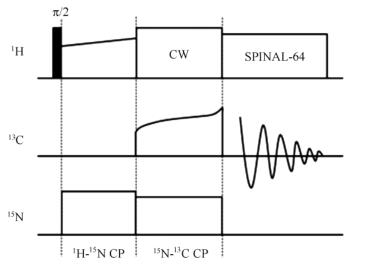
在CP实验中,1H-13C CP使用6.5ωr/6.5ωr的匹配条件.在DCP实验中(图 1),1H-15N CP使用6.5ωr/4.5ωr的匹配条件,15N-13C CP使用2.5ωr/1.5ωr的匹配条件.为了提高CP的效率和稳定性,我们采用了射频场的幅度调制[38].其中,1H-13C CP和1H-15N CP在1H通道上使用约±8%的1H线性幅度调制,15N-13C CP使用约±8%的13C正切幅度调制[39-41].在采样期间和15N-13C CP期间,1H通道分别使用约65 kHz的SPINAL-64去耦和90 kHz的CW去耦.
|
图 1 DCP实验的脉冲序列.1H-15N CP在1H通道上使用约±8%的1H线性幅度调制,15N-13C CP使用约±8%的13C正切幅度调制.在15N-13C CP和采样期间,1H通道分别使用约90 kHz的CW去耦和约65 kHz的SPINAL-64去耦 Figure 1 Pulse sequence diagram of DCP experiments. 1H-15N CP uses about ±8% linear amplitude modulation on 1H channel, and 15N-13C CP uses about ±8% tangent amplitude modulation on 13C channel. About 90 kHz CW proton decoupling power was applied during 15N-13C CP, and about 65 kHz SPINAL-64 power was applied during acquisition |
在二维DIPSHIFT实验中,异核偶极重耦使用R1817序列.T1ρ测量方法参考Cady等人[42]文章,1HNT1ρ测量的自旋锁场的有效场强分别为40 kHz与60 kHz,使用序列Lee-Goldburg(LG)spin-lock.
15N和13C核的T1ρ测量,基于CP后使用spin-lock序列,自旋锁场的有效场强均为50 kHz,设定15N NMR积分范围在δN 98~132,13CαNMR积分范围在δC 45~75,使用非线性方程最小二乘法通过matlab拟合得到单指数衰减曲线,所得数据的主要误差来源为积分区域内的噪声干扰[34, 43-46].
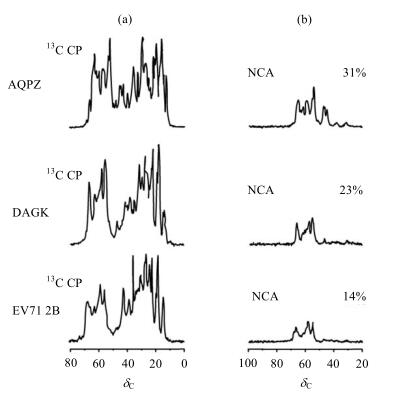
2 结果与讨论 2.1 不同膜蛋白样品DCP效率DCP的实验效率定义为η=S(NCA)/S(CP),其中,S(NCA)和S(CP)分别是NCA谱(即经过1H-15N CP与15N-13C CP得到主链的13Cα信号)和13C CP谱在δC45~70范围内的积分值[47].经过测量,AQPZ、DAGK和EV71 2B样品的DCP效率分别为31%、23%和14%(图 2).13C CP谱的积分区域(δC 45~70)包含Thr与Ser残基的Cβ信号,可能导致η的计算值略小于真实结果.但是,3种蛋白质样品中Thr和Ser残基的数目都小于残基总数的10%,因此理论上Thr和Ser残基的Cβ信号对实验结果的干扰小于10%.
|
图 2 AQPZ、DAGK和EV71 2B样品的(a) 1D 13C CP谱和(b) 1D 13C NCA谱.其中,EV71 2B样品的1D NCA谱的累加次数是256,其它谱的累加次数均为64.DCP的实验效率η=S(NCA)/S(CP),其中S是δC 45~70范围内的积分值 Figure 2 1D 13C CP (a) and 13C NCA (b) spectra of AQPZ, DAGK and EV71 2B samples. 256 scans were recorded for NCA spectra of EV71 2B and 64 scans were recorded for NCA spectra of others. DCP experimental efficiency η=S(NCA)/S(CP), where S is the integral of spectrum between δC 45~70 |
DCP的效率与15N-13C CP期间的质子去耦功率有关.当质子去耦的功率不足时,DCP效率将降低.我们在15N-13C CP期间分别使用了80 kHz、85 kHz和90 kHz 3种质子去耦功率,以观察去耦功率对DCP效率的影响.以AQPZ样品为例,80 kHz、85 kHz和90 kHz的质子去耦功率对应的DCP效率分别为29.3%、31.2%和31.3%.DAGK和EV71 2B样品的DCP效率存在类似的变化趋势.该实验结果表明:在当前的实验条件下(ωr = 8 kHz或11.111 kHz,以及1.5ωr/2.5ωr的13C-15N匹配条件),80~90 kHz的射频场基本能够满足DCP的去耦需求.更强的射频场提高DCP效率的作用有限,反而可能导致膜蛋白样品的发热变性.
已有的研究表明,微晶样品GB1和α-SH3的DCP(NCA)效率可以达到50%(500 MHz -3.2 mm MAS探头-11.111 kHz转速)[48, 49],而膜蛋白Proteorhodopsin的效率仅约30%(800 MHz -3.2 mm E-free探头-14.3 kHz转速)[25].尽管不同场强、探头以及装样方式对DCP效率都存在一定的影响,但是,综合对比多种蛋白质样品的DCP实验结果(膜蛋白AQPZ、DAGK、EV71 2B和Proteorhodopsin,微晶蛋白GB1和α-SH3),我们可以明显地看到:膜蛋白样品的DCP效率要低于可溶蛋白的微晶样品.这一结果可能源于蛋白质的运动性差异:膜蛋白在磷脂膜环境下通常比在微晶状态下的蛋白质多一些运动性.在CP动力学中,D和T1ρ是决定DCP效率的主要因素.而运动将削弱D或缩短T1ρ.因此,我们将定量分析D和T1ρ,以分析它们对膜蛋白样品DCP效率的影响.
2.2 偶极耦合相互作用常数测量蛋白质分子中相应残基的大幅度快速运动会削弱1H-13C、1H-15N和13C-15N偶极耦合相互作用.当运动足够快时,例如溶液中分子的快速翻滚会导致偶极耦合消失,从而使得我们无法获得基于偶极耦合的CP信号.在CP动力学公式,CP时间常数(TNC)与13C-15N偶极耦合直接相关.13C-15N偶极耦合的测量非常耗时.而运动会对13C-15N偶极耦合和1H-15N偶极耦合造成相似的影响.因此,我们可以通过测量1H-15N偶极耦合常数,以间接比较不同蛋白质样品的13C-15N偶极耦合常数.
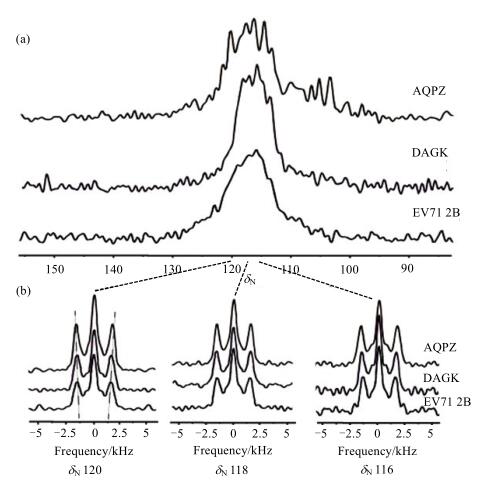
图 3是3种蛋白质在不同15N化学位移(δN 116、118、120)处的1H-15N偶极耦合线型.根据1H-15N偶极裂分和偶极重耦序列的缩窄因子(к)[50],我们可以得到1H-15N偶极耦合常数bHN(AQPZ)≈10.8 kHz、bHN(DAGK)≈10.5 kHz和bHN(EV71 2B)≈9.8 kHz.这3种样品的bHN大小关系与其DCP效率高低的对比一致.但是,较小的bHN差异并不能完全解释较大的DCP效率差异.例如,AQPZ的1H-15N偶极耦合比EV71 2B大10 %,而AQPZ的DCP效率却比EV71 2B高了120 %.因此,对于这3种蛋白样品的DCP效率的差异,偶极耦合的贡献较小,T1ρ可能是更重要的影响因素.
|
图 3 (a) AQPZ, DAGK, EV71 2B样品的1D 15N CP谱;(b) 3种蛋白质在不同15N化学位移(δN116、118、120)处的1H-15N偶极耦合线型.虚线表示了偶极裂分的趋势 Figure 3 (a) 1D 15N CP spectra of AQPZ, DAGK and EV71 2B; (b)1H-15N dipolar coupling line shapes from left to right were extracted from three resonances at δN 120、118 and 116 of 2D DIPSHIFT spectra in different samples. Dashed lines around split peaks were drawn to indicate the tendency of dipolar splittings |
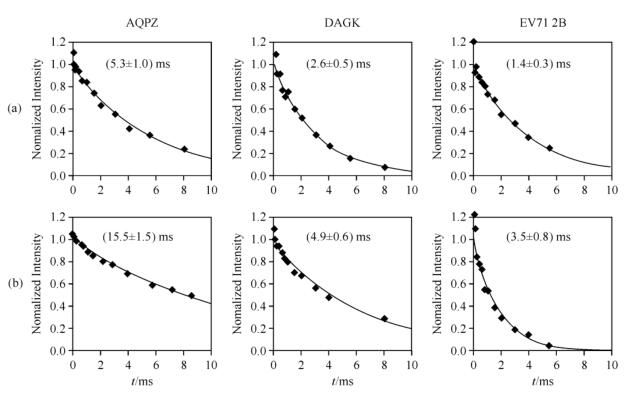
T1ρ与样品运动性密切相关.当运动的时间尺度接近微秒(μs)时,运动将明显缩短T1ρ.在中等转速下,固体NMR通常利用T1ρH来的表征蛋白质的运动性.在40 kHz的自旋锁场场强下,AQPZ、DAGK和EV71 2B的T1ρ(1HN)分别为(5.3±1.0)ms、(2.6±0.5)ms和(1.4±0.3)ms(图 4).在更强的射频场(60 kHz)下,它们的T1ρ(1HN)均有所增加(图 4),但对比关系依然是T1ρ(1HN)(AQPZ) > T1ρ(1HN)(DAGK) > T1ρ(1HN)(EV71 2B).这与DCP效率的对比关系一致,说明运动导致的T1ρ缩短可能是DCP效率降低的原因.但是,T1ρ(1HN)仅表征样品运动性,并不是影响15N-13C CP的直接因素,因此我们进一步测量了T1ρC和T1ρN以定量分析它们对DCP效率的贡献.图 5是测量T1ρC(a)和T1ρN(b)的实验数据和相应的拟合结果.在相同的锁场射频场强下,3种蛋白质样品的T1ρC和T1ρN对比关系与T1ρ(1HN)一致,即T1ρC/N(AQPZ) > T1ρC/N(DAGK) > T1ρC/N(EV71 2B).
|
图 4 自旋锁场的有效场强分别为40 kHz (a)与60 kHz (b)时的信号拟合得到AQPZ、DAGK、EV71 2B的T1ρ(1HN)时间的拟合曲线 Figure 4 T1ρ(1HN) decay curves of AQPZ, DAGK and EV71 2B. Effective spin-lock fields are 40 kHz (a) and 60 kHz (b) |
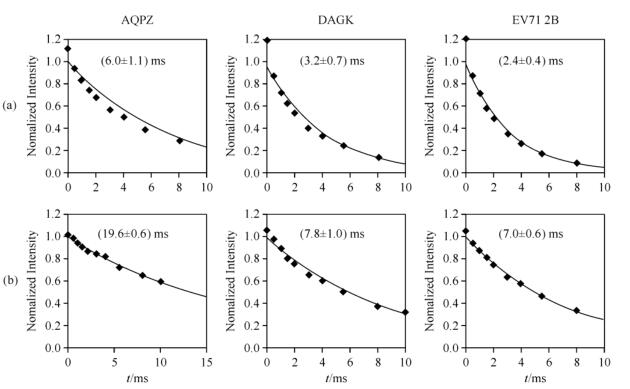
|
图 5 自旋锁场的有效场强为50 kHz时的得到的弛豫信号拟合得到不同样品对于T1ρN(a)与T1ρC(b)衰变曲线,具体细节与图 4相同 Figure 5 T1ρN (a) and T1ρC (b) decay curves of the 3 samples (effective spin-lock fields is 50 kHz). Details are same as Fig. 4 |
为了定量分析T1ρ与η的关系,我们建立了DCP动力学模型.15N-13C CP参考经典I-S模型[28],建立动力学公式为:
| $\eta = \frac{{I(t)}}{{I(0)}} = {(1 + \frac{{{T_{{\rm{NC}}}}}}{{T_{1\rho }^{\rm{C}}}} - \frac{{{T_{{\rm{NC}}}}}}{{T_{1\rho }^{\rm{N}}}})^{ - 1}}\left\{ {\exp ( - \frac{t}{{T_{1\rho }^{\rm{N}}}}) - \exp [ - t(\frac{1}{{{T_{{\rm{NC}}}}}} + \frac{1}{{T_{1\rho }^{\rm{C}}}})]} \right\}$ | (1) |
其中,TNC是CP时间常数.它的倒数1/TNC是CP速率常数,与偶极相互作用常数bNC呈正相关.由于不同样品的bHN变化小于10%,我们可以近似地认为TNC不变.根据膜蛋白M2的实验数据[51],我们将TNC设为4 ms.根据(1) 式,我们计算了不同T1ρC和T1ρN的CP的最大效率(图 6).图 6标出了根据T1ρC和T1ρN实验值得到的DCP理论效率.3种样品的DCP理论效率与实验效率基本吻合,因此通过我们的动力学模型可以根据T1ρ值有效地定量预测样品DCP理论效率.

|
图 6 随T1ρC和T1ρN变化DCP效率的变化图.根据(1) 式对CP动力学参数T1ρC和T1ρN进行模拟得到DCP效率的等高线,15N-13C CP参考经典I-S模型, 等高线代表归一化后随着T1ρC和T1ρN变化时,对应15N-13C CP的传递效率的变化.3个坐标表示3种样品的DCP理论效率 Figure 6 Contour curve of DCP efficiency of T1ρCand T1ρN in Eq. (1). The 15N-13C CP is referred to the classical I-S model. And the curve value is the normalized 15N-13C CP efficiency to T1ρCand T1ρN. Three coordinates express DCP efficiencies of three of samples in theory |
基于以上分析结果,我们可以根据T1ρ值预先定量预测某个样品的最佳DCP效率,并以此作为DCP实验的优化目标.这可以避免盲目的大范围搜寻15N-13C CP匹配条件,从而节省用于优化DCP实验的时间.
3 结论我们分析了3种典型的在膜环境中膜蛋白样品(AQPZ、DAGK和EV71 2B)的DCP效率及其影响因素.在相同的实验条件下,3种蛋白样品的DCP效率存在明显差异,其中,AQPZ的DCP效率最高(31%),DAGK的效率次之(23%),EV71 2B的效率最低(14%).我们测量了T1ρ和D,发现在这3种样品中膜蛋白的运动会明显缩短T1ρ,而对D的影响相对较小.基于CP动力学的分析,我们证实了运动导致的T1ρ缩短是降低DCP效率的主要原因,并建立了T1ρ与DCP效率的模型进行定量分析.因此,在研究一个全新的膜蛋白样品时,在DCP实验前分析相应的T1ρ数据,我们可以预估其DCP的最佳效率,从而为之后的DCP实验优化提供依据.
| [1] | SCHOLZ I, HUBER M, MANOLIKAS T, et al. MIRROR recoupling and its application to spin diffusion under fast magic-angle spinning[J]. Chem Phys Lett, 2008, 460(1): 278-283. |
| [2] | DE PAËPE G, LEWANDOWSKI J R, LOQUET A, et al. Proton assisted recoupling and protein structure determination[J]. J Chem Phys, 2008, 129(24): 245101-245122. DOI: 10.1063/1.3036928. |
| [3] | LEWANDOWSKI J R, DE PAËPE G, GRIFFIN R G. Proton assisted insensitive nuclei cross polarization[J]. J Am Chem Soc, 2007, 129(4): 728-729. DOI: 10.1021/ja0650394. |
| [4] | MORCOMBE C R, GAPONENKO V, BYRD R A, et al. Diluting abundant spins by isotope edited radio frequency field assisted diffusion[J]. J Am Chem Soc, 2004, 126(23): 7196-7197. DOI: 10.1021/ja047919t. |
| [5] | BALDUS M, PETKOVA A T, HERZFELD J, et al. Cross polarization in the tilted frame:assignment and spectral simplification in heteronuclear spin systems[J]. Mol Phys, 1998, 95(6): 1197-1207. DOI: 10.1080/00268979809483251. |
| [6] | PINES A, GIBBY M, WAUGH J. Proton-enhanced nuclear induction spectroscopy. A method for high-resolution NMR of dilute spins in solid[J]. J Chem Phys, 1972, 56(4): 1776-1777. DOI: 10.1063/1.1677439. |
| [7] | TAKEGOSHI K, NAKAMURA S, TERAO T. 13C-1H dipolar-assisted rotational resonance in magic-angle spinning NMR[J]. Chem Phys Lett, 2001, 344(5): 631-637. |
| [8] | BJERRING M, NIELSEN N C. Solid-state NMR heteronuclear coherence transfer using phase and amplitude modulated rf irradiation at the Hartmann-Hahn sideband conditions[J]. Chem Phys Lett, 2003, 382(5): 671-678. |
| [9] | BIELECKI A, BURUM D P. Temperature dependence of 207Pb MAS spectra of solid lead nitrate. An accurate, sensitive thermometer for variable-temperature MAS[J]. J Magn Reson, Ser A, 1995, 116(2): 215-220. DOI: 10.1006/jmra.1995.0010. |
| [10] | MILDNER T, ERNST H, FREUDE D. 207Pb NMR detection of spinning-induced temperature gradients in MAS rotors[J]. Solid State Nucl Magn Reson, 1995, 5(3): 269-271. DOI: 10.1016/0926-2040(95)01189-1. |
| [11] | HU B, AMOUREUX J P, TRÉBOSC J, et al. Through-space MP-CPMAS experiments between spin-1/2 and half-integer quadrupolar nuclei in solid-state NMR[J]. J Magn Reson, 2008, 192(1): 8-16. DOI: 10.1016/j.jmr.2008.01.008. |
| [12] | HEDIGER S, MEIER B, ERNST R. Cross polarization under fast magic angle sample spinning using amplitude-modulated spin-lock sequences[J]. Chem Phys Lett, 1993, 213(5, 6): 627-635. |
| [13] | MCDERMOTT A. Structure and dynamics of membrane proteins by magic angle spinning solid-state NMR[J]. Annu Rev Biophys, 2009, 38: 385-403. DOI: 10.1146/annurev.biophys.050708.133719. |
| [14] | GOOD D B, WANG S, WARD M E, et al. Conformational dynamics of a seven transmembrane helical protein anabaena sensory rhodopsin probed by solid-state NMR[J]. J Am Chem Soc, 2014, 136(7): 2833-2842. DOI: 10.1021/ja411633w. |
| [15] | PARK S H, CASAGRANDE F, DAS B B, et al. Local and global dynamics of the G protein-coupled receptor CXCR1[J]. Biochemistry, 2011, 50(12): 2371-2380. DOI: 10.1021/bi101568j. |
| [16] | JAIN S, BJERRING M, NIELSEN N C. Efficient and robust heteronuclear cross-polarization for high-speed-spinning biological solid-state NMR spectroscopy[J]. J Phys Chem Lett, 2012, 3(6): 703-708. DOI: 10.1021/jz3000905. |
| [17] | LAAGE S, MARCHETTI A, SEIN J, et al. Band-selective 1H-13C cross-polarization in fast magic angle spinning solid-state NMR spectroscopy[J]. J Am Chem Soc, 2008, 130(51): 17216-17217. DOI: 10.1021/ja805926d. |
| [18] | KEHLET C, BJERRING M, SIVERTSEN A C, et al. Optimal control based NCO and NCA experiments for spectral assignment in biological solid-state NMR spectroscopy[J]. J Magn Reson, 2007, 188(2): 216-230. DOI: 10.1016/j.jmr.2007.06.011. |
| [19] | HANSEN J Ø, KEHLET C, BJERRING M, et al. Optimal control based design of composite dipolar recoupling experiments by analogy to single-spin inversion pulses[J]. Chem Phys Lett, 2007, 447(1): 154-161. |
| [20] | BJERRING M, RASMUSSEN J T, KROGSHAVE R S, et al. Heteronuclear coherence transfer in solid-state nuclear magnetic resonance using a γ-encoded transferred echo experiment[J]. J Chem Phys, 2003, 119(17): 8916-8926. DOI: 10.1063/1.1613933. |
| [21] | RAYA J, HIRSCHINGER J. Application of rotor-synchronized amplitude-modulated cross-polarization in a 13C-1H spin pair under fast magic-angle spinning[J]. J Magn Reson, 1998, 133(2): 341-351. DOI: 10.1006/jmre.1998.1488. |
| [22] | YANG J, PARKANZKY P D, BODNER M L, et al. Application of REDOR subtraction for filtered MAS observation of labeled backbone carbons of membrane-bound fusion peptides[J]. J Magn Reson, 2002, 159(2): 101-110. DOI: 10.1016/S1090-7807(02)00033-2. |
| [23] |
TANG X Q, ZHANG Z F, YANG J. Heating of biological samples in studies of MAS solid-state NMR[J].
Chinese J Magn Reson, 2015, 32(1): 123-40.
唐新启, 张正逢, 杨俊. 生物固体核磁共振中样品发热的研究进展[J]. 波谱学杂志, 2015, 32(1): 123-40. DOI: 10.11938/cjmr20150114. |
| [24] |
LI H. High-pressure NMR for studying protein structure and dynamics[J].
Chinese J Magn Reson, 2016, 33(1): 1-26.
李华. 高压NMR在蛋白质结构和动力学研究中的应用[J]. 波谱学杂志, 2016, 33(1): 1-26. DOI: 10.11938/cjmr20160101. |
| [25] | SHI L C, AHMED M A M, ZHANG W R, et al. Three-dimensional solid-state NMR study of a seven-helical integral membrane proton pump-structural insights[J]. J Mol Biol, 2009, 386(4): 1078-1093. DOI: 10.1016/j.jmb.2009.01.011. |
| [26] | FRERICKS H L, ZHOU D H, YAP L L, et al. Magic-angle spinning solid-state NMR of a 144 kDa membrane protein complex:E. coli cytochrome bo3 oxidase[J]. J Bimol NMR, 2006, 36(1): 55-71. DOI: 10.1007/s10858-006-9070-5. |
| [27] | CASTELLANI F, VAN ROSSUM B, DIEHL A, et al. Structure of a protein determined by solid-state magic-angle-spinning NMR spectroscopy[J]. Nature, 2002, 420(6911): 98-102. DOI: 10.1038/nature01070. |
| [28] | KOLODZIEJSKI W, KLINOWSKI J. Kinetics of cross-polarization in solid-state NMR:a guide for chemists[J]. Chem Rev, 2002, 102(3): 613-628. DOI: 10.1021/cr000060n. |
| [29] | BORGNIA M J, KOZONO D, CALAMITA G, et al. Functional reconstitution and characterization of AqpZ, the E. coli water channel protein[J]. J Mol Biol, 1999, 291(5): 1169-1179. DOI: 10.1006/jmbi.1999.3032. |
| [30] | CHEN Y K, ZHANG Z F, TANG X Q, et al. Conformation and topology of diacylglycerol kinase in E. coli membranes revealed by solid-state NMR spectroscopy[J]. Angew Chem Int Ed, 2014, 53(22): 5624-5628. DOI: 10.1002/anie.v53.22. |
| [31] | VAN HORN W D, SANDERS C R. Prokaryotic diacylglycerol kinase and undecaprenol kinase[J]. Annu Rev Biophys, 2012, 41: 81-82. DOI: 10.1146/annurev-biophys-050511-102330. |
| [32] | VAN HORN W D, KIM H J, ELLIS C D, et al. Solution nuclear magnetic resonance structure of membrane-integral diacylglycerol kinase[J]. Science, 2009, 324(5935): 1726-1729. DOI: 10.1126/science.1171716. |
| [33] | NIU Z, ZHAO W J, ZHANG Z F, et al. The molecular structure of alzheimer β-amyloid fibrils formed in the presence of phospholipid vesicles[J]. Angew Chem Int Ed, 2014, 53(35): 9294-9297. DOI: 10.1002/anie.201311106. |
| [34] | ZHANG Z F, CHEN Y K, TANG X Q, et al. Solid-state NMR shows that dynamically different domains of membrane proteins have different hydration dependence[J]. J Phys Chem B, 2014, 118(32): 9553-9564. DOI: 10.1021/jp503032h. |
| [35] | XIE S Q, WANG K, YU W J, et al. DIDS blocks a chloride-dependent current that is mediated by the 2B protein of enterovirus 71[J]. Cell Res, 2011, 21(8): 1271-1275. DOI: 10.1038/cr.2011.112. |
| [36] | RALEIGH D, LEVITT M, GRIFFIN R. Rotational resonance in solid state NMR[J]. Chem Phys Lett, 1988, 146(1): 71-6. |
| [37] | MORCOMBE C R, ZILM K W. Chemical shift referencing in MAS solid state NMR[J]. J Magn Reson, 2003, 162(2): 479-486. DOI: 10.1016/S1090-7807(03)00082-X. |
| [38] | D'ESPINOSE DE LACAILLERIE J B, BARBERON F, ROMANENKO K V, et al. 95Mo magic angle spinning NMR at high field:improved measurements and structural analysis of the quadrupole interaction in monomolybdates and isopolymolybdates[J]. J Phys Chem B, 2005, 109(29): 14033-14042. DOI: 10.1021/jp0519621. |
| [39] | METZ G, WU X L, SMITH S O. Ramped-amplitude cross polarization in magic-angle-spinning NMR[J]. J Magn Reson, Ser A, 1994, 110(2): 219-227. DOI: 10.1006/jmra.1994.1208. |
| [40] | HEDIGER S, MEIER B, ERNST R. Adiabatic passage Hartmann-Hahn cross polarization in NMR under magic angle sample spinning[J]. Chem Phys Lett, 1995, 240(5): 449-456. |
| [41] | LOENING N M, BJERRING M, NIELSEN N C, et al. A comparison of NCO and NCA transfer methods for biological solid-state NMR spectroscopy[J]. J Magn Reson, 2012, 214: 81-90. DOI: 10.1016/j.jmr.2011.10.012. |
| [42] | CADY S D, HONG M. Effects of amantadine on the dynamics of membrane-bound influenza A M2 transmembrane peptide studied by NMR relaxation[J]. J Bimol NMR, 2009, 45. |
| [43] | HUSTER D, XIAO L S, HONG M. Solid-state NMR investigation of the dynamics of the soluble and membrane-bound colicin Ia channel-forming domain[J]. Biochemistry, 2001, 40(25): 7662-7674. DOI: 10.1021/bi0027231. |
| [44] | LINSER R, BARDIAUX B, ANDREAS L B, et al. Solid-state NMR structure determination from diagonal-compensated, sparsely nonuniform-sampled 4D proton-proton restraints[J]. J Am Chem Soc, 2014, 136(31): 11002-110010. DOI: 10.1021/ja504603g. |
| [45] | QUINN C M, MCDERMOTT A E. Monitoring conformational dynamics with solid-state R 1ρ experiments[J]. J Bimol NMR, 2009, 45. |
| [46] | QUINN C M, MCDERMOTT A E. Quantifying conformational dynamics using solid-state R 1ρ experiments[J]. J Magn Reson, 2012, 222: 1-7. DOI: 10.1016/j.jmr.2012.05.014. |
| [47] | FRANKS W T, KLOEPPER K D, WYLIE B J, et al. Four-dimensional heteronuclear correlation experiments for chemical shift assignment of solid proteins[J]. J Bimol NMR, 2007, 39(2): 107-131. DOI: 10.1007/s10858-007-9179-1. |
| [48] | FRANKS W T, ZHOU D H, WYLIE B J, et al. Magic-angle spinning solid-state NMR spectroscopy of the β1 immunoglobulin binding domain of protein G (GB1):15N and 13C chemical shift assignments and conformational analysis[J]. J Am Chem Soc, 2005, 127(35): 12291-12305. DOI: 10.1021/ja044497e. |
| [49] | FRANKS W T. Biomolecular solid-state nuclear magnetic resonance methods for spectral assignment and high-resolution structure determination of proteins[M]. Urbana: Butterworths, 2007. |
| [50] | ZHAO X, EDÉN M, LEVITT M H. Recoupling of heteronuclear dipolar interactions in solid-state NMR using symmetry-based pulse sequences[J]. Chem Phys Lett, 2001, 342(3): 353-361. |
| [51] | FU R Q, HU J, CROSS T A. Towards quantitative measurements in solid-state CPMAS NMR:A Lee-Goldburg frequency modulated cross-polarization scheme[J]. J Magn Reson, 2004, 168(1): 8-17. DOI: 10.1016/j.jmr.2004.01.012. |
 2017, Vol. 34
2017, Vol. 34 
