2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
核磁共振(Nuclear Magnetic Resonance, NMR)现象从1944年被发现以来,逐渐成为生物、化学、物理学、医学等领域必不可少的研究工具[1-3].基于磁共振原理的磁共振成像(Magnetic Resonance Imaging, MRI)技术[4],因具有检查手段灵活、可提供组织信息、对人体组织特性十分敏感、无放射性等优势,常用于功能成像和疾病检测.至今,与磁共振相关的诺贝尔奖已经多达5次,充分说明了这一技术的重要性.
尽管磁共振技术的优势十分明显,但是一直面临一个很大问题,即灵敏度低.灵敏度与核极化度(P)成正比,核极化度为:
| $ P = \frac{{{n_\alpha } - {n_\beta }}}{{{n_\alpha } + {n_\beta }}} $ | (1) |
原子核系综中,nα和nβ分别代表核自旋向上(ms= 1/2)和自旋向下(ms= -1/2),分布如图 1所示.

|
图 1 自旋极化的分布 Figure 1 Distribution of spin polarization |
在热平衡态,核极化度为:
| $ {P_0} = \tan {\rm{h}}\left( {\frac{{\gamma \hbar {B_0}}}{{2{\kappa _{\rm{B}}}T}}} \right) $ | (2) |
其中γ是核的旋磁比,B0是外磁场的强度,T是温度,κB是玻尔兹曼常数.以1H核为例,说明热平衡时的极化度[5].在磁场强度为18.8 T、温度为300 K的实验条件下,质子热力学极化度仅为P0≈ 9.6×10-4.这个缺陷严重制约了磁共振技术的发展.通过提高磁场强度、利用超低温探头等物理方法,虽然可以提高灵敏度,但是基于热力学平衡态的NMR检测,灵敏度依然达不到更高的要求.
如何让核自旋极化的水平远大于热平衡分布时的水平,一直是磁共振领域的热门研究课题.目前已经发展了多种超极化方法,如自旋交换光抽运(Spin-Exchange Optical Pumping,SEOP)[6, 7]、仲氢诱导核极化(Para-Hydrogen Induced Polarization,PHIP)[8]和化学诱导动态核极化(Chemically Induced Dynamic Nuclear Polarization, CIDNP)[9].
1953年,Overhauser[10]提出动态核极化(Dynamic Nuclear Polarization,DNP)理论[在NMR领域,更为广知的是核Overhauser效应(Nuclear Overhauser Effect, NOE)].60多年来,DNP已经发展了多种技术,如固态高场DNP[11]、变场DNP[12, 13]、溶解DNP[14, 15]、发展新的自由基[16]等.这些DNP方法基于微波驱动未成对电子,将热平衡态的电子极化转移到原子核,使核的极化增强.这种方法的DNP技术在我国也有发展[17-20].
是否可以先增加电子的极化度,再经过动态核极化将电子极化转移给原子核,来突破传统DNP的质子极化增强660倍的极限?这就是本文介绍的微波诱导光学核极化(Microwave Induced Optical Nuclear Polarization, MIONP).先简要介绍MIONP发展历史.1967年,Maier等人[21]发现了光学核极化(Optical Nuclear Polarization,ONP).Kastler证明了电子极化(Dynamic Electron Polarization,DEP或Optical Electronic Polarization,OEP)的可能性,并且考虑将电子的极化转移给核.ONP实验首先在重金属蒸汽(Hg和Cd)和惰性气体[22]中实现.随后实验上实现了分子晶体[21]、无机离子固体[23]和半导体[24]等固体中的ONP效应.1980年,ONP的一个重要分支——MIONP被发现是一种高效提高灵敏度的方法[25],相比自由基DNP,MIONP技术在1990年就已经突破了质子极化增强660倍的极限[26],并且有以下优势:(1)三重态的裂分不受温度和磁场影响,一些光激发分子内,处于亚稳态的光激发三重态的电子自旋极化率,远大于热平衡态的自由电子极化率[27];(2)由于三重态电子的寿命很短(大约几十个微秒)[28, 29],核的弛豫不受电子顺磁作用的影响,而在自由基DNP中,电子顺磁作用会加快原子核的弛豫并且导致退相干,降低极化转移效率[30].
目前MIONP研究的对象大多集中于晶体分子,如单晶或多晶样品中的质子,因此在介绍原理时以质子做为极化增强核.本文首先介绍MIONP的物理原理,然后结合最新的实验进展对实验条件进行详细的阐述,最后对MIONP的发展和研究状况做出总结和展望.
1 MIONP原理简介由于激光的激发频率与原子核的跃迁频率相差多个量级,光不能直接极化核,光激发方法必须利用电子作为中介.MIONP包含3个进程[31]:(1)激光照射三重态分子,激发电子从基态跃迁到第一激发态,再通过自旋-轨道偶合,单重态的电子跃迁到三重态,实现电子的极化;(2)通过电子-核超精细偶合,将电子极化转移到临近的原子核[26];(3)通过自旋扩散,逐渐增加基态核系综的磁化矢量[32].
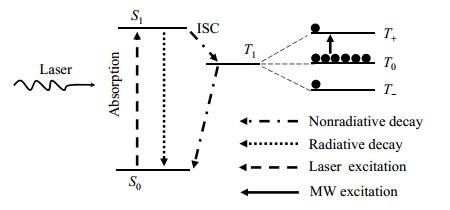
1.1 光学电子极化MIONP实验第一步必须实现光学电子极化.OEP不仅可以用于MIONP,也可以用于光检测磁共振(Optically Detected Magnetic Resonance, ODMR)[33].首先激光照射到晶体电子发生跃迁,由基态跃迁到第一激发态(S0→S1)(图 2)[31].通过自旋-轨道偶合作用,一部分激发态电子通过系间窜跃(InterSystem Crossing, ISC),转移到三重态T1(S1→T1),实现电子极化.
|
图 2 电子通过系间窜跃跃迁到三重态能级图{据文献[28]修改} Figure 2 Energy levels of a molecule photoexcitable to the triplet state via intersystem crossing{modified on the basis of ref. [28]} |
自旋系统包括三重态电子(S = 1)和一个1H核(I = 1/2),系统哈密顿量为[34]:
| $ H = {H_{ZFS}} + g\beta \overrightarrow S \cdot \overrightarrow {{B_0}} + {g_n}{\beta _n}\overrightarrow I \cdot \overrightarrow {{B_0}} + \overrightarrow S \cdot A \cdot \overrightarrow I $ | (3) |
| $ {H_{ZFS}} = D\left( {S_Z^2 - \frac{{{S^2}}}{3}} \right) + E\left( {S_X^2 - S_Y^2} \right) $ | (4) |
三重态上两个电子的偶极-偶极相互作用,形成零场分裂项HZFS,D和E是由于电子偶极-偶极相互作用的零场分裂参数;(3) 式第2项和第3项分别是电子和核的Zeeman分裂项,β和βn分别是电子和核的Bohr磁矩,g和gn分别是电子和核的g因子,最后一项是电子与核的超精细偶合项.不同的场强下,匹配的微波频率会引起电子自旋三重态mS=1↔mS=0或mS=-1↔mS=0之间的跃迁.如果没有三重态存在,两个跃迁会抵消.零场分裂的能级为千兆赫兹(GHz)量级,而光激发基态的跃迁为太赫兹(THz)量级.
由于自旋-轨道偶合,电子从高度极化的单态通过ISC跃迁到三重态,但是转移到三重态3个子能级的概率不是均等的.以并五苯分子为例,经过ISC过程后,其3个子能级mS= 1、0、-1的布居数分别为为0.12、0.76、0.12[29],使得三重态电子的极化度远大于热平衡时自由电子极化度,而且与温度和场强大小无关.当三重态极化建立之后,两个子能级间的布居数Pe(t)差与时间有关[36]:
| $ {P_e}\left( t \right) = \frac{{N\exp \left( { - kt} \right) - N'\exp \left( { - k't} \right)}}{{N\exp \left( { - kt} \right) + N'\exp \left( { - k't} \right)}} $ | (5) |
N和N'分别是三重态中两个能级上的布居数,k和k'是对应的衰减速率.
1.2 三重态电子与核的超精细偶合电子与核之间的偶合称为超精细偶合.相对于原子核间的J偶合、偶极偶合和化学屏蔽等作用,超精细偶合的量级很大,因此在MIONP过程中核间的相互作用可以忽略.超精细偶合包含各向同性和各向异性作用.各向同性的超精细偶合,也称为接触相互作用,是由原子核所在位置处不为0的电子波函数概率密度引起的.各向异性的超精细偶合,是由电子和原子核的偶极相互作用引起的.
对于芳香烃类有机分子,只有当电子自旋和核自旋相邻时,才存在各向同性作用.但是每一对电子-核自旋之间均存在偶极相互作用.电子自旋与其周围核自旋的偶极偶合强度正比于电子的自旋密度[37].
1.3 核的极化在激发三重态的有限存在时间里,极化后的电子和周围原子核间的超精细偶合作用使电子极化能够转移至核.这一过程类似于DNP过程,差别在于DNP将处于热平衡态的电子极化转移给核,而MIONP将处于非热平衡态的电子极化转移给核.MIONP首次实验是利用类似固态效应(Solid Effect,SE)的理论,来解释三重态电子极化向质子极化转移的过程[25].通过用微波连续照射样品分子,自旋系统间发生禁戒跃迁:△mS=±1,△mI=±1,近似于固态效应.但是这种禁戒跃迁实现的前提是三重态的零场分裂.后来Henstra等人[26]将绝热快速通过(adiabatic fast passages)方法应用到极化转移中,提出了完整固态效应(Integrated Solid Effect, ISE),在0.35 T场强和室温条件下利用萘参杂并五苯样品,观察到质子极化增强了5 500倍.
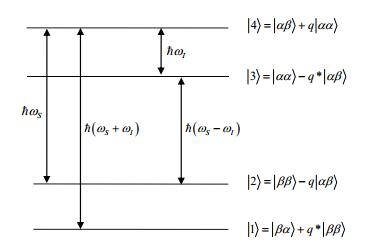
1.3.1 固态效应固态效应是两自旋效应,包含1个电子和1个核自旋系统.用微波照射系统,导致电子和核同时发生flip-flop,从而使电子的极化转移到与之偶合的核.由于电子-核之间的超精细偶合,系统哈密顿量包含非久期项,其本征态为混态,构成的四能级系统如图 3所示.在|αβ>态中,电子自旋在前,核自旋在后.|α>和|β>分别代表单自旋向上和单自旋向下态,q代表混合的程度.
|
图 3 固态效应的能级结构图 Figure 3 Energy levels of solid effect |
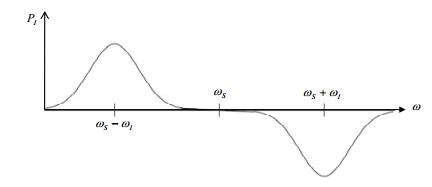
利用频率为ω=ωS±ωI的微波照射电子-核系统,饱和禁戒跃迁.当微波照射频率为ω=ωS+ωI时,饱和能级的布居数相等.由于电子的纵向弛豫时间远小于核的纵向弛豫时间,因此在微波照射的同时,电子从态|4>不断的跃迁到态|2>.最终导致|2>的布居数远大于|1>的布居数,使核的极化负增强.当微波照射频率为ω=ωS-ωI时,结果相反,如图 4所示.
|
图 4 核的极化度与微波频率的关系{来自文献[38]} Figure 4 Nuclear polarization versus microwave frequency{from ref. [38]} |
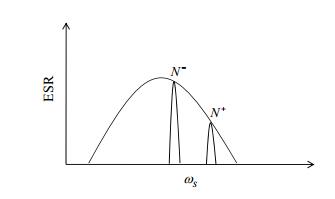
但是高场条件在固态效应中十分重要,必须要满足电子顺磁共振(Electron Spin Resonance, ESR)谱宽≤核的频率,才能保证频率为ω=ωS±ωI的微波照射时,电子极化高效地转移给核自旋[28].在低场时,电子的谱宽大于核频率,这种情况下电子谱宽会非均匀加宽.MIONP中三重态电子的两个ESR谱,由于超精细相互作用也会非均匀加宽,导致电子的谱宽大于核的频率.此时ESR谱可以看做由不同频率为ωSi、相互独立、均匀加宽的多个自旋包(spin packet)构成,每个自旋包的ESR谱宽度都小于核的频率.如图 5所示,N+和N-分别表示在各自自旋包位置ωSi处参与极化转移过程的电子数.电子自旋密度越大,ESR谱强度越大.横轴表示微波照射下的共振频率,纵轴表示ESR谱的强度.
|
图 5 电子自旋密度与微波频率关系{来自文献[26]} Figure 5 Density of electron spins versus the microwave frequency{from ref. [26]} |
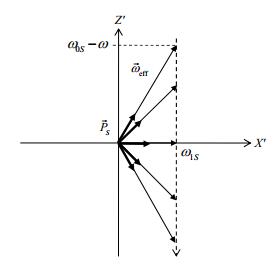
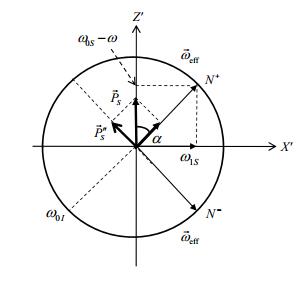
假设微波场幅度为B1沿X方向,频率ω接近于高场ESR跃迁频率,每一个自旋包都可以看做在旋转坐标系中以角频率ω旋转,如图 6所示.每一个自旋包都会经历一个有效场(Beff):
| $ {\overrightarrow B _{{\rm{eff}}}} = \sqrt 2 {B_1}\overrightarrow x + \left( {\frac{{{\omega _{0S}} - \omega }}{{{\gamma _S}}}} \right)\overrightarrow z $ | (6) |
|
图 6 旋转坐标系下两个自旋包经历的有效场{来自文献[26]} Figure 6 The effective fields in the rotating frame experienced by these two spin packets {from ref. [26]} |
ω0S=γSB0,是电子Larmor频率,γS是电子旋磁比,B0是静磁场强度.Beff与静磁场B0夹角为α.常数因子
当ωeff=γSBeff=ω0I时(ωeff为有效频率),即旋转坐标系下的电子有效频率等于核的Larmor频率时,电子极化通过超精细偶合转移给核自旋.电子极化PS方向始终沿着静磁场B0,因此只有沿着有效场PS "=PScosα分量参与极化转移,限制了极化转移的效率.另外,两个自旋包的有效频率方向相反,图 6所示,一个为PScosα,另一个为-PScosα,会相互抵消一部分.核的极化PI最终净极化转移为:
| $ \frac{{{\rm{d}}{P_I}}}{{{\rm{d}}t}} \approx \left( {{N^ - } - {N^ + }} \right){P_S}\cos \alpha $ | (7) |
因此称为微分固态效应(Differential Solid Effect, DSE),明显看到电子极化的转移效率受到有效场方向和各个自旋包的影响,降低了极化转移的效率.
1.3.2 完整固态效应1988年,Henstra提出ISE,利用绝热快速通过方法避免了自旋包极化相互抵消,从而高效的将电子极化转移到核,解决了当电子ESR谱宽大于核Larmor频率时,极化效率低的问题.绝热快速通过方法,通过固定外磁场快速微波扫频,或用一定频率的高功率微波照射自旋系统并快速扫描外磁场实现电子到核的极化转移.
假设沿X方向加一个振荡微波场B1cos(ωt)连续照射样品分子,并不断变化微波的频率ω或外磁场强度B0.当旋转坐标系下的电子有效频率等于实验室坐标系下核的频率,即满足Hartmann-Hahn条件时[(8) 式],电子向核的极化转移效率最高.
| $ {\omega _{{\rm{eff}}}} = \sqrt {{{\left( {{\omega _{0S}} - \omega } \right)}^2} + \omega _{1S}^2} = {\omega _{0I}} $ | (8) |
(8) 式中,ωeff是旋转坐标系下电子有效频率,ω1S是电子Rabi频率,B1是微波场强度;ω是微波的频率,ω0S=γSB0和ω0I=γIB0分别是电子与核的Larmor频率,B0是外磁场强度.
当微波的频率快速绝热改变,电子磁化矢量PS的方向会始终与有效频率ωeff方向保持一致,如图 7所示,这个过程称为绝热快速通过(绝热扫描外磁场原理一样),MIONP中扫频时间受到电子的纵向弛豫时间限制.
ISE过程必须满足两个条件:(1)绝热快速通过:
图 8描述了旋转坐标系下的ISE过程,在A(N+)和B(N-)点满足ωeff=ω0I发生极化转移,电子磁化矢量方向始终与有效场平行,能够完全利用电子极化PS,而不只是分量PScosα.并且在A和B点的电子极化不会抵消,当微波频率绝热快速通过整个ESR的谱,每个自旋包都会有贡献:
| $ \frac{{{\rm{d}}{P_I}}}{{{\rm{d}}t}} \approx \sum\limits_i {{N^i}{P_S}} $ | (9) |
Ni为自旋包位置ωSi处的参与ISE过程的电子数.
需要注意的是,Takeda等人[5, 39]认为,由于ISE过程中利用了交叉极化,因此将此方法称为完整交叉极化(Integrated Cross Polarization,ICP).我们认为“完整固态效应”这个称谓描述的是应用范围,克服了电子的ESR谱宽大于核的Larmor频率时,固态效应极化转移效率低的问题.而“完整交叉极化”针对的是实验过程中涉及到了交叉极化原理.不论哪种称谓,实验方法是一致的,都通过绝热快速通过扫场或扫频.
1.4 核自旋系综的极化当激光停止照射后,三重态电子自发跃迁到基态时,极化剂分子又变为逆磁性,核的纵向弛豫时间增加.相对于传统的DNP,这也是优势之一.最初只有电子三重态附近与之偶合的质子会获得极化增强,然后通过自旋扩散,这些核的极化传递给其他的核,最终得到核系综的极化增强.
2 实验条件与应用为了提高MIONP的效率,必须对实验条件进行优化.影响实验的因素包括:三重态分子的浓度、激光条件、实验温度、三重态电子的极化度和寿命、极化转移到核的效率、原子核的扩散效率和弛豫时间等.本章详细介绍了三重态样品的性质,脉冲序列的优化,以及实验温度的控制3个方面的因素.
2.1 实验样品芳香类有机分子晶体是目前MIONP研究中重要的三重态分子.1967年,首次在蒽(ANThracene,ANT)发现了ONP效应,随后大量的三重态样品在实验中被广泛使用.1980年,MIONP首次在对二溴苯参杂对二氯代苯中实现[25].至今已经有大量的MIONP样品得到了应用和研究,如芴掺杂菲[40-42]、芴掺杂氮蒽[43]、萘参杂并五苯[26, 39, 44-46]、三联苯掺杂并五苯[47]和萘参杂对三联苯[48].
在一个特定的ONP实验系统中,不同的三重态物质需要的条件不同.相比于蒽:苯四甲腈=1:1混合晶体样品的电子激发[49],在并五苯参杂的ONP实验中,局部有更高的电子三重态.另外必须考虑样品中电子纵向弛豫时间和电子三重态寿命的影响.在芴掺杂菲的系统中,电子纵向弛豫时间远小于电子三重态寿命,导致在电子极化转移到核之前,会恢复到热力学极化的状态.这种情况下由于电子依旧是玻尔兹曼热平衡态,需要强外场和非常低的温度,才能达到高的极化度.但是MIONP实验中,三重态分子能循环利用,可以通过快速的重复光激发来实现高效的ISC过程.当电子纵向弛豫时间远大于电子三重态寿命(如萘掺杂并五苯分子系统),在电子极化转移到核的过程中,电子始终处于高的极化态.
随着实验技术的发展,MIONP的研究范围在不断的扩大,从初始的单晶样品,到应用范围更广的多晶样品[39, 48, 50],再到薄片样品[51]以及玻璃基质样品(glassy matrix)[52].对于MIONP实验,激光照射深度十分重要,并且晶体排列的方向必须一致,才能保证更高的极化效率.
当选择好三重态样品后,必须考虑样品中电子与核的自旋密度[53]、样品的弛豫时间、三重态电子的弛豫时间[54]等因素.核的极化P(t)随这些参数的变化如下式[52]:
| $ P\left( t \right) = \frac{{{P_e}}}{{1 + \frac{{{T_B}}}{{{T_1}}}}}\left\{ {1 - \exp \left[ { - \left( {\frac{1}{{{T_1}}} + \frac{1}{{{T_B}}}} \right)t} \right]} \right\} $ | (10) |
Pe为极化转移前电子的极化度,T1是1H核的纵向弛豫时间.TB与初始极化建立曲线的斜率成反比,根据
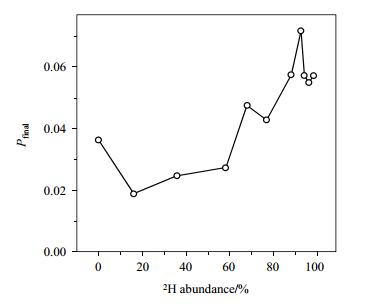
样品中质子浓度影响最终的极化增强[31, 55].如图 9所示,利用摩尔比1:2 000的并五苯参杂的三联苯单晶,并且三联苯的氘化程度不同.纵轴表示1H核的极化度,横轴表示2H核的比例.可以观察到在不同的氘化比例下,质子极化度不同,并且有文献[56]发现对2H核去偶,会加速质子的自旋扩散过程.
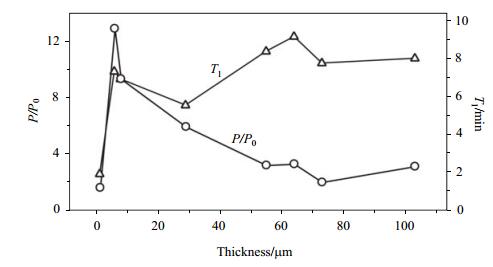
2.1.2 样品厚度样品厚度影响了质子的弛豫时间[48, 51],进而影响质子极化增强.如图 10所示,三角形线代表样品厚度与质子纵向弛豫时间的关系,空心圆线代表了极化增强与样品厚度的关系.
|
图 10 极化增强和质子纵向弛豫时间与样品厚度的关系{来自文献[51]} Figure 10 The nuclear polarization enhancement and T1 versus sample thickness {from ref. [51]} |
为了能够激发三重态分子从基态跃迁到第一激发态(S0→S1),必须有1个匹配波长的激光才能实现最大的效率.目前的实验中,大量的激光器得到应用,包括氮气激光器、准分子激光器、氩离子激光器、固体激光器和闪光灯泵浦染料激光器.这些激光器利用高功率脉冲输出.实验用的固态三重态分子,大多具有多重的最大吸收峰,可以利用不同的光源.通常情况下,激光的功率越大,电子极化的速率越快[50].但是由于激光对样品的加热效应很大,限制了功率的大小[53].利用脉冲激光重复激发样品,可以大幅提高MIONP的效率.对于MIONP实验,所需的激光束照射必须满足两个条件[47]:(1)激光束照射样品引起的S0→S1吸收跃迁必须大于S1→S0的辐射衰变的强度;(2)激光的脉宽必须大于样品单重态的寿命,小于三重态的寿命.
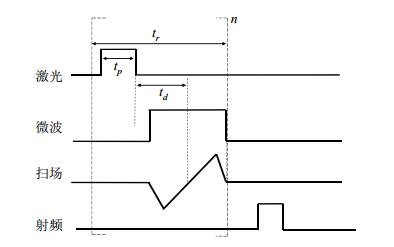
在最近的文献[44, 53, 54]中,已经对激光的脉宽、ISE重复率、脉冲功率、延迟时间等条件进行了实验和理论的探讨如图 11所示MIONP序列,对激光脉宽(tp)、延迟时间(td)、重复时间(tr,对应重复率R)进行优化,tr即ISE过程时间,n为重复次数.
2.2.1 ISE重复率如图 12所示,利用萘参杂并五苯样品,在温度为40 K场强为0.3 T条件下进行实验,使用515 nm的盘形激光器,Eichhorn等人[51]研究了ISE重复率(分别为4 kHz、1 kHz和500 Hz)与质子极化度(P)的关系,结果显示:重复率越小,质子的极化度也越大,但极化建立的速度越慢.在400 Hz的重复率下,质子极化度大于40%.相同的实验现象在其他文献[31, 44, 54]中也得到证实.

|
图 12 不同ISE重复率与质子极化度的关系{来自文献[57]} Figure 12 Proton polarization versus different repetition rates of the ISE sequence{from ref. [57]} |
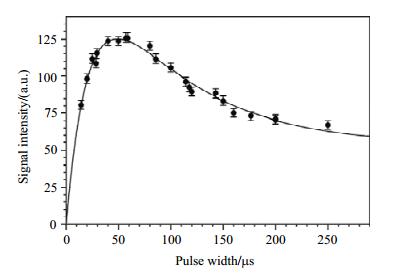
激光脉冲的性质,如形状[47]和脉宽[53, 54],对质子的极化增强也有很大影响.图 13[54]表明了激光脉宽与质子信号强度的关系.这个实验在室温下进行,利用并五苯参杂三联苯样品,在0.3 T场强下,514 nm的氩离子激光器激发基态向第一激发态的跃迁.
MIONP序列优化中,对激光脉宽和重复率的研究最为广泛.由于延迟时间td很短,在大部分的实验中都不予考虑.但是延迟时间也是一个有用的参数,能够反映三重态电子能级的跃迁以及三重态子能级的性质[54].
2.3 温度和磁场的控制温度影响样品的弛豫时间[53, 54],从而影响质子的极化增强效率,因此对温度的控制也十分重要.在室温下的MIONP增强[36, 58],已经达到2.5×105倍,相应的质子极化度达到了34%[55].
目前MIONP实验多是在0.35 T场强[36, 48, 56]附近进行,但是在2.7 T(微波75 GHz)的场强下也有实验[43]进行.此外日本的研究小组将变场技术应用到MIONP中,在0.3 T场强的电磁体中,实现ISE过程,再将样品送到11.7 T的低温超导磁体中进行NMR检测,并且利用交叉极化实现了13C核的极化增强[27].
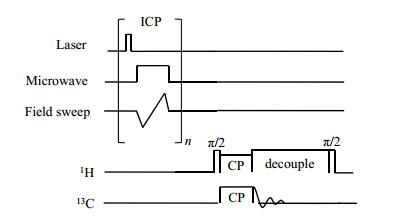
2.4 非质子核的MIONP实验利用MIONP技术先将质子极化,再通过传统的核间交叉极化[59]可以实现其他核(如13C核[5]和19F核[55])的极化增强.13C的MIONP序列如图 14所示,与质子的MIONP序列相比,仅仅在序列中添加一个类似固体NMR中的交叉极化(Cross Polarization, CP)序列.
|
图 14 MIONP实现13C核极化增强的脉冲序列{来自文献[5]} Figure 14 A pulse sequence for the enhanced 13C signal detection using MIONP{from ref. [5]} |
利用三联苯参杂并五苯样品,在0.35 T场强和室温下进行实验.图 15(a)表示先经过ICP过程增加1H核的极化度,再经过CP过程实现13C核的极化增强谱;图 15(b)表示直接通过CP过程得到13C NMR谱.结果表明MIONP技术极大地增强了13C NMR信号.

|
图 15 13C核的MIONP极化增强对比图谱{来自文献[5]} Figure 15 The 13C spectra with (a) and without (b) MIONP{from ref. [5]} |
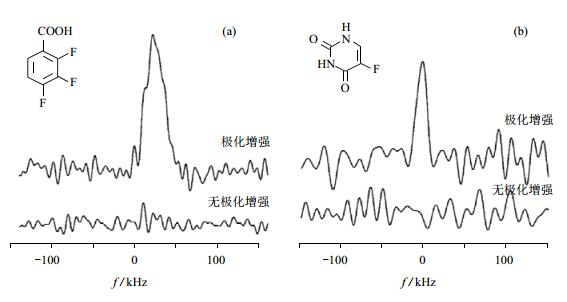
在0.4 T场强和120 K温度条件下,利用玻璃基质的19F核(2, 3, 4-三氟苯甲酸和5-氟尿嘧啶两种含氟样品)参杂的三联苯样品.先将质子极化,再通过变场方法将极化转移到19F核,实现19F核的极化增强[52].实验结果图 16所示,图 16(a)(2, 3, 4-三氟苯甲酸)和图 16(b)(5-氟尿嘧啶)上方的谱为极化增强谱,底部的谱为热力学平衡谱(无极化增强谱).结果表明MIONP技术极大地增强了19F NMR信号.
|
图 16 两种不同含氟化合物19F核的MIONP极化增强对比谱{来自文献[52]}. (a) 2, 3, 4-三氟苯甲酸;(b) 5-氟尿密啶 Figure 16 The 19F NMR spectra with and without MIONP using two different fluorochemicals {from ref. [52]}.(a) 2, 3, 4-trifluorobenzoic acid; (b) 5-fluorouracil |
MIONP从诞生至今已经发展30多年,广泛的应用到光化学和光物理实验.利用各种三重态芳香烃分子晶体,实现了不同晶体物质的质子极化增强,并且可以通过交叉极化将质子极化再转移到其他核.目前MIONP大多是基础方法的研究,没有得到广泛的应用.样品集中于单晶和多晶样品,限制了其应用范围,并且大多是在1H核,对于其他核的研究很少.但是MIONPO已经实现了高的质子极化度,更重要的是在室温下的MIONP实验研究,已经得以大力发展并且取得了很好的结果.在以后的实验中可以利用交叉极化将1H核的极化度转移给其他核,来实现高分辨的NMR;多晶样品和玻璃基质样品的极化增强,扩大了样品的应用范围,并且已经实现薄片样品的极化增强,这种方法有可能发展到生物体系中;利用变场的方法,在低场实现核极化过程,然后在高场检测,能应用到高分辨NMR/MRI.我们相信未来在生物、医学研究中,MIONP会有一席之地.
| [1] | GERSHENFELD N A, CHUANG I L. Bulk spin-resonance quantum computation[J]. Science, 1997, 275(5298): 350-356. DOI: 10.1126/science.275.5298.350. |
| [2] | PENG X H, SUTER D. Spin qubits for quantum simulations[J]. Front Phys China, 2010, 5(1): 1-25. DOI: 10.1007/s11467-009-0067-x. |
| [3] | LI Z K, ZHOU H, JU C Y, et al. Experimental realization of a compressed quantum simulation of a 32-spin Ising chain[J]. Phys Rev Lett, 2014, 112(22): 220501. DOI: 10.1103/PhysRevLett.112.220501. |
| [4] | VLAARDINGERBROEK M T, BOER J A. Magnetic resonance imaging[M]. 2nd ed. Berlin: Springer-Verlag, 1999. |
| [5] | TAKEDA K. Studies on dynamic nuclear polarization using photo-excited triplet electron spins[D]. Kyoto:Kyoto University, 2003. |
| [6] | CHERUBINI A, PAYNE G, LEACH M, et al. Hyperpolarising 13C for NMR studies using laser-polarised 129Xe:SPINOE vs thermal mixing[J]. Chem Phys Lett, 2003, 371(5): 640-644. |
| [7] |
LI H D, ZHAN Z Y, HAN Y Q, et al. Lung MRI use Hyperpolarized gase[J].
Chinese J Magn Reson, 2014, 31(3): 307-320.
李海东, 张智颖, 韩叶清, 等. 超级化气体肺部磁共振成像[J]. 波谱学杂志, 2014, 31(3): 307-320. |
| [8] | GOLMAN K, AXELSSON O, JÓHANNESSON H, et al. Parahydrogen-induced polarization in imaging:Subsecond 13C angiography[J]. Magn Reson Med, 2001, 46(1): 1-5. DOI: 10.1002/mrm.v46:1. |
| [9] | BLÄTTLER C, JENT F, PAUL H. A novel radical-triplet pair mechanism for chemically induced electron polarization (CIDEP) of free radicals in solution[J]. Chem Phys Lett, 1990, 166(4): 375-380. DOI: 10.1016/0009-2614(90)85046-F. |
| [10] | OVERHAUSER A W. Paramagnetic relaxation in metals[J]. Physical Review, 1953, 89(4): 689-790. DOI: 10.1103/PhysRev.89.689. |
| [11] | LUMATA L L, MARTIN R, JINDAL A K, et al. Development and performance of a 129-GHz dynamic nuclear polarizer in an ultra-wide bore superconducting magnet[J]. MAGMA, 2015, 28(2): 195-205. DOI: 10.1007/s10334-014-0455-2. |
| [12] | POLYON C, LURIE D, YOUNGDEE W, et al. Field-cycled dynamic nuclear polarization (FC-DNP) of 14N and 15N nitroxide radicals at low magnetic field[J]. J Phys D Appl Phys, 2007, 40(18): 5527-5532. DOI: 10.1088/0022-3727/40/18/002. |
| [13] | NEUDERT O, MATTEA C, STAPF S, et al. Fast-field-cycling relaxometry enhanced by dynamic nuclear polarization[J]. Micropor Mesopor Mat, 2015, 205: 70-74. DOI: 10.1016/j.micromeso.2014.07.036. |
| [14] | JANNIN S, COMMENT A, KURDZESAU F, et al. A 140 GHz prepolarizer for dissolution dynamic nuclear polarization[J]. J Chem Phys, 2008, 128(24): 241102. DOI: 10.1063/1.2951994. |
| [15] | JANNIN S, BORNET A, COLOMBO S, et al. Low-temperature cross polarization in view of enhancing dissolution dynamic nuclear polarization in NMR[J]. Chem Phys Lett, 2011, 517(4): 234-236. |
| [16] | HAZE O, CORZILIUS B R, SMITH A A, et al. Water-soluble narrow-line radicals for dynamic nuclear polarization[J]. J Am Chem Soc, 2012, 134(35): 14287-14290. DOI: 10.1021/ja304918g. |
| [17] | ZHOU J W, LI L Y, HU H B, et al. Study of natural diamonds by dynamic nuclear polarization-enhanced 13C nuclear magnetic resonance spectroscopy[J]. Solid State Nucl Magn Reson, 1994, 3(6): 339-351. DOI: 10.1016/0926-2040(94)90018-3. |
| [18] |
HE Y G, FENG J W, ZHANG Z, et al. Development of pulsed dynamic nuclear polarization for enhancing NMR and MRI[J].
Chinese J Magn Reson, 2015, 32(2): 393-398.
贺玉贵, 冯继文, 张志, 等. 脉冲动态核极化增强的NMR和MRI系统研究[J]. 波谱学杂志, 2015, 32(2): 393-398. DOI: 10.11938/cjmr20150221. |
| [19] | HE Y G, FENG J W, ZHANG Z, et al. A peripheral component interconnect express-based scalable and highly integrated pulsed spectrometer for solution state dynamic nuclear polarization[J]. Rev Sci Instrum, 2015, 86(8): 083101. DOI: 10.1063/1.4927453. |
| [20] | HE Y G, ZHANG Z, FENG J W, et al. Simultaneous acquisition of multi-nuclei enhanced NMR/MRI by solution state dynamic nuclear polarization[J]. Sci China Chem, 2016, 59(7): 830-835. DOI: 10.1007/s11426-015-0512-0. |
| [21] | MAIER G, HAEBERLEN U, WOLF H, et al. Optische kernspin-polarisation in anthracen-kristallen[J]. Phys Lett A, 1967, 25(5): 384-385. DOI: 10.1016/0375-9601(67)90712-8. |
| [22] | GROVER B. Noble-gas NMR detection through noble-gas-rubidium hyperfine contact interaction[J]. Phys Rev Lett, 1978, 40(6): 391-392. DOI: 10.1103/PhysRevLett.40.391. |
| [23] | JEFFRIES C. Some new schemes for polarizing nuclei[J]. Phys Rev Lett, 1967, 19(21): 1221-1224. DOI: 10.1103/PhysRevLett.19.1221. |
| [24] | LAMPEL G. Nuclear dynamic polarization by optical electronic saturation and optical pumping in semiconductors[J]. Phys Rev Lett, 1968, 20(10): 491-493. DOI: 10.1103/PhysRevLett.20.491. |
| [25] | DEIMLING M, BRUNNER H, DINSE K, et al. Microwave-induced optical nuclear polarization (MI-ONP)[J]. J Magn Reson, 1980, 39(2): 185-202. |
| [26] | HENSTRA A, LIN T S, SCHMIDT J, et al. High dynamic nuclear polarization at room temperature[J]. Chem Phys Lett, 1990, 165(1): 6-10. DOI: 10.1016/0009-2614(90)87002-9. |
| [27] | KAGAWA A, NEGORO M, TAKEDA K, et al. Magnetic-field cycling instrumentation for dynamic nuclear polarization-nuclear magnetic resonance using photoexcited triplets[J]. Rev Sci Instrum, 2009, 80(4): 044705. DOI: 10.1063/1.3123346. |
| [28] | IINUMA M. Dynamic nuclear polarization at high temperature for polarized proton target[D]. Kyoto:Kyoto University, 1997. |
| [29] | IINUMAM, TAKAHASHIY, SHAKÉI, 等. High proton polarization by microwave-induced optical nuclear polarization at 77 K[J]. Phys Rev Lett, 2000, 84(1): 171. |
| [30] | BLOEMBERGEN N. On the interaction of nuclear spins in a crystalline lattice[J]. Physica, 1949, 15(3): 386-426. |
| [31] | KAGAWA A, MUROKAWA Y, TAKEDA K, et al. Optimization of 1H spin density for dynamic nuclear polarization using photo-excited triplet electron spins[J]. J Magn Reson, 2009, 197(1): 9-13. DOI: 10.1016/j.jmr.2008.11.009. |
| [32] | HENSTRA A, DIRKSEN P, SCHMIDT J, et al. Nuclear spin orientation via electron spin locking (NOVEL)[J]. J Magn Reson, 1988, 77(2): 389-393. |
| [33] | HAUSSER K. Optical spin polarization in molecular crystals[J]. Pure Appl Chem, 1972, 32(1-4): 183-196. |
| [34] | YANG T C, SLOOP D J, WEISSMAN S, et al. Zero-field magnetic resonance of the photo-excited triplet state of pentacene at room temperature[J]. J Chem Phys, 2000, 113(24): 11194-11201. DOI: 10.1063/1.1326069. |
| [35] | SLOOP D J, YU H L, LIN T S, et al. Electron spin echoes of a photoexcited triplet:Pentacene in p-terphenyl crystals[J]. J Chem Phys, 1981, 75(8): 3746-3757. DOI: 10.1063/1.442520. |
| [36] | TAKEDA K, TAKEGOSHI K, TERAO T. Dynamic nuclear polarization by electron spins in the photoexcited triplet state:Ⅱ. High polarization of the residual protons in deuterated naphthalene[J]. J Phys Soc Jpn, 2004, 73(8): 2319-2322. DOI: 10.1143/JPSJ.73.2319. |
| [37] | MCCONNELL H M, CHESNUT D B. Theory of isotropic hyperfine interactions in π-electron radicals[J]. J Chem Phys, 1958, 28(1): 107-117. DOI: 10.1063/1.1744052. |
| [38] | WENCKEBACH W T. The solid effect[J]. Appl Magn Reson, 2008, 34(3, 4): 227-235. |
| [39] | TAKEDA K, TAKEGOSHI K, TERAO T. Dynamic nuclear polarization by electron spins in the photoexcited triplet state:I. Attainment of proton polarization of 0.7 at 105 K in naphthalene[J]. J Phys Soc Jpn, 2004, 73(8): 2313-2318. DOI: 10.1143/JPSJ.73.2313. |
| [40] | VAN KESTEREN H, WENCKEBACH W T, SCHMIDT J. The mechanism of microwave-induced optical nuclear polarization in fluorene doped with phenanthrene:A qualitative analysis[J]. Chem Phys Lett, 1985, 121(4): 440-445. |
| [41] | VAN KESTEREN H, WENCKEBACH W T, SCHMIDT J. The mechanism of microwave induced optical nuclear polarization in the system fluorene doped with phenanthrene:A quantitative analysis[J]. Mol Phys, 1986, 58(2): 263-271. DOI: 10.1080/00268978600101131. |
| [42] | PENFOLD J, WARD R, WILLIAMS W. A time-of-flight neutron reflectometer for surface and interfacial studies[J]. J Phys E Sci Instrum, 1987, 20(11): 1411-1417. DOI: 10.1088/0022-3735/20/11/024. |
| [43] | VERHEIJ P F, WENCKEBACH W T, SCHMIDT J. Microwave induced optical nuclear polarization at 75 GHz:A quantitative analysis[J]. Appl Magn Reson, 1993, 5(2): 187-205. DOI: 10.1007/BF03162521. |
| [44] | EICHHORN T R, HAAG M, VAN DEN BRANDT B, et al. An apparatus for pulsed ESR and DNP experiments using optically excited triplet states down to liquid helium temperatures[J]. J Magn Reson, 2013, 234: 58-66. DOI: 10.1016/j.jmr.2013.06.009. |
| [45] | EICHHORN T, BRANDT BVD, HAUTLE P, et al. Dynamic nuclear polarisation via the integrated solid effect Ⅱ:experiments on naphthalene-h 8 doped with pentacene-d14[J]. Mol Phys, 2014, 112(13): 1773-1782. DOI: 10.1080/00268976.2013.863405. |
| [46] | IINUMAM, SHAKÉI, TAKIZAWAR, 等. High proton polarization in crystalline naphthalene by dynamic nuclear polarization with laser excitation at room temperature and liquid nitrogen temperature[J]. Phys Lett A, 1995, 208(3): 251-256. |
| [47] | TAKEDA K, YAMAMURA T, KAGAWA A, et al. Enhancement of efficiency in photo-excitation to the triplet state by laser-pulse reshaping[J]. J Magn Reson, 2005, 174(2): 310-313. DOI: 10.1016/j.jmr.2005.03.004. |
| [48] | TAKEDA K, TAKEGOSHI K, TERAO T. Zero-field electron spin resonance and theoretical studies of light penetration into single crystal and polycrystalline material doped with molecules photoexcitable to the triplet state via intersystem crossing[J]. J Chem Phys, 2002, 117(10): 4940-4946. DOI: 10.1063/1.1499124. |
| [49] | ALLGEIER J, BUNTKOWSKY G, HENTRICH S, et al. Optical nuclear polarization of deuterium spins:mechanisms and applications in solid state NMR[J]. Isr J Chem, 1992, 32(2, 3): 205-213. |
| [50] | TAKEDA K, TAKEGOSHI K, TERAO T. Dynamic nuclear polarization by photoexcited-triplet electron spins in polycrystalline samples[J]. Chem Phys Lett, 2001, 345(1): 166-170. |
| [51] | TATEISHI K, NEGORO M, KAGAWA A, et al. Hyperpolarization of thin films with dynamic nuclear polarization using photoexcited triplet electrons[J]. J Phys Soc Jpn, 2013, 82(8): 084005. DOI: 10.7566/JPSJ.82.084005. |
| [52] | TATEISHI K, NEGORO M, KAGAWA A, et al. Dynamic nuclear polarization with photoexcited triplet electrons in a glassy matrix[J]. Angew Chem, 2013, 125(50): 13549-13552. DOI: 10.1002/ange.201305674. |
| [53] | SAKAGUCHI S, UESAKA T, KAWAHARA T, et al. Proton polarization in photo-excited aromatic molecule at room temperature enhanced by intense optical source and temperature control[J]. Nuclear Instru and Meth Phys Res B:Beam Interactions with Materials and Atoms, 2013, 317: 679-684. DOI: 10.1016/j.nimb.2013.07.067. |
| [54] | KAWAHARA T, SAKAGUCHI S, TATEISHI K, et al. Kinetic parameters of photo-excited triplet state of pentacene determined by dynamic nuclear polarization[J]. J Phys Soc Jpn, 2015, 84(4): 044005. DOI: 10.7566/JPSJ.84.044005. |
| [55] | TATEISHI K, NEGORO M, NISHIDA S, et al. Room temperature hyperpolarization of nuclear spins in bulk[J]. P Natl Acad Sci USA, 2014, 111(21): 7527-7530. DOI: 10.1073/pnas.1315778111. |
| [56] | NEGORO M, NAKAYAMA K, TATEISHI K, et al. 2H-decoupling-accelerated 1H spin diffusion in dynamic nuclear polarization with photoexcited triplet electrons[J]. J Chem Phys, 2010, 133(15): 154504. DOI: 10.1063/1.3493453. |
| [57] | EICHHORN T, HAAG M, VAN DEN BRANDT B, et al. High proton spin polarization with DNP using the triplet state of pentacene-d14[J]. Chem Phys Lett, 2013, 555: 296-299. DOI: 10.1016/j.cplett.2012.11.007. |
| [58] | IINUMAM, TAKAHASHIY, SHAKÉI, 等. Proton polarization with p-terphenyl crystal by integrated solid effect on photoexcited triplet state[J]. J Magn Reson, 2005, 175(2): 235-241. |
| [59] | PINES A, GIBBY M, WAUGH J. Proton-enhanced NMR of dilute spins in solids[J]. J Chem Phys, 1973, 59(2): 569-590. DOI: 10.1063/1.1680061. |
 2017, Vol. 34
2017, Vol. 34