2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
铷原子频标因具有体积小、功耗低、综合性能好的特点,已被广泛应用于需要高精度时间频率基准的诸多领域.作为全球卫星导航系统的核心部件,铷原子频标性能的高低将直接决定导航系统定位精度的优劣.在卫星导航系统中,对于星载铷频标,其长期频率稳定度是关键性能指标,而影响长期稳定度的因素有光频移、压力频移、磁致频移、微波功率频移等.外界磁场的波动,如地磁场波动,将对物理系统内部静磁场(C场)产生影响,并通过磁致频移效应影响铷频标的频率稳定度,因而实用的铷频标常采用磁屏蔽筒来屏蔽外界磁场波动.为了研究磁屏蔽筒的磁屏蔽性能,本文选取了实验室自行研制的一台铷原子频标,首先测量磁屏蔽筒的轴向磁屏蔽因子,然后评估了地磁场日波动对铷频标长期频率稳定度的影响.
1 铷频标磁场测量原理及方法 1.1 铷频标物理系统的磁屏蔽因子为了评估铷频标物理系统磁屏蔽筒的磁屏蔽性能,定义磁屏蔽因子(S)为
| $ S = \frac{{\mathit{\Delta }{B_{{\rm{ex}}}}}}{{\mathit{\Delta }{B_{{\rm{in}}}}}} $ | (1) |
其中△Bex为磁屏蔽筒外部磁场强度变化值,△Bin为物理系统内部磁场强度变化值.
S数值越大,表明磁屏蔽筒对外界静磁场的屏蔽性能越好.对于外部磁场强度可以用高斯计直接测量.对于物理系统内部的磁场强度,由于磁屏蔽因子较大,外部磁场强度变化时,内部磁场强度变化小,测量误差较大.为了提高内部磁场强度的测量精确度,可以利用87Rb原子基态超精细Zeeman能级跃迁频率与周围静磁场强度的关系,间接得到内部磁场强度的大小.
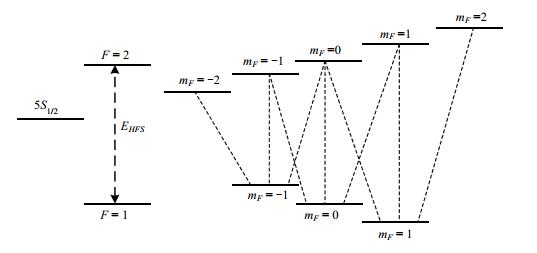
1.2 87Rb原子Zeeman跃迁87Rb原子基态是5S1/2态,由于铷原子核磁矩与电子磁矩相互作用,5S1/2态分裂为F = 2和F = 1两个超精细能级.在外加静磁场下,87Rb原子基态F能级进一步分裂,形成了(2F+1)个超精细Zeeman能级(图 1).
|
图 1 87Rb原子基态超精细Zeeman能级图 Figure 1 Hyperfine Zeeman transition between 87Rb ground states |
根据超精细Zeeman能级的跃迁选择定则,基态5S1/2态的F = 2和F = 1的超精细Zeeman能级之间存在9种跃迁(图 1),可以观察到7条跃迁谱线.其中(F = 2,mF= 0)-(F = 1,mF= 0)的跃迁被称为0-0跃迁,对外加磁场不敏感,被选为铷原子频率标准[1].其它跃迁的中心频率值与磁场强度呈线性关系,被称为磁敏跃迁,可以用来测量铷原子周围的磁场强度.
实验中选取的物理系统微波腔场模式近似为TE011模式[2],假定铷原子周围磁场强度变化为△Bin时,磁敏能级(F = 2,mF= −1)-(F = 1,mF= −1)跃迁谱线中心频率的偏移为δv,在弱磁场条件下,由Breit-Rabi公式[3]可计算得δv(单位为Hz/nT)与△Bin关系为:
| $ \delta v = \mathit{\Delta }{B_{{\rm{in}}}} \times 14 $ | (2) |
(2) 式给出了Zeeman能级中心跃迁频率与内部磁场强度变化之间的关系,因此内部磁场强度变化可以通过测量Zeeman能级中心跃迁频率间接得到.
由于铷频标光学微波双共振信号的吸收峰对应的频率为超精细Zeeman能级的中心跃迁频率,因此可以通过测量铷频标光学微波双共振信号的吸收峰对应的频率间接得到Zeeman能级的中心跃迁频率.在双共振信号的谱线中,透射光强(It)与微波频率(v)的关系为
| $ {I_t} = {I_0}\left[ {1 - \alpha g\left( v \right)} \right] $ | (3) |
其中I0表示无微波共振时光电探测得到的直流光强,α=△I/I0为信号对比度,g(v)为双共振的吸收曲线,其线型可近似为洛伦兹线型(图 2).

|
图 2 光学微波双共振吸收谱线 Figure 2 Optical microwave double resonance spectrum |
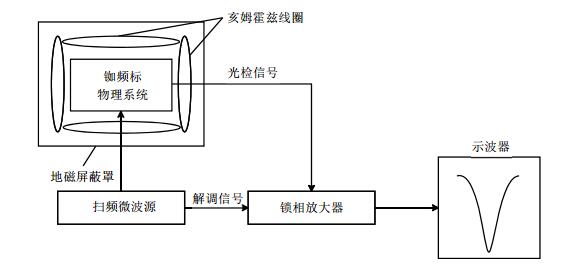
由于铷频标双共振信号很弱,无法直接测量.为了从较大的背景光电流噪声中检测出微弱的双共振信号,采取了幅度调制和解调的方法[4],实验装置如图 3所示.其工作原理为:经调幅的微波信号通入物理系统,使该微波在铷原子跃迁中心频率附近扫频得到双共振信号,利用锁相放大器对该信号进行同步解调得到能级跃迁谱线.
|
图 3 光学微波双共振信号测量装置 Figure 3 The optical microwave double resonance signal measuring system |
物理系统中光电池上交流信号的幅度和输入微波频率与铷原子共振跃迁频率之间的差值有关.当微波频率与中心频率越接近,信号强度越大,经同步解调后的直流信号也越大,可以通过跃迁信号最大值对应的频率值初步确定跃迁谱线中心频率值.
为了较精确确定跃迁频率值,将微波场改为调频微波场,光检信号通过锁相放大器后,得到铷频标物理系统的S曲线(鉴频曲线),其为光学微波双共振吸收谱线的一阶微分(图 4).双共振吸收谱线上的峰值所对应的频率值,在一阶微分线型的S曲线中是零点对应的位置.利用锁相放大器,采用过零检测的方法,即可以较精确地确定跃迁中心频率.

|
图 4 鉴频曲线 Figure 4 Frequency discrimination curve |
实验中对物理系统加上轴向方向的外加磁场,通过测量不同外加磁场强度Bex下的磁敏跃迁中心频率,得到不同外加磁场下的内磁场强度Bin,通过(1) 式即可计算出铷频标物理系统静磁屏蔽筒的轴向磁屏蔽因子.为了屏蔽地磁场的干扰,将铷频标物理系统和产生外加磁场的亥姆霍兹线圈均放置于地磁屏蔽罩中.
2 结果与讨论 2.1 磁屏蔽因子的计算实验中选取了实验室自行研制的一套铷频标物理系统进行磁屏蔽因子的测量.铷频标物理系统的静磁屏蔽系统由内外两层静磁屏蔽筒构成,静磁屏筒材料是1J85坡莫合金,其中内层磁屏筒内径为35 mm,厚度为0.5 mm,长度为50 mm;外层磁屏蔽筒内径为45 mm,厚度为1 mm,长度为100 mm.内层磁屏蔽筒有通光孔使抽运光入射到滤光泡中,且因物理系统走线的原因,在轴向磁屏蔽筒上开孔,这两个原因可能使得磁屏蔽筒的磁屏蔽性能下降.为了评估磁屏蔽筒的轴向磁屏蔽性能对铷频标长期稳定度产生的影响,对轴向磁屏蔽因子进行了测量.
实验时调节亥姆霍兹线圈电流改变外加磁场Bex的强度,得到多组跃迁谱线中心频率如表 1所示.
| 表 1 跃迁谱线中心频率随外加磁场(Bex)的变化 Table 1 Zeeman transition frequency in different external magnetic fields |
根据表 1,利用(2) 式,可以计算得到磁屏蔽筒内部的磁场强度Bin,计算结果见表 2.
| 表 2 轴向外加磁场(Bex)与内磁场(Bin)的对应关系 Table 2 The correlations between external axial (Bex) and inner (Bin) magnetic field |
利用表 2中的数据,绘制出Bex与Bin的关系图(图 5),并对Bex与Bin进行线性拟合.

|
图 5 轴向外加磁场(Bex)与内磁场(Bin)的关系曲线 Figure 5 The correlations between external axial (Bex) and inner (Bin) magnetic field |
根据(1) 式,图 5中线性拟合的曲线斜率为磁屏蔽因子S,大小为3 828,因此由于磁屏蔽筒的存在,内部磁场受外磁场波动的影响大大减小.
2.2 外部地磁场的影响分析一级近似下的Breit-Rabi公式中,0-0跃迁中心频率与周围磁场强度不敏感.在二级近似下,当87Rb原子周围存在强度为B0的静磁场时,0-0跃迁中心频率v0会发生偏移,偏移量δv为[3].
| $ \delta v = 575.14 \times {10^8}B_0^2 $ | (4) |
对于(4) 式,当周围磁场强度B0是定值时,只影响v0的准确度.当周围磁场强度B0变化ΔB0时,对0-0跃迁中心频率v0准确度(σ)造成的影响为
| $ \sigma = \mathit{\Delta }\left( {\frac{{\delta v}}{{{v_0}}}} \right) = 16.83 \times {B_0} \times \mathit{\Delta }{B_0} $ | (5) |
铷频标在地面工作时,处于地磁场环境中,地磁场的波动会对0-0跃迁中心频率产生影响.地磁场强度在地球不同位置的波动会有一定的差异,参考北京、三亚、漠河观测站的数据[5],地磁场日波动均小于100 nT.以磁屏蔽因子S =3 828计算,地磁场日波动引起的铷频标内部磁场波动为
| $ \mathit{\Delta }{B_0} = \frac{{100}}{S}{\rm{nT}} \approx 2.61 \times {10^{ - 2}}{\rm{nT}} $ | (6) |
铷频标正常工作时,C场强度B0约为8 000 nT,根据(5) 式,可得出地磁场日波动100 nT对铷频标日频率稳定度σ的影响为
| $ \sigma = \mathit{\Delta }\left( {\frac{{\delta v}}{{{v_0}}}} \right) = 16.83 \times 8 \times {10^{ - 6}} \times 2.61 \times {10^{ - 11}} \approx 3.5 \times {10^{ - 15}} $ | (7) |
上述分析与计算的结果表明,当铷频标的磁屏蔽设计合理时,对外界磁场的屏蔽效果良好,使地磁波动对铷频标日频率稳定度的影响非常小,在3.5×10-15量级,基本可以忽略.
3 结论本文对影响铷原子频标长期频率稳定度的磁致频移相关问题进行了分析研究,介绍了一种测量铷原子频标物理系统磁屏蔽因子的方法,通过对本实验室研制的一套铷频标物理系统进行实际测量和分析计算,得到轴向磁屏蔽因子约为3 828,并在此基础上分析评估了地磁场日波动对铷原子频标稳定度的影响.结果显示当铷频标物理系统磁屏蔽因子设计合理时,可以使得地磁场日波动对铷频标产生的磁致频移得到有效控制.
| [1] | 王义遒, 王庆吉, 傅济时. 量子频标原理[M]. 北京: 科学出版社, 1986. |
| [2] |
KANG S B, LI W B, ZHONG D, et al. A preliminary study on field distribution in a slotted tube cavity[J].
Chinese J Magn Reson, 2012, 29(1): 86-91.
康松柏, 李文兵, 钟达. 开槽管微波腔中微波场分布初步研究[J]. 波谱学杂志, 2012, 29(1): 86-91. |
| [3] | VANIER J, CLAUDE A. The quantum physics of atomic frequency standard[M]. USA: CRC Press, 1989. |
| [4] | 高晋占. 微弱信号检测[M]. 北京: 清华大学出版社, 2004. |
| [5] | 中国科学院地质与地球物理研究所空间环境探测实验室: 地磁实时监测[EB/OL]. http://space.iggcas.ac.cn/Geomagnetism.html. |
 2017, Vol. 34
2017, Vol. 34 
