2. 上海卡勒幅磁共振技术有限公司, 上海 201614
2. Shanghai Colorful Magnetic Resonance Technology Co. Ltd., Shanghai 201614, China
磁共振成像(magnetic resonance imaging, MRI)具有无电离辐射、信息丰富、多模态成像和多方位成像等优点,是一种广泛使用的医学影像方法[1, 2].理想情况下,磁共振图像同一种组织中的像素点应该具有相同的灰度值,但实际采集的图像除了包含噪声与伪影之外,或多或少地存在灰度不均匀(intensity inhomogeneity, IIH或intensity non-uniformity, INU)的问题.灰度不均匀是指同一种组织在图像的不同位置灰度值不一样,也可以说图像中存在一个不均匀偏场[3].
造成磁共振图像灰度不均匀的因素有很多,但主要原因是射频线圈发射和接收信号的灵敏度分布不均匀,这一点在表面线圈中尤为明显.表面线圈由于贴近成像部位,图像信噪比高、伪影少,在MRI系统中得到广泛应用.但贴近线圈的组织与远离线圈的组织之间的信号差别较大,图像更容易存在灰度不均匀.此外,主磁场不均匀、梯度场非线性及成像物体本身都可能引入灰度不均匀[3].
轻度的灰度不均匀不会影响医生读片和诊断病情,但会影响医学图像自动化分析的应用[4].许多图像处理方法,例如分割、配准等,都是建立在“图像是均匀的”基础之上的.因此,灰度不均匀校正已成为医学图像处理的一个重要环节,并开始与其他图像处理和分析算法相互结合使用.灰度校正方法按处理的时间顺序可以分为两大类[3]:
一类是前瞻性方法.其主要思想是通过校准和改进图像采集过程来校正图像不均匀,又细分为基于水模[5]、基于多线圈[6]和基于特殊序列[7]等方法.目前,一些MRI设备上已具备这样的功能.前瞻性方法需要额外的扫描数据,会在一定程度上增加硬件的复杂程度,扫描时间也会增加;此外,该方法主要适用于由设备条件引入的不均匀,也有一定的局限性.
另一类是回溯性方法.这类方法利用图像的先验知识,通过算法对扫描得到的不均匀图像做后处理,还原出均匀的图像.此类方法较多[3, 8],可细分为基于滤波[9]、基于直方图[10]、曲面拟合[11-13]和基于分割[14, 15]等方法.
在基于分割的方法中,Li等人[15, 16]于2009年提出的连贯局部灰度聚类(coherent local intensity clustering, CLIC)算法受到较多关注.这种算法改进了常规应用于均匀图像上的模糊C均值聚类方法(fuzzy C-means clustering method, FCM),使其适用于不均匀图像的分割.该方法能同时对图像做组织分割和不均匀偏场估计.CLIC算法能完全自动实现,对初始条件的选择具有很强的鲁棒性,对结构较复杂、噪声较高或偏场严重的图像也都适用.
本文在上述工作的基础上,提出了一种结合分裂布雷格曼迭代、基于CLIC模型的灰度不均匀校正算法,并将其用于处理模拟和真实的磁共振图像,以评判该算法的有效性.
1 理论与方法 1.1 灰度不均匀校正方法概述灰度不均匀的磁共振图像可看成是由一幅均匀图像乘以一个不均匀偏场,再加上噪声组成[4]:
| $ I\left( x \right) = B\left( x \right)I'\left( x \right) + \sigma \left( x \right) $ | (1) |
其中,I(x)指我们得到的灰度不均匀磁共振图像,I'(x)是我们希望得到的均匀图像,B(x)指偏场,一般视为是光滑变化的,σ(x)表示噪声.为了求解方便,我们常把模型进一步简化为无噪声的模型:
| $ I\left( x \right) = B\left( x \right)I'\left( x \right) $ | (2) |
灰度不均匀校正就是利用I(x)与一些先验知识,通过优化算法,得到均匀的图像I'(x).通常是先获得偏场B(x)之后,通过下式得到校正图像:
| $ I'\left( x \right) = I\left( x \right)/B\left( x \right) $ | (3) |
基于分割的回溯性校正方法将灰度不均匀校正与图像分割两者结合起来,或者迭代交替处理这两个过程、或者两者同时进行约束,共同促进最终得到好的灰度不均匀校正图像和分割结果.
2009年,Li等人[15]提出了CLIC算法.它是基于FCM方法的图像分割与灰度校正方法,在FCM中加入了偏场连续性约束,能同时对图像进行组织分割和偏场估计.CLIC算法的基本思想是:对于图像中某个点x,其邻域中的像素I(y),需要满足一定的聚类准则.其中聚类中心用B(x)ci代替,B(x)为像素点x处的不均匀偏场大小,ci为某种组织的理论灰度值.如果位于y位置的像素I(y)距离邻域中心像素B(x)ci距离较近,那么该像素对邻域中心像素的聚类影响应该较大;反之则较小.因此,需要引入一个权重来控制邻域内每个像素点对聚类的影响.作者把这种约束处理称为CLIC,其定义的聚类准则函数如下:
| $ \varepsilon \left( {U,c,B} \right) = \sum\nolimits_{i = 1}^N {\int {u_i^q\left( y \right)K\left( {x - y} \right){{\left| {I\left( y \right) - B\left( x \right){c_i}} \right|}^2}{\rm{d}}y} } $ | (4) |
其中,I代表图像;B代表偏场;N表示迭代次数;c=(c1, c2, ...),代表组织的灰度值;uiq是组织区域Ωi的隶属函数,定义为:
| $ u_i^q\left( x \right) = \left\{ \begin{array}{l} 1,x \in {\mathit{\Omega }_i}\\ 0,x \notin {\mathit{\Omega }_i} \end{array} \right. $ | (5) |
K是截断高斯窗函数,定义如下:
| $ K\left( x \right) = \left\{ \begin{array}{l} \frac{1}{a}{{\rm{e}}^{\frac{{{{\left| x \right|}^2}}}{{2{\sigma ^2}}}}},\left| x \right| \le r\\ 0,\;\;\;\;\;\;\;{\rm{otherwise}} \end{array} \right. $ | (6) |
其中a是归一化常数,使得∫K(x)dx=1;σ表示高斯函数所用的标准差;r表示高斯函数的半径.最终得到的求解分割和灰度不均匀校正问题的能量函数如下:
| $ F\left( {U,c,B} \right) = \int {\varepsilon \left( {U,c,B} \right){\rm{d}}x} + v\left| C \right| $ | (7) |
其中|C|表示分割轮廓C的长度,v是权重常数.
在文献[16]中,Li等人用水平集方法[17]求解CLIC,得到其水平集形式为:
| $ \begin{array}{l} F\left( {\phi ,c,B} \right) = \sum\nolimits_i {{\lambda _i}} \int {\int {K\left( {x - y} \right){{\left| {I\left( y \right) - B\left( x \right){c_i}} \right|}^2}{M_i}\left[ {\phi \left( y \right)} \right]{\rm{d}}y{\rm{d}}x} } \\ + v\int {\left| {\nabla {H_\varepsilon }\left[ {\phi \left( x \right)} \right]} \right|{\rm{d}}x + \mu \int {\frac{1}{2}{{\left[ {\left| {\nabla \phi \left( x \right)} \right| - 1} \right]}^2}{\rm{d}}x} } \end{array} $ | (8) |
其中ϕ是水平集函数.(8) 式第1项是(4) 式的水平集形式,第2项是对分割轮廓的约束,第3项是水平集函数的正则项,λ、v、μ是对应项的权重常数.Mi是对应于区域Ωi的成员函数,用来区分不同组织区域.Hε是光滑Heaviside函数:
| $ {H_\varepsilon }\left( x \right) = \frac{1}{2}\left[ {1 + \frac{2}{\pi }\arctan \left( {\frac{x}{\varepsilon }} \right)} \right] $ | (9) |
其中ε是用来调整光滑Heaviside函数的光滑程度的一个常数参数.
算法求解公式详见附录A.
1.3 分裂布雷格曼迭代算法布雷格曼迭代是Bregman[18]于1967年提出的,最初用于泛函分析中寻找凸泛函的极值.2005年,Osher等人[19]首次将布雷格曼迭代应用于图像处理中的全变分去噪问题中.之后,布雷格曼迭代也被广泛用于处理各类优化问题,例如用于压缩感知问题中[20].
在布雷格曼迭代算法的基础上,Goldstein和Osher提出分裂布雷格曼方法,用于解决l1正则问题的一般形式(算法具体形式见附录B).分裂布雷格曼方法已经被用于更加有效地解决各类图像处理问题,例如用于图像去噪和压缩感知问题[21, 22]、结合各种分割模型用于解决图像分割问题[23, 24].分裂布雷格曼方法可以快速并且更好地解决l1正则化问题.相较于传统的求解l1正则化问题的方法,分裂布雷格曼方法的优点是不需要正则化、连续性和不等式等约束条件,因此可以非常快速地收敛.2014年,Yang等人[25]将分裂布雷格曼算法用于不均匀图像多相分割模型中,处理图像分割问题,其能量函数结合了局部灰度信息、全局灰度信息和边缘信息,分裂布雷格曼算法的引入使其计算速度快于CLIC算法.
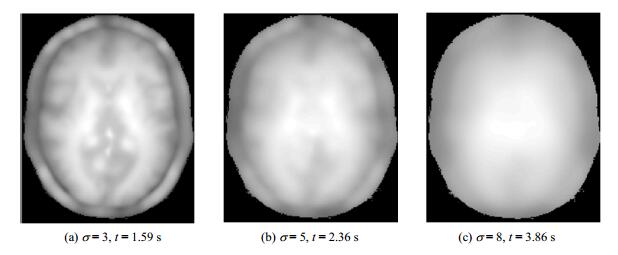
1.4 结合分裂布雷格曼迭代的CLIC模型CLIC模型只约束图像局部信息,用于偏场校正时,获得的偏场容易带有细节信息.截断高斯窗函数半径r越小,偏场中包含的图像结构细节信息越多(如图 1所示).使用较大半径的窗函数可以改善这一问题,获得的偏场会更加光滑,但使用的窗函数半径越大,图像重建所需时间越长(见图 1中统计的运行时间).
|
图 1 不同半径(r)的高斯窗函数下,CLIC计算得到的偏场.σ表示高斯窗函数所用的标准差,同时也确定了窗函数的大小(边长h=4σ +1,半径r=h/2).t为5次独立实验统计得到的平均时间,每组实验外循环次数为40,内循环次数为1 Figure 1 Bias field obtained by CLIC in different radiuses (r) of the Gaussian windows function. σ is the standard deviation of the Gaussian kernel used. It also determines the size of the window function, which should be set as (4σ +1). t was the average time used of 5 experiments using CLIC. The outer loop count of CLIC was 40, while the inner loop count was 1 |
针对这个问题,我们提出结合分裂布雷格曼迭代算法来降低采用较大半径的高斯窗函数时的时间消耗.同时,我们将边缘检测函数整合到CLIC模型的能量函数中,使得算法进行分割时,更容易检测到组织边缘.算法推导过程详见附录C.
我们的算法(记为SpB-CLIC)流程描述如下:
| 输入:ϕ0, I(x), while ║ϕn+1-ϕn║>ε do 根据公式(A5) 计算cn+1. 利用分裂布雷格曼迭代算法求解ϕn+1. 根据公式(A4) 计算偏场Bn+1. End 计算校正后的图像,I'=I/B; |
其中分裂布雷格曼迭代算法包含如下的内循环:
| 输入:ϕ0n=ϕn,d0n=b0n=0 利用Gauss-Seidel方法求解ϕk+1n. 利用公式(C10) 计算dk+1n. 根据公式(C8) 计算布雷格曼变量bk+1n. (此处的下标表示内循环迭代到第几步,上标表示外循环迭代) |
2 实验结果与讨论 2.1 模拟磁共振图像数据处理 2.1.1 实验数据及参数
我们从BrainWeb上下载到无噪声、带100%不均匀度的MRI脑图[图 2(a)]作为模拟数据,图像大小为217×181,并下载了无噪声、均匀的磁共振图像[图 2(d)]作为金标准图像用于分析.SpB-CLIC的参数为:ε=1,ρ=0.1,λ=100,λ1 =λ2=λ3=λ4 = 1.2,ε=0.4,σ=10,高斯窗边长为h = 4σ + 1 = 41.对照组为文献[16]中所用的CLIC方法,其中的水平集函数用有限差分方法求解,所用参数为ε = 1,μ = 1,v = 1,步长取0.1.

|
图 2 SpB-CLIC与CLIC灰度校正结果的比较. (a)带100%灰度不均匀的原始图像; (b)与(e) SpB-CLIC校正后的图像与偏场;(c)与(f) CLIC校正后的图像与偏场; (d)金标准图像 Figure 2 Comparison of SpB-CLIC and CLIC. (a) Image with bias field; (b) and (e) Corrected image and bias field with SpB-CLIC; (c) and (f) Corrected image and bias field with CLIC; (d) Gold standard MRI image |
为了定性地评价图像校正的质量,我们使用联合变异系数(coefficient of joint variation, CJV)来检测校正后图像的均匀性.两种组织A、B间的CJV定义如下[26]:
| $ CJV\left( {{\rm{A}},{\rm{B}}} \right) = \left[ {\sigma \left( {\rm{A}} \right) + \sigma \left( {\rm{B}} \right)} \right]/\left| {\mu \left( {\rm{A}} \right) - \mu \left( {\rm{B}} \right)} \right| $ | (10) |
其中,σ表示该组织的标准差,μ代表该组织的平均值.从定义上可以看出,图像灰度越均匀,其两种组织求得的CJV越小.
2.1.2 实验结果与分析图像校正效果如图 2所示,图像的直方图比较如图 3所示.从直方图上可以看出,受不均匀偏场污染的图像(品红色点划线),直方图上几乎看不出明显的峰,表明灰度均匀性差.经过SpB-CLIC(红色实线)或CLIC(蓝色虚线)校正后的图像,出现明显的峰,且峰的位置都较接近金标准图像(绿色点线)中峰的分布,这说明校正后图像灰度均匀性得到改善.实验结果表明,分裂布雷格曼迭代算法能有效结合到CLIC中,用于校正磁共振图像灰度不均匀.

|
图 3 SpB-CLIC和CLIC校正后图像的直方图比较(直方图不包含背景区域) Figure 3 Histogram comparison of raw image with of images corrected with SpB-CLIC, CLIC and gold standard image (pixels in the background is not included) |
用上面实验数据,在相同参数下,重复5次实验,取平均值,统计得到实验的数值结果如表 1所示:
| 表 1 SpB-CLIC和CLIC重建结果比较 Table 1 Comparison of SpB-CLIC and CLIC method |
如前面所述,图像的灰度均匀性越好,CJV越小.原始图像由于受到偏场的污染,其CJV比金标准图像的要大,而校正过后的图像CJV都变小.SpB-CLIC校正后的图像CJV要比CLIC算法的要小,表明其校正效果更好.需要注意的是,一般校正后图像的CJV与金标准的相比仍偏高,这是因为磁共振图像中存在部分容积效应,偏离一般的灰度校正方法所假设的模型.从表 1可看出,在CJV及运算时间上,SpB-CLIC略优于CLIC.
对照组中μ = 1,这项参数对应于水平集正则项.而SpB-CLIC中相当于μ = 0.实验结果表明,水平集方法在不用水平集正则项约束的情况下,也能得到好的演化结果,这与附录C的分析一致.
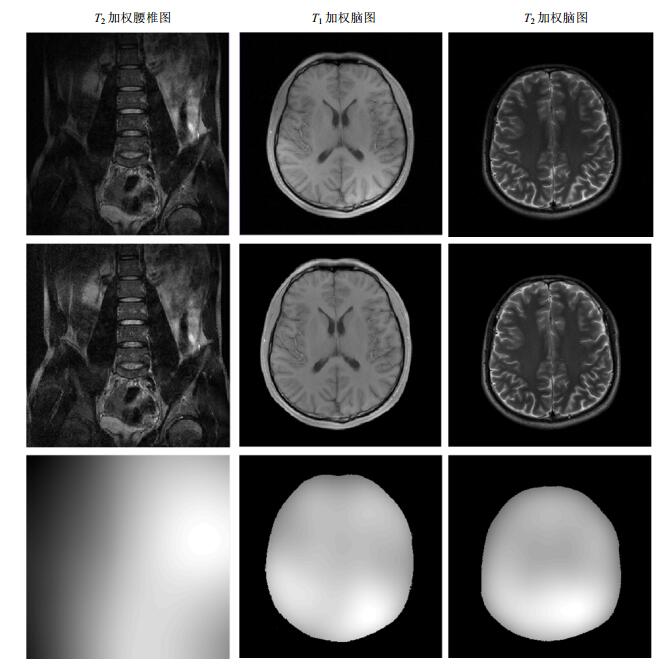
2.2 真实磁共振图像数据处理 2.2.1 实验数据及参数第2组实验中,我们将算法用于处理真实磁共振图像,分别为T2加权腰椎图、T1加权脑图和T2加权脑图(如图 4第1行所示).第一列T2加权腰椎数据来源于上海卡勒幅磁共振技术有限公司的Sapphire 1.5 T超导MRI系统,所用扫描序列为fast spin echo(FSE)快速自旋回波序列,接收线圈为4通道体线圈,扫描矩阵(matrix)= 256×256,视野(FOV)= 300×300 mm2,脉冲序列重复间隔时间(TR)= 3 500 ms,回波时间(TE)= 95 ms,Flip Angle = 90˚.第2列T1加权脑图数据和第3列中的T2加权脑图数据来源于西门子3 T Trio TimMRI系统.其中T1加权脑图采集时所用扫描序列为fast low angle shot(FLASH)快速小角度激发序列,接收线圈为12通道头线圈,matrix = 320×320,FOV = 220×220 mm2,TR = 250 ms,TE = 2.46 ms,Flip Angle = 70˚;T2加权脑图采集时所用扫描序列为turbo spin echo(TSE)快速自旋回波序列,接收线圈为12通道头线圈,matrix = 640×640,FOV = 220×220 mm2,TR = 6000 ms,TE = 93 ms,Flip Angle = 120°.
|
图 4 SpB-CLIC用于校正真实磁共振图像.第1行是原始图像;第2行是校正后的图像;第3行是算法计算得到的偏场,其中第2列、第3列的只显示了感兴趣区域(region of interest, ROI)内的偏场 Figure 4 Results of SpB-CLIC applied to correct the intensity inhomogeneity for real MR images. Top: original images; Middle: corrected images; Bottom: bias fields in regions of interest |
实验中,算法的外循环次数为10,内循环次数为5,其他参数为ρ = 0.1,λ = 100,λ1=λ2=λ3 = λ4= 1.2,第1列数据(图像大小为256×256)中σ = 50,第2列数据(图像大小为320×320)中σ =20, 第3列数据(图像大小为640×640)中σ = 50.
2.2.2 实验结果与分析实验结果如图 4所示.
从图中可以看出,SpB-CLIC校正过后的图像(第2行)灰度均匀性有明显提高,算法计算到的偏场(第3行)较好反映了原图(第1行)中的灰度不均匀.从这些图中可以看出,SpB-CLIC对真实磁共振图像的灰度不均匀校正也有较好的效果.
3 结论本文提出了一种基于分裂布雷格曼迭代和CLIC模型的灰度校正算法——SpB-CLIC.该算法结合了CLIC模型、边缘检测函数和分裂布雷格曼迭代方法,既保留了CLIC模型应用于不均匀图像的分割效果,又充分利用了图像边缘信息便于搜索到组织边界,而分裂布雷格曼迭代的引入则减少了在保证偏场光滑情况下所需要的计算时间.实验结果表明,该算法处理后图像的灰度均匀性,在视觉效果和数据统计上都有提高.
附录A:CLIC算法能量函数的解[16]
CLIC算法所要求解的能量函数[(8) 式]可通过交替迭代过程来得到最小值:每次迭代中,先固定两个变量,最小化另一个变量.
对于给定的B和c,ϕ可以通过标准梯度下降法来得到最小值:
| $ \frac{{\partial {\phi _k}}}{{\partial t}} = - \sum\nolimits_{i = 1}^N {{\lambda _i}\frac{{\partial {M_i}\left( \phi \right)}}{{\partial {\phi _i}}}{e_i}} + v\delta \left( {{\phi _k}} \right)div\left( {\frac{{\nabla {\phi _k}}}{{\left| {\nabla {\phi _k}} \right|}}} \right) + \mu \left[ {{\nabla ^2}\phi - div\left( {\frac{{\nabla {\phi _k}}}{{\left| {\nabla {\phi _k}} \right|}}} \right)} \right] $ | (A1) |
其中
| $ {e_i}\left( x \right) = \int {K\left( {y - x} \right){{\left| {I\left( x \right) - B\left( y \right){c_i}} \right|}^2}} {\rm{d}}y $ | (A2) |
| $ \delta \left( {{\phi _k}} \right) = H'\left( {{\phi _k}} \right) $ | (A3) |
给定c和ϕ,B可以通过下式求解:
| $ B = \frac{{\left( {I\sum\nolimits_{i = 1}^N {{c_i}{M_i}} } \right) \times K}}{{\left( {I\sum\nolimits_{i = 1}^N {c_i^2{M_i}} } \right) \times K}} $ | (A4) |
给定B和ϕ,c可以通过下式求解:
| $ {c_i} = \frac{{\int {\left( {B \times K} \right)I{M_i}{\rm{d}}y} }}{{\int {\left( {{B^2} \times K} \right)I{M_i}{\rm{d}}y} }} $ | (A5) |
附录B:分裂布雷格曼迭代算法[21]
Goldstein和Osher提出的分裂布雷格曼迭代算法,可以用于求解如下l1正则问题:
| $ {\min _u}{\left| {\mathit{\Phi }\left( u \right)} \right|_1} + H\left( u \right) $ | (B1) |
其中Φ(u)和H(u)都是凸函数,且H(u)可微.
分裂布雷格曼迭代方法的中心思想是将(B1) 式中的l1项分离出来,通过引入一个辅助变量d,上式转化为如下的约束最小化问题:
| $ {\min _{u,d}}{\left| d \right|_1} + H\left( u \right)\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;d = \mathit{\Phi }\left( u \right) $ | (B2) |
然后采用布雷格曼迭代方法求解该约束优化问题,得到下面的迭代求解公式:
| $ {u^{k + 1}},{d^{k + 1}} = \arg {\min _{u,d}}{\left| d \right|_1} + H\left( u \right)\; + \frac{\lambda }{2}{\left\| {d - \mathit{\Phi }\left( u \right) - {b^k}} \right\|^2} $ | (B3) |
| $ {b^{k + 1}} = {b^k} + \left[ {\mathit{\Phi }\left( {{u^{k + 1}}} \right) - {d^{k + 1}}} \right] $ | (B4) |
其中(B3) 式可以通过交替最小化下面两式求解:
| $ {u^{k + 1}} = \arg {\min _u}H\left( u \right)\; + \frac{\lambda }{2}{\left\| {{d^k} - \mathit{\Phi }\left( u \right) - {b^k}} \right\|^2} $ | (B5) |
| $ {d^{k + 1}} = \arg {\min _d}{\left| d \right|_1}\; + \frac{\lambda }{2}{\left\| {d - \mathit{\Phi }\left( {{u^{k + 1}}} \right) - {b^k}} \right\|^2} $ | (B6) |
附录C:结合分裂布雷格曼迭代的CLIC模型算法推导
为了使CLIC灰度校正模型的能量函数能用分裂布雷格曼迭代方法求解,我们需要对CLIC模型的能量函数做一些调整.(8) 式中的最后一项称为水平集正则项,其作用是保证水平集函数在零水平集附近是一个近似的符号距离函数[16, 27].文献[28]中指出,这一项对迫使活动轮廓朝物体边缘演变不起作用,在分割模型中并非是必需的,同样对我们的灰度校正模型来说也是如此.因此我们可以先不考虑(8) 式中最后一项水平集正则项.相当于(A1) 式中,μ = 0,此时的能量函数仍然符合分割模型(7) 式.由于参数表示的是相对权重,我们可以取定v = 1,得到如下简化模型:
| $ \frac{{\partial {\phi _k}}}{{\partial t}} = \delta \left( {{\phi _k}} \right)\left[ {div\left( {\frac{{\nabla {\phi _k}}}{{\left| {\nabla {\phi _k}} \right|}}} \right) - S} \right] $ | (C1) |
其中,
| $ S = \frac{1}{{\delta \left( {{\phi _k}} \right)}}\sum\nolimits_{i = 1}^N {\frac{{{\lambda _i}\partial {M_i}\left( \phi \right)}}{{\partial {\phi _k}}}{e_i}} $ | (C2) |
(C1) 式也是最小化下式所能得到的梯度下降法形式:
| $ {F_k}\left( \phi \right) = \left| {\nabla \phi } \right| + \left\langle {\phi ,S} \right\rangle ,{a_0} < \phi < {b_0} $ | (C3) |
即(C3) 式与(C1) 式同解.为了利用充分利用图像全局信息,使得算法能更快找到最优解,我们在上式的TV项中加入边缘检测信息,变成加权TV范数[29]:
| $ T{V_g}\left( \phi \right) = {\left| {\nabla \phi } \right|_g} = \int {g\left[ {\nabla I\left( x \right)} \right]\left| {\nabla \phi \left( x \right)} \right|{\rm{d}}x} $ | (C4) |
函数g为边缘检测函数:
| $ g\left[ {\left| {\nabla I\left( x \right)} \right|} \right] = \frac{1}{{1 + \rho {{\left| {\nabla G \times I\left( x \right)} \right|}^2}}} $ | (C5) |
其中∇G×I(x)表示高斯滤波后的图像的梯度.
此时能量函数变为:
| $ {F_k}\left( \phi \right) = \min {\left| {\nabla \phi } \right|_g} + \left\langle {\phi ,S} \right\rangle ,{a_0} < \phi < {b_0} $ | (C6) |
用分裂布雷格曼迭代求解上式,得到如下的方程:
| $ \left( {\phi _k^{n + 1},{d^{n + 1}}} \right) = \arg {\min _{\phi \in \left[ { - 2,2} \right],d}}{\left| d \right|_g} + \left\langle {\phi ,S} \right\rangle + \frac{\gamma }{2}\left\| {d - \nabla \phi - {b^n}} \right\|_2^2 $ | (C7) |
| $ {b^{n + 1}} = {b^n} + \nabla {\phi ^{n + 1}} - {d^{n + 1}} $ | (C8) |
固定d,ϕ的最优解可以通过下式获得:
| $ \Delta \phi = \frac{s}{\gamma } + \nabla \left( {{d^n} - {b^n}} \right) $ | (C9) |
上式可以很容易用Gauss-Seidel方法求解得出ϕn+1.
固定ϕ,d可以通过软阈值算法得到:
| $ {d^{n + 1}} = shrin{k_g}\left( {{b^n} + \nabla {\phi ^{n + 1}},\frac{1}{\gamma }} \right) = shrink\left( {{b^n} + \nabla {\phi ^{n + 1}},\frac{g}{\gamma }} \right) $ | (C10) |
其中
| $ shrink\left( {x,\lambda } \right) = \frac{x}{{\left| x \right|}}\max \left( {\left| x \right| - \lambda ,0} \right) $ | (C11) |
| [1] | HAACKE E M, BROWN R W, THOMPSON M R, et al. Magnetic resonance imaging:Physical principles and sequence design[M]. New Jersey: John Wiley & Sons, 2014. |
| [2] | 周康荣, 陈祖望. 体部磁共振成像[M]. 上海: 上海医科大学出版社, 2000. |
| [3] | VOVK U, PERNUS F, LIKAR B. A review of methods for correction of intensity inhomogeneity in MRI[J]. IEEE T Med Imaging, 2007, 26(3): 405-421. DOI: 10.1109/TMI.2006.891486. |
| [4] | DAWANT B M, ZIJDENBOS A P, MARGOLIN R A. Correction of intensity variations in MR images for computer-aided tissue classification[J]. IEEE T Med Imaging, 1993, 12(4): 770-781. DOI: 10.1109/42.251128. |
| [5] | ERNST T, KREIS R, ROSS B D. Absolute quantitation of water and metabolites in the human brain. Ⅰ. compartments and water[J]. J Magn Reson, 1993, 102(1): 1-8. |
| [6] | PRUESSMANN K P, WEIGER M, SCHEIDEGGER M B, et al. SENSE:sensitivity encoding for fast MRI[J]. Magn Reson Med, 1999, 42(5): 952-962. DOI: 10.1002/(ISSN)1522-2594. |
| [7] | MIHARA H, IRIGUCHI N, UENO S. A method of RF inhomogeneity correction in MR imaging[J]. Magn Reson Mater Phys, 1998, 7(2): 115-120. DOI: 10.1007/BF02592235. |
| [8] | HOU Z J. A review on MR image intensity inhomogeneity correction[J]. Int J Biomed Imaging, 2006, 2006(49515): 1-11. |
| [9] | BALAFAR M A, RAMLI A R, MASHOHOR S. A new method for MR grayscale inhomogeneity correction[J]. ArtifIntell Rev, 2010, 34(2): 195-204. |
| [10] | SLED J G, ZIJDENBOS A P, EVANS A C. A nonparametric method for automatic correction of intensity nonuniformity in MRI data[J]. IEEE T Med Imaging, 1998, 17(1): 87-97. DOI: 10.1109/42.668698. |
| [11] | ZHUGE Y, UDUPA J K, LIU J, et al. Image background inhomogeneity correction in MRI via intensity standardization[J]. Comput Med Imag Grap, 2009, 33(1): 7-16. DOI: 10.1016/j.compmedimag.2008.09.004. |
| [12] | GARCIA-SEBASTIAN M, FERN-NDEZ E, GRANA M, et al. A parametric gradient descent MRI intensity inhomogeneity correction algorithm[J]. Pattern Recogn Lett, 2007, 28(13): 1657-1666. DOI: 10.1016/j.patrec.2007.04.016. |
| [13] | MAKSIMOVIC R, STANNKOVIC S, MILOVANOVIC D, et al. Computed tomography image analyzer:Segmentation applying active contour models——"snakes"[J]. Stud Health Technol Inform, 1999, 68: 395-399. |
| [14] | ZHANG S, SHE L H, WANG H Y, et al. Brain MR image segmentation and bias field estimation using coherent local and non-local spatial constraints[C]. Guiyang:Proceedings of the 25th Chinese Control and Decision Conference (CCDC), 2013. |
| [15] | LI C M, XU C Y, ANDERSON A W, et al. MRI tissue classification and bias field estimation based on coherent local intensity clustering:A unified energy minimization framework[J]. Inf Process Med Imaging, 2009, 21(2): 88-99. |
| [16] | LI C M, HUANG R, DING Z H, et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J]. IEEE T Image Process, 2011, 20(7): 2007-2016. DOI: 10.1109/TIP.2011.2146190. |
| [17] | OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed:Algorithms based on Hamilton-Jacobi formulations[J]. J Comput Phys, 1988, 79(1): 12-49. DOI: 10.1016/0021-9991(88)90002-2. |
| [18] | BREGMAN L M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming[J]. USSR Comput Math Math Phys, 1967, 7: 200-217. |
| [19] | OSHER S, BURGER M, GOLDFARB D, et al. An iterative regularization method for total variation-based image restoration[J]. Multiscale Model Sim, 2006, 4(2): 460-489. |
| [20] | YIN W T, OSHER S, GOLDFARB D, et al. Bregman iterative algorithms for l1-minimization with applications to compressed sensing[J]. SIAM J Imaging Sci, 2008, 1(1): 143-168. DOI: 10.1137/070703983. |
| [21] | GOLDSTEIN T, OSHER S. The split bregman method for l1-regularized problems[J]. Siam J Imaging Sci, 2009, 2(2): 323-343. DOI: 10.1137/080725891. |
| [22] | SMITH D S, GORE J C, YANKEELOV T E, et al. Real-time compressive sensing MRI reconstruction using GPU computing and split Bregman methods[J]. Int J Biomed Imaging, 2012: 1-6. |
| [23] | YANG Y Y, LI C M, KAO C Y, et al. Split Bregman method for minimization of region-scalable fitting energy for image segmentation[M]. Berlin: Springer Berlin Heidelberg, 2010. |
| [24] | GOLDSTEIN T, BRESSON X, OSHER S. Geometric applications of the split Bregman method:Segmentation and surface reconstruction[J]. J Sci Comput, 2010, 45(1): 272-293. |
| [25] | YANG Y Y, ZHAO Y, WU B Y. Split Bregman method for minimization of fast multiphase image segmentation model for inhomogeneous images[J]. J Optimiz Theory App, 2014, 166(1): 285-305. |
| [26] | LIKAR B, VIERGEVER M A, PERNUS F. Retrospective correction of MR intensity inhomogeneity by information minimization[J]. IEEE T Med Imaging, 2001, 20(12): 1398-1410. DOI: 10.1109/42.974934. |
| [27] | LI C M, XU C Y, GUI C F, et al. Level set evolution without re-initialization:A new variational formulation[J]. CVPR'05, 2005. DOI: 10.1109/CVPR.2005.213. |
| [28] | 杨云云. 基于Split Bregman方法的快速图像分割模型的研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. |
| [29] | BRESSON X, ESEDOGLU S, VANDERGHEYNST P, et al. Fast global minimization of the active contour/snake model[J]. J Math Imaging Vis, 2007, 28(2): 151-167. DOI: 10.1007/s10851-007-0002-0. |
 2017, Vol. 34
2017, Vol. 34 
