文章信息
- 邓峰, 肖立志, 陶冶, 耿东士, 王梦颖
- DENG Feng, XIAO Li-zhi, TAO Ye, GENG Dong-shi, WANG Meng-ying
- 流动速度对核磁共振在线测量的影响及校正
- Low-Field NMR Flowing Fluid Measurement: The Effects of Flow Rate and Corrections
- 波谱学杂志, 2017, 34(1): 78-86
- Chinese Journal of Magnetic Resonance, 2017, 34(1): 78-86
- http://dx.doi.org/10.11938/cjmr20170110
-
文章历史
收稿日期: 2016-07-29
收修改稿日期: 2017-01-05


DOI:10.11938/cjmr20170110
2. 中国石油大学(北京), 油气资源与探测国家重点实验室, 北京 102249
2. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China
核磁共振(NMR)在线测量作为一种高效、无损的探测技术,可广泛应用于物理、化学、生物、医学、农业、石油和地质等多种学科领域中,对诸如流体、气体、孔隙介质等样品进行在线检测.传统的静止测量,例如传统的NMR实验室内测量仪器、测量方法和解释方法,均无法直接用于在线NMR测量,NMR在线检测技术面临更多挑战.
NMR在线测量,即探头和被测样品在保持相对运动的条件下进行NMR射频脉冲发射和回波信号接收.在线测量包含两种模式:一种模式是样品保持静态而探头运动,例如石油测井[1]、建筑物表层材料扫描[2]和土壤湿度扫描[3]等;另一种模式是探头保持静止而样品运动,例如输送管道中流动流体检测[4, 5]、流动血液的检测[6]等.在第一种模式下,运动对NMR在线测量影响的实质是在NMR测量过程中,运动速度本身对样品磁化时间和回波采集时间均会造成限制,带来样品不能完全磁化和采集信号丢失两方面的影响.且相对运动速度越快,影响越明显.在第二种模式下,若样品呈固态或在测量过程中本身结构无变化,则运动影响与第一种测量模式没有本质区别.但如果样品本身是流动的流体,则运动影响不光体现在相对速度上,还包括流动状态下样品本身的变化.
最早关注运动对NMR测井影响的Akkurt在其著作[7]中对NMR测井过程作了详细的数学建模描述,分析各个影响因素的同时提出了一种利用经验模板对测量结果进行校正的运动校正方法;而后Edwards[8]、Menger[9]、刘双惠[10]等人分别从仪器设计、测井速度、弛豫时间和纵向分辨率等不同角度研究了运动对NMR在线测量的影响,提出了运动校正的必要性,但均未提及具体的校正方法;2012年,Chanh等人[11]针对运动对横向弛豫时间(T2)的影响提出了一套回波串校正方法,校正结果准确,且起到了提高回波信号信噪比(SNR)的作用,但由于并未同时考虑运动对纵向弛豫时间(T1)的影响,所以这种校正方法的适用范围具有局限性.我们早前的工作完成了第一种测量模式下的运动影响因素分析并提出校正方法[12],本文将在此基础上重点研究流动状态对NMR在线测量的影响,并在量化分析的基础上进一步提出流动校正方法.
1 理论流动流体NMR测量与静止流体NMR测量的差别主要体现在两个方面:一是静止状态下流体分子只在小范围内进行布朗运动,而流动状态下,布朗运动几乎被流动所掩,如图 1(a)所示;二是静止状态下,样品的磁化时间和回波采集时间可以根据需要人为设置,而流动状态下,流体快速通过探头,磁化时间和回波采集时间均受流速的限制.

|
| 图 1 不同流态对NMR在线测量影响的示意图. (a) 低场在线NMR测量示意图;(b) 黏塑性流体的流态转变过程示意图;(c) 一次NMR脉冲序列测量期间探测区域内流体的移动情况 Fig. 1 Flow patterns and the flowing effects on online NMR measurements. (a) Online low-field NMR measurement schematic, (b) Viscoplastic fluid flow state transition schematic, (c) Fluid movement during a single pulse sequence measurement |
圆管内流体由于自身特性的差异和所受圆管两侧压差的大小,在流动过程中呈现不同的流态[13],包括塞流、层流、过渡流和紊流.对于非牛顿流体而言,随着压差升高,由塞流直到形成紊流前的所有流动状态均统称为结构流.结构流又呈现不同的流变模式,包括宾汉(Bingham)模式[14]、幂律(Ostwald-de Waele power law)模式、卡森(Casson)模式[15]和赫-巴(Herschel-Bulkley)模式[16]等,如图 1(b)所示.本文的研究对象是不同流变模式下流体在圆管中的轴向结构流.
在塞流状态下,流动对NMR在线测量的影响主要是流速的影响,其影响因素和前面提到的第一种在线测量模式类似,这时也可以看成样品是静止的而探头在连续运动.以Carr-Purcell-Meiboom-Gill(CPMG)脉冲序列的测量为例,假设流体是一种由i种组分组成的混和流体,在磁化过程和回波采集过程中的信号幅值可由Bloch方程[17]推导如下:
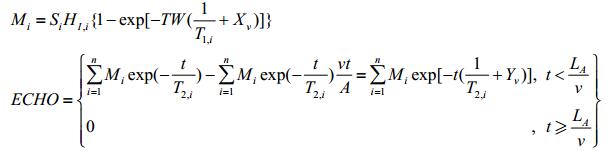
|
(1) |
其中,Mi表示磁化过程结束时流体样品中第i种组分的磁化矢量,ECHO是采集得到的回波信号幅值,Si是第i种组分的饱和度,HI, i是第i种组分的含氢指数,TW是磁化时间,T1, i是第i种组分的纵向弛豫时间,T2, i是第i种组分的横向弛豫时间,LA是天线长度,v是流速,t是回波采集时间,Xv和Yv分别表示流速对磁化过程和回波采集过程的影响.
以牛顿流体圆管层流为分析对象,以圆形管流为例,流体在泵压的驱动下流动,通过力平衡分析,得到如下关系式:
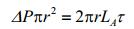
|
(2) |
其中,ΔP是流体在探头探测区域两端的压力差,r取值在0~R(管道半径)之间,τ是剪切应力,其表达式为:
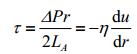
|
(3) |
η是流体粘度,u是流体的平均流速,其表达式为:
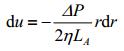
|
(4) |
可以推导出层流状态下流体流速在管道横截面上的分布函数为:
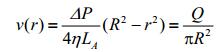
|
(5) |
Q是流量.其他几种流态下的流速分布函数如下:
宾汉模式:
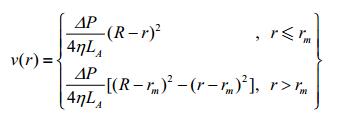
|
(6) |
其中,rm是流核半径;
幂律模式:

|
(7) |
其中,K是粘度系数,n是流性指数;
卡森模式:
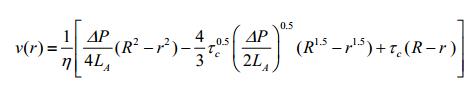
|
(8) |
其中,τc是卡森屈服值;
赫-巴模式:

|
(9) |
以CPMG脉冲序列为例,NMR测量包含样品磁化和回波采集两个过程.在样品磁化过程中[如图 1(a)所示],流体进入探头后先流经LM段磁体,这段磁体会对流体进行预磁化.如果流体流速很快,在磁化未完成(TW < 4T1)就已流入天线探测区域,则会产生“磁化不充分”现象.在这种情况下,Xv的表达式如下:

|
(10) |
其结果是导致回波串的首幅值偏低.但有时也会出现“过度磁化”的现象,这里指人为设定的TW < 4T1的一些特殊测量模式下,例如双TW测量和二维T1-T2测量.在这种情况下,天线所采集到的回波幅度实际上是经磁体磁化后进入天线的样品和天线内正在进行磁化的样品两部分磁化矢量的和:
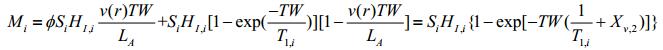
|
(11) |
可以得到Xv, 2的表达式如下:

|
(12) |
图 1(c)给出了一次NMR脉冲序列的测量期间,流体的移动情况.在流体经过磁化进入到天线区域后,首个90˚脉冲发射时,整个天线内流体的原子核磁化矢量方向都被扳转,随后发射一系列的180˚脉冲并进行回波信号的采集,随着回波采集时间的推移,一部分已被扳转的流体流出了天线区域,而另一部分未被扳转的流体流入了探测区域,这两部分流体均无法产生回波信号,这就发生了信号损失的情况,且回波采集时间越长,信号损失量越大.在明确了流态,得到流速分布v(r) 后,就不难推导出Yv的表达式:

|
(13) |
Xv的影响主要体现在回波串的首幅值上,在采用同样的测量参数对同一流体样品进行NMR在线测量时,Xv, 1会导致流动状态下所采集到的回波串的首幅值低于静止状态,Xv, 2则相反;Yv额外增加了回波串的衰减速度.
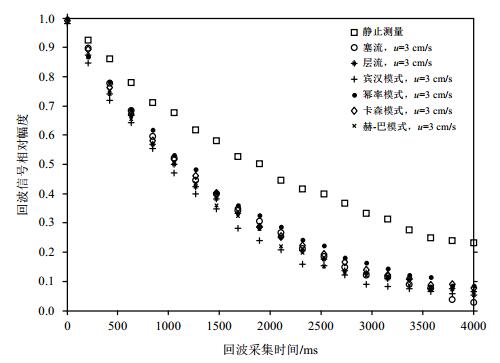
由于不同流态的速度分布函数各不相同,因此对NMR在线测量的影响也各不相同.图 2所示是数值模拟不同流态下的流体在相同流量的前提下采集得到的CPMG回波串数据.设定参数如下:圆管内径(R)=1 cm,流量(Q)=0.75 cm3/s,SNR=100,T1=3 s,T2=2 500 ms,TW=12 000 ms,回波间隔(TE)=4 ms,回波个数(N)=1 000.数值模拟结果表明:一方面由于受流动状态的影响,流动状态下回波信号的衰减速率要明显快于静止状态;另一方面,几种流态下信号衰减的速率差别不大,因此在进行流动影响实验研究时,选用单一牛顿流体作为样品.此外,由于T1和T2都比较大的流体(例如纯净水),需要较长的磁化时间和回波采集时间,受流动的影响也更明显.
|
| 图 2 数值模拟不同流态下,流动对NMR在线测量的影响 Fig. 2 Flowing effect on online NMR measurement with different flow patterns |
在量化分析了流动对NMR在线测量的影响以后,就可以直接通过数学方法校正回波串数据,以达到控制乃至消除流动影响的目的.磁化过程中,流动的影响主要体现在对回波串首幅值的影响,在进行磁化过程校正(Xv校正)时,可将采集的回波串数据乘以校正因子Cx:

|
(14) |
可根据实际所选用的测量模式选择Xv是选用Xv, 1还是Xv, 2的表达式.需要注意的是,(14) 式中的T1是流体样品的真实T1分布,这是需要通过测量实现的,在实际应用中,T1可于通过测量自由感应衰减(FID)信号得到.由于一次测量时间短,T1的测量不会受到流动状态的影响,故可在开展CPMG脉冲序列测量前,先完成一次T1分布的测量.
完成对回波串数据的磁化过程校正后,在回波采集过程中Yv的影响也同样可通过数据校正消除.流动对磁化过程的影响是在流体流入天线区域时“一次性”发生的,因此Xv的影响主要是针对回波串的首幅值;但流动对回波采集过程的影响是随时间推移而变化的,因此Yv对每个回波的影响各不相同.这里所采用的回波串数据校正方法包括如下4个步骤:(ⅰ)对采集到的原始回波串数据进行奇异值分解(SVD);(ⅱ)将SVD处理后的回波串数据乘以校正因子Cy:
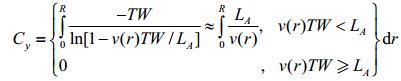
|
(15) |
(ⅲ)将乘以校正因子前后的回波串数据做差,得到一组差值数据Er;(ⅳ)从采集得到的原始回波串数据中减去Er,完成回波采集过程中回波串数据的校正.之所以采用这一数据校正流程,而不直接用原始回波串数据乘以校正因子,是为了防止在校正过程中噪声信号随回波串信号放大的同时被放大.
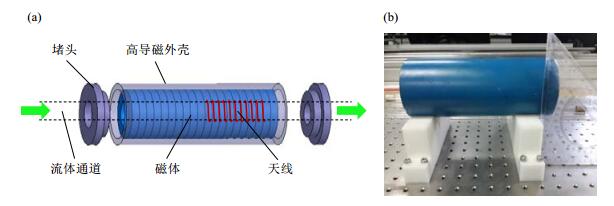
2 仪器及样品仪器采用自主研发的便携式流体分析探头(如图 3所示),探头长20 cm、外径为8 cm.其中磁体采用8段式Halbach环形磁体结构,材料为钐钴,磁体内部形成一个长15 cm、外径1 cm的圆柱形均匀磁场区域,该区域内磁场强度为78 mT.天线采用螺线管结构,长10 cm,包裹流体管并固
|
| 图 3 便携式核磁共振流体分析仪探头. (a) 探头结构示意图;(b) 探头实物图 Fig. 3 The probe of portable NMR fluid analyzer. (a) Probe schematic, (b) Probe photo |
定在在磁体均匀区域尾部.需要注意的是,天线前部磁场用于对样品进行预磁化,该段磁体越长,样品磁化的时间就越长;天线的长度越长,流动导致的信号损失率就越小.电子线路采用新西兰Magritek公司的kea 2 MHz谱仪,发射功率为400 W,死时间为15 μs,最小回波间隔为60 μs.
用纯水作为实验样品,流动测量时通过一个小型流体泵控制其在设定流速下流动,并在流体流动的过程中连续采集NMR信号.
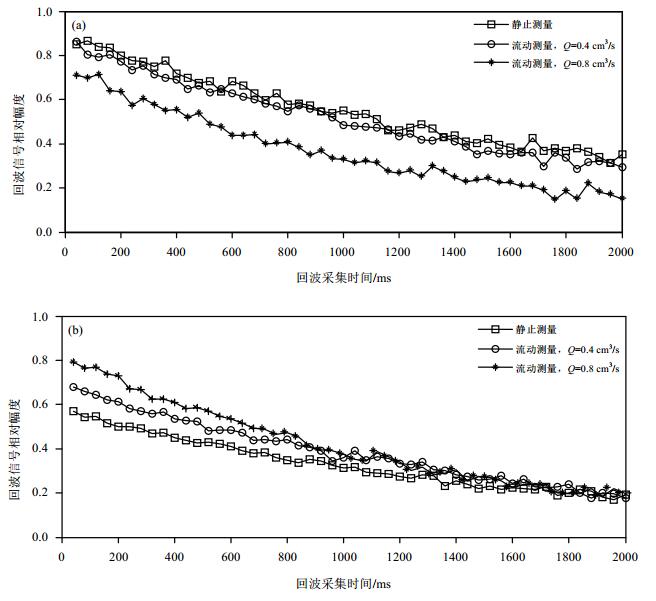
3 结果与讨论 3.1 未进行流动校正的NMR测量结果对纯水样品分别进行静止NMR测量和流动NMR测量,实验在室温环境(20 ℃左右)下进行,采用CPMG脉冲序列测量回波串数据,相关参数如下:TE=4 ms,N=500,只扫描一次且不进行信号叠加.一组实验中包含一次静止NMR测量实验,和两次流量分别为0.4 cm3/s、0.8 cm3/s的流动NMR测量实验.分别在TW=12 000 ms和TW=3 000 ms下进行两组实验,实验采集到的回波串数据如图 4所示.
|
| 图 4 纯水NMR静止测量和流动测量实验结果. (a) TW=12 000 ms, (b) TW=3 000 ms Fig. 4 Static and flow NMR measurement of pure water. (a) TW=12 000 ms, (b) TW=3 000 ms |
在图 4(a)中,TW=12 000 ms,TW > 4T1,即设定的TW可以保证样品完全磁化.当流体流量较小(0.4 cm3/s)时,流体流经探头LM长度的磁化区域的时间约为10 000 ms,基本可被完全磁化,所以回波串首幅值与静止测量时的接近;但是当流量增大到0.8 cm3/s时,流体磁化时间减小到5 000 ms左右,进入天线区域时不能完全磁化,所以回波串首幅值明显下降,即产生“磁化不充分”现象.
在图 4(b)中,TW=3 000 ms,不满足样品完全磁化的条件,静止条件下回波串的首幅值不到完全磁化时的2/3,但随着流量的增大和流速的增快,回波串首幅值变大,即产生“过度磁化”现象.
从两组实验中均可观察到,随着流量的增大,回波串衰减的速度变快,这就是由回波采集时间内产生的采集信号损失引起的.
3.2 经流动校正后的NMR测量结果图 5是对图 4两组回波串数据进行流动校正后的结果.校正后,回波串首幅值均得到了恢复,不同流量下的回波串衰减速度基本一致,但是仍然可以观察到,随着流量的增大,回波串衰减速度会略微变快.也就是说,除了流动速度所导致的回波衰减变快以外,仍然还有一些别的影响因素.初步分析是由于磁场分布沿流动方向不足够均匀,而流体在流动过程中并不是严格的保持“平移”运动,由此可能产生视扩散系数的变大,在不均匀场下会导致回波串衰减速度的进一步加快.由实验结果可知,对于内径为1 cm左右的圆管内流动流体,Q < 0.4 cm3/s时可通过校正控制流速对NMR测量的影响;但随着流量的进一步增加,校正结果误差变大,效果变差.

|
| 图 5 流动校正后的NMR流动测量结果. (a) TW=12 000 ms, (b) TW=3 000 ms Fig. 5 Flow NMR measurement with flowing correction. (a) TW=12 000 ms, (b) TW=3 000 ms |
流体在流动状态下,因所受压力和自身属性的不同呈现不同流态,一般流体在慢速流动下呈现结构流状态.流动状态本身会对NMR在线测量造成影响,体现在磁化时间不充分和回波采集信号损失两个方面:前者会影响回波串首幅值偏离正常值,后者会加速回波串信号的衰减.低流量(1 cm内径流体管、Q < 0.4 cm3/s时)下的流动影响可以进行量化分析,并通过回波串校正方法加以控制.但较大流量(1 cm内径流体管、Q≥0.4 cm3/s时)下,流动影响导致的信号损失量太大,且影响机理更为复杂时,该校正方法不再适用,可从探头优化设计[18, 19]和NMR多维在线测量脉冲序列[20-22]方面进行深入研究.
| [1] | COATS G R, XIAO L Z, PRAMMER M G, et al. NMR logging principles and applications[M]. Houston: Gulf Professional Publishing, 1999. |
| [2] | CASANOVA F, PERLO J, BLÜMICH B, et al. Single-sided NMR[M]. New York: Springer, 2011. |
| [3] | MATZKANIN G A, et al. A review of nondestructive of composites using NMR, in:nondestructive characterization of materials[M]. Berlin: Springer, 1989. |
| [4] | SURYAN J R. Nuclear resonance in flowing liquids[J]. Proc Indian Acad Sci Sect, 1951, 33: 107-111 |
| [5] | CAPRIHAN A, FUKUSHIMA E. Flow measurements by NMR[J]. Phys Rep, 1990, 198(4): 195-235 DOI:10.1016/0370-1573(90)90046-5 |
| [6] | SINGER J R. Blood flow rates by nuclear magnetic resonance measurements[J]. Science, 2013, 130(3389): 1652-1653 |
| [7] | AKKURT R. Effects of motion in pulsed NMR logging[D]. Colorado:Colorado School of Mines, 1990. |
| [8] | EDWARDS C M. Effect of tool design and logging speed on T2 NMR log data[C]. Houston:SPWLA's 38th Annual Logging Symposium, 1997. |
| [9] | MASAK P C, BOUTON J, PRAMMER M G, et al. Field test results and applications of the downhole magnetic resonance fluid analyzer[C]. Oiso:SPWLA 43rd Annual Logging Symposium, 2013. |
| [10] | LIU S H(刘双惠), XIAO L Z(肖立志), HU F L(湖法龙), et al. Studies on NMR logging responses at formation boundary(核磁共振测井地层界面响应特征研究)[J]. Chinese Journal of Geophysics(地球物理学报), 2008, 54(4): 1262-1269 |
| [11] | CHANH C M, JACK L, STEVEN C, et al. Methods and systems for applying speed correction to NMR echo data. U.S. 2012/0025820 A1[P]. 2012. |
| [12] | DENG F, XIAO L Z, LIU H B, et al. Effects and corrections for mobile NMR measurement[J]. Appl Magn Reson, 2013, 44(49): 1053-1065 |
| [13] | KOCHIN N E, KIBEL' I A, ROZE N V. Theoretical hydromechanics[J]. Phys Today, 2009, 19(3): 76 |
| [14] | BINGHAM E C, et al. Fluidity And plasticity[M]. USA: McGraw-Hill Book Co, 1922. |
| [15] | CASSON N, et al. A flow equation for pigment oil-suspen-sions of the printing ink type[M]. London: Pergamon Press, 1959. |
| [16] | HERSCHEL W H, BULKLEY R. Measurement of consistency as applied to rubber-benzene solutions:29th Annual Meeting of the American Society Testing Materials Atlantic City[C]. Proc ASTM, 1926, 26(Ⅱ):621-633. |
| [17] | BLOCH F. Nuclear induction[J]. Phys Rev, 1946, 70 |
| [18] | LI X(李新), WANG Z Z(王志战), LI S G(李三国), et al. Analysis and optimization of pre-polarization methodology for NMR logging(核磁共振测井的预极化分析与优化)[J]. Journal of China University of Petroleum(中国石油大学学报(自然科学版)), 2014, 38(5): 75-81 |
| [19] | ADOLPHI N L, MCDOWELL A F. NMR, instrumentation, and flow meter/controller continuously detecting MR signals, from continuously flowing sample material:US8710836[P]. 2014. |
| [20] | MITCHELL J, HÜRLIMANN M D, FORDHAM E J. A rapid measurement of T1/T2:the DECPMG sequence[J]. J Magn Reson, 2009, 200(2): 198-206 DOI:10.1016/j.jmr.2009.07.002 |
| [21] | SONG Y Q. Magnetic resonance at low magnetic field:multi-dimensional experiment of relaxation and diffusion[C]. Hang Zhou:Proceedings of the 18th national magnetic resonance conference, 2014. |
| [22] | DENG F, XIAO L Z, CHEN W L, et al. Rapid determination of fluid viscosity using low-field two-dimensional NMR[J]. J Magn Reson, 2014, 247: 1-8 DOI:10.1016/j.jmr.2014.08.003 |

本作品采用知识共享署名 4.0 国际许可协议进行许可。
 2017, Vol. 34
2017, Vol. 34



