文章信息
- 杜庆阳, 常严, 钱嵩松, 杨晓冬
- DU Qing-yang, CHANG Yan, QIAN Song-song, YANG Xiao-dong
- 针对磁共振射频脉冲的时频域分析方法比较研究
- Comparison of Time-Frequency Analysis Methods for Radio Frequency Pulses Used in Magnetic Resonance
- 波谱学杂志, 2016, 33(4): 646-654
- Chinese Journal of Magnetic Resonance, 2016, 33(4): 646-654
- http://dx.doi.org/10.11938/cjmr20160414
-
文章历史
收稿日期: 2016-04-11
收修改稿日期: 2016-10-24


DOI:10.11938/cjmr20160414
2. 中国科学院 苏州生物医学工程技术研究所, 江苏 苏州 215163
2. Suzhou Institute of Biomedical Engineering and Technology, Chinese Academy of Sciences, Suzhou 215163, China
射频脉冲在核磁共振(NMR)领域中扮演重要角色,借助射频脉冲可实现样本自旋体系的量子操控,从而产生预期的NMR信号,进而实现样本的波谱分析或成像应用.传统磁共振实验主要以矩形脉冲或sinc脉冲作为激发脉冲,但这些脉冲抵御射频场和主磁场非均匀性能力较差,因而局限于简单自旋体系.近年来,国内外研究者运用优化控制理论优化脉冲设计,可实现自旋体系的高保真状态迁移,从而获得理想的NMR信号.传统的时域分析或者频域分析仅能够反映射频脉冲幅度、相位随时间或者频率的单一变化情况.而通过优化控制方法得到的复杂形状脉冲的信号特征非常复杂,单一的时域或频域分析往往不能直观地反映出脉冲信号的幅度和相位信息随时间和频率变化的分布情况[1].而时频域分析法将一维信号放在二维的时频平面上进行分析,可以更加直观地表示磁共振射频脉冲的时频特征.这种方法包括短时傅里叶变换(STFT)、连续小波变换(CWT)、维格纳-威利分布(WVD)等,已被应用于声信号、地震数据和形状激光脉冲等多个领域的信号分析.通过对射频脉冲信号进行时频域分析,我们可以同时获取射频脉冲的时域信息和频域信息,从而为研究射频脉冲对复杂自旋体系的作用机制提供更加直观有效的分析手段[2].本文以分析用于量子伪纯态制备的优化脉冲特性为例,对上述几种时频分析方法在磁共振领域的应用进行了比较研究.
1 时频域分析方法 1.1 短时傅里叶变换(STFT)最早的时频域分析法是短时傅里叶变换,它于1946年被英国物理学家Gabor D提出.短时傅里叶变换的基本思想是假设信号在一个较短的时间内为平稳信号,通过一个短时窗函数对信号进行截取并对其进行傅里叶变换就可以得到这段时间内的信号频率分布.将窗函数沿时间方向移动,并分别计算出不同时间段的频率分布,即可得到信号随时间变化的频率分布情况.信号s(t)的短时傅里叶变换可以用下面公式表达:
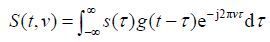
|
(1) |
其中,g(t)为窗函数.不同的窗函数具有不同的时频窗口面积,在时频窗口形状保持不变时,窗口面积越小则局部化描述能力越强,即时频分辨率越高;反之,则时频分辨率越低.常用的窗函数有高斯窗、矩形窗、汉宁窗、海明窗等,其中高斯窗具有最高的时频分辨率[3].
短时傅里叶变换相较于传统傅里叶变换将信号s(t)映射成一个时间和频率的二维函数,并且保持了傅里叶变换的基本性质,这是短时傅里叶变换所具有的优势.但短时傅里叶变换的不足在于,由于在整个时频域上用一个固定宽度的窗函数分析,并且其时频窗口面积不变,因此整个时频域内不能根据信号变化而自适应调整自身分辨率. 若要改变分辨率,则需重新选择窗函数[4, 5].
1.2 连续小波变换(CWT)小波变换法是由法国工程师Morlet J于1974年首先提出的,它可以通过伸缩和平移等运算功能将信号放在时间尺度平面进行多尺度特性分析,具有自适应性.连续小波变换的定义为:
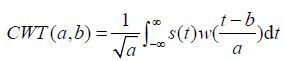
|
(2) |
其中,a为尺度因子,b为时移因子,大尺度对应信号的低频区,小尺度对应信号的高频区.函数w(t)为母小波,常用的小波有Harr小波、Morlet小波、Mexican hat小波、Gaussian小波和db小波等.尺度因子a和频率fab存在以下关系[6]:
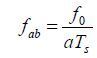
|
(3) |
其中f0为小波的中心频率,Ts为分析信号的采样周期.
小波变换的显著优势在于它可以根据信号的频率变化自动调节时域采样的疏密程度,在低频区对应信号的整体信息用大尺度分析,提高频率分辨率;在高频区信号波形变化较剧烈(即信号包含的细节信息较多)时用小尺度分析,提高时间分辨率,从而达到多分辨率分析信号时频域特性的目的.
1.3 维格纳-威利分布(WVD)维格纳-威利分布最初是由美国物理学家Wigner E P于1932年提出的,并首先用于量子力学研究,其后被Ville J A引入信号处理领域.维格纳-威利分布是一种非线性表示方法[4, 7],其表达式为:
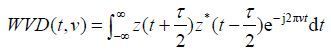
|
(4) |
其中,
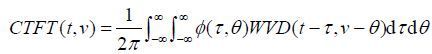
|
(5) |
(3) 式中的
维格纳-威利分布相较于线性变换具有很高的时间和频率分辨率,缺点是受到交叉项的影响导致在时频平面内出现伪影现象,即在时域或频域的两个峰值之间产生实际不存在的峰值.若
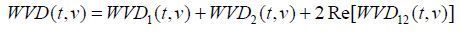
|
(6) |
(6) 式中,
量子计算通过利用量子力学中态的叠加、相干、纠缠特性,在解决某些问题时比经典计算更快、更有效[8].量子伪纯态作为量子计算中的初始态,其制备效率十分重要.然而随着量子位数的增加和信号指数性的衰减,量子位数越多制备伪纯态所需的脉冲序列越复杂,越不容易实现,不利于量子位数的扩展[9].作者所在研究组提出了一种基于优化控制的协作脉冲产生方法,并利用获得的协作脉冲实现了三自旋(丙氨酸分子体系)的特定量子态的状态转移[10].上述协作脉冲由多个相对独立的优化脉冲组成,本文将分别采用三种时频域分析方法对其中一个优化脉冲进行特性分析和比较.
自旋体系的动力学过程可利用量子力学理论的Liouville-von Neuman方程描述:
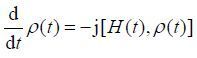
|
(7) |
其中
磁共振射频脉冲可表示为:
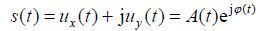
|
(8) |
其中s(t)是复脉冲信号,ux和uy分别为射频场的x和y分量.A(t)和分别代表时域的幅度和相位.其中
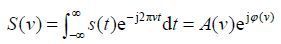
|
(9) |
这里S(v)为脉冲频谱,A(v)为频谱幅度和频谱相位,且
|
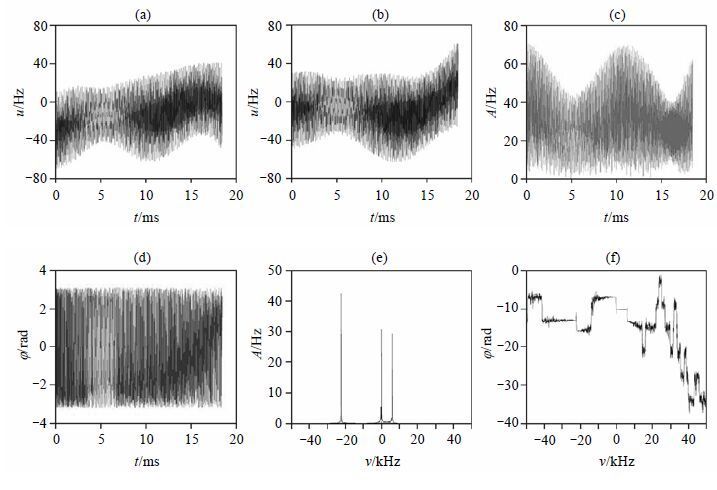
| 图 1 优化形状脉冲的时域及频域分析. (a) x分量;(b) y分量;(c) 时域幅度A(t);(d) 时域相位φ(t);(e) 频域幅度A(v);(f) 频域相位φ(v) Fig. 1 The temporal and spectral analysis of optimized pulse. (a) x components; (b) y components; (c) Temporal amplitude A(t); (d) Temporal phase φ(t); (e) Spectral amplitude A(v); (f) Spectral phase φ(v) |
可以看出,该脉冲幅度在整个频域内存在三个峰值,分别为-22 kHz、0 kHz和6 kHz,且与丙氨酸的化学位移一致.然而单一的时域或频域分析不能直观反映脉冲幅度、相位在时频域上的分布情况.
2.1 短时傅里叶分析根据1.1节的介绍,高斯窗进行短时傅里叶变换时具有最高的时频分辨率,因此我们选择高斯窗对优化脉冲进行分析.N点高斯窗的表达式为:
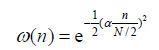
|
(10) |
其中
|
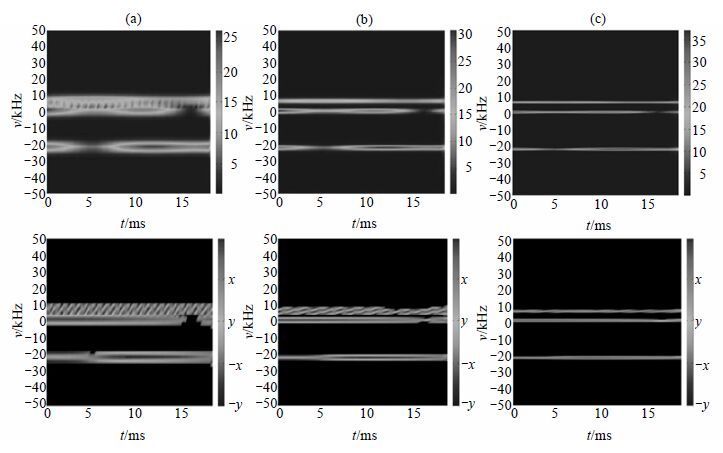
| 图 2 短时傅里叶分析结果. (a) N=100,α=3.0;(b) N=200,α=2.5;(c) N=400,α=2.0 Fig. 2 The results of STFT analysis. (a) N=100, α=3.0; (b) N =200, α=2.5; (c) N=400, α=2.0 |
文献[2]也采用短时傅里叶变换对几种常用的去偶序列的时频特性进行了分析,可以看出时频域分析法相较于单一的时域或频域分析更加直观地反映了脉冲幅度、相位在时频域上的分布情况,因此可以更好地揭示射频脉冲时频域特性与射频脉冲对自旋体系作用机制的内在关联.下文将对连续小波变换和维格纳-威利分布两种方法的优缺点进行比较研究.
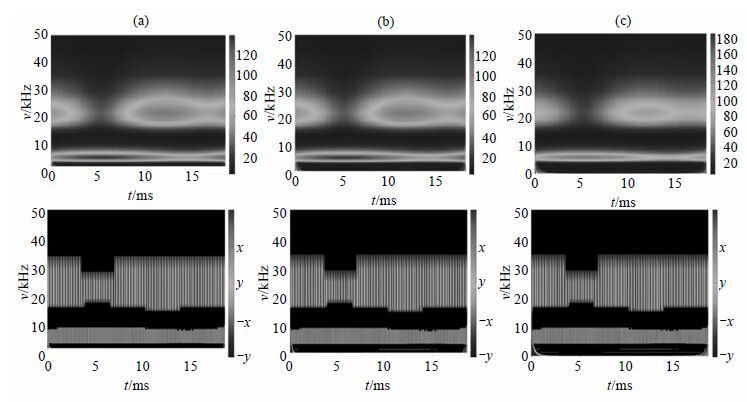
2.2 连续小波变换分析类似于短时傅里叶变换,图 3为采用Morlet小波的连续小波变换分析结果,其中第一行代表优化脉冲的时频域幅度分布,色标数值代表对应颜色处脉冲幅度大小;第二行代表优化脉冲的时频域相位分布,色标代表对应颜色处脉冲相位角在(x, y)平面上的方向.从左至右三列尺度范围逐渐增大,分别为1~64、1~128和1~512.根据1.2节的介绍,采用Morlet小波且优化脉冲的采样周期为4.55 ms时,尺度因子范围为1~64对应的频率范围为178.57~2.79 kHz,无法分析0 kHz处的脉冲时频域特性,因此图 3(a)列只在两个频率处出现幅度峰值;图 3(b)列的尺度范围为1~128,对应的频率范围为178.57~1.40 kHz,仍然无法分辨0 kHz时的幅度、相位分布情况;图 3(c)列的尺度范围为1~512,对应的频率范围为178.57~0.35 kHz,此时虽然可以观察到0 kHz附近出现峰值,但是其幅度、相位时频分布依然难以观察,尺度范围的增加也极大地增大了连续小波变换的计算量,因此连续小波变换不能较好地分析频率较低部分的优化脉冲时频域特性.此外,连续小波变换将优化脉冲映射到正半时频域,三个峰值的中心频率分别为22 kHz、6 kHz和0 kHz,无法分辨优化脉冲信号的正负频率.虽然连续小波变换具有上述缺点,但是相较于短时傅里叶变换也有其自身的优势.可以看出,连续小波变换具有多分辨率的特点,小尺度对应脉冲高频部分,具有较好的时间分辨率;大尺度对应低频部分,具有较高的频率分辨率.对射频脉冲而言,高频部分时域变化较为剧烈,因此需要较好的时间分辨率;低频部分时域变化较为平缓,而频率变化范围较小,因此需要较好的频率分辨率.连续小波变换的自适应性相较于短时傅里叶变换能够更好地反映射频脉冲在不同频率处的变化趋势.
|
| 图 3 连续小波变换分析结果. (a) 尺度范围1~64;(b) 尺度范围1~128;(c) 尺度范围1~512 Fig. 3 The results of CWT analysis. (a) Scale of 1~64; (b) Scale of 1~128; (c) Scale of 1~512 |
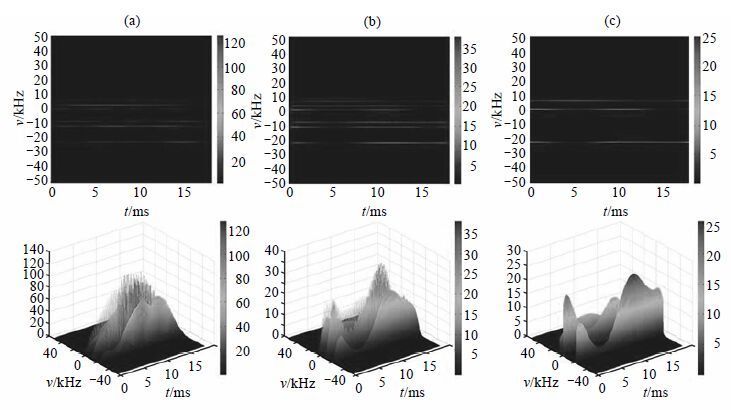
图 4为维格纳-威利分布分析结果,第一行为优化脉冲时频域幅度分布,第二行为优化脉冲的时频域幅度三维展示,色标数值表示对应颜色处脉冲幅度大小.可以观察到图 4(a)维格纳-威利分布分析结果受伪影影响较为严重.在两两幅度峰值中间存在伪影,分别位于3 kHz、-8 kHz和-11 kHz处;图 4(b)为伪维格纳-威利分布分析结果,此时伪影受到了一定的抑制,但是影响依然较为严重;图 4(c)列为平滑伪维格纳-威利分布(SPWVD)分析结果,对伪影具有较好的抑制,但是极大地增加了计算量.另外,维格纳-威利分布计算结果为实数,这在某些应用场合被作为一项优势,但在磁共振领域却是一个缺陷,因为它无法获得优化脉冲的相位时频域分布.尽管维格纳-威利分布具有上述缺点,但是其优势也较为明显,从图中可以看出维格纳-威利分布具有很高的时频分辨率,经过平滑处理后相较于短时傅里叶变换和连续小波变换更为精确地反映了射频脉冲在时频域的分布区域.
|
| 图 4 维格纳-威利分布(WVD)分析结果. (a) WVD分析结果;(b) 伪WVD(PWVD)分析结果;(c) 平滑伪WVD(SPWVD)分析结果 Fig. 4 The result of WVD analysis. (a) The result of WVD; (b) The result of PWVD; (c) The result of SPWVD |
本文从分析磁共振射频优化脉冲的时频域特性入手,对短时傅里叶变换、连续小波变换、维格纳-威利分布等分析方法的优缺点进行了比较研究.短时傅里叶变换需要选择合适的窗函数及窗口大小,可以直观反映射频脉冲幅度、相位的时频域总体分布;连续小波变换具有较好的自适应性,能够更好地反映射频脉冲幅度、相位在不同频率处的变化趋势,对于频率不是很低的射频脉冲分析较为适合;维格纳-威利分布具有很高的时频分辨率,经过平滑处理后能够精确地反映射频脉冲的时频域分布区域.实际分析中,根据需要可以结合各自的优势对射频脉冲进行多种方法分析,以便更好地理解复杂脉冲的幅度、相位特性在时频域的分布情况.
| [1] | Yan Tian-feng(严天峰), Yan Ting-li(颜挺利) . Radio spectrum multi-domains analysis based on STFT(基于STFT的无线电频谱信号的多域分析)[J]. Information Technology(信息技术) , 2010 (11) : 163-165 |
| [2] | Köcher S S, Heydenreich T, Glaser S J . Visualization and analysis of modulated pulses in magnetic resonance by joint time-frequency representations[J]. J Magn Reson , 2014, 249 : 63-71 DOI:10.1016/j.jmr.2014.10.004 |
| [3] | Liu Lin(刘林), Hao Bao-guo(郝保国) . Theory and application of time-frequency analysis(时频分析理论和应用)[J]. Computer Automated Measurement & Control(计算机测量与控制) , 2001, 9 (4) : 44-45 |
| [4] | Dong Jian-hua(董建华), Gu Han-ming(顾汉明), Zhang Xing(张星) . A comparison of time-frequency analysis methods and their applications(几种时频分析方法的比较及应用)[J]. Chinese Journal of Engineering Geophysics(工程地球物理学报) , 2007, 4 (4) : 312-316 |
| [5] | Veer K, Agarwal R . Wavelet and short-time Fourier transform comparison-based analysis of myoelectric signals[J]. J Appl Stat , 2015, 42 (7) : 1591-1601 DOI:10.1080/02664763.2014.1001728 |
| [6] | Li Nan(李楠), Zhou Bo(周波) . Relations among the different frequencies and wavelet scale in signal processing(信号处理中各种频率以及小波尺度的关系)[J]. Journal of EEE(电气电子教学学报) , 2008, 30 (6) : 15-17 |
| [7] | Huang H B, Li R X, Huang X R et al . Sound quality evaluation of vehicle suspension shock absorber rattling noise based on the Wigner-Ville distribution[J]. Appl Acoust , 2015, 100 : 18-25 DOI:10.1016/j.apacoust.2015.06.018 |
| [8] | Zhang Ya-juan(张亚娟), XuanYa-nan (轩亚楠), Wei Da-xiu(魏达秀) . NMR experimental implementation of cluster state(Cluster态的核磁共振实验制备)[J]. Chinese J Magn Reson(波谱学杂志) , 2014, 31 (1) : 108-115 |
| [9] | Tian Jia-xin(田佳欣), Liu Wen-qing(刘文卿), Song Yan-hong(宋艳红) et al . Implementation of Deutsch algorithm using para-hydrogeninduced polarization(利用仲氢诱导极化技术实现Deutsch算法)[J]. Chinese J Magn Reson(波谱学杂志) , 2015, 32 (4) : 618-627 |
| [10] | Wei D, Chang Y, Glaser S J et al . Cooperative pulses for pseudo-pure state preparation[J]. Appl Phys Lett , 2014, 104 (2) : 242409 |

本作品采用知识共享署名 4.0 国际许可协议进行许可。
 2016, Vol. 33
2016, Vol. 33



