文章信息
- 赵欣欣, 薄斌仕, 刘田, 王乙, 李建奇
- ZHAO Xin-xin, BO Bin-shi, LIU Tian, WANG Yi, LI Jian-qi
- 定量磁化率成像多回波相位拟合算法研究
- A Phase Fitting Algorithm for Multi-Echo Quantitative Susceptibility Mapping
- 波谱学杂志, 2016, 33(4): 609-617
- Chinese Journal of Magnetic Resonance, 2016, 33(4): 609-617
- http://dx.doi.org/10.11938/cjmr20160410
-
文章历史
收稿日期: 2016-04-04
收修改稿日期: 2016-10-24


DOI:10.11938/cjmr20160410
2. Department of Radiology, Weill Medical College, Cornell University, Ithaca, New York 10021, USA;
3. Department of Biomedical Engineering, Cornell University, Ithaca, New York 14853, USA
2. Department of Radiology, Weill Medical College, Cornell University, Ithaca, New York 10021, USA;
3. Department of Biomedical Engineering, Cornell University, Ithaca, New York 14853, USA
定量磁化率成像(quantitative susceptibility mapping, QSM)利用一般磁共振成像(magnetic resonance imaging, MRI)技术舍弃的相位信息得到局部磁场变化特性,再通过复杂的场到源反演计算,可直接得到定量磁化率分布图[1-9]. 单回波或多回波梯度回波(gradientecho, GRE)序列可用来获取QSM反演计算需要的磁场分布图. 与单回波GRE序列相比,多回波序列一次激发可采集多个回波,这有利于相位解缠绕;且对磁化率更加敏感,得到的磁化率分布图信噪比也更高[10-12]. 有研究表明采用5~10个回波可获得较好的颅内核团磁化率对比[13].
QSM重建时,多回波相位数据首先需进行时间域相位解缠绕,然后通过线性拟合得到磁场分布图,再进行后续处理. 常用的线性拟合算法是加权最小二乘法(weighted linear least-square,WLS),其原理是按照一定规则设置权重系数,以调整各回波在拟合中的权重,使拟合出的相位逐步逼近真实值. 权重系数的设置可根据梯度回波信号随回波时间的衰减特性,从模图提取信息,将回波时间较短、信号较强的回波赋予较大权重;反之,则赋予较小权重[5, 14]. 这种权重系数结合了模图中的组织结构信息,一定程度上突出了组织间的对比.
采用上述常规WLS算法得到的磁化率分布图具有以下特征:对于白质和基底节等磁化率均匀的区域,组织显示清晰;但是对于颅底部位,由于颅脑空腔处组织-空气界面的磁化率极不均匀,这会引起较大的局部磁场变化,导致组织信号强度衰减很快,使得磁化率分布图上相应组织的信噪比较低,有些结构甚至模糊不清. 而靠近颅底部位的黑质磁化率是定量评价某些神经退行性疾病(如帕金森病)的重要生物指标[15-18],因此提高颅底部位磁化率分布图的图像质量非常重要.
在WLS数据拟合方法中,为了减少低信噪比的数据点对拟合结果的影响,可对常规WLS算法进行适当的修改. 例如,在图像内插处理时,先采用双边滤波将信噪比低的信号以及噪声数据点剔除,再采用常规WLS算法进行拟合[19];在进行横向弛豫率(R2*)多回波拟合时,在常规WLS算法的基础上进行阈值截断,可明显改善R2*的图像质量[20].
针对常规WLS算法在多回波相位拟合中的不足,本文提出了截断WLS算法:在采用常规WLS算法拟合之前引入阈值截断条件,剔除信噪比较低的回波信号,以期提高磁化率分布图像质量. 本文通过颅脑QSM实验验证了该方法的可行性与有效性.
1 截断WLS算法对于多回波GRE序列,空间某个像素第i个回波的相位可表示为:
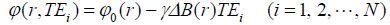
|
(1) |
其中表示初相位,表示旋磁比,r表示像素的空间位移,N表示最大回波数,表示局部磁场变化. 等间隔回波时间(
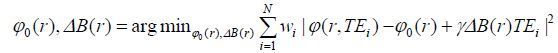
|
(2) |
其中
在拟合过程中,权重系数的选取非常关键. 可根据磁共振信号随时间的衰减规律,从模图提取信息,如某体素第i个回波的权重系数
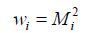
|
(3) |
其中
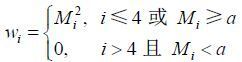
|
(4) |
其中a为既定阈值. 基于本文的实验参数设置,几乎所有体素的信号幅度值在第4个回波(TE= 27.2 ms)仍能保持较高的信噪比,之后不同区域的体素信号随时间的衰减情况出现了分化:有的体素(如白质区域)的信号幅值仍然随时间呈指数性衰减,但有的体素(如颅底区域)的信号幅值由于受噪声影响较大而迅速衰减. 因此,为保证一定的信噪比,从第5个回波开始判断是否需要截断.
选取的阈值要满足以下要求:既要将信号低的回波截断,使其不再参与相位拟合;又要保证尽可能多的回波参与拟合,以提高磁化率分布图的信噪比[21]. 本文取模图噪声的30倍作为截断阈值的经验值,而模图噪声按照如下方法计算:取第1回波模图 4个角一定大小的感兴趣区域(region of interest,ROI)中体素的幅值标准差作为噪声[22]. 确定好阈值之后,每个体素的多回波数据均根据(4) 式进行选择性截断. 由于不同体素的信号强度不同,因此其截断的回波数目也不同,这样可尽量保证不同组织均具有相对较高的信噪比.
2 材料与方法 2.1 数据采集5名(3名女性、2名男性)年龄为(25.8±1.3)岁的健康被试参与该项研究,实验前要求被试认真阅读并签署MRI检查知情同意书.
所有被试扫描均在3 T MRI设备(西门子MAGNETOM Trio Tim 3 T)上完成,采用12通道头线圈作为信号接收线圈. 扫描序列为三维多回波GRE序列,具体参数如下:重复时间(TR)= 60 ms,第一回波时间(TE1)= 6.8 ms,回波间隔(ΔTE)= 6.8 ms,回波数(N)= 8,翻转角(FA)= 15˚,视野(FOV)= 240×180 mm2,像素= 0.625 mm× 0.625 mm×2 mm,层数(slices)= 96. 为减少采样时间,在相位编码方向(被试左右方向)采用并行采样技术,加速因子为2. 为评价改进算法的降噪效果,所有被试连续两次进行三维多回波GRE序列扫描,扫描时间共15.5 min.
2.2 QSM重建采用基于形态学的偶极子反演(morphology enabled dipole inversion,MEDI)方法重建出颅脑横断位磁化率分布图[6, 23],该重建方法通过l1范数进行正则化,并对拉格朗日乘子(λ)、迭代次数以及噪声水平等参数进行了优化. 具体重建步骤如下:首先由不同回波的原始模图求均方根得到组合模图,再由组合模图获取形态学梯度加权图;由多回波原始相位图拟合出磁场分布图;将拟合出的磁场分布图依次采用区域增长算法进行空间解缠绕[24]、偶极场投影(projection onto dipole fields,PDF)方法去除背景场[5],最终结合梯度加权图反演重建出定量磁化率分布图. 进行多回波相位拟合时分别采用常规WLS算法以及截断WLS算法对加权系数进行调整.
2.3 数据分析在磁化率分布图上利用MRICro软件(www.micro.com)在核团显示最清晰的层面上分别勾画出红核、黑质、尾状核头、苍白球、壳核的左、右ROI(图 1). 为检验改进算法的有效性,对两种拟合算法得到的磁化率分布图的噪声水平进行对比评价. 将连续两次扫描得到的分布图相减得到磁化率分布差图[25],将勾画出的核团ROI加载到分布差图上,计算出磁化率分布图中各核团的噪声. 每个ROI的磁化率分布图噪声定义为ROI内所有体素在磁化率分布差图上的标准差[26].
采用非参数统计的配对样本Wilcoxon方法检验两种算法的噪声水平的差异性,所用软件为SPSS 17.0(p< 0.05表示差异显著).

|
| 图 1 颅底及基底节核团ROI示意图. RN:红核;SN:黑质,CN:尾状核头;GP:苍白球;PU:壳核;R:右侧;L:左侧 Fig. 1 ROIs on the QSM map. The ROIs were drawn manually for right (R) and left (L) red nucleus (RN), substantia nigra (SN), caudate nucleus (CN), globus pallidus (GP) and putamen (PU) |
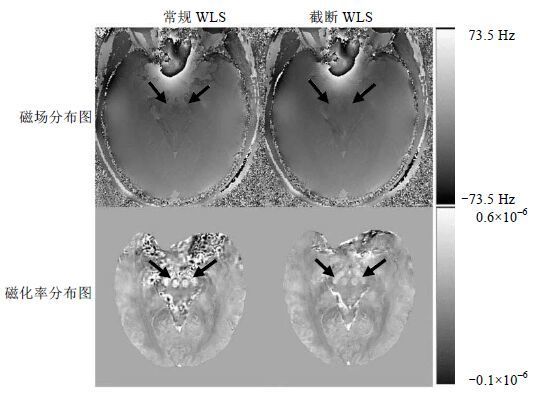
图 2为一例健康志愿者颅底部位采用常规WLS和截断WLS两种算法拟合得到的磁场分布图(左上图和右上图)和对应的磁化率分布图(左下图和右下图). 可以发现,采用常规WLS算法拟合出的颅底部位磁场分布图具有非常明显的伪影(左上图),对应的磁化率分布图中颅底结构非常模糊(左下图). 与之相比,采用截断WLS算法拟合出的磁场分布图更加平滑(右上图),对应的磁化率分布图上组织对比更加清晰(右下图).
|
| 图 2 一健康志愿者颅底部位(箭头所指)采用常规WLS与截断WLS两种算法得到的磁场分布图与对应的磁化率分布图 Fig. 2 Field maps and quantitative susceptibility maps in the bottom of brain (arrow) from a young healthy subject reconstructed with conventional WLS and truncated WLS method |
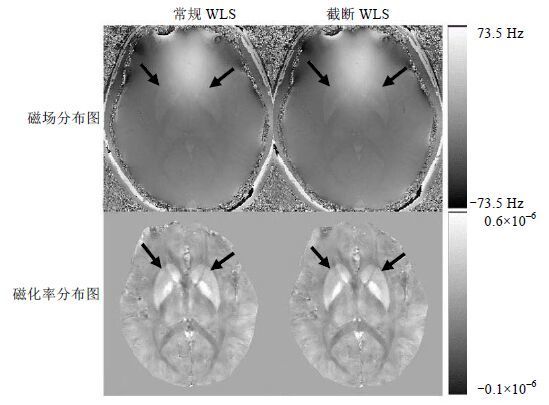
图 3是基底节部位采用两种算法拟合得到的磁场分布图(左上图和右上图)和对应的磁化率分布图(左下图和右下图),结果显示两种方法得到磁场分布图和磁化率分布图未显示明显差别,磁场分布图均未见明显伪影,磁化率分布图中深部核团与周围白质对比均很明显.
|
| 图 3 一健康志愿者基底节部位(箭头所指)采用常规WLS与截断WLS两种算法拟合得到的磁场分布图与对应的磁化率分布图 Fig. 3 Field maps and quantitative susceptibility maps in the basal ganglia (arrow) from a young healthy subject reconstructed with conventional WLS and truncated WLS method |
5名被试各个灰质核团采用两种拟合算法得到的磁化率分布图噪声的平均值与标准差如表 1所示,其柱状图如图 4所示. 结果显示:对于颅底部位(红核和黑质),采用截断WLS算法可使磁化率分布图上双侧红核和黑质部位噪声显著下降(p < 0.05),截断WLS算法得到的平均噪声约为常规WLS算法的1/3~1/2;对于基底节部位(尾状核、苍白球和壳核),截断WLS算法导致磁化率分布图上深部核团(尾状核、苍白球、壳核)的噪声略有上升,但没有显著差别.
| 核团 | 常规WLS | 截断WLS | p值 | |
| 红核 | 左侧 | 0.042±0.020 | 0.019±0.009 | 0.043* |
| 右侧 | 0.042±0.019 | 0.020±0.006 | 0.043* | |
| 黑质 | 左侧 | 0.069±0.048 | 0.030±0.019 | 0.043* |
| 右侧 | 0.098±0.051 | 0.027±0.013 | 0.043* | |
| 尾状核 | 左侧 | 0.015±0.007 | 0.018±0.007 | 0.225 |
| 右侧 | 0.015±0.004 | 0.015±0.005 | 0.492 | |
| 苍白球 | 左侧 | 0.021±0.005 | 0.025±0.006 | 0.078 |
| 右侧 | 0.020±0.004 | 0.024±0.005 | 0.066 | |
| 壳核 | 左侧 | 0.014±0.006 | 0.018±0.009 | 0.104 |
| 右侧 | 0.014±0.006 | 0.016±0.006 | 0.066 | |
| * p < 0.05,具有显著差异 | ||||

|
| 图 4 分别采用常规WLS与截断WLS算法得到的灰质核团磁化率分布图噪声水平对比. RN:红核;SN:黑质;CN:尾状核头;GP:苍白球;PU:壳核,L左侧;R右侧;* p < 0.05,具有显著差异 Fig. 4 Bar chart showing susceptibility noise in the deep gray matter nuclei with conventional WLS and truncated WLS methods for right (R) and left (L) red nucleus (RN), substantia nigra (SN), caudate nucleus (CN), globus pallidus (GP) and putamen (PU). * p < 0.05 shows significant difference |
针对QSM重建中常规WLS算法拟合局部变化较大的磁场的不足,本文构建了一种截断WLS算法. 对两种拟合算法得到的磁化率分布图噪声水平对比研究发现,截断WLS算法可有效提高颅底部位磁化率分布图的图像质量. 常规WLS算法得到的磁化率分布图上,红核、黑质等颅底部位核团的噪声非常大,而截断WLS算法得到的颅底核团磁化率分布图的噪声明显下降(表 1、图 2、图 4). 但是值得注意的是,对于基底节部位,截断WLS算法导致磁化率分布图噪声略有上升,但无显著差异,造成该现象的原因可能是在采用截断WLS算法进行选择性截断时,将低于阈值但衰减性较好的信号剔除,即过度截断了回波信号,导致基底节部位磁化率分布图信噪比略有下降.
理论上讲,水中质子的磁共振信号应随时间呈指数型衰减[1]. 但是组织间的磁化率差异使其信号也受到了不同程度的影响. 年轻被试大脑的基底节核团磁化率分布比较均匀,信号幅值随回波时间呈指数性衰减;但是对于颅底部位,如红核、黑质等核团,由于颅底空腔处组织-空气界面的磁化率差异较大,并且颅底处大脑静脉中的脱氧血红蛋白具有较强的顺磁性,与周围其他组织的磁化率差异也较大[4],而GRE序列对磁化率差异非常敏感[27],导致该 处组织的磁共振信号迅速衰减,直接影响最终磁化率分布图的信噪比. 因此,在多回波相位拟合时,对不同的组织必须采用合适的回波数目,既要保证组织间的对比度,又要去除个别部位信噪比较差的信号,尽量在信号大幅度衰减前获取有用信息[28].
常规WLS算法对于所有组织都采用相同的回波数(本文中均采用8个回波),无法兼顾不同信噪比磁化率分布图的组织. 大脑的某些组织,尤其颅底部位,其磁化率分布很不均匀,局部磁场变化较大,造成相位迅速离散,若回波时间较长,信号甚至可能衰减至噪声水平[29]. 因此对于这些核团,采用所有回波反而将噪声信号也一并拟合到局部磁场中,导致拟合出的场图在颅底部位的误差较大,最终反演出的磁化率分布图在该部位信噪比较低. 截断WLS算法有效避免了这一弊端,其根据不同组织的信号衰减程度,合理选择回波数目,剔除信噪比低的回波,一定程度上提高了颅底部位磁化率分布图的信噪比.
本研究提出的截断WLS算法还有以下几点不足:第一,给定的截断阈值为第一回波模图的噪声标准差的30倍,该数字是一经验值,今后应该寻求一种更为客观的阈值计算方法,对不同情况(如不同的回波数目、回波时间)下的数据进行合理的选择性截断;第二,进行选择性截断时,可能会将低于既定阈值但衰减性较好的信号剔除,导致某些区域组织的信噪比略有降低.
4 结论采用常规WLS算法对多回波相位拟合得到的局部磁场误差较大,导致颅底部位的磁化率分布图信噪比较低. 本文对常规WLS算法进行改进,在拟合之前加入信号截断条件,根据信号幅值的衰减程度进行选择性截断,剔除信噪比较低的信号,有效改善了颅底部位磁化率分布图的图像质量. 截断WLS算法为提高颅底磁化率分布图质量提供了一种新思路,可提高某些神经退行性疾病如帕金森病铁沉积定量评价的可靠性.
| [1] | Wang Y, Liu T . Quantitative susceptibility mapping (QSM):Decoding MRI data for a tissue magnetic biomarker[J]. Magn Reson Med , 2015, 73 (1) : 82-101 DOI:10.1002/mrm.25358 |
| [2] | Li W, Wu B, Liu C . Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition[J]. Neuroimage , 2011, 55 (4) : 1645-1656 DOI:10.1016/j.neuroimage.2010.11.088 |
| [3] | Haacke E M, Liu S, Buch S et al . Quantitative susceptibility mapping:current status and future directions[J]. Magn Reson Imaging , 2015, 33 (1) : 1-25 DOI:10.1016/j.mri.2014.09.004 |
| [4] | Liu C, Li W, Tong K A et al . Susceptibility-weighted imaging and quantitative susceptibility mapping in the brain[J]. J Magn Reson Imaging , 2015, 42 (1) : 23-41 DOI:10.1002/jmri.24768 |
| [5] | Liu T, Khalidov I, de Rochefort L et al . A novel background field removal method for MRI using projection onto dipole fields (PDF)[J]. NMR Biomed , 2011, 24 (9) : 1129-1136 DOI:10.1002/nbm.v24.9 |
| [6] | Liu J, Liu T, de Rochefort L et al . Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map[J]. Neuroimage , 2012, 59 (3) : 2560-2568 DOI:10.1016/j.neuroimage.2011.08.082 |
| [7] | de Rochefort L, Liu T, Kressler B et al . Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization:validation and application to brain imaging[J]. Magn Reson Med , 2010, 63 (1) : 194-206 |
| [8] | Shmueli K, de Zwart J A, van Gelderen P et al . Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data[J]. Magn Reson Med , 2009, 62 (6) : 1510-1522 DOI:10.1002/mrm.v62:6 |
| [9] | Wang A-li(王阿莉), Lin Jian-zhong(林建忠), Liu Wei-jun(刘伟俊) et al . Quantitative susceptibility mapping(定量磁化率成像重建方法及其应用)[J]. Chinese J Magn Reson(波谱学杂志) , 2014, 31 (1) : 133-154 |
| [10] | Fritzsch D, Reiss-Zimmermann M, Trampel R et al . Seven-tesla magnetic resonance imaging in Wilson disease using quantitative susceptibility mapping for measurement of copper accumulation[J]. Invest Radiol , 2014, 49 (5) : 299-306 DOI:10.1097/RLI.0000000000000010 |
| [11] | Li J Q, Chang S X, Liu T et al . Phase-corrected bipolar gradients in multi-echo gradient-echo sequences for quantitative susceptibility mapping[J]. Magn Reson Mater Phy , 2015, 28 (4) : 347-355 DOI:10.1007/s10334-014-0470-3 |
| [12] | Gilbert G, Savard G, Bard C et al . Quantitative comparison between a multiecho sequence and a single-echo sequence for susceptibility-weighted phase imaging[J]. Magn Reson Imaging , 2012, 30 (5) : 722-730 DOI:10.1016/j.mri.2012.02.008 |
| [13] | Wang Y . Quantitative Susceptibility Mapping:Magnetic Resonance Imaging of Tissue Magnetism[M]. Seattle: Createspace, 2013 : p228 . |
| [14] | Kressler B, de Rochefort L, Liu T et al . Nonlinear regularization for per voxel estimation of magnetic susceptibility distributions from MRI field maps[J]. IEEE Trans Med Imaging , 2010, 29 (2) : 273-281 DOI:10.1109/TMI.2009.2023787 |
| [15] | Murakami Y, Kakeda S, Watanabe K et al . Usefulness of quantitative susceptibility mapping for the diagnosis of Parkinson disease[J]. Am J Neuroradiol , 2015, 36 (6) : 1102-1108 DOI:10.3174/ajnr.A4260 |
| [16] | Barbosa J H, Santos A C, Tumas V et al . Quantifying brain iron deposition in patients with Parkinson's disease using quantitative susceptibility mapping, R2 and R2*[J]. Magn Reson Imaging , 2015, 33 (5) : 559-565 DOI:10.1016/j.mri.2015.02.021 |
| [17] | Du G, Liu T, Lewis M M et al . Quantitative susceptibility mapping of the midbrain in Parkinson's disease[J]. Mov Disord , 2016, 31 (3) : 317-324 DOI:10.1002/mds.26417 |
| [18] | He N, Ling H, Ding B et al . Region-specific disturbed iron distribution in early idiopathic Parkinson's disease measured by quantitative susceptibility mapping[J]. Hum Brain Mapp , 2015, 36 (11) : 4407-4420 DOI:10.1002/hbm.22928 |
| [19] | Hung K W, Siu W C. Improved image interpolation using bilateral filter for weighted least square estimation[C]. Hong Kong:Proceedings to IEEE International Conference on Image Processing, 2010:3297-3330. |
| [20] | Yin X, Shah S, Katsaggelos A K et al . Improved R2* measurement accuracy with absolute SNR truncation and optimal coil combination[J]. NMR Biomed , 2010, 23 (10) : 1127-1136 DOI:10.1002/nbm.v23.10 |
| [21] | Lotfipour A K, Wharton S, Schwarz S T et al . High resolution magnetic susceptibility mapping of the substantia nigra in Parkinson's disease[J]. J Magn Reson Imaging , 2012, 35 (1) : 48-55 DOI:10.1002/jmri.v35.1 |
| [22] | Lv Z, Jiang H, Xu H et al . Increased iron levels correlate with the selective nigral dopaminergic neuron degeneration in Parkinson's disease[J]. J Neural Transm , 2011, 118 (3) : 361-369 DOI:10.1007/s00702-010-0434-3 |
| [23] | Liu T, Wisnieff C, Lou M et al . Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping[J]. Magn Reson Med , 2013, 69 (2) : 467-476 DOI:10.1002/mrm.24272 |
| [24] | Ma J F, Son J B, Hazle J D . An improved region growing algorithm for phase correction in MRI[J]. Magn Reson Med , 2015 DOI:10.1002/mrm.25892 |
| [25] | Association N E M . Determination of Signal-to-Noise Ratio (SNR) in Diagnostic Magnetic Resonance Imaging[M]. Rosslyn: National Electrical Manufacturers Association, 2008 . |
| [26] | Haacke E M, Tang J, Neelavalli J et al . Susceptibility mapping as a means to visualize veins and quantify oxygen saturation[J]. J Magn Reson Imaging , 2010, 32 (3) : 663-676 DOI:10.1002/jmri.v32:3 |
| [27] | Dong Fang(董芳), Pei Meng-chao(裴孟超), Wang Qian-feng(王前锋) et al . Gradient echo imaging of the human brain:Respiratory induved artifacts and navigator echo correction(颅脑梯度回波成像:呼吸伪影和导航回波矫正)[J]. Chinese J Magn Reson(波谱学杂志) , 2014, 31 (3) : 321-330 |
| [28] | Groger A, Berg D . Does structural neuroimaging reveal a disturbance of iron metabolism in Parkinson's disease? Implications from MRI and TCS studies[J]. J Neural Transm , 2012, 119 (12) : 1523-1528 DOI:10.1007/s00702-012-0873-0 |
| [29] | Chan W C, Tejani Z, Budhani F et al . R2* as a surrogate measure of ferriscan iron quantification in thalassemia[J]. J Magn Reson Imaging , 2014, 39 (4) : 1007-1011 DOI:10.1002/jmri.24216 |

本作品采用知识共享署名 4.0 国际许可协议进行许可。
 2016, Vol. 33
2016, Vol. 33



