引言

传统的磁共振成像（magnetic resonance imaging，MRI）作为一种无辐射、非侵入的成像手段，可以提供信息含量丰富的软组织对比度图像^[1-3]，已成为临床医学中一种常规的影像诊断技术.然而，对于超快速弛豫组织如软骨、骨骼、肺、钙化病灶等，因其横向弛豫时间（T₂）极短，传统MRI方法却无能为力^[4-6].这是由于传统MRI脉冲序列的回波时间（echo-time，TE）远大于超快速弛豫组织的T₂，在信号采样时，快速弛豫组织的核磁共振（nuclear magnetic resonance，NMR）信号已衰减至难以检测.

对于超快速弛豫组织的成像，需要采用有别于常规MRI方法的超短回波时间脉冲序列.目前，比较流行的超短回波时间脉冲序列包括单点成像（single point imaging，SPI）、ZTE（zero echo-time imaging）、SWIFT（sweep imaging with Fourier transformation）和超短回波时间（ultra-short echo-time，UTE）成像等等.其中，SPI在一次扫描中仅采集三维k空间中的一个点，需要漫长的扫描时间，即使利用其加速形式——SPRITE（single-point ramped imaging with T₁ enhancement），扫描时间在临床应用中依然不可容忍.ZTE是一种三维射线采样序列，其在编码梯度稳定后施加射频脉冲并立即进行采样，由于ZTE采用短而强的射频脉冲，使其比吸收率（specific absorption rate，SAR）很高，不利于临床应用.SWIFT引入绝热脉冲进行激发，可以降低比吸收率，但需要在脉冲激发期间采样，对射频线圈和接收系统的要求很高.相比于以上脉冲序列，UTE是一种潜在的可能应用于临床的超短回波时间脉冲序列，其具有成像速度较快、成像比吸收率值较低、对硬件系统要求较低等优点.

但是，与成熟的常规MRI方法相比，目前UTE成像方法的实际应用还存在一定的困难.原因在于UTE序列从梯度边沿开始沿射线轨迹采集自由感应衰减（free induction decay, FID）信号填充k空间，对梯度涡流和梯度延时等因素引起的k空间轨迹失真极度敏感，若不在采样或者重建时进行校正，将产生严重的图像伪影，包括模糊、阴影和几何变形等.采样时的校正是指在脉冲序列中调整采样门控信号的位置，使其时序能够与梯度精确对准，这种方法能在很大程度上降低k空间轨迹失真的影响，但不能校正涡流的影响；且当梯度通道之间存在延时不均衡时，也难以完全消除梯度延时的影响.重建时的校正是指用真实k空间轨迹而非理想k空间轨迹进行图像重建，较常用的方法是先测量k空间轨迹^[12]，再以此重建图像.这种方法一般可以取得很好的效果，但非常耗时.另一种方法是测量梯度系统的频率响应函数^[13]，再据此估计真实k空间轨迹，这种方法可以显著提高k空间轨迹校正的时效性，但梯度系统的频率响应函数测量过程十分复杂.考虑到大多数情形下，梯度涡流和梯度延时是引起轨迹失真的主要因素，Atkinson等人^[14]提出了一种简便的真实k空间轨迹估计方法：在空间中多个位置，测量多个梯度下的一组k空间轨迹曲线，并建立在梯度涡流和梯度延时影响下的k空间轨迹曲线数学模型，通过最小化理论k空间曲线与测量值的误差，求取系统的梯度涡流常数和梯度延时，再用这些参数来校正k空间轨迹.这种方法便于实现且时效性高.但实际应用时，梯度延时与时间常数很小的涡流表现极其相似^{[15, 19]}，二者很难区分，这种方法缺少对涡流常数取值的限制，难以保证总是获得最优的一组解.

针对以上问题，本文在Atkinson等人提出的轨迹估计方法的基础上，针对以梯度涡流和梯度延时为主要因素引起的k空间轨迹失真，提出了一种改进的UTE序列轨迹校正方法：首先测量MRI系统的残余涡流曲线和UTE序列k空间轨迹，将最小化k空间轨迹误差和涡流曲线误差作为两个目标函数；然后求解这一约束多目标优化问题，避免涡流和延时影响的混淆，最终确定梯度延时和涡流常数；再以这组系统参数校正k空间的轨迹.

1 理论与方法 1.1 k空间轨迹失真的来源 1.1.1 梯度涡流

由电磁感应定律可知，在梯度切换时，磁体空间内的导体结构中将产生感应电流，导致实际梯度场与理想梯度场产生偏差.MRI中通常称这些感应电流为梯度涡流^{[17, 18]}.一般来说，MRI梯度涡流的阶跃电流响应可写为如下的多指数衰减形式：

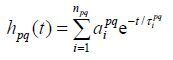
(1)

其中t代表时间；p代表梯度场的空间分布形式，包括X、Y、Z三种；q代表涡流的空间分布形式，如B₀、X、Y、Z等；${{n}_{pq}}$、$a_{i}^{pq}$与$\tau _{i}^{pq}$分别代表梯度场p引起的q空间分布涡流的项数、第i项幅度常数和时间常数.根据(1) 式，若理想梯度场p的波形为${{G}_{p}}(t)$，则在涡流影响下，磁体空间中产生的涡流${{G}_{e}}(t)$可以如下计算^[19]：

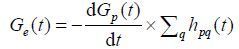
(2)

1.1.2 梯度延时

梯度延时（gradient delay），指实际梯度相对于理论梯度在时序上的延迟^[16]，其作用可以表示为：

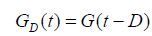
(3)

其中，与分别代表理想梯度波形与延时的梯度波形，D为梯度延时.

梯度延时主要来源于梯度放大器与线圈的响应时间延时^[16].在一定温度下，梯度延时可以被视为一个常数；而温度变化时，则可能会发生变化.由于梯度延时的存在，脉冲序列中的梯度事件总是相对于射频脉冲和采样略有滞后.在笛卡尔采样体系下，梯度延时在层选方向上造成层面回聚不完全，使得k空间数据在层面梯度方向上出现偏移；在编码梯度方向上，梯度延时引起回波中心的偏移，在图像域上主要表现为线性相位.因此，在一般的自旋回波成像和梯度回波成像上，梯度延时并不会造成伪影，其影响可以忽略不计.在射线采样模式的UTE方法中（如图 1所示），梯度延时在层面上的影响与笛卡尔采样相同，在编码梯度方向上，梯度延时将导致采样最初的若干点停留在k空间原点.射线轨迹滞后，如不加以校正，将引起网格化重建时的网格化错误.另外，和常规序列相比，UTE序列针对超快弛豫的组织成像，通常需要更高的采样率和更小的采样时间间隔，从而更加剧了梯度延时引起的k空间轨迹失真.

1.2 k空间轨迹失真的校正 1.2.1 涡流测量

涡流测量的脉冲序列如图 2所示^[20]：在梯度脉冲后，间隔一个可变延时△，用硬脉冲激发样品，采集FID信号并用△t时间内的相位演化来表征涡流.逐次改变延时△，重复测量，得到涡流随时间的衰减曲线，然后用多指数拟合算法即可大致确定涡流的时间常数和幅度常数.

在实验中，梯度脉冲的时间应足够长，以保证梯度前沿引起的涡流衰减完全.理论上，为测量涡流的冲激响应，测试梯度应为一矩形梯度，实际中零边沿时间无法实现.但一般而言，边沿时间对测量结果的影响很小^[18]，在测量中使其尽可能短即可.涡流测试样品一般选择一个球形对称的均匀样品，T₁与T₂均适中，以保证信号具有足够的信噪比并能及时恢复到平衡态.

涡流测量的基本原理如下，以Z梯度为例，将对称样品在Z轴上放置，在共振条件下，FID信号的相位为：

(4)

其中t代表时间；τ是积分变量；$\Delta {{B}_{0}}$为零阶涡流；${{G}_{e}}$为一阶涡流；z为样品在梯度方向上的偏置距离；${{\phi }_{0}}$是与涡流无关的相位（如场不均匀性引起的相位、接收相位等）.

对于零阶涡流，将对称均匀样品置于磁场中心，(4) 式右边第二项消去，为消除无关相位${{\phi }_{0}}$的影响，可以在关闭梯度条件下测量一个FID作为相位参考信号，其相位与${{\phi }_{0}}$相等.

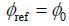
(5)

则由零阶涡流引起的信号相位为：

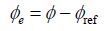
(6)

零阶涡流可近似为：

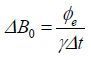
(7)

对于一阶涡流，将样品偏离中心放置，FID信号相位包含了零阶涡流、一阶涡流和${{\phi }_{0}}$三部分的贡献.首先，按照(5) 式和(6) 式消除涡流无关相位的影响；再减去以样品处于中心时测量到的零阶涡流引起的相位，即可得到由一阶涡流引起的相位.一阶涡流近似为：

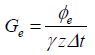
(8)

1.2.2 k空间轨迹测量

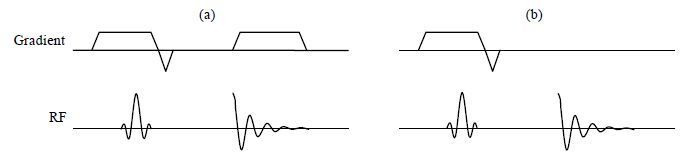
k空间轨迹的测量使用如图 3所示的脉冲序列^[14].以Z梯度为例：首先，Z方向上的层选梯度与选择性脉冲激发一个偏中心的薄切片；然后开启测试梯度并同时采集FID信号，如图 3(a)所示.为消除层选梯度和场不均匀性等其他因素对信号相位的影响，在关闭测试梯度的条件下采集一个相位参考信号，如图 3(b)所示.理论上，两个信号的相位差为：

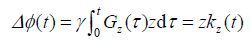
(9)

其中z为层面偏中心的距离；${{k}_{z}}(t)$为k空间轨迹的Z分量；X和Y分量的测量方法与此类似.${{k}_{z}}(t)$中包含了梯度延时和梯度涡流的贡献，因此，(9) 式更为准确的写法为：

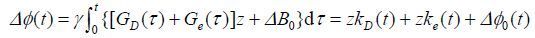
(10)

${{k}_{D}}(t)$为延时影响下的k空间轨迹，当使用梯形梯度时，${{k}_{D}}(t)$的解析式很容易计算，其结果可查阅参考文献^[14]；第二、三项分别为一阶和零阶涡流引起的相位演化.

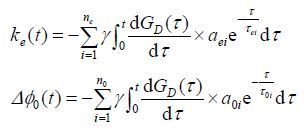
(11)

n_e和n₀分别代表一阶涡流和零阶涡流的项数；a_ei 、${{\tau }_{ei}}$分别为第i项一阶涡流的幅度常数和时间常数；${{a}_{0i}}$、${{\tau }_{0i}}$分别为第i项零阶涡流的幅度常数和时间常数.

1.2.3 参数优化

在1.2.1节，通过NMR实验测量了涡流曲线，并得到了涡流常数的大致数值.而1.2.2节则说明了测量k空间轨迹的方法，并给出了轨迹曲线的数学模型.MRI系统的真实梯度延时和涡流常数应满足以下两个条件：

（1）按照(10) 式估计的k空间应逼近测量的k空间；

（2）按照(1) 式计算的涡流响应曲线应逼近测量的涡流曲线.

因此，梯度延时与涡流常数的求解可以表示为如下约束多目标优化问题：

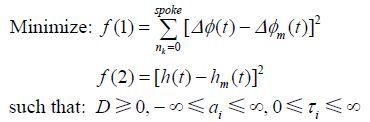
(12)

其中spoke为射线条数，对n_k的求和表示对UTE序列整个k空间轨迹的综合考虑；$\Delta \phi (t)$与$\Delta {{\phi }_{m}}(t)$分别代表按照(10) 式估计的k空间轨迹曲线与测量的轨迹曲线；$h(t)$与${{h}_{m}}(t)$分别为按(1) 式估计的涡流响应曲线与实际测量的涡流曲线.在优化过程中，梯度延时的初始值设为0（或者更准确地，可以先用示波器测量得到一个大概值），而涡流的初值可以设为1.2.1节中拟合的涡流常数.在图像重建时，零阶涡流通过对FID进行相位校正来补偿，而一阶涡流和梯度延时则通过校正k空间轨迹来进行补偿.

2 仪器与试剂

脉冲序列及相关实验在Bruker 4.7 T小动物超导MRI系统上实现.梯度涡流、梯度延时测量的样品为CuSO₄水溶液（浓度为1.96 g/L），T₁约为110.2 ms，T₂约为74.8 ms.

样品保存在一个直径为40 mm的塑料球体中，并用一维梯度实验进行样品定位.结构水模样品（CuSO₄·2H₂O，浓度为1 g/L；Agar，浓度为10 g/L）的T₁约为245.6 ms，T₂约为51.8 ms.超短T₂时间样品为4种不同浓度的MnCl₂溶液，保存在5 mL比色瓶中、各支编号、浓度及T₂见表 1所示.

3 结果与讨论 3.1 梯度涡流测量

梯度涡流的测量结果如图 4所示.图 4(a)~(c)分别为X/Y/Z梯度的一阶涡流，其中Y梯度的一阶涡流包含两个主要的指数项，X/Z梯度的一阶涡流仅包含一个主要的指数项；图 4(d)为Z梯度的零阶涡流.X/Y梯度的零阶涡流非常小，此处予以忽略.涡流测量的参数如下：梯度时间为10 ms，梯度强度为80 mT/m，可变延时D以5 ms为间隔均匀分布在0~1 ms之间，编码时间Dt为2 ms，硬脉冲脉宽为20 ms.

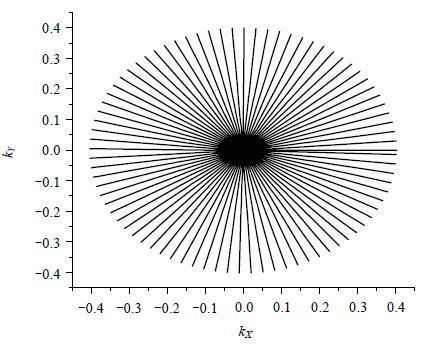
3.2 k空间轨迹曲线测量

k空间轨迹曲线的测量结果如图 5所示，这里以X、Y作读梯度为例（Z梯度的测量与之类似）.其中k空间频率已归一化到-0.5~0.5之间.为了清晰显示，图 5仅画出了其中1/10的射线轨迹数据.测量参数如下：采样频率为200 kHz，视野（FOV）为80 mm×80 mm，采样矩阵为256×256，层厚为0.5 mm，层偏为10 mm.

3.3 梯度延时与涡流优化参数

根据测量得到的涡流曲线和k空间轨迹，用(12) 式优化计算出各通道梯度延时及其涡流的幅度常数，其结果见表 2.

3.4 真实k空间轨迹估算

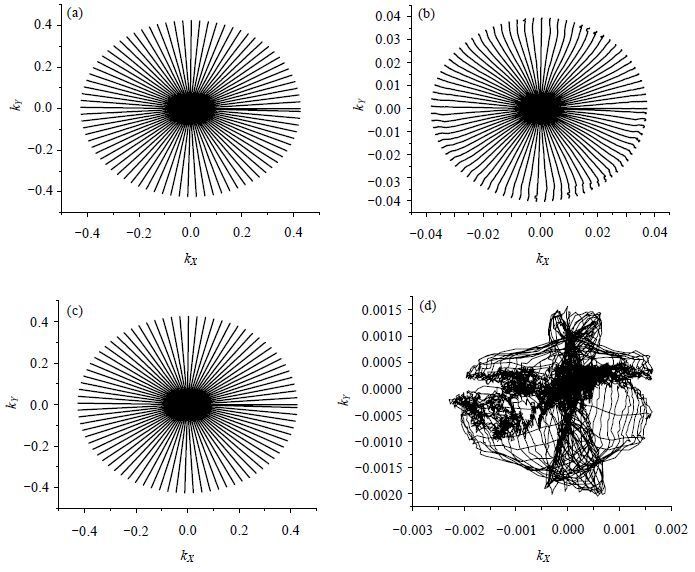
确定了梯度系统的涡流与延时之后，按照(5) 式和(6) 式即可估计真实的k空间轨迹，而无需在每次实验前都重新测量轨迹.用这种方法估计k空间的一个例子如图 6所示.图 6(a)为校正前的k空间轨迹图，图 6(b)为校正前k空间轨迹与测量k空间之间的误差图，图 6(c)为按照表 2中的涡流和延时估计的k空间轨迹图，图 6(d)为估计的k空间轨迹图与测量k空间图之间的误差图.可以看出，经过轨迹校正后，k空间轨迹的误差明显减小.

用此方法进行k空间轨迹校正的实际应用的结果如图 7、8所示.UTE图像的重建使用双倍网格化算法，卷积核为Kaiser-Bessel窗（常数b取6.486 1），窗宽为3，点数为64.图 7(a)~(c)分别为水模的常规自旋回波（spin echo，SE）图像以及利用轨迹校正前后的UTE图像.SE的TE为14 ms，UTE序列的TE为0.475 ms.其余主要参数二者相同：采样频率为50 kHz，FOV为80 mm×80 mm，采样矩阵为256×256，层厚为2 mm.可以看到，k空间轨迹校正前，图像存在明显伪影，而校正后的图像质量则大幅改善，细节已经非常接近SE图像.图 8为超短T₂样品的UTE和常规梯度回波（gradient refocused echo，GRE）图像.UTE序列的TE为0.475 ms，采样频率为120 kHz；GRE的TE为6 ms，采样频率为50 kHz.其余的主要参数二者相同：FOV为80 mm×80 mm，采样矩阵为256×256，层厚为2 mm.在图 8(b)的GRE图像中，T₂较长的1号样品清晰可见，2号样品信号的衰减已经十分明显，3、4号样品则完全不可见；校正前的图 8(c)已被伪影所湮没，而在校正后的图 8(d)中则可以清晰地观察到所有样品管的图像.

以上实验表明，这种k空间轨迹估计的方法可以明显地减轻UTE成像中轨迹失真带来的伪影问题.经过轨迹校正后的UTE图像，可以很好地呈现快速弛豫组织图像，并能够几乎完整地恢复图像细节.这种轨迹校正方法不需要在每次实验前额外地测量k空间轨迹，可以成倍地降低UTE采样和重建的时间.

4 结论

本文提出了一种改进的k空间轨迹校正方法：以最小化k空间轨迹误差和涡流曲线误差作为目标函数，求解多目标优化问题，从而确定MRI系统的梯度延时和残余涡流的幅度常数、时间常数，再以之对k空间轨迹进行校正.该方法便于实现且时效性高，能有效减轻UTE成像中轨迹失真引起的图像伪影.