文章信息
- 宋阳, 谢海滨, 杨光
- SONG Yang, XIE Hai-bin, YANG Guang
- 用于压缩感知磁共振成像的分割字典学习算法
- Dictionary Learning with Segmentation for Compressed-Sensing Magnetic Resonance Imaging
- 波谱学杂志, 2016, 33(4): 559-569
- Chinese Journal of Magnetic Resonance, 2016, 33(4): 559-569
- http://dx.doi.org/10.11938/cjmr20160405
-
文章历史
收稿日期: 2015-12-31
收修改稿日期: 2016-10-24


DOI:10.11938/cjmr20160405
2. 上海卡勒幅磁共振技术有限公司, 上海 201614
2. Shanghai Colorful Magnetic Resonance Technology Co. Ltd., Shanghai 201614, China
磁共振成像(MRI)技术是医学影像中常用的技术之一,具有无电离辐射、软组织对比度好、任意角度成像等优势.限制MRI应用的主要瓶颈之一是其扫描时间较长,主要原因是MRI技术需要对图像的傅里叶变换域,即k空间进行全采样.在典型的二维图像扫描中,假设每次射频激发只采集一个回波,则总扫描时间可以简单表示为:
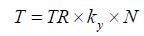
|
(1) |
其中TR是射频脉冲间隔时间,是相位编码次数,N是累加次数.可见总采样时间与相位编码次数成正比,因此可以通过减少相位编码次数加速磁共振信号的采集.
常用的利用减少相位编码次数而加速采样的技术包括并行成像(Parallel-MRI)技术[1]、部分傅里叶成像(Partial Fourier MRI)技术[2],以及近年来出现的压缩感知(Compressed Sensing)方法[3-6].并行成像技术可以充分利用多通道线圈在空间灵敏度分布的不同,对k空间进行等间隔欠采,之后用重建算法对图像进行去卷褶,得到较好的重建图像.使用如自校准并行采集(GeneRalized Autocalibrating Partially Parallel Acquisition, GRAPPA)[7]和基于灵敏度编码(SENSitivity Encoding, SENSE)[8]等并行采集方案,能够缩短一半的采样时间.部分傅里叶成像技术利用k空间的共轭对称性,来减少相位编码步的采集.由于实际采集数据中存在相位误差,应用中需要结合相位校正,一般只减少k空间中高频信息的采集.而压缩感知可以通过非均匀随机采样的方式,大幅度减少相位编码次数,将含有非相干伪影的磁共振图像进行某种变换,进行稀疏重建,最终得到与全采k空间的图像相近的重建图像.将压缩感知技术应用在MRI中,可以大大减少采样时间、加快扫描速度,同时可以与其他快速成像技术相结合,进一步缩减磁共振扫描时间.
磁共振图像进行压缩感知重建需要使用稀疏性作为约束条件,这就要求将图像通过小波变换、有限差分等变换到稀疏域[9].字典学习(Dictionary Learning,DL)可以根据数据自身训练出适用于该数据的基的集合,该集合称为字典,而用自身训练出的字典进行变换可以得到更好的稀疏性,得到更优的压缩感知重建图像[5].在基于字典的稀疏表达下,可以基于图像块的信息进行字典学习[14, 15],也可以结合已有的稀疏变化[16],或根据磁共振图像自相似信息[18],进行稀疏字典的构建.
在典型的磁共振图像中,感兴趣区域(Region Of Interest, ROI)中包含的组织数量有限,且不同组织的信号间存在一定的对比,可以根据图像的灰阶对图像进行分割.本文利用该特点对传统字典学习算法进行改进,在构建字典之前对图像进行聚类分割[19],并将同一分类的体素的强度设置为相同的灰度值,即对灰阶进行正则化.借此构建出更具有磁共振图像特征的字典.用这样构造出来的字典进行压缩感知图像重建,提升重建图像的质量.
1 算法原理 1.1 传统字典学习算法传统字典学习算法的主要思想是图像分块,从大量的图像块中提取主要特征,训练出适用于该图像的字典.通过迭代优化算法更新字典中每一个基,使得图像中的每一个图像块都可以用字典中少数基的线性组合来近似表示.迭代优化的目标函数可以表示为:
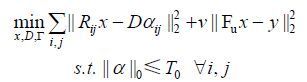
|
(2) |
(2) 式第一项中,x表示要重建出的图像,R表示从图像中提出图像块的操作,D是构建的字典,a是用字典对图像块进行稀疏表达的系数,G表示a的集合,即稀疏表达系数;第二项中Fu表示对图像做傅里叶变换并进行欠采,y表示欠采得到的k空间数据,v是权重常数.其中更新字典D使用K-SVD算法[22],更新a用OMP算法[21],该迭代过程可以表示为:
| 字典学习算法: |
|
1. 欠采k空间数据经傅里叶变换获得初始图像x0,迭代次数N,i=0
2. 当i<N或 k空间数据的差异小于e的时候,则停止迭代. a) 提取图像块用SVD得到初始字典; b) 用K-SVD算法训练并更新字典Di; c) 用OMP算法进行稀疏编码,更新ai; d) 得到重构图像,更新xi; e) k空间保真,更新xi; f) i=i+1; 3. 输出图像xi. |
分割字典学习(Dictionary Learning with Segmentation, DLS)算法的主要特点是在利用图像进行字典训练之前,使用k-means聚类算法[24],对图像进行聚类分割,并用每个分类的灰度均值替代该类所有像素点的灰阶值,并用处理后的图像训练字典.具体算法过程如下:
| 分割字典学习算法: |
|
1.欠采k空间数据经傅里叶变换获得初始图像x0,设置迭代次数N,聚类数M,i=0 2.当i<N或 k空间数据的差异小于e的时候,则停止迭代. a) 对初始图像进行分割操作,利用分割结果对图像进行正则化; b) 提取图像块并得到初始字典; c) 用K-SVD算法训练并更新字典Di; d) 用OMP算法进行稀疏编码,更新ai; e) 得到重建图像,更新xi; f) k空间保真,更新xi; g) i=i+1; 3.输出图像xi. |
实验所用计算机模拟数据如图 1(a)所示(该数据在Matlab 2015a平台下进行模拟).原始模型分辨率为4 096×4 096,其中圆型结构的直径从上到下分别为:16、32、48、80、160.对该模型数据进行傅里叶变换获得k空间数据,取中央512×512的区域作为实验的全采图.
对k空间进行伪随机欠采,欠采模板如图 1(b)所示,总采样率为40%,其中中央连续采样10%,欠采的k空间在非采样位置用0填充,傅里叶变换得到稀疏采样的重建图像[图 1(d)].为了比较,采集k空间中央40%的数据并在周围填0,重建图像如图 1(c)所示.图 1(e)和图 1(f)是以图 1(d)为初始图像,分别进行传统字典学习和分割字典学习算法重建的结果.

|
| 图 1 (a) 全采的金标准图像.(b) k空间欠采模板,采样率为40%,其中中央连续采样10%.(c) k空间中央连续采集40%重建图像. (d) 按照(b)的欠采模板对k空间进行采样,其余填0的傅里叶变换稀疏采样重建图像. (e) 以(d)为初始图像使用传统字典学习算法的重建图像.(f) 以(d)为初始图像使用分割字典学习算法的重建图像 Fig. 1 (a) Ground-truth image. (b) Sampling mask: 40% sampling rate with 10% center fully sampled (c) Fourier transform of zero-padded k-space with 40% center fully sampled. (d) Fourier transform of zero-filled k-space sampled by mask (b). (e) Image reconstructed with DL from (d). (f) Image reconstructed with DLS from (d) |
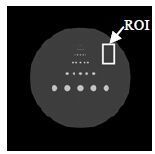
为了评价图像的重建效果,在各重建图像中的相同的均匀区域划出一个感兴趣区域进行灰度值统计分析,计算该区域中的平均值和标准差,数值如表 1所示.由于数据在4 096×4 096尺度上模拟.k空间中央采集512×512之后会在图像域中出现明显的吉布斯震荡,因此导致了全采图像感兴趣区域的标准差不为0.横向比较发现,分割字典学习算法得到的图像,与其他重建图像相比,在均值相差不大的情况下,标准差最低,即图像的吉布斯震荡得到了有效的抑制.
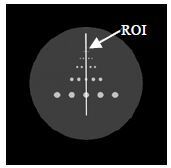
为了评价算法还原细节的能力,我们测量了重建图像中圆形区域的半高宽[24].从表 2中我们可以发现,分割字典学习算法估计出的半高宽与全采图像最为相似,在半高宽的计算上优于传统的字典学习算法,说明本文算法在细节还原方面表现较好.
 | 全采图像 | 中央采40%填0 | 稀疏采样40%填0 | 传统字典学习算法 | 分割字典学习算法 | |
| 均值 | 599.54 | 599.52 | 599.54 | 599.58 | 599.50 | |
| 标准差 | 1.79 | 2.28 | 6.36 | 3.41 | 2.71 |
 | 全采图像 | 中央采40%填0 | 稀疏采样40%填0 | 传统字典学习算法 | 分割字典学习算法 |
| 1.63 | 1.64 | 1.81 | 1.65 | 1.60 | |
| 3.76 | 2.91 | 3.40 | 3.37 | 3.41 | |
| 5.89 | 5.18 | 8.30 | 5.51 | 5.79 | |
| 9.85 | 9.26 | 9.44 | 9.51 | 9.73 | |
| 19.92 | 19.20 | 19.33 | 19.43 | 19.87 | |
| *直线标注中从上到下分别对应于图中从上到下不同尺度的结构 | |||||
使用BrainWeb[25](http://brainweb.bic.mni.mcgill.ca/brainweb/)的数据进行模拟实验,数据生成使用T2加权脉冲序列,层厚为1 mm,噪声水平为0.采用一维非均匀随机采样,采样率为35%,其中k空间中心连续采样15%.对重建图像进行定量评价,评价参数使用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)、高频误差范数(High Frequency Error Norm, HFEN)[5]和结构相似性(Structure Similarity, SSIM)[25]进行评价.其中PSNR从像素角度整体评价重建图像;HFEN利用高频信息,从组织边缘和细节处进行评价;SSIM从结构相似性方面对图像进行评价.
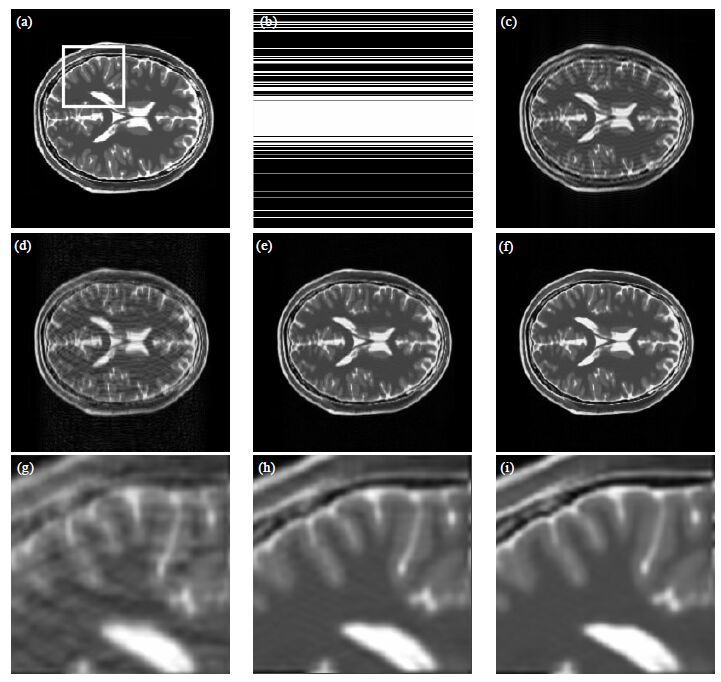
该实验将字典学习算法与分割字典学习算法设置相同的重建参数,在无添加噪声,相同采样模板进行比较实验.图 2为填0重建、传统字典学习重建和分割字典学习重建结果.结果表明跟传统字典学习算法(PSNR= 27.52,HFEN= 386.9,SSIM= 0.573)相比,利用分割字典重建算法在PSNR(PSNR= 31.53)、HFEN(HFEN= 216.8)、SSIM(SSIM= 0.612)方面均可以得到更好的结果.视觉上,利用分割字典学习算法重建的图像伪影更小,也有效地消除了吉布斯震荡.
|
| 图 2 (a) k空间全采的模图.(b) k空间欠采模板,采样率为35%,其中中央连续采15%.(c) k空间连续采集35%重建图.(d) 按照(b)的欠采模板对k空间进行采样,其余填0的重建图.(e)和(f)分别为传统字典学习算法和分割字典学习算法对按照(b)图模板得到的欠采数据进行重建的结果图像.其中传统字典学习算法重建图像的PSNR=27.52,SSIM=0.573,HFEN=386.9;分割字典学习算法重建图像的PSNR=31.53,SSIM=0.612,HFEN= 216.8.(g)~(i)图为(d)~(f)的细节放大,细节区域在(a)中用方框标出 Fig. 2 (a) The magnitude image from full sampled k-space. (b) The sampling mask: 35% sampling rate with 15% center. (c) The reconstruction from k-space with 35% center and outer zero-filled. (d) The reconstruction from k-space sampled by mask (b). (e) The reconstruction using DL from (d). (f) The reconstruction using DLS from (d). The quantitative evaluation of DL: PSNR=27.52, SSIM=0.573, HFEN=386.9. The quantitative evaluation of DLS: PSNR=31.53, SSIM=0.612, HFEN=216.8. (g)~(i) Zoom in the region of interest which is marked as square in (a) and show the details of (d)~(f) |
使用上海卡勒幅磁共振技术有限公司的Sapphire 1.5 T的超导MRI系统,扫描线圈为4通道头部线圈,扫描序列为自旋回波序列,扫描参数为:观察视野(FOV)=240 mm ×240 mm,层厚(slice thickness)= 6 mm,层数(slices)= 16,回波时间(TE)= 15 ms,重复时间(TR)= 420 ms,采样矩阵(matrix)= 512×512,其中相位编码方向采用35%伪随机欠采,中央连续采集15%.
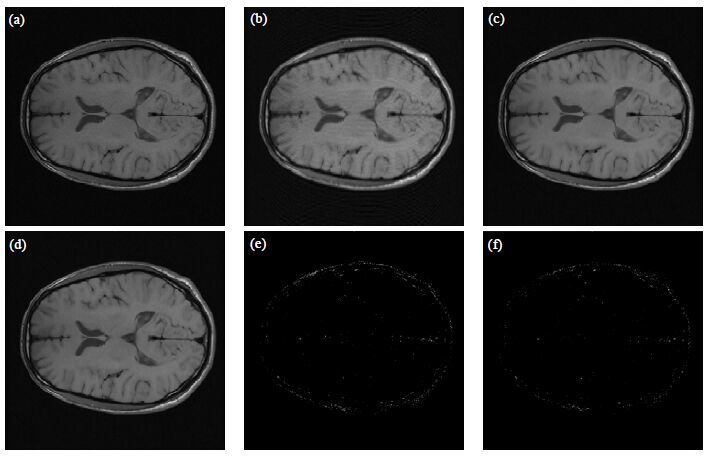
传统字典学习和分割字典学习算法虽然都可以给出较好的重建结果,但其差别主要体现在边缘部分的强度上,因此图 3中的HFEN和SSIM两者相差不大(传统字典学习算法:HFEN = 256.6,SSIM = 0.631;分割字典学习算法:HFEN = 221.4,SSIM = 0.632);但分割字典学习算法更好地抑制了噪声,使得PSNR有显著提高(传统字典学习算法:PSNR = 29.14;分割字典学习算法:PSNR = 32.08).
|
| 图 3 真实数据在35%欠采模式下进行重建实验.(a) 全采图;(b) 35%欠采模式下填0的重建图;(c) 以(b)为初始图像使用传统字典学习算法的重建图;(d) 以(b)为初始图像使用分割字典学习算法的重建图;(e)、(f)是重建图(c)、(d)与全采图(a)的差值,为了显示差异而进行了窗宽窗位的调节.其中传统字典学习算法重建图像的PSNR=29.14,SSIM=0.631,HFEN=256.6,分割字典学习算法重建图像的PSNR=32.08,SSIM=0.632,HFEN=221.4 Fig. 3 The in-vivo experiment. (a) The image from full sampled k-space. (b) The reconstruction from under-sampled k-space with 35%. (c) The reconstruction by DL from (b): PSNR=29.14, SSIM=0.631, HFEN=256.6. (d) The reconstruction by DLS from (b): PSNR=32.08, SSIM=0.632, HFEN=221.4. (e) The difference between DL and the full sampled image. (f) The difference between DLS and the full sampled image |
对在同样欠采模式下得到的初始图像进行字典学习,分割字典学习算法由于加入了聚类分割,学习所得的字典也很不相同.图 4显示了第一次迭代过程中用K-SVD算法进行字典学习得到的字典图像.图像进行分割并按照分割结果进行灰阶正则化后进行K-SVD训练字典,相比传统字典学习算法,分割字典学习算法得到的字典会包含结构简单而更像图像细节的基,由此进行稀疏表达会得到更加稀疏的结果.

|
| 图 4 第一次迭代中训练所得的字典.(a) 分割字典学习算法;(b) 传统字典学习算法 Fig. 4 The trained dictionary in the first iteration of (a) DLS and (b) DL |
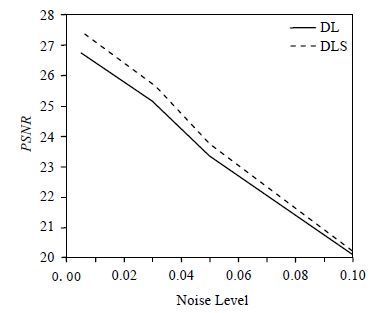
对BrainWeb上的无噪声数据添加高斯分布的复数噪声,其均值为0,方差分别为图像域最大值的0.5%、1%、3%、5%、10%.采用35%的随机欠采(中央连续采集15%),分别用传统字典学习与分割字典学习两种算法进行重建,并计算各自重建图像的PSNR.为了结果的可靠性,每个噪声水平下进行10次独立的实验,将10次实验PSNR的平均值作为最终结果.由图 5可以看出,随着噪声水平的提高,图像重建质量逐渐下降,但引入分割字典学习可以得到比传统字典学习算法获得更好的重建质量.
|
| 图 5 两种算法重建图像PSNR随噪声水平的变化曲线 Fig. 5 Changes of PSNR of the reconstructed images with the changes of noise level |
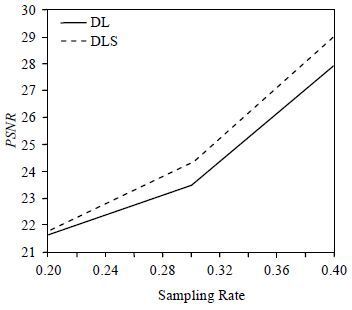
为了评价本文算法在不同采样率下的表现,我们利用前述无噪的BrainWeb图像作为金标准,采用20%、30%、40%的伪随机欠采,其中中央连续采样10%,比较了分割字典学习与传统字典学习的PSNR.每种采样率进行10次独立实验,参数保证相同,分辨计算每次重建图像的PSNR、HFEN和SSIM等评价参数,求平均值进行统计分析,其中PSNR随不同噪声水平的变化曲线如图 6所示.由图可以看出,图像质量随着采样率的提高在增长,在各个采样率下,分割字典学习算法都可以获得比传统字典学习算法更优的重建质量.
|
| 图 6 两种算法重建图像PSNR随采样率的变化曲线 Fig. 6 Changes of PSNR of the reconstructed images with the changes of sampling rate |
分割字典学习算法比传统字典学习算法多引入了一个聚类分割参数,而该参数设置对于算法的重建质量有重要影响.以BrainWeb图像为例,聚类分割参数分别设置为2、3、4、5、6进行独立实验,相位编码方向进行随机欠采,采样率35%,中央连续采样10%.由表 3可以看到,在参数设置为4时,可以取得最优的重建效果,这也对应于图像中的灰质、白质、组织液、背景区域4个灰阶部分,因此可以获得较优的重建质量.这一结果意味着在实践中应用分割字典学习算法时,可能需要根据扫描部位的不同来设置不同的分割参数以达到最佳的图像重建效果.
| 分割参数 | 2 | 3 | 4 | 5 | 6 |
| PSNR | 27.64 | 28.21 | 29.28 | 28.83 | 28.59 |
本文在传统的字典学习框架下针对磁共振图像特点的进行改进,在构建特征字典时使用根据组织结构而进行灰阶稀疏处理过的训练数据,使得构建的字典更具磁共振图像的特征,该算法的重建图像质量与传统的字典学习算法相比具有明显提高.本文还讨论了在不同采样率、不同噪声水平下的重建情况,结果显示利用分割字典学习算法均可以得到较好的重建结果.该思想可以在不改变原有算法的基础上针对磁共振图像特点做出优化,并能进一步将其扩展到其他基于字典学习的磁共振图像重建中.
| [1] | Pruessmann K P . Encoding and reconstruction in parallel MRI[J]. NMR Biomed , 2006, 19 (3) : 288-299 DOI:10.1002/(ISSN)1099-1492 |
| [2] | McGibney G, Smith M R, Nichols S T et al . Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI[J]. Magn Reson Med , 1993, 30 (1) : 51-59 DOI:10.1002/(ISSN)1522-2594 |
| [3] | Donoho D L . Compressed sensing[J]. IEEE T Inform Theory , 2006, 52 (4) : 1289-1306 DOI:10.1109/TIT.2006.871582 |
| [4] | Lustig M, Donoho D, Pauly J M . Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med , 2007, 58 (6) : 1182-1195 DOI:10.1002/(ISSN)1522-2594 |
| [5] | Ravishankar S, Bresler Y . MR image reconstruction from highly undersampled k-space data by dictionary learning[J]. IEEE T Med Imaging , 2011, 30 (5) : 1028-1041 DOI:10.1109/TMI.2010.2090538 |
| [6] | Tošić I, Frossard P . Dictionary learning[J]. IEEE Signal Proc Mag , 2011, 28 (2) : 27-38 DOI:10.1109/MSP.2010.939537 |
| [7] | Griswold M A, Jakob P M, Heidemann R M et al . Generalized autocalibrating partially parallel acquisitions (GRAPPA)[J]. Magn Reson Med , 2002, 47 (6) : 1202-1210 DOI:10.1002/(ISSN)1522-2594 |
| [8] | Pruessmann K P, Weiger M, Scheidegger M B et al . SENSE:sensitivity encoding for fast MRI[J]. Magn Reson Med , 1999, 42 (5) : 952-962 DOI:10.1002/(ISSN)1522-2594 |
| [9] | Ma S, Yin W, Zhang Y, et al. Computer Vision and Pattern Recognition[C]. Anchorage Alarke:IEEE, 2008. |
| [10] | Qu X B, Zhang W R, Guo D et al . Iterative thresholding compressed sensing MRI based on contourlet transform[J]. Inverse Prob Sci Eng , 2010, 18 (6) : 737-758 DOI:10.1080/17415977.2010.492509 |
| [11] | Zheng Hui(郑慧), Han Ming-yue(韩明月), Hu Bing-wei(胡炳文) et al . Comparison of different sampling schemes in compressed sensing reconstruction for DQ-SQ experiments(不同采样模式的固体DQ-SQ实验的压缩感应重建比较)[J]. Chinese J Magn Reson(波谱学杂志) , 2014, 31 (4) : 535-547 |
| [12] | Han Ming-yue(韩明月), Zheng Hui(郑慧), Hu Bing-wei(胡炳文) et al . Compressed sensing reconstruction with iterative soft thresholding for two-dimension solid state NMR spectra with broad peaks(迭代软阈值法压缩感知重建谱峰较宽的二维固体谱)[J]. Chinese J Magn Reson(波谱学杂志) , 2015, 32 (4) : 551-562 |
| [13] | Kim Y, Altbach M I, Trouard T P, et al. Compressed sensing using dual-tree complex wavelet transform[C]. Proc ISMRM, 2009. |
| [14] | Aharon M, Elad M, Bruckstein A . K-SVD:An algorithm for designing overcompletedictionaries for sparse representation[J]. IEEE T Signal Process , 2006, 54 (11) : 4311-4322 DOI:10.1109/TSP.2006.881199 |
| [15] | Zhan Z F, Cai J F, Guo D et al . Fast multi-class dictionaries learning with geometrical directions in MRI reconstruction[J]. IEEE T Biomed Eng DOI:10.1109/TBME.2015.2503756,2015 |
| [16] | Lai Z Y, Qu X B, Liu Y S et al . Image reconstruction of compressed sensing MRI using graph-based redundant wavelet transform[J]. Med Imag Anal , 2016, 27 : 93-104 DOI:10.1016/j.media.2015.05.012 |
| [17] | Qu X B, Guo D, Ning B D et al . Undersampled MRI reconstruction with patch-based directional wavelets[J]. Magn Reson Imag , 2012, 30 (7) : 964-977 DOI:10.1016/j.mri.2012.02.019 |
| [18] | Qu X B, Hou Y K, Lam F et al . Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator[J]. Med Imag Anal , 2014, 18 (6) : 843-856 DOI:10.1016/j.media.2013.09.007 |
| [19] | Clarke L P, Velthuizen R P, Phuphanich S et al . MRI:stability of three supervised segmentation techniques[J]. Magn Reson Imag , 1993, 11 (1) : 95-106 DOI:10.1016/0730-725X(93)90417-C |
| [20] | Clarke L P, Velthuizen R P, Camacho M A et al . MRI segmentation:methods and applications[J]. Magn Reson Imag , 1995, 13 (3) : 343-368 DOI:10.1016/0730-725X(94)00124-L |
| [21] | Singh M, Patel P, Khosla D et al . Segmentation of functional MRI by K-means clustering[J]. IEEE T Nucl Sci , 1996, 43 (3) : 2030-2036 DOI:10.1109/23.507264 |
| [22] | Tropp J A . Greed is good:Algorithmic results for sparse approximation[J]. IEEE T Inform Theory , 2004, 50 (10) : 2231-2242 DOI:10.1109/TIT.2004.834793 |
| [23] | Hartigan J A, Wong M A . Algorithm AS 136:A k-means clustering algorithm[J]. J Appl Stat , 1979, 28 (1) : 100-108 DOI:10.2307/2346830 |
| [24] | Brown R W, Cheng Y C N, Haacke E M et al . Magnetic resonance imaging:physical principles and sequence design[M]. USA: John Wiley & Sons, 2014 . |
| [25] | Cocosco C A, Kollokian V, Kwan R K S et al . BrainWeb:Online interface to a 3D MRI simulated brain database[J]. NeuroImage , 1997, 5 (4) : s425 |
| [26] | Wang Z, Bovik A C, Sheikh H R et al . Image quality assessment:from error visibility to structural similarity[J]. IEEE T Image Process , 2004, 13 (4) : 600-612 DOI:10.1109/TIP.2003.819861 |

本作品采用知识共享署名 4.0 国际许可协议进行许可。
 2016, Vol. 33
2016, Vol. 33



