文章信息
- 庄孝星, 马崚嶒, 蔡聪波, 陈忠
- ZHUANG Xiao-xing, MA Ling-ceng, CAI Cong-bo, CHEN Zhong
- 一种基于时空变换和压缩感知的磁共振螺旋采样的图像重建算法
- An Image Reconstruction Algorithm for Spiral MRI Based on Spatio-Temporal Transform and Compressed Sensing
- 波谱学杂志, 2016, 33(4): 549-558
- Chinese Journal of Magnetic Resonance, 2016, 33(4): 549-558
- http://dx.doi.org/10.11938/cjmr20160404
-
文章历史
收稿日期: 2016-04-08
收修改稿日期: 2016-10-24


DOI:10.11938/cjmr20160404
磁共振成像(Magnetic Resonance Imaging, MRI)在软组织检测成像中具有独特的优势,相比于电子计算机断层扫描(Computed Tomography,CT)等成像方法,MRI具有高分辨力和无放射损伤等优点,可以用来观察非常多样的生物组织[1].MRI采集到的数据可以视为磁共振图像在傅里叶域的数据[2],也称为k空间数据.实验通过采集足够的k空间数据量来获得合适的空间分辨率.多扫描序列通过多次激发射频(Radio Frequency,RF)脉冲,每次脉冲后采集一行数据来遍历k空间的整个矩形区域.每次RF脉冲后都需要一段弛豫时间,因此消耗的时间比较长.冗长的弛豫时间限制了磁共振多扫描序列在临床医学的应用.相比于多扫描序列,快速采样序列一次RF脉冲激发就可以采集k空间整个矩形区域的数据,结合傅里叶变换能够快速重建图像.经典的快速序列方法是平面回波成像(Echo Planar Imaging,EPI).它在一次激发后,采用正负梯度切换的方式来遍历k空间的整个矩形区域.但是EPI采集到的信号是低分辨的,且对不均匀场非常敏感,重建的图像经常伴随着扭曲和伪影.
螺旋采样是一种高速的数据采集策略,已经广泛应用到功能性成像、并行成像和动态成像等各种快速成像技术中.该采样方式具有许多优点,它不仅梯度功率的利用效率高、成像速度快[3],而且对流动和运动伪影不敏感,对不均匀场也有着天然的抵抗性[2].螺旋采样的采集轨迹是从k空间的低频区域开始,呈螺旋状向外扩展.螺旋采样的采样轨迹有众多方案.从形状上分类,有方形螺旋采样和圆形采样;从扩展速度上分类,有等角速度和等线速度;从轨迹数量分类,有单螺旋轨迹和多螺旋轨迹并行成像[3-5].
网格化的k空间数据通常可以用傅里叶变换,基于傅里叶变换的最小二乘法,或者压缩感知(Compress Sensing,CS)最优化模型等方法来重建图像.但是螺旋采样的k空间数据并不是分布在均匀的网格点上,也就无法直接使用快速傅里叶变换来重建图像.目前,常见的螺旋采样重建方法是将螺旋状分布的k空间数据映射到笛卡尔坐标系下均匀网格点上,然后再进行快速傅里叶变换重建图像.其中映射方式是指用卷积核函数来插值和滤波[6].比较著名的以网格化和核函数为基础的重建算法有KB(Kaiser Bessel)[7]和非均匀傅里叶变换(Non-Uniform Fast Fourier Transform,NUFFT)[8, 9].然而采用核函数方法的缺点在于这种方法对核函数的依赖性很强,对于不同图像、不同核函数的效果差异比较大.
压缩感知与欠采样的结合是一种快速成像策略.压缩感知首先是由Candès[10]和Donoho[11]等科学家于2004年提出的.压缩感知内在理论是如果信号是可压缩的,那么信号就可以用更少量的数据来表示.压缩感知理论表明如果图像在一个字典下的系数是稀疏的,且图像的采集矩阵与该字典的相干性足够小,就能够以低于Nyquist采样率的数据量来重建图像.大部分医学图像在小波变换、差分变换等变换后是非常稀疏的,这意味着我们只需要采集适量的信号而不需要采集全部的信号就可以重建理想的图像.减少采样的数据量不仅仅减少了采样时间,还减轻了不均匀场和运动伪影的影响[12].Lustig等人[13]将压缩感知应用到传统的笛卡尔系采样的磁共振图像重建中,获得了良好的效果.螺旋采样是欠采样的一种天然的实现方法.螺旋采样与压缩感知的结合,对压缩感知的发展和螺旋采样的应用都具有重要意义.螺旋采样、非均匀傅里叶变换和压缩感知的结合的方案已经取得良好的效果[4, 12].
并行计算已经成为一种主流的计算方式.图形处理器(Graphics Processing Unit,GPU)不仅是一个简单的图形驱动器,而且是并行计算的一种有效的实现方式.GPU并行计算的速度主要取决于GPU的主频和流处理器数量(计算核心数量)[14].GPU的计算能力近年来有了显著的提高.另一方面,统一计算设备架构(Compute Unified Device Architecture,CUDA)能够良好地支持NVIDIA显卡并行计算的编程.CUDA由于简单易编写的特性得到许多关注[15].在磁共振图像重建中,有许多领域的算法是高度可并行的.GPU并行计算将加速磁共振图像重建算法的运行.
本文提出的基于时空变换和压缩感知(Spatio-Temporal Transform-Compress Sensing, STT-CS)的螺旋采样图像重建算法主要包括三个内容:一是构造了时间空间变换矩阵和模型,避免了网格化的过程,从而避免了网格化造成的误差;二是构造和求解了基于压缩感知的最优化模型,与欠采样策略结合,能够以较低采样率的数据来重建图像;三是使用GPU并行计算来减少变换矩阵乘法运算时间,使得该算法能够应用到实际的场景中,具有较强的应用价值.结果表明与非均匀傅里叶变换压缩感知(NUFFT-CS)算法比较,STT-CS算法重建误差更低、效果更好.
1 理论描述 1.1 螺旋采样序列和采样模型 螺旋采样轨迹形状类型众多,包括多轨迹、单轨迹、等线速度和方形螺旋等等.以等角速度的单轨迹的螺旋采样方式为例[如图 1(a)所示],采样轨迹从k空间零频中心开始,等角速度螺旋展开.将极坐标系映射到笛卡尔坐标坐标系,得到该螺旋轨迹在y、x两个方向的投影
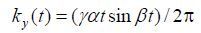
|
(1) |

|
(2) |
其中
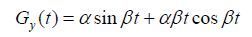
|
(3) |

|
(4) |
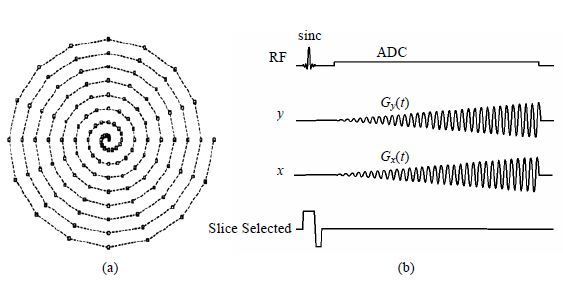
由此可以得到序列图如图 1(b)所示.在施加RF脉冲和层选梯度后,在y、x两个方向施加随时间变化的梯度

|
(5) |
|
| 图 1 磁共振成像等角速度螺旋采样的(a) k空间采样轨迹示意图和(b)等角速度螺旋采样序列示意图 Fig. 1 (a) The k-space trajectory and (b) the sequence of the equal-angular velocity spiral MRI |
为了避免网格化过程带来的误差,本文提出STT-CS模型.它不将数据网格化,而是直接使用采集到的时域信号作为保真约束项,来进行最优化重建.(5) 式表示将空间分布的磁矩图像r(x, y)变换到随时间分布的信号s(t).从空间变换的角度来看,信号从空间域(x, y)变换到了时域(t).因此我们可以构造二维变换矩阵

|
(6) |
大部分医学图像在小波域是稀疏的[13].可以通过求解以下基于压缩感知的约束最优化问题来求解图像

|
(7) |
其中Ψ表示小波变换,α表示磁共振图像变换到小波域的系数.一种求解约束问题的增广拉格朗日形式[16]是

|
(8) |
其中目标函数为

|
(9) |
其中λ和β为模型的常量系数,ν为与α维度相同的中间变量.矩阵右上标H表示共轭转置.
给定α和ν,令(9) 式的微分式

|
(10) |
Ψ选取紧支撑的小波基,因此
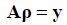
|
(11) |
其中

|
(12) |

|
(13) |
其中
| 初始化 主函数 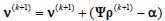 end |
我们在一个数值模型上进行螺旋欠采样的仿真,通过调整参数a、b可以设置每个2p周期内采样点数(Nθ)以及螺旋的圈数(

|
(14) |
其中表示磁共振图像的数值分辨率.以N = 128为例,Nθ为(128, 128) 、(64, 128) 和(64, 64) 对应的采样率分别为100%、50%和25%.
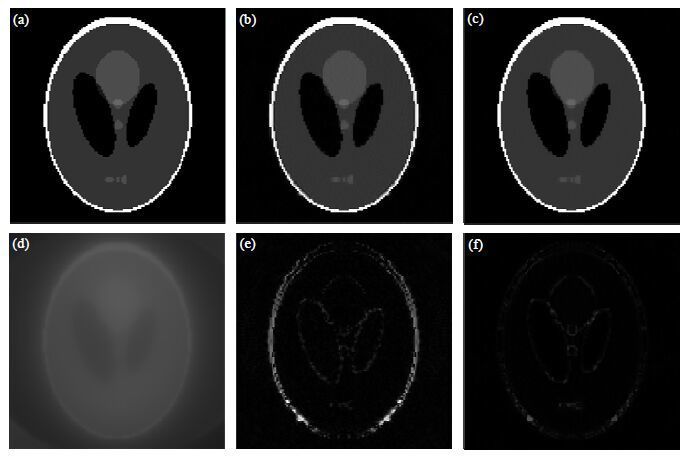
运行STT-CS算法,并与NUFFT-CS算法比较.我们选取了采样率为50%的重建结果展示在图 2中,结果显示,直接使用非均匀反傅里叶变化的图像会存在模糊伪影,NUFFT-CS和STT-CS两种算法都能够良好地去除模糊伪影,重建出图像.而从误差图可以明显看出STT-CS算法的重建误差[图 2(f)]要低于NUFFT-CS [图 2(e)].
|
| 图 2 STT-CS和NUFFT-CS算法的重建结果.(a)参考图像;(b) NUFFT-CS算法的重建结果;(c) STT-CS算法的重建结果;(d)直接非均匀反傅里叶变换的结果;(e) NUFFT-CS算法重建结果的剩余误差;(f) STT-CS算法重建结果的剩余误差.仿真数据是50%欠采样,数值分辨率为128x128 Fig. 2 The reconstruction of STT-CS and NUFFT-CS. (a) Reference image, (b) The reconstruction of NUFFT-CS, (c) The reconstruction of STT-CS, (d) The result of non-uniform inverse fast fourier transformation, (e) The residual error of NUFFT-CS result, (f) The residual error of STT-CS result. The simulation data is 50% under-sampled. The image numeric resolution is 128x128 |
我们还用相对范数误差(Relativel2 Norm Error,RLNE)[17]来量化重建效果.RLNE的表达式为

|
(15) |
其中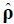
| 采样率/% | RLNE(NUFFT-CS) | RLNE(STT-CS) |
| 25 | 0.201 | 0.082 |
| 50 | 0.119 | 0.030 |
| 100 | 0.097 | 0.018 |
虽然STT-CS算法重建效果良好,但是作为代价,STT-CS算法的复杂度远大于NUFFT-CS.全采样情况下,一次R矩阵乘法运算的复杂度为O(N4).得益于GPU并行计算的发展,计算机的计算能力得到巨大的提升.本算法运行在Window 7 64位系统下,中央处理器(Central Processing Unit, CPU)型号是Core i7(主频3.4 GHz,内存16 GB),显卡型号是NVIDIA GeForce GTX750Ti(主频1 GHz,640核心,内存2 G). 我们分别用CPU和GPU实现了R矩阵乘法运算,并统计了这两种实现方式的在不同数值分辨率下和不同采样率下R矩阵乘法运算时间.图像数值分辨率为128×128,在不同的k空间采样率下,R矩阵乘法8次运算时间的均值和标准差如表 3所示.另一方面,在不同的数值分辨率下,全采样的R矩阵的乘法8次运算时间的均值和标准差如表 4所示.两表都表明了使用GPU能够大幅度减小R矩阵乘法运算的时间,使得算法能够应用于实际的应用场景中.对于分辨率为128×128,50%欠采样数据量的磁共振图像仿真实验,用GPU实现乘法的速度比CPU实现的速度快100倍左右,通过使用GPU和MATLAB混合编程使得STT-CS重建算法运行时间减小到16 s左右,与NUFFT-CS算法的10 s运行时间相近.此外,拥有更多核心和更高主频的GPU能够进一步加速运算时间,以解决更高数字分辨率的图像重建问题.以当前比较先进的GPU(NVIDIA,GTX TITAN X)为例,核心已经达到3 072个,因此R矩阵计算时间能够进一步减小.
| 采样率% | CPU运算时间/ms | GPU运算时间/ms |
| 12.5 | 556±104 | 2±6 |
| 25 | 1067±104 | 12±7 |
| 50 | 2202±221 | 21±8 |
| 100 | 4294±295 | 37±8 |
| 数值分辨率 | CPU运算时间/ms | GPU运算时间/ms |
| 64 | 211±12 | 2±6 |
| 128 | 4725±337 | 39±8 |
| 256 | 43643±1665 | 575±15 |
螺旋采样在功能性成像、并行成像和动态成像中发挥着越来越重要的作用.本文介绍了非网格化的STT-CS重建算法,并使用GPU并行编程加速.
STT-CS重建算法通过构造空间变换矩阵,直接将数据作为最优化模型的数据保真项,避免了传统算法中网格化的过程和误差.压缩感知和欠采样的结合使得螺旋采样所需的点数更少且重建效果良好.虽然该时间空间变换矩阵的复杂度大,但是GPU并行计算的方式加速了算法运行,使得算法具有较强的应用价值.
螺旋采样已经发展到多轨迹的并行采样.通过拼合多轨迹的数据,可以将STT-CS重建算法应用到多轨迹的螺旋采样数据.此外,不均匀场会造成磁共振图像的扭曲.如何矫正不均匀场下的螺旋采样的磁共振图像的扭曲是一个具有实际意义的课题.
| [1] | Yang Bao-lian(杨保联) . Future of ultra high field MRI in basic research and clinical applications(超高场磁共振人体成像应用研究和医学前景)[J]. Chinese J Magn Reson(波谱学杂志) , 2015, 32 (4) : 707-714 |
| [2] | Haacke E M, Brown R W, Thompson M R et al . Magnetic Resonance Imaging:Physical Principles and Sequence Design[M]. New York: Wiley-Liss, 1999 . |
| [3] | Sachs T S, Meyer C H, Hu B S et al . Real-time motion detection in spiral MRI using navigators[J]. Magn Reson Med , 1994, 32 (5) : 639-645 DOI:10.1002/(ISSN)1522-2594 |
| [4] | Meyer C H, Hu B S, Nishimura D G et al . Fast spiral coronary artery imaging[J]. Magn Reson Med , 1992, 28 (2) : 202-213 DOI:10.1002/(ISSN)1522-2594 |
| [5] | Tolouee A, Alirezaie J, Babyn P . Compressed sensing reconstruction of cardiac cine MRI using golden angle spiral trajectories[J]. J Magn Reson Imaging , 2015, 260 : 10-19 DOI:10.1016/j.jmr.2015.09.003 |
| [6] | O'Sullivan J D . A fast sinc function gridding algorithm for Fourier inversion in computer tomography[J]. IEEE T Med Imaging , 1985, 4 (4) : 200-207 DOI:10.1109/TMI.1985.4307723 |
| [7] | Jackson J, Meyer C H, Nishimura D G et al . Selection of a convolution function for Fourier inversion using gridding[J]. IEEE T Med Imaging , 1991, 10 (3) : 473-478 DOI:10.1109/42.97598 |
| [8] | Sha L, Guo H, Song A W . An improved gridding method for spiral MRI using nonuniform fast Fourier transform[J]. J Magn Reson Imaging , 2003, 162 (2) : 250-258 DOI:10.1016/S1090-7807(03)00107-1 |
| [9] | Fessler J A . On NUFFT-based gridding for non-Cartesian MRI[J]. J Magn Reson Imaging , 2007, 188 (2) : 191-195 DOI:10.1016/j.jmr.2007.06.012 |
| [10] | Candès E J, Wakin M B . An introduction to compressive sampling[J]. IEEE Signal Proc Mag , 2008, 25 (2) : 21-30 DOI:10.1109/MSP.2007.914731 |
| [11] | Donoho D L . Compressed sensing[J]. IEEE T Inform Theory , 2006, 52 (4) : 1289-1306 DOI:10.1109/TIT.2006.871582 |
| [12] | Li Zhi-min(李智敏), Xie Hai-bin(谢海滨), Zhou Min-xiong(周敏雄) et al . Spike noise removal for magnetic resonance imaging based on sparse reconstruction(基于稀疏重建的磁共振图像尖峰噪声消除方法)[J]. Chinese J Magn Reson(波谱学杂志) , 2015, 32 (01) : 41-50 |
| [13] | Lustig M, Donoho D, Pauly J M . Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magn Reson in Med , 2007, 58 (6) : 1182-1195 DOI:10.1002/(ISSN)1522-2594 |
| [14] | Owens J D, Houston M, Luebke D et al . GPU computing[J]. P IEEE , 2008, 96 (5) : 879-899 DOI:10.1109/JPROC.2008.917757 |
| [15] | Sanders J, Kandrot E . CUDA by Example:An Introduction to General-purpose GPU Programming[M]. Boston: Addison-Wesley, 2010 . |
| [16] | Yang J, Zhang Y, Yin W . A fast alternating direction method for TVL1-L2 signal reconstruction from partial fourier data[J]. IEEE J STSP , 2010, 4 (2) : 288-297 |
| [17] | Zhan Z, Cai J, Guo D et al . Fast multi-class dictionaries learning with geometrical directions in MRI reconstruction[J]. IEEE T Bio-Med Eng , 1109 DOI:10.1109/TBME.2015.2503756 |

本作品采用知识共享署名 4.0 国际许可协议进行许可。
 2016, Vol. 33
2016, Vol. 33



