引言

幅值和相位是磁共振图像的基本组成部分.以往的磁共振图像应用更为关心幅值图，但是近年来的相关研究开始越来越重视相位图的作用.基于相位图的各种成像技术，例如相位对比度流速测量（Phase Contrast Velocity Measurement）技术^{[1, 2]}、质子自旋频率温度测量（Proton Resonant Frequency Temperature Measurement）技术^{[3, 4]}、定量磁化率成像（Quantitative Susceptibility Mapping，QSM）技术^[5-11]等，发展迅猛并得以广泛地应用.

多通道相控阵线圈广泛应用于磁共振信号的采集.相比于体线圈，多通道相控阵线圈可以提供更高的信噪比（Signal-to-Noise Ratio，SNR）^[12]，同时可以支持基于灵敏度编码（SENSitivity Encoding, SENSE）^[13]和自校准并行采集（GeneRolized Autocalibrating Partially Parallel Acquisition, GRAPPA）^[14]的并行成像技术.

多通道幅值图像的合并比较简单，使用传统的平方和（Sum Of Squares，SOS）方式就可以得到较好的合并结果^[15].但是多通道复数图像的合并较为复杂，原因在于每个相控阵线圈摆放位置以及负载状态等的不同，每个线圈重建出来的图像都会叠加出一个独有的相位偏移^[16].如果这些相位偏移没有被移除，就会影响到合并后的相位图像.例如在传统的加权平均（Weighted Mean，WM）方法^[16]中，使用每个通道幅值图作为权重系数加权对应的复数图，最后取平均.这种方法没有去除相位偏移，可能引起信号抵消，导致合并后的幅值图和相位图信噪比较低.传统的低场仪器扫描时可能会使用体线圈进行参考扫描，得到各个线圈的复数灵敏度信息，作为加权系数进行重建^[17]. 但是对于一些没有体线圈的高场磁共振设备来说，这一扫描无法实现.对于多回波的采集形式，厄米特乘积（Hermitian-Product，HP）方式^[16]可以有效去除各个通道的相位偏移，但是这种方法不适用于单个回波的采集形式.相比于以上提到的这些方法，Walsh等人^[15]在2000年提出的自适应重建（Adaptive Reconstruction，AR）算法，同时适用于单回波以及多回波的情形，并可以有效地提高重建后的幅值图和相位图的信噪比.但是AR算法更偏向于优化幅值图像，对于相位图像，在各个通道相位偏移较大、单个通道相位信噪比较低的情况下，可能会导致尖端伪影（Cusp Artifact）的出现.

本文改进了AR算法.首先对于多通道数据，估算并移除了每个通道引入的相位偏移，然后对各个通道的相位数据进行质量评估并依据质量高低进行通道重排，最后进行自适应重建，得到合并后的相位图.实验结果表明，本文提出的方法可以有效提高AR算法的稳定性，同时保持合并后的相位图的高信噪比.

1 理论 1.1 信号模型

磁共振成像实验中，使用多通道线圈采集得到的复数图像可以表示为：

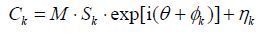
(1)

其中，k表示线圈通道编号（k = 1, 2, …, N），C_k表示第k个线圈采集到的复数图像，M和θ表示物体实际产生的磁共振信号幅值和相位，S_k和${{\phi }_{k}}$分别表示由第k个接收线圈灵敏度引入的幅值和相位调制，${{\eta }_{k}}$表示噪声项.由于线圈摆放位置的不同，各线圈之间的灵敏度差异很大.在多通道合并过程中，${{\phi }_{k}}$的巨大差异以及${{\phi }_{k}}$中存在的奇异点都有可能影响重建相位图像的正确性.因此应当在通道合并之前被去除.

1.2 传统AR算法^[15]

AR算法需要估算一个N×1的复数滤波向量m = [m₁, m₂, …, m_N]^T，用于合并多个通道^[15]，合并后的复数图像I用(2) 式表示：

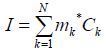
(2)

用s和n表示各通道信号和噪声过程构成的随机向量，${{\mathbf{m}}^{\text{H}}}\mathbf{s}$和${{\mathbf{m}}^{\text{H}}}\mathbf{n}$表示通道合并后的信号和噪声随机过程，用(3) 式最大化合并后的幅值图的信噪比^[15]：

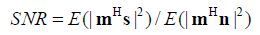
(3)

求解上式得到的最优化滤波向量m是矩阵$\mathbf{P}={{\mathbf{R}}_{\text{n}}}^{-1}{{\mathbf{R}}_{\text{s}}}$最大特征值对应的单位化特征向量^[18].其中，R_n及R_s表示不同通道之间噪声以及信号的相关矩阵.

m的幅值需要保证对各个通道幅值图像加权后，合并得到的幅值图有最大的信噪比.m的相位需要保证经过复数相乘得到的各个${{m}_{k}}^{*}{{C}_{k}}$的相位一致，从而保证在(2) 式求和过程中不会发生信号抵消和信噪比降低.

值得注意的是，若向量m是矩阵P的单位化特征向量，则向量$\mathbf{m}\cdot \exp (\text{i}\cdot \xi )$必然也是P的单位化特征向量，其中x表示任意的相位角度.即在(3) 式中，若存在向量m使得合并后幅值图的信噪比达到最大值，则必然存在无数多个向量，同样使得该信噪比达到最大值.事实上，m的相位只要求保证(2) 式中每个求和项相位一致即可，并不要求是某个具体值.因此使用(2) 式滤波后得到的合并图像I的相位是不确定的.在实际应用中，经常令m的第一个元素为正实数，这样就保证了m的唯一性. 该操作的缺点是会使得合并后图像相位与第一个通道相位接近，如果第一个通道相位信噪比较低或奇异点较多，就会影响到合并后的相位结果.

1.3 改进型AR算法

如引言部分所述，传统AR算法在通道间相位偏移较大、偏移相位存在伪影以及单个通道相位图信噪比较低的情况下，重建出来的相位图可能会出现尖端伪影，为了解决这个问题，本文提出了改进型AR（improved AR，iAR）算法.该算法主要分为以下三个步骤.

1.3.1 估算并移除相位偏移φk

（1）使用多个回波中的一个，将其对应多通道相位图像进行高通滤波，由于各个通道的相位偏移${{\phi }_{k}}$为低频成分，因此会在滤波过程中被滤除.

（2）将滤波后的结果使用WM方法结合到一起，得到初步的单回波相位图$\hat{\theta }$.

（3）从原始单回波相位图中逐通道移除，得到各通道相位偏移的估计值${{\hat{\phi }}_{k}}$.

（4）将${{\hat{\phi }}_{k}}$进行低通滤波，消除噪声，得到相位偏移${{\phi }_{k}}$，并将其从原始多回波数据中移除.

1.3.2 数据质量评估及通道重排

从原始多回波数据中移除相位偏移${{\phi }_{k}}$后，各个通道的相位图应当比较接近.但是由于某些通道幅值及相位信噪比较低，信号湮没于噪声之中，该通道处相位会与其他通道对应点相位（以及真实相位）有较大差异.由1.2节可知，如果第一个通道相位信噪比较低、误差较大，必然会影响到自适应重建的相位.因此，有必要对所有通道数据进行评估，选取质量最高的通道作为第一个通道，进行自适应重建.具体分析及操作过程如下：

磁共振图像中的噪声可以认为是加性高斯白噪声^[18].Vegh等人^[18]的研究表明：在复数图像幅值信噪比较低的情况下，相位分布近似呈均匀分布；在复数图像幅值SNR≥3时，相位分布近似呈高斯分布.因此可以认为，正常信噪比情况下，各个通道之间的相位符合高斯分布.如果某个通道相位偏离均值较大，可以认为该通道对应相位为奇异相位.

在移除相位偏移后，计算各通道相位的均值（${{\bar{S}}_{0}}$），逐点对各通道相位解卷绕，使其落到${{\bar{S}}_{0}}\pm \text{ }\!\!\pi\!\!\text{ }$以内.使用解卷绕后的相位，再次计算各个通道之间相位的均值（$\bar{S}$）及标准差（Standard Deviation, SD）.标记$\bar{S}\pm 3SD$范围以外的相位为奇异相位.逐点计算得到每个通道奇异相位分布图，选取奇异相位点总数最少的通道作为第一个通道，进行后续自适应重建.

1.3.3 自适应重建

对1.3.2节中重排后的多通道数据，使用传统AR算法进行通道合并，得到最终合并后的复数图像.

2 材料与方法 2.1 实验设计

实验包括仿体实验及在体实验两部分，仿体成像实验对象为圆柱体水模，在体成像实验部位为志愿者脑部区域.所有的扫描实验均在Philips 3.0 T Achieva TX MRI设备（Philips Healthcare, Best, The Netherlands）上完成.采用32通道头线圈作为接收线圈. 仿体实验参数如下：使用2D多回波梯度回波采集序列，共采集4个回波，TR/TE₁/DTE = 447 ms/3.6 ms/5.0 ms，翻转角（FA）= 18˚，采集视野（FOV）= 230×230 mm²，采集矩阵=256×256，层厚=2 mm，共采集20层，采集时间为116 s.在体实验1参数如下：使用2D多回波梯度回波采集序列，共采集4个回波，TR/TE₁/DTE = 892 ms/3.6 ms/5.0 ms，翻转角（FA）= 18˚，采集视野（FOV）= 230×230 mm²，采集矩阵=256×256，层厚=2 mm，共采集40层，采集时间为232 s.在体实验2参数如下：使用3D多回波梯度回波采集序列，共采集4个回波，TR/TE₁/DTE = 24 ms/5.0 ms/5.0 ms，翻转角（FA）= 17˚，采集视野（FOV）= 230×230×80 mm³，采集矩阵=256×256×40，采集时间为237 s.所有实验都没有采用SENSE^[13]或者GRAPPA^[14]加速.在体实验均得到了当地伦理委员会审核通过.

2.2 数据处理与分析 2.2.1 仿体实验数据处理与分析

对于仿体数据，逐层进行以下处理.首先使用第一个回波图像按照1.3.1节中方法估算每个通道相位偏移，并将其从4个回波中移除.然后对4个回波同时进行分析.

使用1.3.2节中的数据质量评估方法，选取出相位奇异点最少的通道，将其重排至第一个通道，进行后续自适应重建.

为分析本文提出的iAR算法的表现，对于采集得到的数据，本文还会另外采用以下三种方式重建：（1）将原始多通道数据直接使用WM算法重建；（2）将原始多通道数据直接使用AR算法重建；（3）将移除相位偏移后的数据使用AR算法重建（AR with Phase Offsets Removed，AR-POR）.需要注意的是，AR-POR算法比iAR算法少了通道重排操作.

对于4种重建方式得到的重建后相位图像，首先观察是否有尖端伪影存在，然后选择感兴趣区域（Region Of Interest，ROI），分析ROI内相位分布的，用以评价使用4种算法重建的相位图像的信噪比.

2.2.2 在体实验1数据处理与分析

对于在体实验1采集的2D数据，使用与2.2.1节中相同的4种重建算法进行通道合并.对通道合并后的相位图，使用质量引导的2D相位解卷绕算法^[19]解卷绕，再对解卷绕后的相位图分别进行高通滤波，得到高频相位图，用于后续评估.

2.2.3 在体实验2数据处理与分析

对于在体实验2采集的3D数据，使用同上4种重建算法进行通道合并.为了评价4种算法得到相位图的正确性，对合并后的相位图进一步使用Li等人^{[9, 20, 21]}的方法处理得到磁化率分布图.具体步骤为：使用基于Laplacian算子的方法进行相位解卷绕^[9]，使用HARPERELLA（HARmonic PhasE REmovaL using the LAplacian operator）算法移除背景相位^[21]，再使用最小二乘QR分解（Least Squares QR-factorization, LSQR）算法求解磁敏感系数^[9]，得到磁化率分布图，用于后续评估.

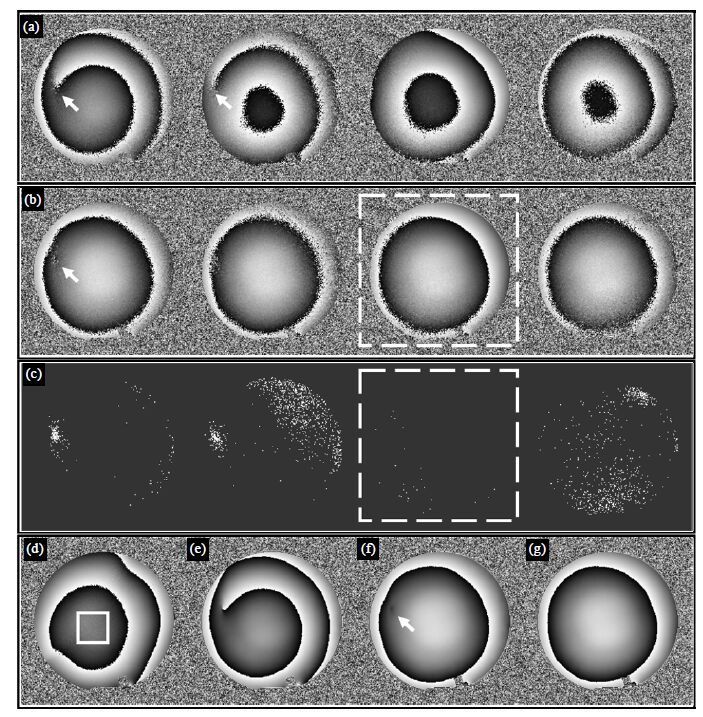
3 结果与讨论 3.1 仿体实验结果

图 1为仿体实验结果，此处仅显示第三个回波第1、8、16、24个通道的处理过程.原始多通道相位之间差异很大，在某些通道中，还会有相位奇异点存在[图 1(a)箭头所示]，在估算并移除各个通道相位偏移后，各通道之间相位变得非常接近[图 1(b)].对该多通道相位数据进行质量评估，可以得到各通道奇异相位点分布图[图 1(c)].基于该奇异相位分布图，选取奇异相位点最少的通道[图 1(b)和(c)虚线方框]，将其重排至第一通道，并使用AR算法重建后得到的合并后相位图如图 1(g)所示.直接将原始多通道数据使用WM算法及AR算法重建得到的相位图如图 1(d)和图 1(e)所示，去除相位偏移后的多通道数据使用AR算法重建得到的相位图如图 1(f)所示.

分别选取合并后相位图像中间30×30区域[图 1(d)方框所示]为感兴趣区域，计算得到各重建算法的相位标准差分别为WM/AR/AR-POR/iAR = 0.21/0.14/0.13/0.14，可以看出相对于WM算法，AR算法可以有效提高重建后的相位图的信噪比.

传统AR算法重建的相位图像[图 1(e)]与原始数据第一通道相位图像[图 1(a)]接近，这与2.1节的分析相符合.AR算法重建图像中的尖端伪影在图 1(f)与图 1(g)中被消除，显示了移除各通道相位偏移的重要性.AR-POR算法重建得到的结果[图 1(f)]中虽然没有了尖端伪影，但是仍然有相位不均匀点存在[图 1(f)箭头]，这是由图 1(b)中箭头所示处的错误相位引起的，这一相位不均匀点在图 1(g)中被消除，显示了进行数据评估及通道重排的重要性.

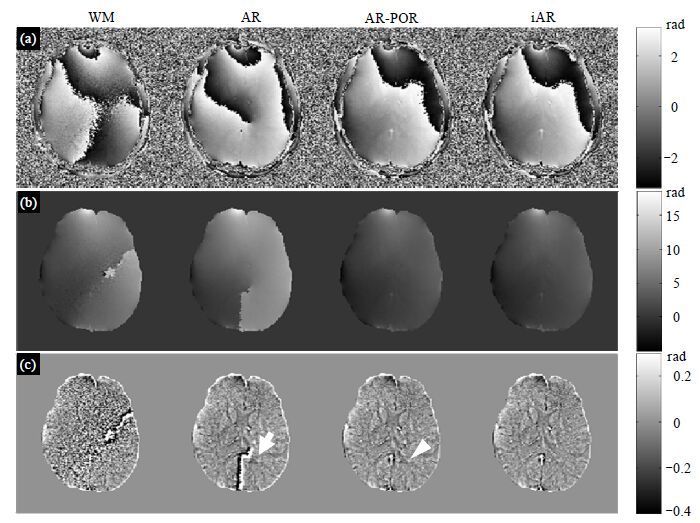
3.2 在体实验1结果

图 2为在体实验1结果.对使用4种不同算法重建出来相位图像[图 2(a)]进行2D相位解卷绕后得到图 2(b)，再高通滤波后得图 2(c)，可以看出，WM算法重建结果信噪比低，并且存在尖端伪影.传统AR算法重建结果信噪比较高，但是其中存在的尖端伪影无法在相位解卷绕过程中消除，最终会出现在高通滤波后的相位图像上[图 2(c)箭头].而移除相位偏移的两种重建算法——AR-POR和iAR均不存在这个问题.AR-POR算法和iAR算法重建出的相位和解卷绕后的相位都比较接近，但是在高通滤波后的AR-POR算法重建相位图中，仍然可以看到一小片不均匀区域[图 2(c)三角].而在经过数据质量评估及通道重排后的iAR算法中，这种不均匀性被消除.

3.3 在体实验2结果

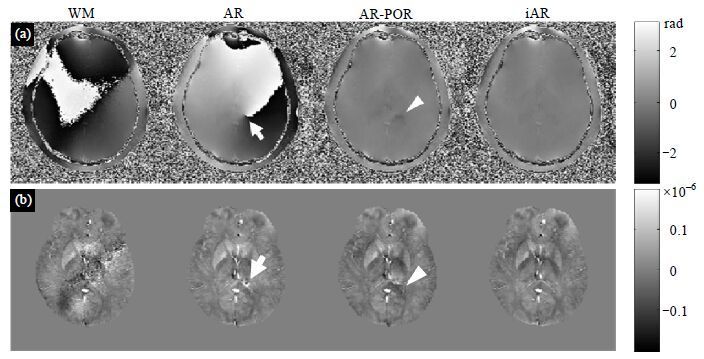
图 3为在体实验2结果.对使用4种不同算法重建出来相位图像[图 3(a)]进行磁化率反演计算，得到的磁化率分布图如图 3(b)所示.使用WM算法重建，最后得到的磁化率分布图信噪比较低，无法使用.使用传统AR算法重建，最后得到的磁化率分布图信噪比较高，但是由于合并后相位图像存在尖端伪影[图 3(a)箭头]，导致磁化率分布图中出现白点[图 3(b)箭头]，这个白点可能会被错误诊断为微出血^[22].使用AR-POR算法重建出来相位图中没有尖端伪影，计算得到的磁化率分布图中也不存在白点，但是重建出的相位图及磁化率分布图中均有小片模糊区域[图 3(a)及(b)中三角所示].该区域在使用iAR算法的磁化率分布图中被消除.

3.4 讨论

传统AR算法中，如果通道相位偏移相差较大，偏移相位存在伪影，单个通道相位图信噪比较低等，都可能导致重建出的相位图像出现尖端伪影，较为模糊.针对这些问题，本文提出了iAR算法.实验结果表明，该算法在保持AR算法高信噪比的同时，可以有效消除由于相位偏移及某些通道相位信噪比较低等引入的伪影，提升算法稳定性.

相位图是磁共振图像的重要组成部分，基于相位图的磁共振成像技术需要没有伪影、高信噪比的相位图.通过使用本文提出的方法，移除相位偏移，并进行数据质量评估及通道重排后，可以得到更加稳定及精确的相位结果，从而可以为科研及临床应用提供更加准确的信息.

在进行通道质量评估过程中，需要选取奇异相位最少的通道，作为第一个通道进行后续重建，从而保证重建出相位图像的正确性.在极端情况下，所有通道奇异相位点都很多，此时可以使用虚拟参考线圈（Virtual Reference Coil）^[22]的方法，将所有去除相位偏移后的数据使用加权平均的方式结合到一起，构成参考线圈，当做第一个通道. 由于这个通道数据是其他所有通道的线性组合，因此不会影响到后面自适应重建过程.

本文在传统AR算法重建之前增加了两个步骤，因此处理时间会有所增长.自适应重建本身比较耗时，相对来说，本文提出的iAR算法增加的时间并不是很多：对于32通道256×256分辨率的单层图像，传统AR算法重建耗时约52.9 s，而iAR算法重建耗时约66.1 s.如果想要进一步加速，可以在进行各通道数据质量评估时，尝试将原始数据适当降采后再计算各通道相位偏移.

4 结论

本文提出了iAR算法，估算并移除了多通道相位偏移，结合数据质量评估、通道重排等操作，改进了传统AR算法的稳定性.该技术可以有效地应用于多通道相位图像的重建.