文章信息
- 王鹏飞, 王晨, 何胜国, 梅刚华
- WANG Peng-fei, WANG Chen, HE Sheng-guo, MEI Gang-hua
- 一种用于高精度小型化铷频标的开槽管微波腔
- A Slotted-Tube Microwave Cavity for High Performance Miniaturized Rubidium Frequency Standards
- 波谱学杂志, 2016, 33(3): 452-457
- Chinese Journal of Magnetic Resonance, 2016, 33(3): 452-457
- http://dx.doi.org/10.11938/cjmr20160310
-
文章历史
收稿日期: 2015-11-11
收修改稿日期: 2016-07-15


DOI:10.11938/cjmr20160310
2. 中国科学院原子频标重点实验室, 武汉 430071;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Atomic Frequency Standards, Chinese Academy of Sciences, Wuhan 430071, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
铷原子频标在高精度和小型化两方面的研究都取得了长足进展.用于卫星导航的高精度铷频标短期频率稳定度已达到优于1×10-12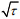
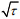
得到体积小、共振模式好的微波腔是研制兼具小型化和高精度特性铷原子频标的关键.共振模式决定微波腔中微波场的分布,如果微波场磁力线沿C场方向均匀、密集分布,就可以激励出强的原子跃迁信号,保证铷频标的频率稳定度.减小微波腔体积主要有两种途径:一种是在标准腔(如TE111腔)中填充介质[3],但是这样得到的微波腔小型化程度依然不高,共振模式也不理想;另一种是采用非标准腔,如磁控管式微波腔[4]和本实验室研制的开槽管微波腔[5],效果更好一些.康松柏等人[6]报道过一款体积为18 mL的开槽管微波腔,该微波腔可以满足研制短期频率稳定度为的3.8×10-12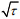
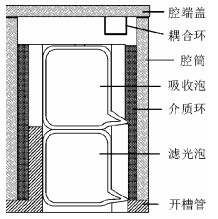
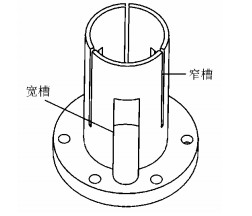
在铷原子频标中,微波腔是腔泡系统的重要部件.开槽管微波腔是一种新型微波腔,由腔筒、腔端盖、介质环和开槽管组成(如图 1所示).开槽管是微波腔的核心,主体结构是一个上端开有若干个等间距窄槽的金属圆筒.开槽管外安装一个由电介质材料制作的介质环,内部安装铷吸收泡和滤光泡,底部通过法兰与腔筒连接.开槽管腔的工作原理与环隙腔[7]类似,都是通过由极片和窄槽组成的感容结构与外部通入的微波信号的共振,激发所需的驻波场(如图 2所示).开槽管腔内微波能量主要集中在开槽处,即开槽管的上部,没有开槽的下部能量弱.利用这种特性,将吸收泡放置在开槽管内的上部,滤光泡放置在开槽管内的下部,就可以得到一个集成度很高的分离滤光腔泡系统.腔泡系统采用分离滤光设计有利于提高原子鉴频信号的信噪比,从而使铷频标具备高的频率稳定度.
|
| 图 1 开槽管微波腔结构 Fig. 1 Structure of slotted-tube cavity |
|
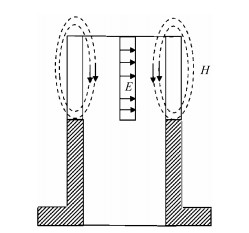
| 图 2 开槽管微波场激发原理示意图 Fig. 2 Field configurations of slotted-tube |
对于铷原子频标,要求微波腔的谐振频率为钟跃迁频率6 834 MHz.开槽管腔的微波谐振频率与槽的数目、宽度、深度,极片厚度,开槽管内径,介质环长度,腔筒长度和内径等参数相关[8].减小腔体积的关键是减小腔筒的长度和内径,但是这两个尺寸减小后会使得腔频升高.另一方面,开槽数目对微波腔频率影响也很显著:槽数越少,谐振频率越低,故可通过减少槽数降低腔频.文献[6]使用的是8个槽,高频结构仿真软件HFSS仿真结果显示,此时很难将微波腔体积进一步减小.为了在保持腔频不变的情况下进一步减小腔的体积,我们采用了如图 3所示的开槽管设计方案,将槽数减至3个.通常使用的吸收泡侧壁有一泡尾,为方便吸收泡的安装,需要在开槽管下端开一个宽槽.仿真计算显示,如果仅开一个宽槽,会破坏微波场的对称性.为了保证微波场的对称性,我们在开槽管的下部开了3个均匀分布的宽槽.根据仿真参数设计加工得到的微波腔实物示于图 4,腔的外形轮廓体积仅为11 mL,比文献[6]减小了约1/3.
|
| 图 3 开槽管结构.上部开有3个窄槽,下部开有3个宽槽 Fig. 3 Structure of the slotted-tube. The top has 3 slim slots and the bottom has 3 broad slots |

|
| 图 4 开槽管微波腔实物.腔筒外上部的线圈为加热线圈,下部为C场线圈 Fig. 4 Assembled prototype of slotted-tube cavity. The coil on the upside is used as heat coil and the other coil is C field coil |
对于铷原子频标,在微波腔内铷吸收泡所在的原子共振区,只有与C场平行的微波场磁分量才能激励钟跃迁.共振区内微波场磁分量与C场方向(即腔轴方向)的平行度越高,原子跃迁信号就越强,铷频标的频率稳定度也会越高.所以,微波场的方向因子是微波腔的关键特性,它定义为共振区中微波场轴向分量场(Hz)强度与其总强度之比[9]:
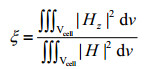 (1)
(1)
其中,Vcell为吸收泡所占区域,Hz表示微波场轴向分量.
用HFSS软件仿真得到的开槽管腔中微波场磁力线分布示于图 5.磁力线颜色由蓝变红表示微波能量由弱变强.由图 5可看出,开槽管内上部共振区内微波能量最强,磁力线的方向基本上与腔轴平行.

|
| 图 5 仿真得到的微波腔纵截面磁力线分布 Fig. 5 Simulated magnetic field distributed in the cavity |
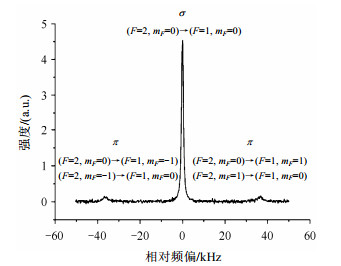
方向因子可以用软件仿真得到,也可以从实验上测量.文献[10]给出了一种通过测量87Rb原子基态Zeeman子能级跃迁谱线强度确定微波方向因子的方法.用该方法测量了开槽管腔腔泡系统中铷原子Zeeman跃迁谱,结果示于图 6.基于实测结果,开槽管腔的微波方向因子可用下式确定:
|
| 图 6 87Rb原子基态Zeeman跃迁谱.其中σ表示微波场轴向分量激发的跃迁,π表示径向分量激发的跃迁,F、mF表示相应跃迁能级 Fig. 6 Zeeman spectrum of 87Rb ground transitions. Transition stimulated by axial component of magnetic field is σ and that by radial component of magnetic field is π. (F, mF) is the corresponding transition state |
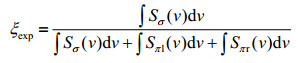 (2)
(2)
其中为图 6中微波场轴向分量激发的跃迁信号(σ)的强度,和分别为左右两个微波场径向分量激发的跃迁信号(π)的强度.
实验测量得到的方向因子为0.83,相应的软件仿真计算结果为0.89,两者相差不大.表明共振区内,微波磁场与C场平行度较高,有利于激发较强的原子共振跃迁信号,进而实现较高的频率稳定度,所以本文设计的微波腔可用于小型化高精度铷频标.
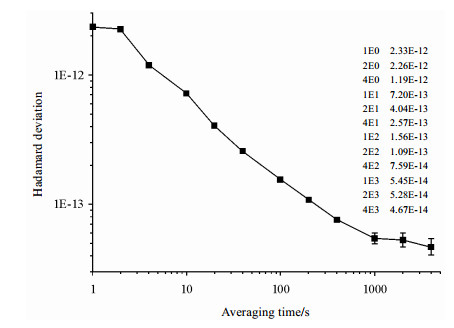
3 铷频标频率稳定度测试结果利用这种开槽管腔,设计了小型化铷原子频标物理系统,形成了小型化铷原子频标桌面系统.以氢原子钟为参考源,用瑞士SpectraTime公司的Picotime频率稳定度测试仪测量了系统的频率稳定度,其采样间隔为1 s,结果示于图 7.由图 7可见,采样时间为1s、10s和100s的频率稳定度分别为2.3×10-12、7.2×10-13和1.6×10-13.该款频稳测试仪的1s稳和10s稳测量能力受限,而100s稳的测量结果是可信的.据此分析,系统的短期频率稳定度应该优于2×10-12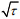
|
| 图 7 铷原子频标频率稳定度测试曲线 Fig. 7 Measured stability of the rubidium atomic frequency standards (RAFS) |
本文设计了一种用于铷原子频标的开槽管微波腔.通过减少开槽数量,得到了迄今为止体积最小的开槽管微波腔,体积仅为11 mL.仿真计算得腔内微波场的方向因子为0.89,通过测量87Rb原子基态Zeeman子能级跃迁谱线的强度,得到腔内微波场方向因子为0.83,和仿真结果大致相当.基于该微波腔制作了一台铷原子频标桌面整机,短期频率稳定度测量结果优于2×10-12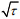
| [1] | Vannicla F, Beard R, White J, et al. GPS block IIF rubidium frequency standard life test[C]. Santa Ana Pueblo, USA: 41st Annual Precise Time and Time Interval (PTTI) Meeting, 2009. |
| [2] | LPFRS High-Performance Rubidium Oscillator[EB/OL]. www.Spectratime.com |
| [3] | 王艳, 余钫, 朱熙文, 等. 汽室型铷原子频标中微波腔的小型化[J]. 宇航计测技术 , 2007, 27 (5) : 41-44 Wang Yan, Yu Fang, Zhu Xi-wen, et al. A downsized microwave cavity for the rubidium vapor cell frequency standard[J]. Journal of Astronautic Metrology and Measurement , 2007, 27 (5) : 41-44 |
| [4] | Schweda H, Busca G, Rochat P. Atomic frequency standard: European patent, 0561261[P]. 1997. |
| [5] | Xia B H, Zhong D, An S F, et al. Characteristics of a novel kind of miniature cell cavity for rubidium frequency standards[J]. IEEE T Instrum Meas , 2006, 55 (3) : 1000-1005 DOI:10.1109/TIM.2006.873786 |
| [6] | 康松柏, 赵峰, 王芳, 等. 铷原子频标物理系统小型化设计[J]. 计量学报 , 2012, 33 (1) : 72-76 Kang Song-bai, Zhao Feng, Wang Fang, et al. Design of miniaturized physics package for rubidium atomic frequency standards[J]. Acta Metrologica Sinica , 2012, 33 (1) : 72-76 |
| [7] | Mehdizadeh M, Ishii T, Hyde J, et al. Loop-gap resonantor: A lump mode microwave resonant structure[J]. IEEE T Microw Theory , 1983, 31 (12) : 1113-1118 |
| [8] | 夏白桦.铷原子频标物理系统研制与参数优化[D].武汉:中国科学院武汉物理与数学研究所, 2004. Xia Bai-hua. Physics Package and Parameter Optimization for Vapor Cell Rubidium Atomic Frequency Standards[D]. Wuhan: Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, 2004. |
| [9] | Stefanucci C, Bandi T, Merli F, et al. Compact microwave cavity for high performance rubidium frequency standards[J]. Rev Sci Instrum , 2012, 83 (10) : 104706 DOI:10.1063/1.4759023 |
| [10] | 许风.基于开槽管微波腔的高信噪比铷钟物理系统[J].计量学报, 待出版 Xu Feng. Acta Metrologica Sinica, in press. |
 2016, Vol. 33
2016, Vol. 33



