文章信息
- 高芒, 谢海滨, 李智敏, 张成秀, 奚伟, 姜小平, 杨光
- GAO Mang, XIE Hai-bin, LI Zhi-min, ZHANG Cheng-xiu, XI Wei, JIANG Xiao-ping, YANG Guang
- 压缩感知同步扫描重建及其采样方案的研究
- A Synchronized Compressed Sensing Scan-Reconstruction Scheme in Magnetic Resonance Imaging
- 波谱学杂志, 2016, 33(2): 257-268
- Chinese Journal of Magnetic Resonance, 2016, 33(2): 257-268
- http://dx.doi.org/10.11938/cjmr20160208
-
文章历史
收稿日期: 2015-05-19
修订日期: 2016-04-09


DOI:10.11938/cjmr20160208
2. 上海卡勒幅磁共振技术有限公司, 上海 201614
2. Shanghai COLORFUL Magnetic Resonance Technology Corporation Limited, Shanghai 201614, China
软组织的磁共振成像(magnetic resonance imaging,MRI)对比度高、信息丰富、对人体没有伤害,在临床上得到了广泛应用.MRI的主要弱点之一就是扫描速度慢,这不仅影响了设备的利用率,增加了MRI检查的成本,也增加了病人在扫描过程中的不适感,更容易由于病人运动而产生伪影、影响图像质量[1].压缩感知(compressed sensing,CS)作为一种新的采样-重建技术,可以用远低于奈奎斯特采样定理要求的频率来采集数据,通过非线性重建比较准确地还原出原始信号[2][3].原始信号被还原的准确性受到稀疏变换、欠采样模式以及重建算法等方面的影响[5].将CS方法应用于MRI,可以减少k空间的采样点数,缩短MRI扫描时间,减少MRI检查的成本,因而在临床上具有重要的实践意义.
近几年来,CS-MRI方法已成为医学影像领域的热点之一[6].CS-MRI大大提高了MRI的时间分辨率,在动态MRI领域中获得了成功地应用.如利用CS的动态MRI,可以对心脏收缩运动进行观察[7].
然而,时至今日,在常规临床检查中最常用的静态MRI扫描中,CS还没有获得明确的应用.造成这种现象的主要原因是:(1)通过CS方法得到的重建图像与全采样k空间数据经傅里叶变换后的完美重建图之间仍有一定的差距,在图像质量上虽然可以满足动态成像的要求,但还难以达到静态图像的要求;(2)CS重建算法是一个迭代运算的非线性最优化的过程,耗费时间较长.在动态成像中,常常是先进行数据采集,然后离线进行图像重建.这种做法对于常规临床检查并不适用.
CS要在常规临床检查中获得广泛应用,首先必须解决上面两个问题.我们认为,同步扫描重建(以下简称同步重建)可以为上面两个问题提供很好的解决方案.同步重建,就是边扫描边利用已采样数据进行图像重建,将重建的迭代优化过程与扫描的循环过程融合起来.这样,在扫描初期就能观察重建图像.随着扫描过程的进行,采样数据越来越多、重建图像质量越来越好,直到图像质量达到要求或者整个扫描重建过程达到预设的终止条件.这样既可以及时发现病人运动等影响图像质量的问题,也可以在CS重建效果不满意时继续采样,还原为全采集模式.利用扫描时间来进行图像重建,也有助于克服重建速度慢、扫描总时间长等问题.同步重建的具体过程如图 1所示.
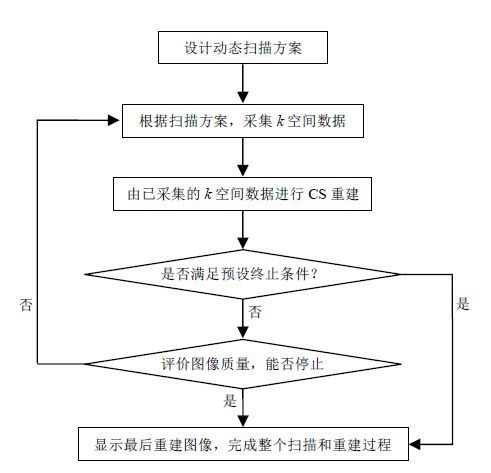
|
| 图1 同步扫描-重建过程的流程图 Fig.1 Flowchart of synchronized scanning-reconstruction |
CS理论要求使用满足约束等距性(restricted isometry property,RIP)[9]的采样矩阵采集数据,通过非线性优化算法(如共轭梯度法[6]、分裂布雷格曼算法[10]等)来恢复信号.CS-MRI常用的采样模式是在采样率固定的情况下,在相位编码维上采用基于概率密度函数(probabitity density function,PDF)的变密度伪随机采样[6].而同步重建带来的一个新问题是,根据重建效果的不同,整个扫描重建的过程可能会在不同的采样率下终止,因此不能完全沿用传统的固定采样率的CS随机采样模式,需要设计出一种适用于同步重建过程的采样模式,从而实现在此过程中始终能得到质量尽可能好的重建图像.
针对这一问题,本文提出了一种适用于同步重建过程的采样模式生成方案.考虑到MRI信号的特点(MRI信号能量主要集中在k空间低频区域,k空间高频区域系数小、低频区域系数大),采样过程中优先采集低频区域信号,不仅可以尽早地得到质量较好的图像,而且也可以在采集同样数目相位编码行的条件下得到最优的图像,提高图像质量的收敛速度.
1 基本理论 1.1 CS 理论磁共振图像是由k空间数据经过反傅里叶变换获得的.为了得到正确的磁共振图像,需要在满足奈奎斯特定理的条件下采集完整的k空间数据[12].如果采样的频率过低,则图像中会出现卷褶伪影;如果采样频率足够高,但减少采集数据点的总数,则图像的分辨率会降低[13].而利用CS方法,可以对k空间进行随机的欠采样,在采样的总量远低于奈奎斯特采样定律要求的情况下,通过非线性重建方法来重建出图像.根据CS思想:只需要采集k空间的一个随机子集y,则图像x可以由下面的约束优化问题求解出来:
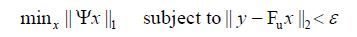 (1)
(1)
(1)式第一项表征图像的稀疏性,其中:x为待重建的图像,Ψ为稀疏变换(如小波变换),
如果用小波变换和全变分(total variation,TV)变换来表示图像的稀疏性,并转化为非约束问题,则能量函数为:
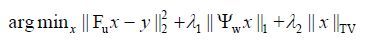 (1)
(1)
(2)式中Ψ泛指描述稀疏变换,Ψw是稀疏变换的一种方法,用来描述小波变换.其中,稀疏变换影响着最终重建图像的质量、自适应的稀疏表示,如基于图像块的方向小波(patch-based directional wavelets,PBDW)[14]和基于图像块的非局部算子(patch-based nonlocal operator,PANO)[15]等方法可以明显地提高重建图像的质量.本文从重建时间的角度上考虑,采用最常用的小波变换和TV变换作为稀疏变换.
(2)式为凸优化问题,解决这类最小化问题的方法有很多,如共轭梯度法[5]、分裂布雷格曼方法[10]和二级布雷格曼-字典更新算法[16].本文使用的是分裂布雷格曼方法,相关参数如下:外循环10次,内循环2次,TV项权重系数为4,保真项权重系数为20,小波项权重系数为47;以上参数是我们在实验中改变所有可能参数得到较好重建结果对应的一组参数.
1.2 同步重建过程中的动态采样方案传统的CS-MRI根据形如(3)式的多项式型PDF函数生成欠采样模式[17]:
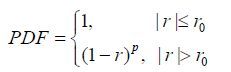 (3)
(3)
其中,r表示k空间待采集的相位编码行到k空间中心的距离,r0表示k空间全采样中心的半径.r0越大,k空间中心区域采样的相位编码行越多.p为正实数,用于调节k空间外部区域的相位编码行被采到的概率.p越大,k空间边缘部分被采到的概率越小,靠近中心区域被采到的相位编码行越多.在采样率不变的情况下,r0和p都是可调整的参数.
也可以利用如(4)式的高斯型PDF函数来生成欠采样方案:
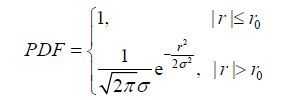 (4)
(4)
其中,r与r0的意义均与(3)式相同;σ用于调节k空间外部区域的相位编码行被采到的概率,σ越大,边缘部分被采到的概率越大,靠近中心区域被采的相位编码行越少.
常用PDF函数的形式如图 2所示,其中横坐标为r,纵坐标PDF表示k空间各个相位编码行被采到的概率.
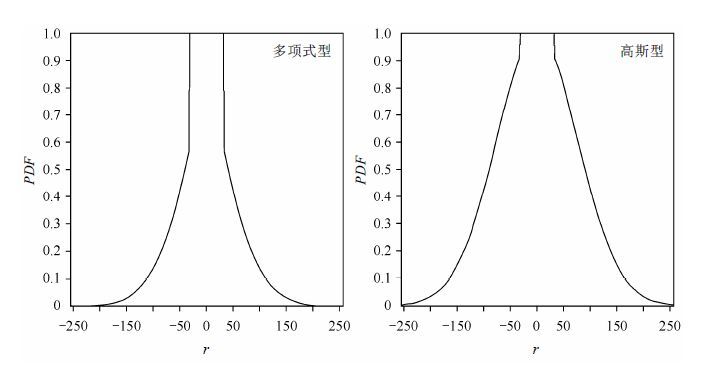
|
| 图2 多项式分布型PDF 和高斯分布型PDF Fig.2 PDFs of polynomial and Gaussian distribution |
上述方法根据固定的采样率来生成PDF函数,而由于同步重建过程中,可以根据重建图像质量来决定何时终止采样,并没有一个固定不变的采样率,所以传统的采样模式生成方法并不完全适用.为此,本文提出了一种适用于同步重建的动态采样方案,具体实现过程如图 3所示.
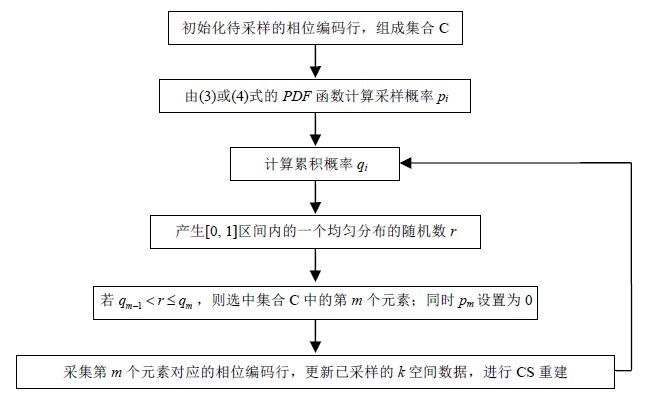
|
| 图3 同步重建过程中的动态采样模式 Fig.3 Dynamic sampling scheme in synchronized scanning-reconstruction |
首先初始化待采样的相位编码行索引值集合C,对于C中的每个元素i,根据选定的PDF计算对应的采样概率pi,并由此计算出对应的累积概率qi;其次在[0,1]区间内产生一个均匀分布的随机数r,若随机数r满足
MRI信号的k空间低频区域反映了图像的轮廓,k空间高频区域反映了图像的细节信息,使用单一的变密度采样模式可以生成高频低频适当分布的k空间采样模式[18].但是MRI信号能量主要集中在k空间低频区域,对图像重建的影响更大,我们发现,在同步扫描重建过程中,为了得到更好的图像质量,可以采用分段变密度采样模式[20].即把采样过程分为两个阶段,第一个阶段使用相对集中的PDF优先采集低频区域信号,第二个阶段使用相对发散的PDF,适当增加高频区域相位编码行被选中的概率.实验结果证明,与使用单一PDF的采样方法相比,使用分段式采样方案能够在相同采样率下获得更好的重建效果.
2 实验部分与结果分析 2.1 实验条件本文利用前述采样模式生成方案进行了同步重建过程的模拟实验.实验数据来源于上海卡勒幅磁共振技术有限公司的Sapphire 1.5 T超导型MRI系统,原始数据是基于自旋回波序列扫描得到的维度为512×512的真实脑图,本文所用的数据是单个通道的数据,所以图像整体灰度并不均匀.图 4(a)所示为全采样k空间的模图数据,图 4(b)所示为全采样k空间数据的傅里叶变换后的图像.
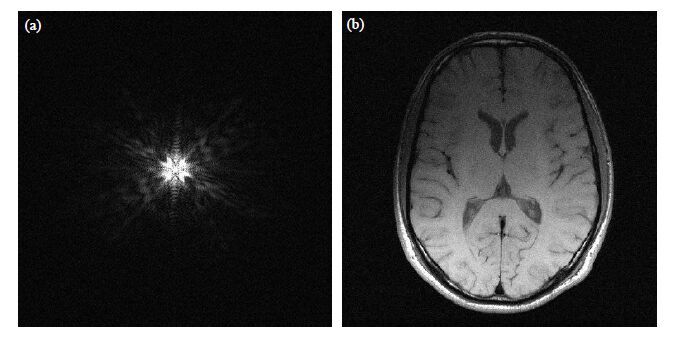
|
| 图4 (a) k 空间数据及其(b)傅里叶变换后的横断位脑图 Fig.4 (a) k-space data and (b) their corresponding brain image |
实验中,频率编码方向完整采样,相位编码方向按照前文所述采样模式生成方案进行采样.具体过程如下:先采集k空间中央连续64行数据(采样率为12.5%),然后启动同步扫描重建过程,开始CS重建,同时根据采样模式不断采集新的数据,并将新的数据加入重建所用的数据中,如此往复,直到整个过程结束.重建算法使用分裂布雷格曼算法,采用4级小波变换,小波基为Db4.
图 5为动态采样模式部分模拟实验的结果,模拟采样率达到12.5%、20%、30%和50%时的同步重建获得的结果以及它们与完全采集后傅里叶变换所得的差异图.可以看出,随着采样的进行,图像重建的质量不断提高.采样率达到30%以上时,图像质量基本可以满足临床应用需要.
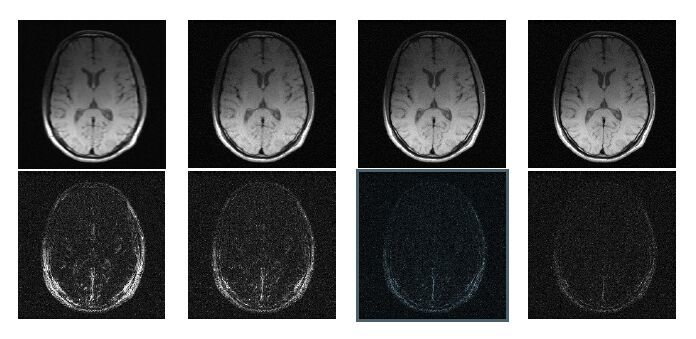
|
| 图5 同步重建中不同采样率下的重建图(上)和差异图(下,均放大10 倍),从左到右采样率分别为12.5%、20%、30%和50% Fig.5 The reconstructed images (upper) and their corresponding difference images (lower, 10×) when the sampling ratio reaches 12.5%、20%、30% and 50% respectively |
我们也对重建图像质量进行了定量分析.由于采样过程的随机性,为更加准确地定量比较重建结果,对不同的采样过程,均进行100次重复试验,对结果做统计分析.我们利用峰值信噪比(peak signal to noise ratio,PSNR)来定量比较重建图像质量.假设图像大小为,高分辨率图像为,重建图像或填零图像为,则均方根误差(MSE)和PSNR定义为:
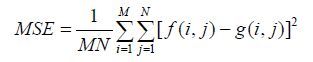 (5)
(5)
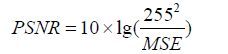 (6)
(6)
图 6显示了基于高斯分布型(σ=0.1×512,即方差σ为相位编码步的10%)和多项式分布型(p=2)的PDF函数进行同步扫描重建的结果.从图中可以看出,在两种不同的采样模式下,随着采样的进行,PSNR均值都会不断提高,显示图像质量随着同步扫描重建的进行不断改善.在大部分时间中,采用高斯分布型的PDF进行采样获得的图像重建效果较好,但当采样率接近50%时,两种采样模式的结果差别不大.综合这两部分的结果,可知同步扫描重建方案基本可行,随着扫描的进行,重建的图像质量稳定改善;同时,使用不同的PDF对重建结果有影响.
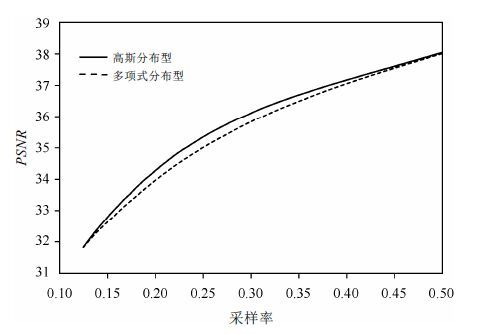
|
| 图6 PSNR 均值随采样率的变化 Fig.6 Changes of average PSNRs with the sampling ratios |
为了在采样过程中获得质量更好的图像,本文提出了分段变密度采样模式.我们将同步采集重建过程划分为两个阶段:第一阶段为密集采集k空间低频部分,第二阶段为稀疏采集k空间高频部分;在采样率达到30%以前为采样第一阶段,基于方差σ=0.15×512的高斯型PDF进行动态采样;采样率达到30%直至终止条件为采样第二阶段,基于σ=0.15×512的高斯型PDF进行采样.这两种不同的高斯型分布PDF如图 7(a)和7(b)所示,另外此过程同样利用分裂布雷格曼方法来重建图像.

|
| 图7 (a) σ= 0.1×512 的高斯型PDF;(b) σ= 0.15×512 的高斯型PDF Fig.7 (a) PDF of Gaussian (σ= 0.1×512 ); (b) PDF of Gaussian (σ= 0.15×512 ) |
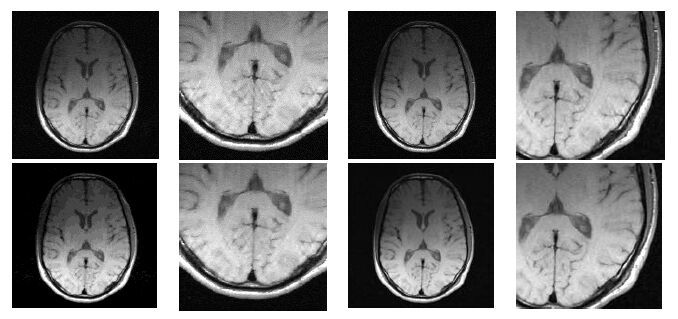
我们分别对基于高斯分布型的单一PDF采样(σ=0.15×512)和高斯分布型的分段式采样和(σ=0.1×512和σ=0.15×512)的结果进行了比较,图 8所示是模拟采样率为20%和35%时的CS重建图以及主要部分细节图.从图中可以看出,分段式采样模式重建的图像质量较好,伪影较少,在35%的采样率下的图像质量可以满足临床应用的需要.
|
| 图8 单一PDF 与分段式采样模式下的重建效果比较,上面一排是采用单一PDF 重建的结果,下面一排是采用分段采样模式重建的结果,采样率分别为20%(左一和左二)、35%(右一和右二) Fig.8 The reconstructed images and detailed images using single PDF and two-phase sampling schemes respectively. Upper: reconstucted images from single PDF. Lower: reconstructed images from two-phase sampling scheme. The sampling ratios are 20% (the left two figures) and 35% (the right two figures) respectively |
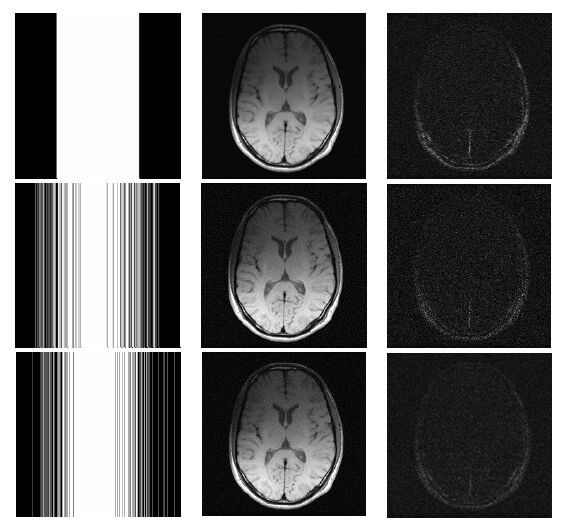
k空间中心决定了图像的PSNR和对比度,这部分数据对图像质量有重要影响,我们的两段式采样方案的第一阶段优先采集k空间中央的数据.图 9比较了两种随机采样模式与k空间中央连续采集的结果.这里的k空间中心连续采样是指按照连续的采样顺序,一边采集k空间中心区域的相位编码行,一边通过CS算法进行重建.根据我们的实验,即使采用中央连续采样的方式,CS算法重建的结果也显著优于填零后直接进行傅里叶变换的结果.从图中可以看出,与中央连续采集方式相比,两种随机欠采模式都更好地保留了图像的细节,重建图像质量较高.
|
| 图9 三种采样方案的实验结果比较.从左到右分别是采样所用的模板、重建图像以及重建图像与全采样傅里叶变换的结果的差异图(放大10 倍);上面一排是k 空间中心连续采样的结果,中间一排是单一PDF采样的结果,下面一排是分段采样的结果 Fig.9 Comparison of the results of three different sampling schemes. From left to right are sampling masks, reconstructed images and the difference images (×10) respectively. Upper: center-continuous sampling scheme (sampling from the center to the outside); Middle: single PDF scheme; Bottom: two-phase scheme |
我们也对三种采样模式进行了定量比较,同样,对于随机采样模式,我们将实验重复进行100次,将PSNR均值作为分析依据.图 10为三种采样方案重建的PSNR随采样率的变化情况.从图中可以看出,随着采样率的变化,不同的采样方式的重建结果均稳定改善,而采用分段采样方案的重建结果在整个采样过程中,重建结果均优于其余两种方案.

|
| 图10 三种不同的采样方案PSNR 均值随采样率的变化 Fig.10 Changes of average PSNRs of three different schemes with the sampling ratio |
本文提出了同步扫描采集方案,通过将CS的迭代重建过程与采样过程结合,缩短了MRI重建所需的时间,同时在扫描的过程中可以向用户显示图像,在一定程度上克服了CS-MRI图像重建质量不稳定的问题[23].本文同时提出了适用于该同步扫描采集方案的分段式采样方案,实验结果表明,该采样方案在不同的采样率下均能获得更好的重建结果.本文的结果表明,CS-MRI的同步重建方案具有可行性,为CS-MRI的临床应用提供了一种动态MRI之外的新途径.
| [1] | Chang C H, Ji J. Compressed sensing MRI with multichannel data using multicore processors[J]. Magn Reson Med, 2010, 64(4):1135–1139. |
| [2] | Candès E J. Proceedings of the International Congress of Mathematicians[C]. Madrid:J Eur Math Soc, 2006. |
| [3] | Donoho D. Compressed sensing[J]. IEEE T Inform Theory, 2006, 52(4):1289–1306. |
| [4] | Tsaig Y, Donoho D L. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3):549–571. |
| [5] | Cande's E J, Romberg J K, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Commun Pure Appl Math, 2006, 59(8):1207–1223. |
| [6] | Lustig M, Donoho D, Pauly J M. Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med, 2007, 58(6):1182–1195. |
| [7] | Lustig M, Santors J M, Donoho D L, et al. k-t Sparse:High frame-rate dynamic MRI exploiting spatio-temporal sparsity[J]. Proc Annu Meeting ISMRM, 2006:2420. |
| [8] | Nam S, Akcakaya M, Basha T, et al. Compressed sensing reconstruction for whole-heart imaging with 3D radial trajectories:A graphics processing unit implementation[J]. Magn Reson Med, 2013, 69(1):91–102. |
| [9] | Candes E J, Romberg J K, Tao T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE T Inform Theory, 2006, 52(2):489–509. |
| [10] | Goldstein T, Osher S. The split Bregman methods for L1 regularized problems[J]. SIAM J Imaging Sci, 2009, 2(2):323–343. |
| [11] | Smith D, Gore J, Yankeelov T, et al. Real-time compressive sensing MRI reconstruction using GPU computing and split Bregman methods[J]. Int J Biomed Imaging, 2012doi:10.1155/2012/864827. |
| [12] | Sung K, Hargreaves B A. High-frequency subband compressed sensing MRI using quadruplet sampling[J]. Magn Reson Med, 2013, 70(5):1306–1318. |
| [13] | Tsai C M, Nishimura D G. Reduced aliasing artifacts using variable density k-space sampling trajectories[J]. Magn Reson Med, 2000, 43(3):452–458. |
| [14] | Qu X B, Guo D, Ning B D, et al. Undersampled MRI reconstruction with patch-based directional wavelets[J]. Magn Reson Imaging, 2012, 30(7):964–977. |
| [15] | Qu X B, Hou Y K, Lam F, et al. Magnetic resonance image reconstruction fromundersampled measurements using a patch-based nonlocal operator[J]. Med Image Anal, 2014, 18(6):843–856. |
| [16] | Liu Q G, Wang S S, Yang K, et al. Highly undersampled magnetic resonance image reconstruction using two-level Bregman method with dictionary updating[J]. IEEE T Med Imaging, 2013, 32(7):1290–1301. |
| [17] | Vellagoundar J, Reddy M R. Optimal k-space sampling scheme for compressive sampling MRI[J]. IECBES, 2012doi:10.1109/IECBES.2012.6498108. |
| [18] | Liu D D, Liang D, Liu X, et al. Under-sampling trajectory design for compressed sensing MRI[J]. IECBES, 2012doi:10.1109/EMBC.2012.6345874. |
| [19] | Ravishankar S, Bresler Y. Adaptive sampling design for compressed sensing MRI[J]. Conf Proc IEEE Eng Med Biol Soc, 2011doi:10.1109/IEMBS.2011.6090639. |
| [20] | Yang Y, Liu F, Xu W L, et al. Compressed sensing MRI via two-stage reconstruction[J]. IEEE Trans Biomed Eng, 2015, 62(1):110–118. |
| [21] | Kutyniok G. Theory and applications of compressed sensing[J]. GAMM-Mitteilungen, 2013, 36(1):79–101. |
| [22] | Lustig M, Donoho D L, Santos J M, et al. Compressed sensing MRI[J]. IEEE Signal Proc Mag, 2008, 25(2):72–82. |
| [23] | Lustig M, Donoho D, Santos J M, et al. A look at how CS can improve on current imaging techniques[J]. IEEE Signal Proc Mag, 2008, 24(2):72–82. |
 2016, Vol. 33
2016, Vol. 33



