文章信息
- 陶泉, 贺玉贵, 王超, 冯继文, 陈方, 刘朝阳
- TAO Quan, HE Yu-gui, WANG Chao, FENG Ji-wen, CHEN Fang, LIU Chao-yang
- TM110模式DNP探头的研制与应用
- A TM110 Dynamic Nuclear Polarization Probe: Design and Applications
- 波谱学杂志, 2016, 33(1): 44-53
- Chinese Journal of Magnetic Resonance, 2016, 33(1): 44-53
- http://dx.doi.org/10.11938/cjmr20160104
-
文章历史
- 收稿日期: 2015-05-06
- 收修改稿日期: 2016-01-23
2. 中国科学院大学, 北京 100049;
3. 武汉光电国家实验室(筹), 华中科技大学 光学与电子信息学院, 湖北 武汉 430074
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Wuhan National Laboratory for Optoelectronics, School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China
自1946年,美国科学家Bloch和Purcell各自独立发现宏观物质的核磁共振(nuclear magnetic resonance,NMR)现象以来,经过近70年的发展,NMR技术已作为一种重要的分析手段广泛应用于物理、化学、生物和医学等领域.但与其他谱学方法相比,NMR技术一个明显的不足之处就是其检测灵敏度非常低.而基于NMR理论发展起来的磁共振成像(magnetic resonance imaging,MRI)技术也面临同样的问题.如何提高NMR和MRI的检测灵敏度一直是磁共振领域研究人员所努力的方向.NMR和MRI的检测灵敏度与核极化度P成正比,通常情况下,在外磁场B0中热平衡时,核极化度P非常小,从而导致了NMR和MRI的检测灵敏度非常低.外磁场中热平衡时,核极化度P满足如下关系:

其中γ为检测原子核的旋磁比,h为普朗克常数(Planck constant),k为玻尔磁曼常数(Boltzmann constant)常数,T为温度.由(1)式可以看出,增加磁场强度B0可以提高核极化度,从而改善NMR的探测灵敏度.在过去的近五十年中,NMR技术主要沿这个方向发展,目前超导磁体已提高到接近极限强度的23.5 T(相应的质子共振频率为1 000 MHz).但即使在这样高的磁场条件下,原子核的极化度依然很小,例如室温热平衡时,质子1H极化度仅约为0.8×10-4,也就是约每1万个质子中只有不到1个质子的核自旋对NMR信号有贡献.此外,由于技术和生理学等方面的原因,全身的MRI断层影像技术还无法像NMR技术那样在很高的磁场强度下实现,这使得灵敏度低的问题在MRI领域中更为突出[1].因而必需探索其它的提高核极化度的技术.动态核极化(Dynamic Nuclear Polarization,DNP)[2, 3]因其可以极大地增强NMR信号而引起了人们的广泛关注.DNP是一种电子与核的双共振技术,通过微波照射来饱和自由基中的未配对电子,由于电子与相邻核之间存在耦合作用,使得与其相耦合的核能级布居数发生变化,把电子的高自旋极化度转移到核上,使核自旋获得高极化度,从而达到提高NMR检测灵敏度的效果.利用DNP技术,质子最大极化增强达660倍;13C原子核最大增强能达2 600倍.由于DNP突出的极化增强效果,通过DNP技术提高NMR检测灵敏度是目前NMR和MRI领域的研究热点,然而,目前市场上还非常缺乏功能完备的新型DNP-NMR/MRI系统设备,这已成为开展DNP相关研究的瓶颈.因而,设计与研制具有自主知识产权的DNP-NMR/MRI系统有极其重要的科研和商业价值.
DNP探头是DNP系统的一个关键部件,其性能指标直接关系到DNP增强效果,而国内关于DNP探头设计与研制鲜见报道.本研究首先由理论分析与计算,选择X波段的TM110模式圆柱形谐振腔为激发电子顺磁共振(EPR)的微波部件,进一步通过Ansoft-HFSS软件对DNP探头进行具体的仿真设计,然后对加工制作的谐振腔进行电性能调试,最后在自主研制的0.35 T的DNP-NMR/MRI系统上进行上机实验测试,验证本研究DNP探头设计与研制方案的可行性,为进一步开展DNP探头相关技术的研究积累经验.
1 DNP探头 1.1 TM110模式圆柱形谐振腔微波谐振腔作为最常见微波谐振结构,已广泛应用于EPR和ENDOR(电子-核双共振,EPR检测)探头中来激发电子顺磁共振[4, 5, 6, 7],而核的激发则是通过射频线圈来实现.在DNP探头设计中,要求微波磁场与射频磁场皆垂直于外部静磁场并具有一定的均匀度;在尽可能增大样品区域微波与射频磁场的同时,还应减小其电场分量以减小其加热效应,因为微波的电场分量对样品的加热效应起主导作用.目前,常见的微波金属谐振腔有:矩形TE102模式、圆柱形TE011模式和圆柱形TM110模式.TE102矩形谐振腔中心存在一个磁场最强、电场为零的矩形面,因此非常适合扁平样品管的实验,但其品质因数(Q值)低,一般只有几千;TE011模式圆柱形谐振腔虽然Q值很大,能到达 10 000~20 000,但只有轴线上磁场最强、电场为零;TM110模式圆柱形谐振腔也存在一个磁场最强、电场为零的矩形面,其Q值介于前面两种谐振之间,因此兼有两者的优点[8].用于激发核的射频线圈通常放于谐振腔内,射频线圈的引入不仅会影响到微波谐振腔的频率、Q值和模式分布等,还会对样品区域的微波场形成一定的屏蔽作用;常见于ENDOR中的射频线圈有双导线、亥姆霍兹线圈、螺线管和马鞍型线圈等.其中,螺线管激发效率高,产生的射频磁场均匀.为了能获得最佳的NMR信号灵敏度,我们采用TM110模式谐振腔,以螺线管作为核磁射频线圈,实现通过DNP增强技术来提高NMR和MRI相关实验检测灵敏度的目的.
1.2 TM110模式圆柱形谐振腔原理及设计圆柱形谐振腔作为DNP探头的关键组成部分,本质上是由一段长度为l的两端短路的圆波导构成,腔中振荡的电磁场分量可用圆波导的电磁场分量解[9]并考虑反射波而得到.由于圆波导中能传输TM和TE导波,圆柱形波导谐振腔中就存在TM和TE型模式.对于TMmnp模式的场分量[10]为:
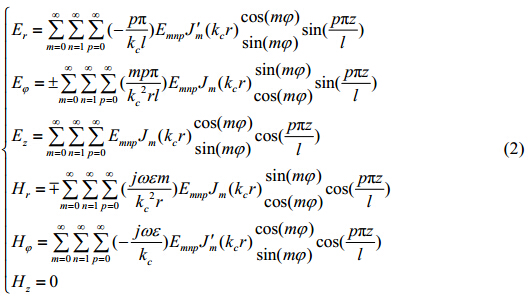
其中,波型指数m、n、p分别表示场沿圆周分布的驻波周期数、场沿半径分布的半波数或最大值个数、场沿轴向分布的半驻波数.${{J}_{m}}$、${{{J}'}_{m}}$分别表示第一类m阶贝塞尔函数及其导数.${{k}_{c}}=\frac{{{u}_{mn}}}{a}$,${{u}_{mn}}$为第一类m阶贝塞尔的第n个根,a为腔体半径.$\begin{matrix} \cos (m\varphi ) \\ \sin (m\varphi ) \\ \end{matrix}$表示导波场在φ方向存在$\cos (m\varphi )$和$\sin (m\varphi )$两种可能的分布,它们独立存在,相互正交,构成两极化简并模.对于TM110模,将m = 1、n = 1、p = 0带入(2)式可得:
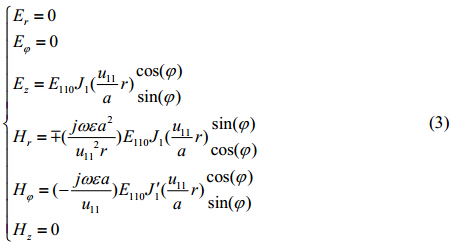
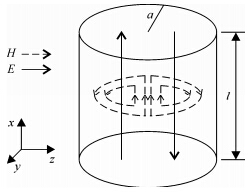
由以上(3)式场分量可得到TM110模式的场分布如图 1所示,由于p = 0,所以场分布沿轴线方向没有变化.
|
| 图 1 TM110模式圆柱形谐振腔场结构 Fig. 1 Field distributions in TM110 mode cylindrical cavity |
TMmnp模式圆柱形谐振腔的谐振频率为

进一步可写为

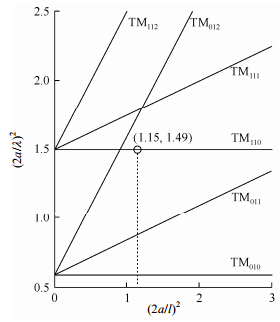
由(5)式可得到如图 2所示圆柱形谐振腔的模式图[10].由于通过合适的耦合孔来激励TM110模式时,不会激励起TE模式,因此不用考虑TE模式的干扰.根据此模式图便可初步确定腔体的尺寸.模式图中的交点表示模式简并,确定尺寸时应尽量避开这些交点.由(4)式可得

通过所需的谐振频率便可确定腔体半径.但由此得到的是空腔的尺寸,在加入射频线圈及其支撑结构后,谐振频率会偏小,因此,初步设计时频率应适当偏大些.
对于TMmnp模式谐振腔的Q值[11],可由下式求得

其中,δ为腔体的趋肤深度,S为常数因子,当p = 0时,S = 1;当p ≠ 0时,S = 2.
1.3 TM110模式圆柱形谐振腔仿真设计X-波段是EPR中最常用的频段,因此我们选择以X波段的TM110模式圆柱形谐振腔为例,利用Ansoft-HFSS软件对DNP探头进行具体的仿真设计.
通过前面的初步计算可知,当空腔半径为18 mm、长度为33.6 mm时,微波频率约为10 GHz.利用Ansoft-HFSS建模并进行求解,得到空腔的谐振频率与Q值,表 1给出了理论计算、仿真结果与实测的对比.我们可以看到,实测腔体Q值比仿真结果小了很多,主要原因是由于腔体内表面未作抛光处理,线圈表面光洁度不够,并且实测结果是在加入样品后所得,样品的介电损耗也会导致Q值降低.图 3为软件模拟的腔内磁场与电场分布.
| f /GHz | Q0 | |
| 空腔理论计算 | 10.16 | 17873 |
| 空腔仿真结果 | 10.3 | 17692 |
| 加入线圈等结构优化后仿真结果 | 9.871 | 2814 |
| 实测 | 9.856 | 1646 |

|
| 图 3 TM110模式谐振腔磁场(a)与电场(b)的仿真分布图 Fig. 3 Simulation of the distribution of magnetic(a) and electric(b)field in TM110 cavity |
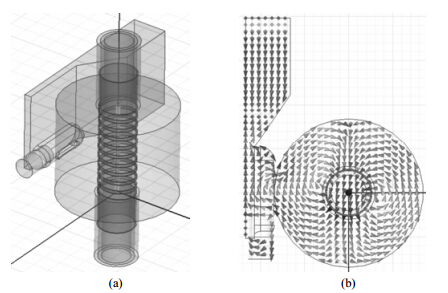
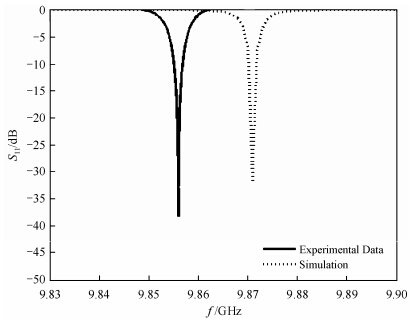
以上只是空腔的仿真计算,为实现电子-核双共振,还需加入螺线管作为射频线圈,同时还需线圈的支撑结构.微波信号通过耦合孔从BJ100波导耦合到腔内,耦合孔开于腔体侧壁上.考虑到磁体间隙尺寸的限制以及微波磁场需与外部静磁场垂直等问题,我们通过波导宽边耦合,并且沿着窄边形成一段渐变结构.波导与腔体间的耦合度通过移动一个小铜块改变耦合孔的大小来调节.图 4是探头完整仿真模型及其波导端口激励下截面磁场分布.通过仿真优化,腔体最终尺寸为:半径16.8 mm、长27 mm.图 5为优化后反射系数(S11)的仿真结果及实测结果.
|
| 图 4 TM110模式谐振腔完整模型(a)与波端口激励下的磁场分布(b) Fig. 4 The model of TM110 cavity(a) and magnetic field distribution under wave port excitations(b) |
|
| 图 5 TM110模式谐振腔S11参数仿真与实测结果 Fig. 5 Simulated and experimental data of S11 parameter of TM110 cavity |
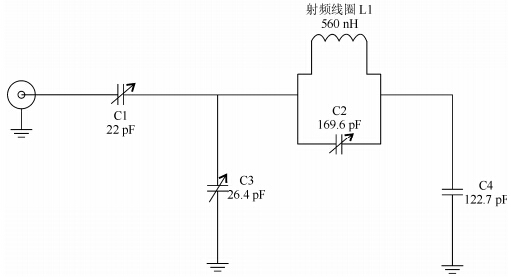
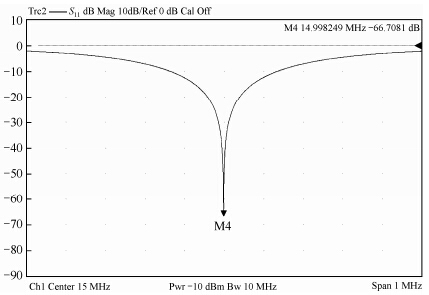
作为DNP探头的另一重要组成部分,射频线圈用于激发核磁共振.在同一外部静磁场下,质子的共振频率约是电子共振频率的1/657.5.根据以上设计的谐振腔频率,其对应所需的核磁共振线圈谐振频率约为15 MHz,上述谐振腔中射频线圈的电感约为560 nH,为了改善螺线管因波长效应引起的射频B2场不均匀性,同时兼顾射频功率的激发效率,我们采用图 6所示并联的L-C平衡电路[12].其中,C2用于调谐,C1、C3和C4用于调节匹配.图 7为实测核磁共振射频线圈的S11参数.
|
| 图 6 射频线圈调谐匹配电路 Fig. 6 Tuning and matching circuit of RF coil |
|
| 图 7 射频线圈S11实测参数 Fig. 7 S11 experimental parameter of RF coil |
常用的腔体加工材料一般分为三种类型[7]:(1)高阻抗金属或合金,如不锈钢、银镍合金等;(2)无机介质材料,如石英、陶瓷、玻璃;(3)有机介质,如环氧化合物.非金属材料加工的腔体需要在其表面镀金或银.为了提高金属腔体的Q值,其表面需抛光并镀金或银[13],由于银易氧化,因此常在镀银后再镀一层金加以保护.图 8所我们实际加工制作的DNP探头,谐振腔部分采用黄铜H62并镀银;弯波导为BJ100标准H面弯波导;射频线圈由厚0.3 mm、宽0.9 mm的铜带绕成10圈28 mm长的螺线管组成,镀银后固定于石英玻璃管外壁上,线圈两端通过带弹簧探针的射频接头与外部调谐匹配电路连接.

|
| 图 8 DNP探头实物 Fig. 8 DNP probe |
为了验证本设计探头的可行性,我们在本实验室自主研发的场强为0.35 T的X波段DNP-NMR/MRI系统上进行了实验验证.实验使用直径为1 mm的样品管,浓度为10 mmol/L的TEMPOL水溶液样品,微波频率为9.856 49 GHz,微波功率为50 W.结果(图 9)显示:我们得到了50倍以上增强的质子信号.其中,图 9(a)为关闭微波发射机后得到的质子信号谱图,图 9(b)为打开微波发射机后测得的质子信号谱图.

|
| 图 9 无微波(a)和有微波(b)照射下测得的TEMPOL水溶液样品质子信号谱图 Fig. 9 1H NMR spectra of the TEMPOL solution sample with(b) and without(a)microwave irradiation |
为了对比有无DNP增强下的MRI图像,我们同时还对上述TEMPOL水溶液进行了成像实验.应用自旋回波MRI成像序列,重复时间TR设定为1 500 ms,回波时间TE设定为20 ms,微波频率为9.856 49 GHz,微波功率为50 W,我们得到了图 10所示两幅图像,其中,图 10(a)为关闭微波发射机以后得到的MRI图像,图 10(b)是打开微波发射机后得到的MRI图像.对比可知,通过DNP增强,能够极大的提高图像的信噪比.

|
| 图 10 无微波照射下(a)和有微波照照射下(b)的TEMPOL水溶液MRI图像 Fig. 10 MR Imaging of the TEMPOL solution sample with(b) and without(a)microwave irradiation |
通过对TM110谐振腔的初步理论计算到探头结构的仿真设计,得到了一个优化的DNP探头结构,并加工制作了探头实物.利用矢量网络分析仪对探头进行电性能测试,其S11参数与仿真结果较为吻合;实测Q值与仿真相比偏低很多,是由射频线圈及其支撑结构实际损耗较大和腔体内表面及线圈表面光洁度不够导致.最后,在本实验室自主研发的场强为0.35 T的X波段DNP-NMR/MRI系统上进行了上机实验,设计制作的DNP探头在1H NMR实验中获得了大于50倍的信号增强,同时,在MRI实验中获得了DNP增强后的图像,验证了本研究DNP探头设计与研制方案的可行性,为进一步开展DNP探头相关技术的研究积累了经验.
| [1] | Krummenacker J G. Dynamic Nuclear Polarization for Magnetic Resonance Imaging: An In-bore Approach[D]. Frankfurt: University of Frankfurt, 2012. |
| [2] | Overhauser A W. Polarization of nuclei in metals[J]. Phys Rev, 1953, 92(2): 411-415. |
| [3] | Maly T, Debelouchina G T, Bajaj V S, et al. Dynamic nuclear polarization at high magnetic fields[J]. J Chem Phys, 2008, 128(5): 052211. |
| [4] | Kay C W M, Grishin Y A, Weber S, et al. An improved TM110 resonator for continuous-wave ENDOR studies at X-band[J]. Appl Magn Reson, 2007, 31(3): 599-609. |
| [5] | Christidis T C, Heineken F W. A cylinder TM110 ENDOR cavity[J]. J Phys E: Sci Instrum, 1985, 18(4): 281-283. |
| [6] | Christidis T C, Heineken F W. A microwave cavity for high power ENDOR spectroscopy[J]. J Phys E: Sci Instrum, 1972, 6(5): 432-434. |
| [7] | Chacko V P. “Wonderstone” ENDOR cavity[J]. Rev Sci Instrum, 1978, 49(7): 1 012-1 014. |
| [8] | Lu Jing-fen(卢景雰). Advanced Electron Paramagnetic Resonance Spectroscopy and Its Applications(现代电子顺磁共振波谱学及其应用)[M]. Beijing(北京): Peking University Press(北京大学出版社), 2012. |
| [9] | Liao Cheng-en(廖承恩). Basis of Microwave Technique(微波技术基础)[M]. Xian(西安): Xidian University Press(西安电子科技大学出版社), 1994. |
| [10] | Zhang K Q, Li D J. Electromagnetic Theory for Microwaves and Optoelectronics (2nd) [M]. Berlin: Springer-Verlag, 2007. |
| [11] | Wang Wen-xiang(王文祥). Microwave Engineering Technology(微波工程基础)[M]. Beijing(北京): National Defense Industry Press(国防工业出版社), 2009. |
| [12] | Mao Wen-ping(毛文平). Hardware Development for High-Field NMR(高场核磁共振波谱仪硬件的研究)[D]. Wuhan(武汉): Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences(中国科学院武汉物理与数学研究所), 2012. |
| [13] | Wen Xu-jie(温旭杰), Huang Pu(黄璞), Geng Jian-pei(耿建培), et al. Design of rectangular and planar microresonators for X-band pulsed EPR spectrometer (X波段脉冲电子顺磁共振谱仪的矩形谐振腔与微型平面腔的设计)[J]. Chinese J Magn Reson(波谱学杂志), 2011, 28(4): 437-446. |
 2016, Vol. 33
2016, Vol. 33