文章信息
- 田佳欣, 刘文卿, 宋艳红, 轩亚楠, 李军方, 姚叶锋, 魏达秀
- TIAN Jia-xin, LIU Wen-qing, SONG Yan-hong, XUAN Ya-nan, LI Jun-fang, YAO Ye-feng, WEI Da-xiu
- 利用仲氢诱导极化技术实现Deutsch算法
- Implementation of Deutsch Algorithm Using Para-Hydrogen Induced Polarization
- 波谱学杂志, 2015, 32(4): 618-627
- Chinese Journal of Magnetic Resonance, 2015, 32(4): 618-627
- http://dx.doi.org/10.11938/cjmr20150407
-
文章历史
- 收稿日期:2015-03-02
- 收修改稿日期:2015-11-03
2. 中国科学院 上海有机化学研究所,上海 200032
2. Shanghai Institute of Organic Chemistry, Shanghai 200032, China
热平衡态时,处于高磁场中的原子核各能级上的粒子数满足玻尔兹曼分布,以自旋量子数I = 1/2的核为例,其高低能级上的粒子数差为$\Delta n \cong {{\gamma \hbar {H_0}} \over {2kT}}$,$\gamma $为旋磁比,H0为磁场强度,T为体系的温度.以氢核为例,当H0 = 2.35 T时,粒子数差$\Delta $n约为10-5 N(N为总的粒子数).$\Delta $n的大小与核磁共振的信号强度成正比,常温下,$\Delta $n的数值较小,导致核磁共振信号的灵敏度较低.为了提高灵敏度,方法之一是提高主磁场的强度,但其对硬件的要求较高,且谱仪造价昂贵,难以普及.因此人们发展了各种超极化的方法,如激光光泵(Optical Pumping,OP)、动态核极化(Dynamic Nuclear Polarization,DNP)、仲氢诱导核极化(Para-Hydrogen Induced Polarization,PHIP)[19]等,这些技术可以将核自旋的极化度提高4~5个量级.
在众多用于实现量子信息和量子计算的物理体系中,核磁共振[20]是进行量子计算实验时取得进展尤为突出的方法之一.其优点是核自旋体系具有较长的相干时间,可使用已经非常成熟的脉冲控制技术对核自旋进行相干操控.但核磁共振体系也具有一定的局限性[23],如信号本身的低灵敏度、随量子数增加信号呈指数下降[24]的信噪比等因素限制了量子位数的扩展[25].通常的量子信息任务首先需要制备量子计算的初始态-赝纯态[26, 27],其积算符形式可以表示为:

(1)式中${1 \over {{2^n}}}$是n自旋体系的最大混合态,$\varepsilon $是态的极化度.高温近似条件下,随着量子位数的增多,赝纯态的信号强度是指数下降的.文献[28]研究表明,极化度太低时(两自旋体系中,临界值为$\varepsilon = {1 \over 3}$),自旋体系处于混合态,导致利用赝纯态制备的纠缠态实际上是分离态;之后,文献[29]讨论了密度矩阵的不同定义,建议使用完全密度矩阵、压缩密度矩阵和约化密度矩阵分别描写一个封闭量子体系的,提出具有相同压缩密度矩阵但是成分不同的系综可以通过系综整体测量来区别,指出通过分析压缩密度矩阵而认为核磁共振量子计算中没有纠缠的结论是没有根据的.另外,为了避免核磁共振量子计算中 的纠缠存在与否的争议问题,人们提出了各种方案制备纯态,仲氢诱导极化技术通过选择处于纯度极高的仲氢分子与合适的样品分子发生加成反应,将仲氢分子的极化度转移到样品分子中.该方法已经被应用于制备核磁共振中的纯态及实现量子算法[29, 30].本文将仲氢诱导极化技术得到的氢原子用于量子计算,分别实现了两量子位的Deutsch-Jozsa[26, 31]算法和三量子位的Deutsch-Like算法[31].实验结果表明,诱导极化技术能直接得到量子计算的纯态,同时信号强度显著增强.
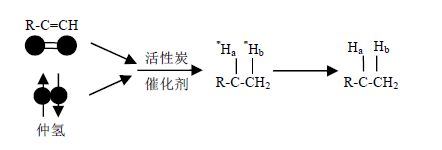
1 基本理论 1.1 仲氢诱导极化氢气分子的对称性结构导致其存在两个自旋同分异构体,也就是核自旋指向相同的正氢和核自旋指向相反的仲氢.仲氢的整个自旋量子数为I = 0,是一个单重态;正氢的整个自旋量子数为I = 1,是一个简并的三重态.仲氢和正氢的含量比是一个与体系温度有关的函数,高温条件下,仲氢和正氢含量的相对比率近似为1∶3;低温条件下,仲氢的含量比例不断增加,在77 K条件下可以得到50%的仲氢,温度降到20 K时,能够得到近乎纯的仲氢.核自旋不同能级之间跃迁速度比较缓慢,通过使用合适的催化剂可以加快能级之间的跃迁,除去催化剂回到室温后,由于部分能级之间不满足跃迁规则,得到的高纯度的仲氢处于比较稳定的状态.这种高纯度的仲氢分子能够在合适催化剂的作用下与不饱和化合物分子发生加成反应,形成新的化合物,并且加成进去的两个氢核具有极高的极化度,在外界的作用下处于一定的初始态.反应过程如图 1所示,根据加氢合成反应时体系所处的环境的不同,存在PASADENA[32]和ALTADENA[1]两种反应过程,即仲氢和不饱和分子的反应在高磁场中进行时为PASADENA;反之,若反应在低磁场中进行时为ALTADENA.
|
| 图 1 超氢反应的过程 Fig. 1 Scheme of the parahydrogenation |
仲氢的密度矩阵形式:

加氢反应经过时间$t > > {1 \over k}$后,密度矩阵演化为:
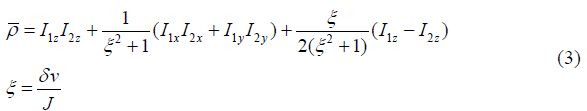
PASADENA条件下,自旋系统属于AX体系,外磁场较强时,$\xi > > 1$,密度算符变为:

ALTADENA条件下,其解析分析较复杂,加氢之后将体系放入磁体中,自旋系统只有AX体系中的$|01\rangle $态或者$|10\rangle $态,对应的密度算符变为:
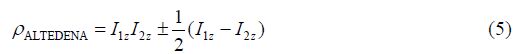
考虑一个两自旋同核系统,在高温近似条件$kT > > \gamma {B_0}$下,对处理热平衡态下的核自旋施加一个90°y硬脉冲后,体系的密度矩阵可近似表示为:

处于ALTADENA条件下与处于热平衡态时能观测到的信号强度比为$\eta = {2 \over A}$.室温下,处于磁场中共振频率为400 MHz的质子的约为30 000,因此利用仲氢诱导极化技术能极大地提高探测核的信号强度.PASADENA条件下,其信号增强与ALTADENA条件类似,但由于状态$|01\rangle $和$|10\rangle $都被极化,所以PASADENA条件下的信号增强最终是ALTADENA条件下的一半.
由以上分析可知,仲氢诱导极化技术能极大地提高核自旋的信号强度,并且利用仲氢诱导极化技术得到的初态与量子计算中通常运用的初态相似,这样可以直接实现一系列的量子计算任务,避免因制备赝纯态产生的信号衰减.
1.2 仲氢诱导极化技术实现Deutsch-Jozsa算法[2]和Deutsch-Like算法[3]Deutsch-Jozsa(D-J)算法解决问题的数学表述为:设f是集合${\{ 0,\,\,1\} ^n}$映射到集合{0,1}的Boolean函数,其中n是输入比特的个数,N = 2n,算法要解决的问题是判断所给映射函数是平衡函数还是常函数,这两种函数的定义为:
(1) 常函数:对于集合${\{ 0,\,\,1\} ^n}$中的所有元素i,$f(i)$全为0或者全为1.
(2) 平衡函数:集合${\{ 0,\,\,1\} ^n}$中的${2^n} - 1$个元素的输出函数$f(i) = 0$而其它输入.
以n = 1为例,要判断映射为平衡函数还是常函数,经典算法需要两步,即依次计算f (0)和f (1)的值,如果得到相同的输出结果,则可确定f为常函数,反之为平衡函数.
随着n的增加,经典算法所需的步数呈指数增加.利用量子力学中量子态的叠加性,Deutsch-Jozsa量子算法只需一步便可以判断出函数f的性质.当量子位初态为$|0\rangle \otimes |1\rangle $时,经过两个H门和一个Uf门的作用,最后第一个量子位的状态变为$|f(0) \oplus f(1)\rangle $,这样通 过测量第一个量子位的状态便可以判断出f是常函数还是平衡函数,具体的演化过程为:

Deutsch-like问题与D-J问题类似,区别在于Deutsch-like问题将输入与输出值的对应关系定义为:全为1;$2n - 1$个为1,一个为0;$2n - 1$个为1,另$2n - 1$个为0等等.并且把函数分为两类,一类称为奇函数,即对所有输入值,它们对应的输出值为1的个数是奇数;另一类称为偶函数,即输出值为1的个数为偶数.利用一种混合态为初态的量子算法能够通过一次运算得到函数的奇偶性[4].以一个三量子位体系[5]为例,其中一个量子比特为辅助位I0,算法的具体步骤为:
(1) 从热平衡态出发制备混合态${\rho _i}$,其中辅助位处于态$I_0^\alpha $,数据位处于4个状态的混合叠加.
(2) 构造算法将所需判断的函数信息包含进去.其过程是应用幺正变换Uf,使得${U_f}{\kern 1pt} |x\rangle \langle x| \otimes |0\rangle \langle 0| = |x\rangle \langle x| \otimes |f(x)\rangle \langle f(x)|$.
(3) 测量结果.只需要测量辅助位就可以判断函数的奇偶性.根据辅助位的核磁共振谱线向上和向下的谱峰个数的奇偶性来判断函数的奇偶性,即如果向上(或向下)的谱峰个数为偶数(奇数),则映射函数为偶函数(奇函数).同时还要注意一种情况,即当向上和向下的谱线数目相等时,映射函数为偶函数(有些耦合常数较小的核之间的谱线裂分不明显).
2 实验过程与结果根据上面的理论分析,我们实现了两种初态不同的量子算法,一种是以纯态|00〉为初态进行的两量子位的D-J算法;另一种是以混合态为初始态进行的三量子位的Deutsch-like算法.
实验中选择的样品是己炔与仲氢分子发生加成反应后得到的己烯分子,其化学式为

其中核Hb和Hc为加氢化学反应后产生影响的仲氢原子核,其它H均为普通氢原子核.Ha、Hb和Hc之间的耦合常数为,Jbc = 10.5 Hz,Jac = 17.5 Hz.选取Hb和Hc两个核自旋构成的两量子位体系实现量子算法,Hb和Hc化学位移差值为273 Hz.实验是在Bruker 300 MHz型NMR 谱仪上进行的,中心频率对准Hb核.实验中实现4种Uf的脉冲分别为:
${U_{00}}$:不加脉冲
${U_{01}}$:$({\pi \over 2}_{\rm{c}}^{ - y} - ({\pi \over 2})_{\rm{b}}^z - ({\pi \over 2})_{\rm{c}}^z - ({1 \over {2{J_{{\rm{bc}}}}}}) - ({\pi \over 2})_{\rm{c}}^{ - y}$
${U_{10}}$:$({\pi \over 2})_{\rm{c}}^{ - y} - ({\pi \over 2})_{\rm{b}}^{ - z} - ({\pi \over 2})_{\rm{c}}^z - ({1 \over {2{J_{{\rm{bc}}}}}}) - ({\pi \over 2})_{\rm{c}}^y$
${U_{11}}$:$(\pi )_{\rm{c}}^x$
这里${\pi \over 2}$为利用SIMPSON软件得到的选择性优化脉冲,下标表示脉冲对准的核自旋,上标表示脉冲的相位.优化脉冲的脉宽均为1 ms,实验用到的沿z方向的$({\pi \over 2})_{\rm{b}}^z$和$({\pi \over 2})_{\rm{c}}^z$对应的延时时间为930 ms,J耦合演化${1 \over {2{J_{{\rm{bc}}}}}}$对应的实验时间为50 ms.实现以上幺正变化后的实验谱图示于图 2.

|
| 图 2 实现Deutsch-Jozsa算法的NMR谱图. (a)为应用U00后的谱线;(b)为应用U01后的谱线;(c)为应用U10后的谱线;(d)为应用U11后的谱线 Fig. 2 NMR spectra for realizing Deutsch-Jozsa algorithm. (a) Experimental spectra for unitary transformation U00; (b) Experimental spectra for unitary transformation U01; (c) Experimental spectra for unitary transformation U10; (d)Experimental spectra for unitary transformation U11 |
观察图 2中的谱线可知,(a)图和(d)图中Hb核处于正向的吸收形谱峰,Hc核处于负方向的吸收性谱峰,说明U 00和U11是常函数.(c)图和(d)图中Hb和Hc核都处于负方向的吸收形谱峰,说明U01和U10是平衡函数.
上文选择的分子体系通过仲氢诱导极化得到的纯态为两量子位体系,改变体系的初态,分子中的Ha也能应用到量子计算中.以前文介绍的Deutsch-like算法为例,选择自旋Hb为辅助位,自旋Hc和自旋Ha分别作为数据位,经过PASADENA过程后得到的初态为$I_{\rm{b}}^zI_{\rm{c}}^z$.原子核Ha、Hc和Hb按顺序分别定义为量子位1、2和3.实现三量子位Deutsch-like算法的过程如下:
(1) 对初态施加脉冲序列$({\pi \over 2})_{\rm{b}}^y - ({1 \over {2{J_{{\rm{bc}}}}}}) - ({\pi \over 2})_{\rm{b}}^x$得到态$I_{\rm{b}}^z$;
(2) 施加幺正变换Uf,实验中选择了两种幺正变换,分别称其为和,它对应的函数的性质是:函数f1(x)实现的是使输入态$|01\rangle $和$|11\rangle $对应的输出值为1,而其它所有态的输出值为0;函数f2(x)实现的是使输入态$|01\rangle $和$|10\rangle $对应的输出值为1,而其它所有态的输出值为0.函数的矩阵形式分别为:

${U_{{f_1}}}$对应的脉冲变换应该为$({\pi \over 2})_{\rm{b}}^{ - y} - ({1 \over {2{J_{{\rm{bc}}}}}}) - ({\pi \over 2})_{{\rm{bc}}}^y - ({\pi \over 2})_{{\rm{bc}}}^x - ({\pi \over 2})_{{\rm{bc}}}^{ - y} - ({\pi \over 2})_{\rm{b}}^y$:
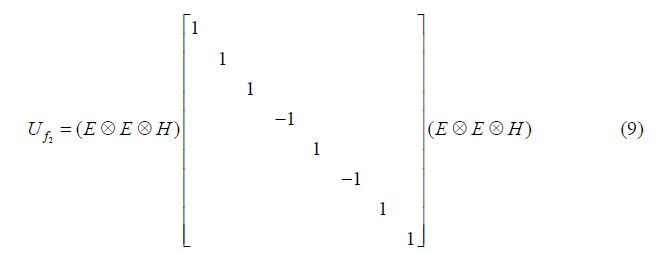
${U_{{f_2}}}$对应的脉冲为:$({\pi \over 2})_{\rm{b}}^{ - y} - (\pi )_{\rm{b}}^z - ({1 \over {2{J_{{\rm{bc}}}}}}) - ({\pi \over 2})_{\rm{c}}^y - ({1 \over {2{J_{{\rm{ca}}}}}}) - ({\pi \over 2})_{\rm{c}}^x - ({\pi \over 2})_{\rm{b}}^z - ({\pi \over 2})_{\rm{b}}^y$.
(3) 测量得出结果,对目标位Hb施加$({\pi \over 2})_{\rm{b}}^y$的脉冲,采样得出谱线.
实验是在安捷伦Varian 700 MHz型NMR谱仪上完成的,目标位为Hb,控制位为Hc,Hb和Hc之间的化学位移差值为637 Hz,Ha和Hc之间的化学位移差值为63 Hz,实验中使用的是高斯型选择性激发脉冲.实施幺正变换后测量自旋Hb得到的谱线如图 3所示.
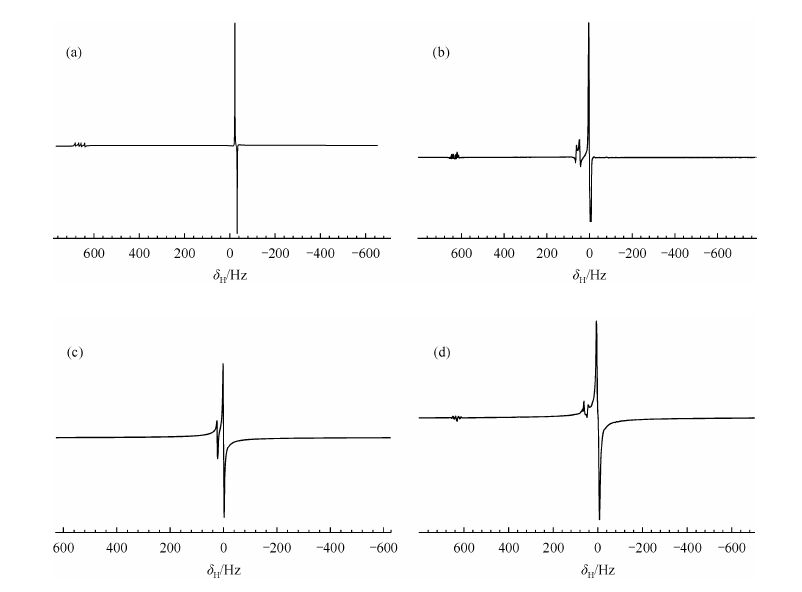
|
| 图 3 实现三量子比特的Deutsch-Like算法的NMR谱图. (a) 实现对应的模拟谱;(b) 实现对应的实验谱;(c) 实现为对应的模拟谱;(d) 实现为对应的实验谱 Fig. 3 NMR spectra for realizing Deutsch-Like algorithm. (a) Simulation spectra corresponding to ; (b) Experimental spectra corresponding to ; (c) Simulation spectra corresponding to ; (d) Experimental spectra corresponding to |
观察谱线可知,此时目标量子比特Hb核的谱线共有两条峰,一条谱峰向上,一条谱峰向下,可以判断对应的函数f1(x)为偶函数,同理对应的函数f2(x)也为偶函数.实验中因为只需对标记位进行观测,即使Ha核没有被极化,也可以充当量子位用于实现量子计算任务.
3 结论本文利用仲氢诱导超极化技术产生的初态实现了两种量子算法,与传统实现量子计算的方法相比,仲氢极化技术能得到直接用于实现量子计算的初态,能避免传统的有效纯态的制备过程,当极化度足够高时得到的态是真正意义上的纯态,能用于实现量子计算中的纠缠过程.同时其信号强度被显著增强,对提高量子计算的有效性,对增强一定的相干时间内实现量子逻辑门的个数具有一定的应用价值.
| [1] | Bowers C R, Weitekamp D P. Transformation of symmetrization order to nuclear-spin magnetization by chemical reactionand nuclear magnetic resonance[J]. Phys Rev Lett, 1986, 57(21): 2 645-2 648 |
| [2] | Natterer J, Bargon J. Parahydrogen induced polarization[J]. Prog Nucl Magn Reson Spectrosc, 1997, 31(4): 293-315. |
| [3] | Duckett S B, Sleigh C J. Applications of the parahydrogen phenomenon: A chemical perspective[J]. Prog Nucl MagnReson Spectrosc, 1999, 34 (1): 71-92. |
| [4] | Duckett S B, Blazina D. The study of inorganic systems by NMR spectroscopy in conjunction with parahydrogen inducedpolarisation[J]. Eur J Inorg Chem, 2003, 2 003(16): 2 901-2 912. |
| [5] | Jones J A. NMR quantum computation[J]. Prog NMR Spectrosc, 2001, 32(29): 325-360. |
| [5] | Jones J A. NMR quantum computation[J]. Prog NMR Spectrosc, 2001, 32(29): 325-360. |
| [6] | Ernst R R, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions[M].Oxford: Oxford Univ Press, 1988. |
| [8] | Chen H W, Lu D W, Chong B, et al. NMR experimental demonstration of probabilistic quantum cloning[J]. Phys Rev Lett,2011, 106(18): 180404. |
| [9] | Chuang I L, Gershenfeld N, Kubinec M. Experimental implementation of fast quantum searching[J]. Phys Rev Lett, 1998,80(215): 3 408-3 411. |
| [10] | Feng G R, Xu G F, Long G L. Experimental realization of nonadiabatic holonomic quantum computation[J]. Phys Rev Lett,2013, 110(19): 190501. |
| [11] | Unruh W G. Maintaining coherence in quantum computers[J]. Phys Rev, 1995, 51(2): 992-997. |
| [12] | Chuang I L, Laflamme R, Shor P, et al. Quantum computers, factoring and decoherence[J]. Science, 1995, 273(5 242):1 633-1 635. |
| [13] | Landauer R. Dissipation and noise immunity in computation and communication[J]. Nature, 1988, 335(6 193): 779-784. |
| [14] | Landauer R. Is quantum mechanics useful[J]. Phil Trans R Soc Lond A, 1995, 353(1 703): 367-376. |
| [15] | Palma G M, Suominen, K A, Ekert A K. Quantum computers and dissipation[J]. Proc R Soc Lond A, 1996, 452(1 946): 567-584. |
| [16] | DiVincenzo D P. The physical implementation of quantum computation[J]. Fort der Physik, 2000, 48(9-11): 771-783. |
| [17] | Feynman R. Simulating physics with computers[J]. Int J Theor Phys, 1982, 21(6-7): 467-488. |
| [18] | Jones J A. NMR quantum computation: A critical evaluation[J]. Fort der Physik, 2000, 48(9-11): 909-924. |
| [19] | Lu Y, Feng G R, Li Y S, et al. Experimental digital quantum simulation of temporal-spatial dynamics of interacting fermionsystem[J]. Science Bulletin, 2015, 60(2): 241-248. |
| [20] | Gershenfeld N A, Chuang I L. Bulk spin-resonance quantum computation[J]. Science, 1997, 275 (5 298): 350-356. |
| [20] | Gershenfeld N A, Chuang I L. Bulk spin-resonance quantum computation[J]. Science, 1997, 275 (5 298): 350-356. |
| [22] | Knill E, Laflamme R, Martinez R, et al. An algorithmic benchmark for quantum information processing[J]. Nature, 2000,404(6 776): 368-370. |
| [23] | Gui L L, Zhou Y F, Jin J Q, et al. Density matrix in quantum mechanics and distinctness of ensembles having the samecompressed density matrix[J]. Found Phys, 2006, 36(4): 1 217-1 243. |
| [24] | Anwar M S, Blazina D, Carteret H A, et al. Implementing Grover’s quantum search on a para-hydrogen based pure stateNMR quantum computer[J]. Chem Phys Lett, 2004, 400(1-3): 94-97. |
| [25] | Deutsch D, Jozsa R. Rapid solution of problems by quantum computation[J]. Proc R Soc Lond A, 1992, 439(1 907): 553-558. |
| [26] | Dorai K, Arvind, Kumar A. Implementation of a Deutsch-like quantum algorithm utilizing entanglement at the two-qubitlevel on an NMR quantum-information processor[J]. Phys Rev A, 2002, 63(3): 034101. |
| [27] | Wei D, Luo J, Sun X, et al. Realization of Deutsch-like algorithm using ensemble computing[J]. Phys Lett A, 2003, 319(3-4): 267-272. |
| [28] | Bowers C R, Weitekamp D P. Transformation of symmetrization order to nuclear-spin magnetization by chemical reactionand nuclear magnetic resonance[J]. Phys Rev Lett, 1986, 57(21): 2 645-2 648. |
| [29] | Koch A, Ulrich C, Bargon J. In situ NMR observation of tin trichloride-activated rhodium dihydride complexes usingparahydrogen induced polarization[J]. Tetrahedron, 2000, 56(20): 3 177-3 179. |
| [30] | Deutsch D, Jozsa R. Rapid solution of problems by quantum computation[J]. Proc R Soc Lond A, 1992, 439(1 907): 553-558. |
| [31] | Cleve R, Ekert A, Macchiavello C, et al. Quantum algorithm revisited[J]. Proc R Soc Lon A, 1998, 454(1 960): 339-354.第4 期 62田佳欣等:利用仲氢诱导极化技术实现Deutsch算法 7 |
| [32] | Wei D X, Yang X D, Luo J, et al. NMR experimental implementation of three-parties quantum superdense coding[J].Chinese Sci Bull, 2004, 49(5): 423-426. |
 2015, Vol. 32
2015, Vol. 32




