波谱学杂志  2015, Vol. 32 Issue (4): 563-573

文章信息

胡 浩, 韦芝良, 林良杰, 孙惠军, 林雁勤, 陈 忠
HU Hao, WEI Zhi-liang,LIN Liang-jie, SUN Hui-jun, LIN Yan-qin, CHEN Zhong
基于选择编码的超快速磁共振波谱
A Selective Encoding Method for Ultrafast Magnetic
波谱学杂志, 2015, 32(4): 563-573
Chinese Journal of Magnetic Resonance, 2015, 32(4): 563-573
http://dx.doi.org/10.11938/cjmr20150402

文章历史

收稿日期：2015-02-11
收修改稿日期：2015-10-25
 Abstract              PDF               Figures               Tables
引用本文 0
胡 浩, 韦芝良, 林良杰, 孙惠军, 林雁勤, 陈 忠. 基于选择编码的超快速磁共振波谱[J]. 波谱学杂志, 2015, 32(4): 563-573.
HU Hao, WEI Zhi-liang,LIN Liang-jie, SUN Hui-jun, LIN Yan-qin, CHEN Zhong. A Selective Encoding Method for Ultrafast Magnetic[J]. Chinese Journal of Magnetic Resonance, 2015, 32(4): 563-573.
基于选择编码的超快速磁共振波谱
胡 浩, 韦芝良, 林良杰, 孙惠军, 林雁勤, 陈 忠    
厦门大学 电子科学系，福建省等离子体与磁共振研究重点实验室，福建 厦门 361005
收稿日期：2015-02-11；收修改稿日期：2015-10-25
基金项目:国家自然科学基金资助项目(11105114, 11475142)，福建省自然科学基金资助项目(2014J05012)．
作者简介: 胡浩(1987-)，男，湖北武穴人，硕士研究生，主要从事核磁共振研究．
*通讯联系人：林雁勤，电话：0592-2183301, E-mail: linyq@xmu.edu.cn；韦芝良，电话：0592-2181712, E-mail: zyliamwei@gmail.com.
摘要：核磁共振(NMR)波谱技术是当今最有力的谱学工具之一，在化学、生物和医药等众多领域获得重要而广泛的应用．基于时空编码的快速采样方法自2002年Frydman小组提出后，大大增强了高维磁共振波谱的采样效率．在某一些应用体系中，存在若干个强度远超于其他谱峰的情况，很容易由于动态增益不足而检测不到某些较弱的谱峰，而往往这些较弱的谱峰包含着感兴趣的信息．且在实际的化学生物应用中，存在选择性感兴趣检测的情况，即只需要选择性地观察若干个具有标记作用的谱峰．由于时空编码技术借助于高速切换的双极性梯度来完成解码，因而无法选择性地检测若干个非连续的频点．为解决以上两个问题，该文提出一种选择编码的时空编码方法，即在序列中施加选择性脉冲，选择性破坏某些谱峰的编码过程，使之不能在解码期解码，从而简化谱图，实现选择性压制或者非连续频点的感兴趣检测．如果把选择性反转脉冲换为硬反转脉冲加选择性反转脉冲，则最终的谱图中只出现被选择性脉冲选中的谱峰．理论分析及相关的实验验证了这种方法的可行性和有效性．
关键词： 核磁共振(NMR)     选择编码     二维核磁共振谱     空间编码     超快速    
A Selective Encoding Method for Ultrafast Magnetic
HU Hao, WEI Zhi-liang , LIN Liang-jie, SUN Hui-jun, LIN Yan-qin , CHEN Zhong    
Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China
* Corresponding author: LIN Yan-qin, Tel: +86-592-2183301, E-mail: linyq@xmu.edu.cn; WEI Zhi-liang, Tel: +86-592-2181712, E-mail: zyliamwei@gmail.com.
Abstract: Nuclear Magnetic Resonance (NMR) is one of the most powerful analytical tools nowadays, with wide applications in the fields of chemistry, biology and medicine. The spatial encoding ultrafast method proposed by Frydman et al. in 2002 greatly enhanced the sampling efficiency of multi-dimensional NMR spectroscopy. One problem with the Frydman’s method is that it is difficult to selectively detect multiple resonances at non-continuous discrete frequencies, due to the fast-switching bipolar gradients that are required for spatial encoding. In this study, we proposed a novel selective spatial encoding ultrafast method, aiming to solve two problems often encountered when utilizing the Frydman’s method in practical chemical and biological applications. The first problem is to detect weak signals in the presence of strong signals with limited dynamic range; and the second problem is to detect the signals of interests (e.g., peaks from labeled nuclei) exclusively with the rest of resonances in the background unexcited. The proposed method utilized a selective pulse to destroy the encoding process selectively, such that selective suppression of strong peaks or excitation of non-continuous discrete frequency points of interest could be achieved. We also showed that only the spectral peak selected by the selective pulse would remain if the selective inverse pulse was replaced by a hard inverse pulse. The feasibility and validity of this method were demonstrated by both theoretical analyses and experiments.
Key words: nuclear magnetic resonance (NMR)     selective encoding     two-dimensional NMR spectrum     spatial encoding     ultrafast    
引言

核磁共振(Nuclear Magnetic Resonance，NMR)技术是一种在分子水平上解析物质结构的有效手段[1, 2]，在现代科学研究中有着不可替代的作用．尤其是，二维(2D) NMR波谱技术的提出与发展极大地拓展了NMR技术的研究和应用领域[6]．2D NMR波谱的最大吸引力在于大大提高了NMR技术分离复杂信号的能力，减少相邻谱峰之间的重叠，而且能够提供很多一维(1D) NMR谱无法提供的结构信息，如互相重叠的共振信号中每一组信号的精细裂分形态、准确的耦合常数、耦合常数的符号以及直接和远程耦合信息等．常规2D NMR通过加入一个时间递增的自由演化量，对FID数据进行傅里叶变换，得到二维谱图．由于每次采样之前都有等待时间（用于恢复纵向磁化矢量），且为保证一定的分辨率和信噪比需要大量的扫描，所以常规2D NMR波谱的采集需要较长时间．因此，自2D NMR提出以来，如何加速其采样过程就成为了人们探讨的热点问题．尤其是在蛋白质研究中提出了高维NMR波谱的概念以后，讨论此问题更是达到了空前的热度．

很多研究人员提出了不少加速的解决办法．法国的Schanda和Brutscher使用的小角度激发[7, 8]就是其中一种方法，它能够在较短的时间内获得蛋白质样品的二维谱．它是通过优化激发射频脉冲的角度使得等待时间变短，从而节约大量的采样时间．但是小角度没有最大程度地激发磁化矢量而使谱图信噪比较低，为解决这一问题，基于回波链采样的序列应用而生[9, 10]．通过不断地施加混合期与采样，在单次扫描中，同时采集到多个信号，再通过数据处理，获取高信噪比的NMR谱．实际中，很多物质的NMR波谱都具有一定的稀疏性．鉴于此，英国的Freeman等人[11]提出了基于频域直接构建2D NMR谱的方法．通过使用多频点激发的选择性脉冲和哈达玛(Hadamard)矩阵编码，只采集到少数感兴趣谱峰的谱线，再利用同一哈达玛矩阵进行解码，提取出每一条谱线，从而重建出2D NMR谱．此外，对角化滤波方法[12, 13]通过对时域信号做匹配，直接获得频点信息，只从少量的数据中就可以重构出分辨率很好的谱图，为节约采样时间提供了一种有益的思路．传统的采样方式都是均匀采样，受到奈奎斯特定律的制约．因此，研究人员提出了许多非等间隔采样的技术．2002年，Frydman小组提出了基于时空编码的单扫描快速采样技术[14]，它是所有加速技术中最有吸引力的一种．因为这种技术以空间编码代替传统的时域编码，借助于平面回波谱成像[15]采样模块，在单次扫描中就可以获取2D NMR谱，并且时空编码的概念可以向更 高维度拓展，具有很强的加速能力．在早期的时空编码技术中，编码是通过一系列中心漂移的软脉冲配合梯度来完成的，即离散编码，这种方法对硬件要求较高，同时实验呈现出很强的参数敏感性，容易出现“鬼峰”、分辨率不足等问题[16]．法国的Pelupessy于2003年提出利用具有扫频激发特性的绝热chirp脉冲代替离散编码[20]，实现了连续编码，从而提高了编码效率，解决了以上问题．在时空编码技术提出后的十余年间，许多的科研工作者对这项技术的各项细节进一步完善，从而使这项技术具有很强的应用价值[21]．

本文就是使用基于时空编码的单扫描快速采样技术得到相关谱[22] (Correlation Spectroscopy,COSY)来完成我们的实验．相关谱是2D NMR技术中最常见、实用的一种．传统的COSY有以下两个方面的缺点：1) 不能针对感兴趣区域进行检测，即不能只采出几个感兴趣谱峰的耦合结构，必须采集整张谱；这个主要原因在于COSY是基于傅里叶变换的．2) 当谱图中同时出现几个强度具有绝对优势的谱峰时，受限于接收机的动态范围，会损失某一些强度比较弱的谱峰；当只有个别这种强峰时，通过压制就能取得很好的结果，但如果同时出现非连续的若干个峰时，压制技术很难同时取得很好的压制效果．下面我们介绍一种基于选择编码的超快速时空编码方法．它是受时空编码单扫描技术及多频点激发选择性脉冲启发，把这两种思想结合起来产生的．它基于时空编码，因而具有超快速方法单次扫描完成二维谱采集的天然特性；它利用选择编码的思想，通过在一定的位置施加选择性脉冲，从而影响编码过程，可以根据需要同时激发或者去除某几个连续或非连续的谱峰，以有利于观测感兴趣区域，从而更好的解析所关注的谱峰信息．

1 理论部分 1.1 空间编码超快速方法

常规2D NMR实验的脉冲序列一般分为预备期、演化期、混合期、采样期．空间编码单扫描超快速方法同样包含以上4个部分，不同的是演化期是通过空间编码的方式来代替常规二维谱间接维编码，而采样期通过解码的方式来代替常规的采样，最终达到只需采样一次就可以获得二维谱数据的目的．常规二维谱需等间隔增加t1增量并连续执行N1次实验，而空间编码方法是将样品按空间分成独立的N1份，每份样品经历不同的演化时间，这样一次采样得到的数据就含有不同的t1，经过数据处理后就可以得到完整的二维谱数据，采集时间只需几百毫秒．

1.2 多色组合软脉冲

以标准的Gauss脉冲为基础，进行多次的相位调制，能够获得可选择性激发多个频点的脉冲，我们把它称为多色组合软脉冲[1]．它在实现多频点同时激发的同时，还保留了相位信息的连续性．它不仅可以实现多个频点的同时激发，也可以根据需要改变被激发频率点的相位．多频点选择结合时空编码技术可以同时控制多个频点的编码过程，从而实现感兴趣非连续频点的检测．选择性编码的超快速方法不仅具有时间优势，还可以为实际研究需要，选择感兴趣频点，分析其详细的局部信息．

1.3 新序列图及算符推导

在本文的实验中，我们用到了两种脉冲序列，如图 1所示．图中RF表示射频脉冲，Gz表示Z方向的梯度脉冲，空心矩形表示硬脉冲，带有箭头的圆顶图标表示绝热chirp脉冲，sinc形状脉冲表示选择性软脉冲，各个脉冲上都标有名字．第一个方框[]内表示编码模块，NE表示编码次数，第二个方框[]内表示解码模块，ND表示解码次数．其中图 1(a)是横向选择性编码超快速实验序列，在编码期正反梯度编码之间加入一个选择性脉冲，从而对横向磁化矢量进行调制，影响其编码过程．为方便表述，I表示被选择性脉冲选择到的核，S代表未被选择的核，假设NE = 1．首先我们施加一个p / 2硬脉冲使纵向磁化矢量翻转到水平面，然后通过选择编码模块对样品进行编码．I核的量子阶依次为：-1→+1→-1→+1→-1，S核的量子阶依次为+1→-1→+1→-1．由于采用的是基于相位调制的恒时时空编码，标量偶合对空间编码没有影响，在以下的分析中省略（具体见文献[2]）．第一个chirp脉冲后，S核累加的相位为：

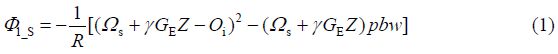
图 1 (a) 横向选择性编码序列，(b) 纵向选择性编码序列 Fig. 1 (a) Pulse sequences with transverse selective encoding,(b) and longitudinal selective encoding
图选项

(1)式中：R为chirp脉冲的扫频速率，Ws为S核的化学位移，g 为旋磁比，Oi为chirp脉冲激发的起始频率，pbw为chirp脉冲的扫频宽度，GE为编码梯度大小．因为S核未被选择到，所以经历选择性反转脉冲后，相位没有改变．第二个chirp脉冲后，S核累加的相位为：

(2)式中：Ootr为chirp激发中心频率．第二个p/2硬脉冲对相位没有影响，图 1中GP梯度作用是对谱峰位置的调节，也跟相位无关．设从某一解码梯度的起始到采样时刻的时间为ta，那么

当NE不为1时，

对于选择到的I核，对应的相位变化依次如下：

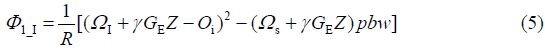
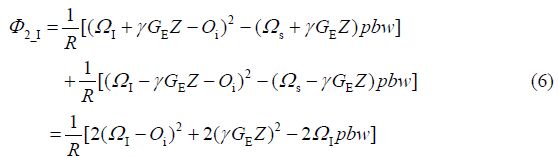
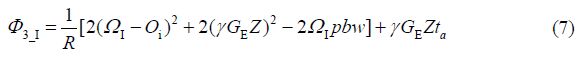
空间编码的过程可以理解为把化学位移与空间位置相关联起来，即在数学模型中出现项．这一项在解码期经历反复的解缠绕与缠绕就可以获得化学位移信息．从上述公式中可以看出I核最后相位中没有项，而S核最后相位中有项，所以在最终的谱图中我们看不到被选择性反转的谱峰信息．如果把这里的选择性反转脉冲换成多色脉冲，则可以同时过滤多个共振峰的信息．如果把选择性反转脉冲换为硬反转脉冲加选择性反转脉冲，则最终的谱图中只出现被选择性脉冲选中的谱峰．

选择性脉冲的脉冲宽度与选择频带成反比，如果需要很精确地选择某一频带，则需要很长的脉冲宽度．在编码期中间施加长时间的选择性脉冲可能会带来严重的横向弛豫衰减，降低信号的信噪比．另一方面，虽然标量偶合不能被恒时时空编码所编码，却可以通过编码期的总时长来影响最终二维谱中对角峰与交叉峰的强度比例．在编码期施加软脉冲相当于延长了编码期的时长，最终获得的二维谱存在检测不到某一些峰的风险．基于以上两个方面的原因，如图 1(b)的纵向选择性编码超快速实验序列可以作为选择方案．在纵向选择性编码中，选择性脉冲被置于序列开始前（虚框表示选择性软脉冲可选）．这种实验需要扫描两次，一次在p/2硬脉冲之前加入选择软脉冲，另外一次不加软脉冲．施加选择软脉冲的一次扫描由于被选择的谱峰都经历了纵向磁化矢量反转，与未施加的一次实验结果相加则相消．由于仅对纵向磁化矢量进行操作，避免了横向弛豫的影响；且不影响编码期的长度，为获取更好的二维谱峰强度比例留下调节空间．纵向选择性编码会受纵向弛豫的影响，然而液态磁共振实验样品的纵向弛豫时间一般比横向弛豫时间长得多，受纵向弛豫影响较小．因此特别对于短T2的样品，纵向选择性编码超快速实验序列要优于横向选择性编码超快速实验序列．

2 结果与讨论 2.1 仪器及试剂

所有的实验都是在安捷伦公司Varian 500 MHz型NMR谱仪上完成．该谱仪配备5 mm间接检测探头及三维脉冲梯度场．为了展示方法的可行性与基本原理，一部分实验是以混合溶液（三溴丙酸乙酯与丁酮以1∶1比例混合）为样品完成的；为了证明方法的有效性及应用潜力，我们还选择玉米油为样品进行了另一部分的实验．

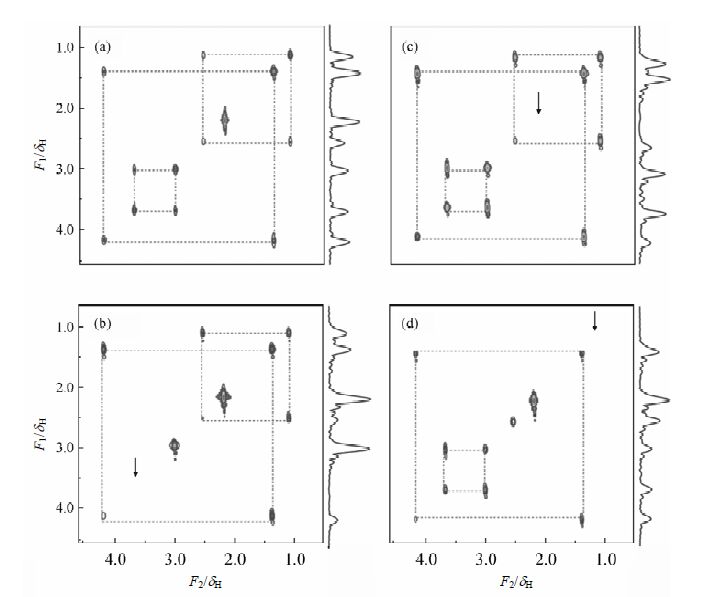
2.2 混合溶液实验

本实验中我们使用三溴丙酸乙酯与丁酮的1∶1混合溶液来验证上面的序列．主要实验参数为：编码梯度GE = 2.93×10-4 T/cm，解码梯度GD= 39.07×10-4 T/cm，GP = -5.86 ×10-4 T/cm，GP作用时间tP= 0.001 s，chirp脉冲时间t = 0.01 s，选择性软脉冲宽度为10 ms，直接维采样时间间隔TD = 250 ms，直接维采样点数ND = 400，谱宽SW = 500 kHz．图 2(a)所示为未加选择激发软脉冲的完整空间编码2D COSY谱图．由图 2(a)可知，混合溶液的COSY谱中存在3组耦合，分别是d1.02与2.50、d1.30与4.19和 d2.98与3.69（未给出对称的交叉峰）．图 2(b)~(d)图是使用横向选择性编码方法分别选择激发3个位置的谱峰（分别是d 3.69、2.13和1.02）得到的2D COSY谱图．3张图中标箭头处表示在图 2(a)中有而经过选择性编码后不再出现的谱峰．这些被选择的谱峰不再出现在所对应的二维谱中，不仅对角峰不再出现，而且对应的交叉峰也消失了．为进一步确认选择性编码的效果，图 2(a)~(d)分别给出了F1维的投影谱．从投影谱中可以看出，被选择到的频点不再出现谱峰．综合选择性编码二维谱及投影谱的结果，可知选择性编码可以选择性地去除某个谱峰．

图 2 (a) 三溴丙酸乙酯二维空间编码COSY谱图，(b)~(d)分别是横向选择编码激发某个谱峰后二维空间编码COSY谱图 Fig. 2 (a) Ethyl 3-bromopropionate 2D spatial encoding COSY spectrum,(b)~(d) 2D spatial encoding COSY spectra after transverse selective excitation of certain spectral peak,as indicated by arrow
图选项

图 3(b)~(d)中是使用纵向选择性编码超快速实验序列分别选择激发3个位置的谱峰（分别是d 3.69、2.13和1.02）得到的二维空间编码COSY谱图．从图中可以看到，纵向选择性编码达到横向选择性编码类似的效果，即被选择的谱峰位置不再出现对角峰或者交叉峰．对比图 3和图 2(b)~(d)的三图的间接维投影一维谱图可以看到，纵向选择编码间接维比横向选择编码的投影谱效果更好，裂分更清晰，峰强度有提高．

图 3 (a) 三溴丙酸乙酯二维空间编码COSY谱图，(b)~(d)分别是纵向选择编码激发某个谱峰的二维空间编码COSY谱图 Fig. 3 (a) Ethyl 3-bromopropionate 2D spatial encoding COSY spectrum,(b)~(d) 2D spatial encoding COSY spectra after longitudinal selective excitation of certain spectral peak,as indicated by arrow
图选项

图 2和图 3都是单个谱峰的选择性激发．如果把对应的单频点选择性脉冲换为多色脉冲，则可以实现多个频点的选择性激发．由于可以自由地设置多色脉冲的频点，因此可以非连续地选择几个频点．如图 4(a)结果所示，对三溴丙酸乙酯使用横向选择编码序列，多色脉冲分别选择了d1.02、2.13和2.50三个频点，最终这3个频点不再出现，只留下d1.30与4.19和d2.98与3.69两对耦合．此时，如果在多色脉冲前施加一个硬脉冲，就可以起到反选的效果，如图 4(b)，只留下d2.13处的单峰和d1.02与2.50一对偶合．由于时空编码技术的特殊编解码机理，间接维的信号呈现一定的sinc尾波，容易影响邻近峰的判别．虽然加一些窗函数能起到一定的改善作用，但并不能 从根本上解决问题．此处所采用的选择性编码技术，既可以选择只留下感兴趣的某几个非连续的谱峰，也可以把某一引起谱图强度差异大的谱峰分成两组，分别采集谱图，以避免相互影响．这就相当于以另一种形式增加了谱宽，或者说在有限谱宽里得到了更清楚的信息．

图 4 同时横向选择激发几个谱峰后的三溴丙酸乙酯二维空间编码COSY谱图 Fig. 4 Ethyl 3-bromopropionate 2D spatial encoding COSY spectra after transverse selective excitation of several spectral peaksy
图选项
2.3 玉米油实验

玉米油是一种生活中常见的一种脂类，由于很多生理医学中的疾病都需要对脂类进行检测，本文中，我们选择玉米油来验证选择性编码在脂类研究中潜在的应用价值．

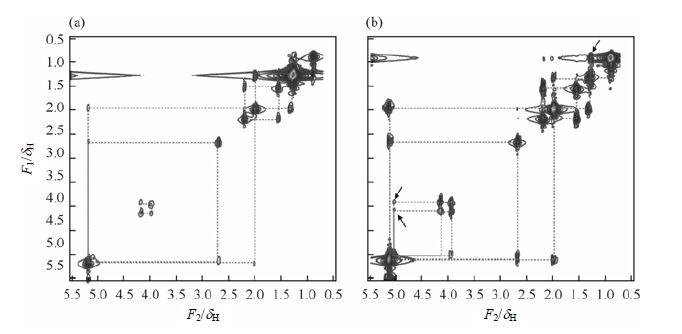
主要实验参数为：编码梯度GE = 2.93×10-4 T/cm，解码梯度GD= 39.07×10-4 T/cm，GP= 5.86×10-4 T/cm，GP作用时间tP= 350 ms，chirp脉冲时间t = 0.01 s，选择性软脉冲宽度为15 ms，直接维采样时间间隔TD = 200 ms，直接维采样点数ND = 400，谱宽SW = 500 kHz．玉米油的一维谱中，共包含以下谱峰：d0.85、1.25、1.56、2.01、2.21、2.72、4.04、4.25、5.18和5.28．其中d 1.25处的谱峰强度远高于其它峰，导致其他对角峰之间交叉峰信息不容易被检测到．如图 5(a)所示，由于d 1.25处的强峰影响，在d1.25处附近的偶合判断受到影响，且位于d 5.37处的交叉峰也不容易被检测．此时，利用选择性编码方法得到如图 5(b)的结果．从图中可以看出，由于d 1.25处的峰受到选择性编码的作用，强度受到极大的衰减，附近的偶合结构变得很清晰，且远处的耦合结果也能被检测到．如图所示，图 5(a)中可以看到5对耦合：d 5.28与2.72、d 5.28与2.01、d 4.25与4.04、d 2.21与1.56、d 2.01与1.25，图 5(b)中可以看出新增了3对耦合：d 5.18与4.25、d 5.18与4.04、d 1.25与0.85，如图中箭头所示．

图 5 (a) 玉米油二维空间编码COSY谱，(b) 横向选择编码后的玉米油二维空间编码COSY谱 Fig. 5 (a) 2D spatial encoding COSY spectrum of corn oil,(b) 2D spatial encoding COSY spectrum of corn oil after transverse selective encoding
图选项
2.4 与Hadamard方法的比较

从前面的实验结果可知，选择编码方法可以很好的实现同时选择几个频点的谱峰．Hadamard方法也是可以实现选择激发的．但是Hadamard方法通常需要多通道独立扫描才能解码，且Hadamard矩阵的阶数通常要等于或大于实验中的通道数目．对比之下，上面的横向选择性超快速实验方法只要单扫描，纵向选择性超快速实验方法也只要两次扫描，编解码简单，效果也比较好．所以本文的结果比Hadamard方法要简单易操作．

3 结论

在本文中，我们发展了基于选择编码超快速磁共振波谱学方法，可以用来选择压制较强的谱峰或者去掉干扰峰，或者反选留下想要关注的谱峰．在实际应用中，可以根据谱峰的频率参数生成合适的选择软脉冲，准确的激发对应的谱峰．在代谢组学中，经常要分析某些结构或者某些官能团的谱图信息，往往这些样品的谱图很复杂，为了达到分析的目的，需要对感兴趣的谱峰选择出来作重点分析．本文中的方法就可以应用到代谢组学中，实现这一选择性分析的目的．

参考文献
[1] Du Tian-peng(杜天鹏), Zhang Zi-wei(张子微), Zeng Dan-yun(曾丹云), et al. Structure and function of influenza virusfusion peptide studied by nuclear magnetic resonance spectroscopy(流感病毒融合肽磁共振研究进展)[J]. Chinese JMagn Reson(波谱学杂志), 2014, 31(4): 596-607.
[2] Wang Zhi-zhan(王志战), Qin Li-ming(秦黎明), Gai Shan-shan(盖姗姗), et al. The effects of oil-mixed drilling fluid on oillayer identification studied by NMR spectroscopy(利用NMR 技术判识混油钻井液条件下钻遇的油层)[J]. Chinese JMagn Reson(波谱学杂志), 2014, 31(4): 579-586.
[3] Bain A D, Bornais J, Brownstein S. Analysis of generalized two-dimensional homonuclear NMR-spectra[J]. Can J Chem,1981, 59(4): 723-730.
[4] Linder M, Hohener A, Ernst R R. Orientation of tensorial interactions determined from 2-dimensional NMR powderspectra[J]. J Chem Phys, 1980, 73(10): 4 959-4 970.
[5] Aue W P, Bartholdi E, Ernst R R. Two-dimensional NMR spectroscopy. Application to nuclear magnetic resonance [J]. JChem Phys, 1976, 64(5): 2 229-2 246.
[6] Schanda P, Brutscher B. Very fast two-dimensional NMR spectroscopy for real-time investigation of dynamic events inproteins on the time scale of seconds[J]. J Am Chem Soc, 2005, 127(22): 8 014-8 015.
[7] Nolis P, Perez-Trujillo M, Parella T. Multiple FID acquisition of complementary HMBC data[J]. Angew Chem Int Ed, 2007,46(39):7 495-7 497.
[8] Frydman L, Gal M. Single-scan 2D NMR correlations by multiple coherence transers[J]. J Magn Reson, 2010, 203(2): 311-315.
[9] Kupce E, Freeman R. Frequency-domain hadamard spectroscopy[J]. J Magn Reson, 2003, 162(1): 158-165.
[10] Kupce E, Freeman R. Two-dimensional hadamard spectroscopy[J]. J Magn Reson, 2003, 162(2): 300-310.
[11] Mandelshtam V A. FDM: The filter diagonalization method for data processing in NMR experiments[J]. Prog Nucl MagnReson Spectrosc, 2001, 38(2): 159-196.
[12] Frydman L, Lupulescu A, Scherf T. Principles and features of single-scan two-dimensional NMR spectroscopy[J]. J AmChem Soc, 2003, 125(30): 9 204-9 217.
[13] Frydman L, Scherf T, Lupulescu A. The acquisition of multidimensional NMR spectra within a single scan[J]. Proc NatlAcad Sci USA, 2002, 99(25): 15 858-15 862.
[14] Mansfield P. Spatial mapping of the chemical shift in NMR[J]. Magn Reson Med, 1984, 1(3): 370-386.
[15] Shrot Y, Frydman L. Ghost-peak suppression in ultrafast two-dimensional NMR spectroscopy[J]. J Magn Reson, 2003,164(2): 351-357.
[16] Pelupessy P. Adiabatic single scan two-dimensional NMR spectroscopy[J]. J Am Chem Soc, 2003, 125(40): 12 345-12 350.
[17] Zhang Z Y, Chen H, Wu C, et al. Spatially encoding ultrafast high-resolution 2D homonuclear correlation spectroscopy ininhomogeneous fields[J]. J Magn Reson, 2013, 227: 39-45.
[18] Zhao Ming-fang(赵明芳), Wu Can(吴灿), Lin Yu-lan(林玉兰), et al. Single-scan ultrafast methods and their applicationsin NMR[J]. Chinese J Magn Reson(波谱学杂志), 2009, 26(4): 541-559.
[19] Wei Z L, Yang J, Lin L J, et al. Reverse detection for spectral width improvements in spatially encoded dimensions ofultrafast two-dimensional NMR spectra[J]. Magn Reson Chem, 2014, 52(11): 680-685.
[20] Thomas M A, Yue K, Binesh N, et al. Localized two-dimensional shift correlated MR spectroscopy of human brain[J].Magn Reson Med, 2001, 46(1): 58-67.
[21] Kupce E, Freeman R. Polychromatic selective pulses[J]. Prog Nucl Magn Reson Spectrosc, 1993, 102(1): 122-126.
[22] Wei Z L, Lin L J, Lin Y Q, et al. Ultrafast acquisition of localized two-dimensional magnetic resonance correlated spectraof inhomogeneous biological tissues with resolution improvements[J]. Chem Phys Lett, 2013, 581: 96-102.