文章信息
- 韩明月,郑慧,胡炳文, 杨光
- HAN Ming-yue, ZHENG Hui, HU Bing-wen, YANG Guang
- 迭代软阈值法压缩感知重建谱峰较宽的二维固体谱
- Compressed Sensing Reconstruction with Iterative Soft Thresholding for Two-Dimensional Solid-State NMR Spectra with Broad Peaks
- 波谱学杂志, 2015, 32(4): 551-562
- Chinese Journal of Magnetic Resonance, 2015, 32(4): 551-562
- http://dx.doi.org/10.11938/cjmr20150401
-
文章历史
- 收稿日期:2014-11-24
- 收修改稿日期:2015-10-24
核磁共振(NMR)由于在结构分析方面的特殊优势,其理论和技术得到了迅速的发展.而固体核磁共振可以用来研究无法溶解的固体样本以及固体状态下的结构信息,因此在物理、化学、材料和矿物等方面的得到了广泛的应用[1].傅里叶变换二维谱技术为固体核磁共振奠定了基础[2].二维核磁共振谱采集具有两个独立时间变量的信号,并经二维傅里叶变换得到具有两个独立频率变量的谱图.一般用第二个时间变量t2表示采样时间,第一个时间变量t1 则表示脉冲序列中的某一个变化的时间间隔.对于每个t1间隔在检测期t2采集一个单独的FID,得到N1个FID信号,这样获得两个时间变量的谱函数< b>S (t1,t2),然后进行二维傅里叶变换得到频率域的二维谱S (F1,F2).
核磁共振波谱的时域数据采集时间有时可以长达几天,因此通过欠采样时域数据来减少采样时间,并利用特定的重建方法得到良好的图谱是核磁共振领域的一个重要课题[3].对于核磁共振二维谱的重建已有一些传统的方法,如协方差法(Covariance)[4]、最大熵法(Maximum Entropy,MaxEnt)[5]、不均匀傅里叶变换法[6]等,这些算法根据不同类型的图谱的特点,提出不同的假设,给出适合的解决方案.而最近提出的压缩感知(Compressed Sensing,CS)技术可以打破奈奎斯特采样定律的限制,对欠采数据采用压缩感知技术进行重建,仍然能较好地重建信号[7].
在信号和图像重建领域,常常需要对采集的数据进行重建.当信息采集的过程是线性时,那么问题就转化为线性方程组求解的问题[8].当观测值$y \in {C^M}$,以及其对应的变换域信号为$x \in {C^N}$.

矩阵$\Psi \in {C^{M \times N}}$是采样矩阵,即对应于信号采集的线性变换.传统的方法要求观测数据ψ的个数M要至少等于信号x 的长度N才能重建出信号.如果M< N,则意味着此线性系统是欠定的,可能的解有无数种.在没有额外信息的情况下,不可能在M< N的情况下从观测值ψ中恢复信号x [9].然而压缩感知理论提出,在信号满足稀疏性假设的情况下,能重建出信号.所谓稀疏性,指的是信号本身或者信号在某个变换域中只在有限的点上取得非0值[10].由于现实世界中的大部分信号都是可压缩的,因此他们在某种意义上也都是稀疏的.核磁共振波谱在频率域的峰是相对孤立的,有意义的谱峰个数与噪声数据个数相比较很少,并且有意义的谱峰系数都很大,特别是双量子-单量子(DQ-SQ)谱和魔角旋转下的多量子谱(MQMAS)本身就有很高的稀疏性,符合压缩感知领域稀疏性的要求[11].本文对于谱图的迭代重建过程将频域直接作为稀疏域.压缩感知的另一个要求是,测量域与稀疏域之间不能具有相关性,由于两维谱的测量在时间域进行,与频域之间具有较好的非相关性.所以核磁共振二维谱非常适合于压缩感知技术相结合.
欠采时域数据可以加速采集,然而当采样率较低时,又会导致某些伪信号的出现或者真实谱峰的变弱甚至消失[12].我们先前的研究结果发现,基于共轭梯度方法的压缩感知技术在重建谱峰较窄的固体DQ-SQ二维固体方面谱(如13C DQ-SQ,29Si DQ-SQ)方面效果显著,尤其是当谱峰较窄且相距较远时,能够完美重建.然而当应用共轭梯度方法重建谱峰较宽的一类谱图时,效果却不尽人意.本文拟采用软阈值方法重建固体1H DQ-SQ二维NMR谱图和MQMAS NMR谱图.在欠采时域空间数据的条件下,不仅降低了噪声,而且保证重建效果,解决了宽峰难以重建的问题.本文的总体结构分为3个部分:第一部分是压缩感知与软阈值方法的理论介绍,第二部分是软阈值方法应用于稀疏域重建的实验结果,以及软阈值方法与共轭梯度方法在采样率相同的情况下实验结果的比较分析,第三部分为实验结论总结部分.
1 基本理论 1.1 压缩感知原理寻找线性方程的欠定系统的稀疏解,是解决许多现实情况中都会遇到的问题,例如信号和图像处理、压缩以及统计相干等方面.而解决稀疏信号重建的问题,Candes E J、Romberg J K、Tao T和Donoho D L提出的压缩感知理论引起了许多研究者的兴趣[21, 22].
$x \in {R^N}$是未知信号,$y \in {R^M}$是用矩阵φ对未知信号进行观测得到的结果.若M=N,即φ为方阵,且φ中每列相互正交,则未知信号x 可由测量结果ψ唯一确定.若M< N,该问题变成欠定方程求解问题,一个ψ对应无穷多个解x .若未知信号x 是稀疏的或未知信号在某变换域Y 中稀疏,即$||x|{|_0} = K < < N$或$x = \Psi \alpha $,,则该欠定方程的求解变成如下优化问题:
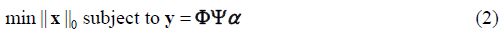
虽然利用l0范数的最小化可以找到最稀疏的解,但l0范数的最小化却是一个NP-hard (Non-deterministic Polynomial hard)问题,无法在合理的时间内找到问题的解.因此将解决l0范数问题可以修改为解决l1范数问题:
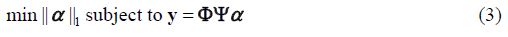
(3)式可以等价于下面的形式:

(4)式中l是规划参数,用来平衡数据的连续性和稀疏性.l1范数的优点在于,基于它的算法运算相对简单并且速度较快.
1.2 迭代软阈值方法(Iterative Soft Thresholding,IST)阈值迭代算法在信号处理领域的应用方面有很长的历史,它的思路简单且容易实现[19],也被用在磁共振成像领域中[21, 22].最早出现的硬阈值方法在每次迭代的过程中,将信号与全局阈值l比较,高于阈值的信号数值保持不变,而低于阈值的信号则置0[20].本文采用的软阈值算法,其对高于阈值的信号不是保持不变而是进行适当的收缩[21, 22].当用软阈值进行阈值操作,对某一点进行阈值迭代直到该点的值趋于固定的值,Donoho D L提出这等同于重建过程最小化l1范数[23, 24].下式为我们采用的阈值收缩方法:
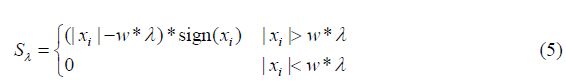
x表示稀疏域的数据如谱图数据,l是使用的阈值,该阈值不是一个固定数值,而是会根据数据进行调整[25].在最优化的文献中,软阈值迭代算法可以追溯到邻近前向后向迭代算法(Proximal Forward-backward Iterative Scheme)[26, 27]和一般的分裂算法(Splitting Methods)[28].l可以设置为稀疏域的最大模值的1%,从而达到自适应调节阈值的目的.
在迭代的过程中,分为两个过程:时域数据保真过程和稀疏域数据的阈值收缩过程.即下式:

其中b为欠采的时域数据,${\Psi _u}$为欠采样反傅里叶变换,即变密度随机采样矩阵与反傅里叶变换操作相结合,${\Psi ^{ - 1}}$表示傅里叶变换,${x^{[n]}}$表示第次重建的谱图,表示第n+1次重建的稀疏域谱图.
1.3 伪随机采样模式压缩感知技术要求伪影噪音满足非相干性,即时域数据欠采导致在重建过程中产生的噪音是非相干的[29].Nayak K S等人[30]提出的随机采样模式能够消除伪影相干性.在随机采样的思想下使用幂指数概率密度函数,并结合核磁共振二维谱数据的先验知识,规划连续采集时域数据的位置.本文采用Tsai C M等人提出的变密度方法来获得伪随机采样模式[35]:利用笛卡尔坐标系采样方案,Monte Carlo方法产生对t1维行数抽样的随机数.概率密度函数描述采集时域数据几率的总体轮廓,分为两个部分:连续采样区域与衰减采样区域.所谓连续区域为,凡是在此区域内采集的随机数为必然事件;衰减区域则随着随机数远离连续区域,采集的概率呈现幂指数衰减.本文连续区域选取时域数据的前端,即包含数据的主要信息部分,保证重建信号的质量.概率密度函数可以表示为:
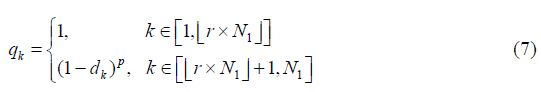
(7)式中表示随机数被采集到的概率.r为连续采集前端数据总体数据的百分比,即本文实验部分的采样半径.表示维全采的时域数据行数.,把随机数的概率分配到0~1之间.p描述衰减速率,本文p值选为3.关于采样矩阵讨论详见“不同采样模式的固体DQ-SQ实验的压缩感知重建比较”[36].
1.4 迭代软阈值算法实现流程压缩感知技术的重建过程要求信号具有稀疏性,即信号本身是稀疏的或者通过特定的变换(称为稀疏变换)能够将信号变换到稀疏域.小波变换是典型的稀疏变换,尤其是对磁共振成像领域的重建应用较为广泛[1].但对于核磁共振波谱方面,时域数据变换到频域后,谱峰的数量有限,所以谱图信号本身就具有一定的稀疏性.正因为谱图的自稀疏性,所以迭代软阈值重建算法流程的阈值处理可以选在谱图域.算法见表 1.
| 谱图域迭代软阈值重建算法流程 | ||
| 初始化 | 输入: | y:欠采时域数据 |
| $\lambda $:谱图域阈值 | ||
| 输出: | $\hat x$:重建谱图 | |
| 算法 | 初始化: | ${x^{[0]}} = {\Psi ^{ - 1}}{\rm{ + }}(y)$ |
| 迭代: | $\eqalign{ & dx = {\Psi ^{ - 1}} + [b - ({\Psi _u}{x^{[n]}})] \cr & {x^{[n + 1]}} = {x^{[n]}} + {S_\lambda }dx \cr} $ | |
| 终止 | 超出设定条件 | |
| 输出 | $\hat x$ | |
实验数据为1H DQ-SQ的时域全采样复数数据.1H DQ-SQ实验在Bruker AVANCEⅢ 600 MHz型NMR谱仪上进行,使用BABA1[2]脉冲序列,1H 90°脉宽为3.5 ms,转速为23.6 kHz,并且是转子同步采样;采样次数为80,循环等待时间为2 s,采样点阵为(其中t1维数据包括实部和虚部).本实验在Matlab2013a软件平台对数据进行处理,利用matNMR软件数据进行显示.为方便比较,图 1和图 2的x轴和y轴皆为点数(points).其中图 1的y轴用FT处理为64个点,以增加平滑度.
|
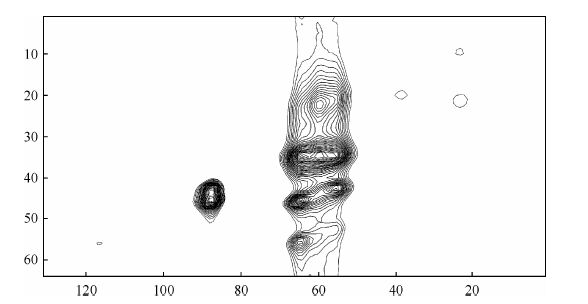
| 图 1 1H DQ-SQ二维NMR谱 Fig. 1 1HDQ-SQ NMR spectrum |
图 1显示的是全采时域数据的傅里叶频域谱图.
对于1H DQ-SQ谱数据,其峰较宽,因此t1维数据维只有48行,数据量较少,于是我们尝试仅采集50%的数据量(欠采率为50%),即欠采行数为24行.在以下的比较中,我们固定欠采率为50%,分别比较采样半径r为10%,20%,30%,40%和50%的时域数据采用不同处理方法获得的图谱.
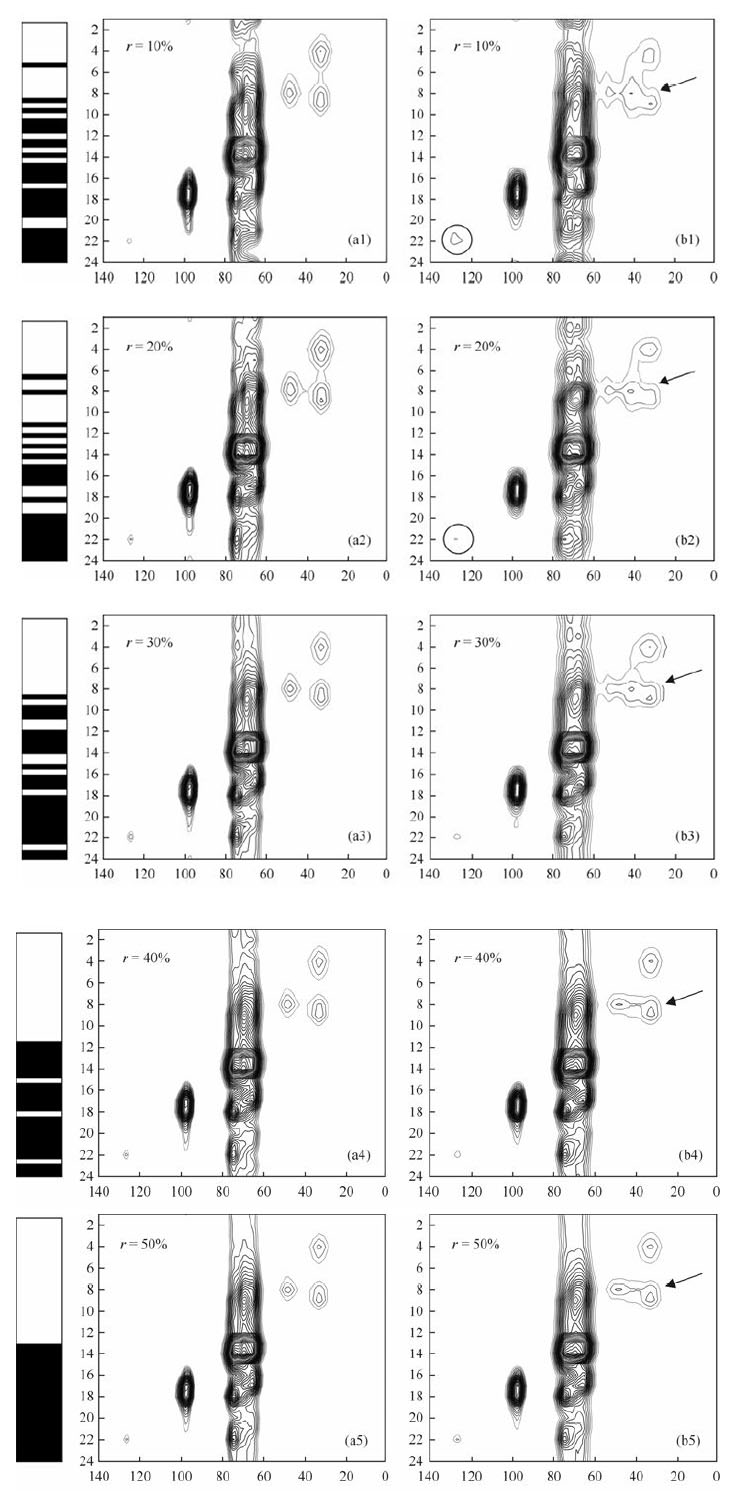
图 2第1列是采样模式矩阵(白色表示采样,黑色表示不采样,从上到下是1~48),第2列为谱图域迭代软阈值重建结果,第3列为共轭梯度方法重建结果.比较第2列和第3列可知,随着采样半径的减少共轭梯度方法重建的谱图中的弱峰逐渐消失(见r =10%,r = 20%,第3列圆圈圈出的峰),同是右上角的3个峰扩展在一起,分辨率下降,而顺序比较不同采样半径的软阈值重建结果可知,随着采样半径的增大,迭代软阈值方法的重建图保真度更高,与原图更加接近.综上所述,采用大采样半径的谱图域迭代软阈值重建方法效果最佳.
|
| 图 2 不同采样半径下的1H DQ-SQ谱在不同情况下重建.数据在欠采50%情况下,采样半径r从10%开始,每次间隔10%,直至半径达到50%为止.第1列是采样模式矩阵(白色表示采样,黑色表示不采样,从上到下是1~48),第2列为谱图域迭代软阈值重建结果.第3列为共轭梯度方法重建结果,对数据全变分后重建结果 Fig. 2 Comparison of CS reconstruction results of 1H DQ-SQ spectra with different sampling radius. The sampling rate is fixed at 50% and the sampling radius increases from 10% to 50% with a step of 10%. Left: sampling matrixes used for the reconstruction,where sampled lines are indicated by white lines; Middle: results from IST; Right: results from CG-TV |
实验数据为87Rb MQMAS的时域全采样复数数据.87Rb实验在Bruker AVANCEII 800 MHz型NMR谱仪上进行,87Rb MQMAS实验使用Split-t1和z-filter[3]脉冲序列,两个强脉冲的脉宽分别为1.8和1.2 ms,90°软脉冲的脉宽为16 ms,转速为10 kHz,并且是转子同步采样;采样次数为32,循环等待时间为1 s,采样点阵为(其中t1维数据包括实部和虚部),本实验在Matlab2013a软件平台对数据进行处理,利用matNMR软件数据进行显示.为方便比较,图 3和图 4的x轴和y轴皆为点数(points).

|
| 图 3 87Rb MQMAS二维NMR谱 Fig. 3 87Rb MQMAS NMR spectrum |

|
| 图 4 不同采样半径下的87Rb MQMAS在不同情况下重建.数据在欠采50%情况下,采样半径r从10%开始,每次间隔10%, 至半径达到50%为止.第1列是采样模式矩阵,第2列为谱图域迭代软阈值重建结果.第3列为共轭梯度方法重建结果.对数据全变分后重建结果 Fig. 4 Comparison of CS reconstruction results of 87Rb MQMAS spectra with different sampling radius. The sampling rate is fixed at 50% and the sampling radius increases from 10% to 50% with a step of 10%. Left: sampling matrixes used,where lines sampled lines are indicated by white lines while lines not sampled lines are indicated by black lines; Middle: results from IST (iterative soft thresholding); Right: results from conjugate gradient method with the total variation (CG-TV) |
图 3显示的是全采时域数据的傅里叶频域谱图.
图 4第1列是采样模式矩阵(白色表示采样,黑色表示不采样),第2列为谱图域迭代软阈值重建结果,第3列为共轭梯度方法重建结果.比较第2列和第3列箭头所指的峰可知,随着采样半径的减少共轭梯度方法重建的谱图中两个峰的分辨度在下降;而顺序比较不同采样半径的软阈值重建结果可知,随着采样半径的增大,迭代软阈值方法的重建图保真度更高,与原图更加接近.因此,87Rb MQMAS与1H DQ-SQ谱图的重建结果都说明了,采用大采样半径的谱图域迭代软阈值重建方法效果更佳.
3 结论压缩感知非线性重建算法既能大大减少采集时域数据的时间,又能恢复出真实的信号,因而在信号重建领域有着无可比拟的作用,引起了广泛的关注.本文利用压缩感知算法来重建固体1H DQ-SQ二维NMR谱和87Rb MQMAS二维NMR谱.由于这些谱是谱峰比较宽的一系列谱图,对于很多算法来讲重建起来相当困难,本文采用软阈值方法重建,并与共轭梯度方法相比较,发现谱图域软阈值重建效果大大优于共轭梯度方法;并且随着欠采半径的增加,谱图域软阈值重建效果更加明显.
| [1] | Ernst R R, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions[M]. Oxford: Oxford University Press, 1990. |
| [2] | Massiot D, Fayon F, Capron M, et al. Modelling one and two dimensional solid-state NMR spectra[J]. Magn Reson Chem, 2002, 40(1): 70-76. |
| [3] | Kazimierczuk K, Orekhov V Y. A comparison of convex and non-convex compressed sensing applied to multidimensional NMR[J]. J Magn Reson, 2012, 223: 1-10. |
| [4] | Bruschweiler R. Theory of covariance nuclear magnetic resonance spectroscopy[J]. J Chem Phys, 2004, 121(1): 409-414. |
| [5] | Daniell G J, Hore P J. Maximum entropy and NMR—A new approach[J]. J Magn Reson, 1989, 84(3): 515–536. |
| [6] | Coggins B E, Zhou P. High resolution 4-D spectroscopy with sparse concentric shell sampling and FFT-CLEAN[J]. J Biomol NMR, 2008, 42(4): 225-239. |
| [7] | Lustig M, Donoho D, Pauly J M. Sparse MRI: The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med, 2007, 58(6): 1 182-1 195. |
| [8] | Baraniuk R G. Compressive sensing[J]. IEEE Signal Proc Mag, 2007, 24(4): 118-124. |
| [9] | Foucart S, Rauhut H. A Mathematical Introduction to Compressive Sensing[M]. Berlin: Springer, 2013. |
| [10] | Donoho D L. Compressed sensing[J]. IEEE T Inform Theory, 2006, 152(4): 1 289-1 306. |
| [11] | Xu X B, Guo D, Cao X, et al. Reconstruction of self-sparse 2D NMR spectra from undersampled data in the indirect dimension[J]. Sensors (Basel), 2011, 11(9): 8 888-8 909. |
| [12] | Holland D J, Bostock M J, Gladden L F, et al. Fast multidimensional NMR spectroscopy using compressed sensing[J].Angewandte Chemie, 2011, 50(29): 6 678-6 681. |
| [13] | Candes E J, Romberg J K, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Commun Pur Appl Math, 2006, 59(8): 1 207-1 223. |
| [14] | Candes E J, Romberg J K, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE T Inform Theory, 2006, 52(2): 489-509. |
| [15] | Candes E J, Tao T. Near-optimal signal recovery from random projections: Universal encoding strategies?[J]. IEEE T Inform Theory, 2006, 52(12): 5 406-5 425. |
| [16] | Donoho D L. De-noising by soft-thresholding[J]. IEEE T Inform Theory, 1995, 41(3): 613-627. |
| [17] | Blumensath T, Davies M E. Iterative hard thresholding for compressed sensing[J]. Appl Comput Harmon Anal, 2009, 27(3): 265-274. |
| [18] | Fornasier M, Rauhut H. Iterative thresholding algorithms[J]. Appl Comput Harmon Anal, 2008, 25(2): 187-208. |
| [19] | Donoho D L, Johnstone I M. Engineering Advances: New Opportunities for Biomedical Engineers[C]. Baltimore: Proceedings of the 16th Annual International Conference of the IEEE, 1994. |
| [20] | Stern A S, Donoho D L, Hoch J C. NMR data processing using iterative thresholding and minimum l1 norm reconstruction[J]. J Magn Reson, 2007, 188(2): 295-300. |
| [21] | Steidl G, Weickert J, Brox T, et al. On the equivalence of soft wavelet shrinkage, total variation diffusion, total variation regularization, and SIDEs[J]. SIAM J Numer Anal, 2004, 42(2): 686-713. |
| [22] | Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM J Imag Sci, 2009, 2(1): 183-202. |
| [23] | Bruck J R E. On the weak convergence of an ergodic iteration for the solution of variational inequalities for monotone operators in Hilbert space[J]. J Math Anal Appl, 1977, 61(1): 159-164. |
| [24] | Passty G B. Ergodic convergence to a zero of the sum of monotone operators in Hilbert space[J]. J Math Anal Appl, 1979, 72(2): 383-390. |
| [25] | Facchinei F, Pang J S. Finite-Dimensional Variational Inequalities and Complementarity Problems[M]. New York: Springer, 2003. |
| [26] | Candes E J. Compressive sampling[C]. Madrid: Proceedings on the International Congress of Mathematicians, 2006, 1 433 -1 452. |
| [27] | Candes E J, Romberg J K. Sparsity and incoherence in compressive sampling[J]. Inverse Probl, 2006, 23(3): 969-985. |
| [28] | Nayak K S, Nishimura D G. Randomized trajectories for reduced aliasing artifact[C]. Proceedings of the 6th Annual Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM'98), 1998, 670. |
| [29] | Tsai C M, Nishimura D G. Reduced aliasing artifacts using variable-density k-space sampling trajectories[J]. Magn Reson Med, 2000, 43(3): 452-458. |
| [30] | Zheng Hui(郑慧), Han Ming-yue(韩明月), Hu Bing-wen(胡炳文), et al. Comparison of different sampling schems in compressed sensing reconstruction for DQ-SQ experiments(不同采样模式的固体DQ-SQ 实验的压缩感知重建比较)[J]. Chinese J Magn Reson(波谱学杂志), 2015, 31(4): 535-547. |
| [31] | Lustig M, Donoho D L, Santos J M, et al. Compressed sensing MRI[J]. IEEE Signal Proc Mag, 2008, 25(2): 72-82. |
| [32] | Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI[J]. Magn Reson Med, 2008, 59(2): 365-373. |
| [33] | Otazo R, Kim D, Axel L, et al. Combination of compressed sensing and parallel imaging for highly accelerated first‐pass cardiac perfusion MRI[J]. Magn Reson Med, 2010, 64(3): 767-776. |
| [34] | Ung H, Sung K, Nayak K S, et al. k - t FOCUSS: A general compressed sensing framework for high resolution dynamic MRI[J]. Magn Reson Med, 2009, 61(1): 103-116. |
| [35] | Sommer W, Demco D E, Hafner S, et al. Rotation-synchronized homonuclear dipolar decoupling[J]. J Magn Reson A, 1995, 116(1): 36-45. |
| [36] | Trebosc J, Amoureux J P, Gan Z H. Comparison of high-resolution solid-state NMR MQMAS and STMAS methods for half-integer quadrupolar nuclei[J]. Solid State Nucl Magn Reson, 2007, 31(1): 1-9. |
 2015, Vol. 32
2015, Vol. 32




