文章信息
- 张树林, 常严, 杨晓冬
- ZHANG Shu-lin, CHANG Yan, YANG Xiao-dong
- 方差评估在幅值限制脉冲优化中的应用
- Optimization of Limited Amplitude Radiofrequency Pulse with Variance Evaluation
- 波谱学杂志, 2015, 32(3): 462-469
- Chinese Journal of Magnetic Resonance, 2015, 32(3): 462-469
- http://dx.doi.org/10.11938/cjmr20150307
-
文章历史
- 收稿日期: 2014-08-14
- 收修改稿日期: 2015-07-23
2. 中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;
3. 中国科学院大学,北京 100049
2. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
脉冲序列在核磁共振领域中扮演核心角色[1],借助脉冲序列可实现样本自旋体系的量子操控,从而产生预期的核磁共振信号,进而实现样本的波谱分析或成像应用.矩形脉冲或SINC脉冲等传统脉冲存在着带宽激发不均匀、样本弛豫效应对信号衰减影响较大等鲁棒性较差的固有缺陷.绝热脉冲虽然具备抵抗射频场不均匀性的特点,但是为了满足相应的绝热条件,同非绝热脉冲相比,绝热脉冲通常需要非常高的脉冲强度,此外,其脉冲宽度也更大,由此将增加信号灵敏度的浮动、共振漂移及弛豫效应等不利影响[2].基于最优控制理论设计的优化脉冲相比较上述传统脉冲,能有效克服带宽激发不均匀、样本的弛豫效应对信号的衰减影响较大和信号灵敏度偏低弊端,已在液态核磁共振[3, 4, 5],固态核磁共振[6, 7],量子计算[8, 9, 10]和磁共振成像[11, 12]等领域中取得一系列研究成果.对优化脉冲的进一步应用发现,优化脉冲普遍存在幅值过大的问题,在限制幅值的条件下优化脉冲十分必要[13].一方面,核磁共振谱仪固有的脉冲强度或功率也是有限的,典型的脉冲强度可达几十千赫,而大部分小型核磁共振谱仪则无法提供幅值超过5 kHz的脉冲序列;另一方面,过强的脉冲会对样品造成破坏,特别是在磁共振成像领域,其对脉冲的幅值更为敏感.
另外,在特定带宽范围内的均匀激发是衡量脉冲优劣的指标之一.一方面,在三维磁共振成像领域,Z方向的梯度场提供选层的位置信息,Z方向上每一个层厚对应一个带宽.脉冲在一个带宽范围内激发不均匀会导致各个选层之间图像的重叠,进而产生图像伪影[14];另一方面,脉冲能在特定带宽范围内均匀激发,表明脉冲能克服磁场不均匀性,抵御一定程度的磁场偏移,说明其具有较好的鲁棒性.而目前针对限制幅值的脉冲优化,普遍采用的是文献[13]提出的方法,该方法以脉冲的平均激发效率为优化的目标函数.为了在优化的过程中限制脉冲的幅值,其采用了改进的最速下降法作为优化的数值迭代算法,即将优化过程中出现的大于限制值的脉冲片段替换为限制值,已达到限制幅值的效果.但是实验发现,仅将平均激发效率作为目标函数优化脉冲,虽然能提高脉冲的平均激发效率,但是得到的优化脉冲在特定带宽范围的激发均匀度却不理想.
针对上述方法的不足,提出了一种改进的方法:在目标函数中引入带权重系数的方差项,相应地计算了目标函数的梯度,仍使用修正的最速下降法作为数值迭代算法计算出优化脉冲.并进一步研究了不同权重系数以及脉冲幅值限制条件对于优化效果的影响,以达到最佳的优化效果.下面将详细介绍该方法的原理,并通过实验验证其可行性与有效性.
1 脉冲优化理论核磁共振脉冲优化指的是基于自旋磁矩的运动方程,运用最优控制理论构造优化策略,抵消带宽和射频场不均匀性等不利因素的影响,采用数值方法计算优化脉冲的过程,其流程如图 1所示.

|
| 图 1 脉冲优化流程图 Fig. 1 Flow chart of pulse optimization |
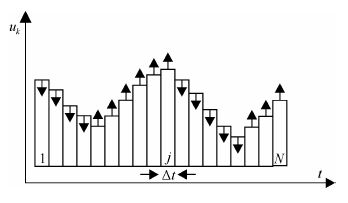
为了使研究的问题能在数值框架下求解,我们将连续的核磁共振脉冲离散化至N片段,并认为每一个离散化的脉冲片段的强度为一常数值uk(t),k值用以表征参数在x轴和y轴的分量,t标识时间[5].脉冲离散化如图 2所示.
|
| 图 2 脉冲离散化示意图 Fig. 2 Schematic representation of discretized pulse |
最优控制问题的核心是构建适当的目标函数,以离散化的脉冲片段作为优化的控制量,使目标函数值最大化.为了在优化过程能控制最终优化脉冲的激发均匀度,在使用最优控制理论构造优化模型时,在目标函数中引入带权重系数的标准方差项:


相应的标准方差可表示为:
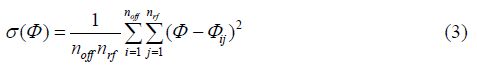
noff和nrf分别为针对带宽和射频场不均匀性选取的控制点数;其中φij为:


关于φij以及其梯度$\frac{{\partial {\Phi _{ij}}}}{{\partial {u_k}(t)}}$的计算,在文献[5]和[15]有详述,这里不再赘言;而φ的梯度值即是φij梯度的均值.
针对特定的脉冲幅值限制:$\sqrt {u_x^2(t) + u_y^2(t)} \leqslant \eta $,构造如下的数值迭代算法:
1) 选择随机的初始脉冲uk(t)以及方差权重系数.
2) 根据(1)式计算当前脉冲下的目标函数值,(5)式计算对应的梯度.
3) 按:${u_k}(t) \to {u_k}(t) + \varepsilon \frac{{\partial {\Phi ^*}}}{{\partial {u_k}(t)}}$更新脉冲uk(t).其中ε为搜索步长,如果更新的脉冲使得目标函数值变大,适当增大步长,反之减小.
4) 对于任意的uk(t),如果$\sqrt {u_x^2(t) + u_y^2(t)} > \eta $,令${u_k}(t) \to \frac{1}{{\sqrt {u_x^2(t) + u_y^2(t)} }}{u_k}(t)$.
5) 返回步骤2),迭代至收敛条件.
2 实验与讨论本文采用以上算法针对持续时间为500 μs的脉冲进行优化,考虑带宽范围-10~10 kHz,射频场不均匀性范围0.9~1.1,以单自旋1H系统磁矩实现${I_z} \to {I_x}$的最大激发为优化目标.在优化过程中,将脉冲持续时间离散化至1 μs,取81个带宽控制点,5个射频场不均匀性控制点.优化计算工作是在AMAX PSC-2N工作站上使用MATLAB 2013a软件实现的,相关实验是在一台德国PURE DEVICE 0.5 T小型研究性谱仪上完成的,实验样品是芥花籽油.
由于PURE DEVICE 0.5T小型研究性谱仪最大能提供的脉冲幅值为4 573 Hz,我们设置优化脉冲的约束条件为:$\sqrt {u_x^2(t) + u_y^2(t)} \leqslant 4{\text{ }}573\;{\text{Hz}}$.针对目标函数(1)式分别取方差权重系数λ = 0(对应传统不考虑方差项的脉冲优化方法)与λ = 50进行脉冲优化,对比引入方差项对于优化结果的影响.图 3(a)为不同权重系数下的优化脉冲波形,可以看出,引入方差项后,优化的脉冲波形有了比较大的变化,这表明了方差项的引入对优化结果的有着较大的影响.为验证引入方差项后造成的影响是否能提高激发效果,我们将上述两个优化脉冲分别施加至芥花籽油样品进行激发实验.为模拟激发需要的带宽环境,根据拉莫方程,可通过改变射频脉冲的频率以等效磁场的偏移.为此选取不同的共振偏移量依次激发获取FID信号,通过傅里叶变换获得相应共振偏移位置的波谱,进而将所有信号的峰值轮廓线作为等效的带宽激发轮廓.实验中,在带宽-10~10 kHz范围沿正负偏移方向各均匀选取20个激发测试点,依次激发描绘出脉冲的带宽激发轮廓,实验结果见图 3(b).由于图中纵坐标的数值是通过对FID信号进行傅里叶变化获得的,故可通过谱图中峰值的轮廓对比反映相应脉冲激发信号强度的差异.从实验结果可以看出,引入方差项后优化得到的脉冲虽然相对降低了带宽中心区域的激发效率,但是其通过提高脉冲在带宽边缘的激发效率,从而保证了在整个带宽范围内平均激发效率下降很小的前提下,提高了激发的均匀度.

|
| 图 3 引入方差项对优化结果的影响. (a) 权重因子分别为50和0对应的优化脉冲;(b) 权重因子分别为50和0对应优化脉冲带宽激发实验结果对比 Fig. 3 Impact of introducing the variance term to the optimization results. (a) Optimal pulses corresponding to weighting factors of 50 and 0 respectively; (b) The broadband excitation contrast between the two optimal pulse corresponding to weighting factors of 50 and 0 respectively |
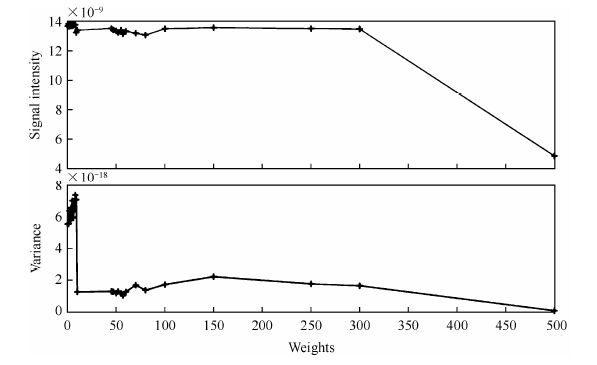
由此可见,在脉冲优化的目标函数中引入方差项能有效控制优化脉冲的激发表现.而寻找合适的方差权重系数显然是使用该方法获取理想的优化脉冲的关键.在不改变其它优化参数的前提下,图 4给出了优化脉冲带宽实验激发的平均信号强度以及对应的均匀度(即标准方差值)随着权重系数的改变的变化规律.可以看出,当方差权重系数较小(λ < 10)时,方差项对于目标函数的影响较小,优化脉冲虽然激发信号的强度较大,但是此时脉冲带宽激发的均匀度差(方差值大);随着方差权重系数的逐渐变大,方差项对于优化的影响也随之增加,当权重系数增加至10时,此时方差项对于优化结果的影响开始显著增加,在相应的脉冲激发信号强度小幅降低的同时,可显著改善了脉冲带宽激发的均匀度;而过大的权重系数优化得到的脉冲虽然有着较小的方差值(均匀度好),但是其对应的信号强度急剧降低,信噪比较差.实验发现,在权重因子为57附近,此时,脉冲带宽激发的均匀度最好,且信号强度也是处于可接受水平,是比较适宜的权重值.这表明,权重系数大小的选取对优化结果有着较大的影响,因此,需要在仪器性能(可用的最高脉冲强度)确定的情况下,依据优化参数(带宽、射频场不均匀性等)选择合适的权重系数以获得预期的激发效果.
|
| 图 4 权重系数对优化脉冲激发信号强度和均匀度的影响 Fig. 4 Impact of weights to the signal intensity and variance |
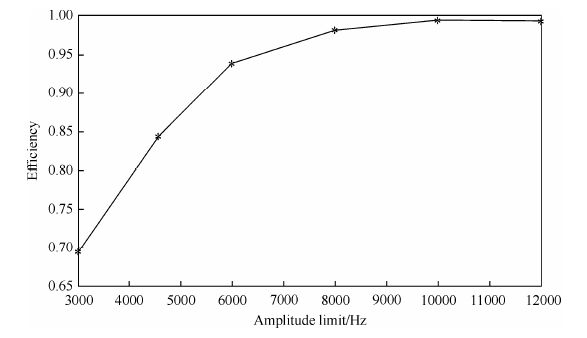
与此同时,为进一步探究限制条件对于优化脉冲的影响,同时也为了进一步验证该方法的有效性,在不改变其他优化条件参数的前提下,选取权重系数λ = 57针对不同的脉冲幅值限制条件,分别对同一初始脉冲进行优化.图 5展示了优化脉冲的带宽激发平均效率随着脉冲限制条件取3 000 Hz到12 000 Hz不同值的变化趋势.从图中可以看出,幅值限制条件是影响优化结果的一个重要条件,过于苛刻的限制条件会降低优化脉冲的激发效率,进而降低信号强度.文献[16, 17]针对有约束的脉冲优化问题进行了研究,结果表明了脉冲的持续时间越短、带宽范围和射频场不均匀性越大,优化脉冲的激发效率会越低.本文的相关结论也可作为相关研究的补充.值得注意的是,大多小型核磁共振谱仪的脉冲幅值限制条件为5 000~6 000 Hz,在该限制范围,本方法优化的到的脉冲的激发效率达0.9左右,而小型核磁共振谱仪普遍使用的传统矩形脉冲在相同的带宽范围内激发,其平均效率仅为0.4左右.通过提高带宽激发的平均效率可以获得更强的信号,提高信号的灵敏度;另一方面,提高带宽激发的均匀性可以使得谱仪能够克服主磁场不均匀性的影响,进而提高仪器的性能.
|
| 图 5 不同脉冲幅值限制值对优化结果的影响 Fig. 5 Impact of limits to the excitation efficiency |
通过上述的讨论可以看出,在目标函数中引入带权重系数的方差项这一方法可以通过调整权重系数的大小来控制脉冲的激发带宽激发轮廓,进而根据不同的激发需求选取适当的权重系数对特定的脉冲幅值限制条件的脉冲进行优化.
3 结论本文提出的在目标函数中引入带权重系数的方差项来优化脉冲的方法,可以解决过去针对有幅值限制的优化脉冲带宽激发不均匀的问题,同时也可以通过调整方差项的权重系数以获得特定的优化脉冲,以满足不同的激发需求.该方法在核磁共振相关领域,特别是在磁共振成像领域以及将优化脉冲应用到小型核磁共振设备中改善仪器的性能方面具有很好的应用前景.
| [1] | Levitt M H. Spin Dynamics: Basics of Nuclear Magnetic Resonance[M]. John Wiley & Sons, 2013. |
| [2] | Bernstein M A, King K F, Zhou X J. Handbook of MRI Pulse Sequences[M]. Elsevier, 2004. |
| [3] | Reiss T O, Khaneja N, Glaser S J. Time-optimal coherence-order-selective transfer of in-phase coherence in heteronuclear is spin systems[J]. J Magn Reson, 2002, 154(2): 192-195. |
| [4] | Khaneja N, Reiss T, Luy B, et al. Optimal control of spin dynamics in the presence of relaxation[J]. J Magn Reson, 2003, 162: 311-319. |
| [5] | Khaneja N, Reiss T, Kehlet C, et al. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms[J]. J Magn Reson, 2005, 172: 296-305 |
| [6] | Kehlet C T, Sivertsen A C, Bjerring M, et al. Improving solid-state NMR dipolar recoupling by optimal control[J]. J Am Chem Soc, 2004, 126(33): 10202-10203. |
| [7] | Tošner Z, Glaser S J, Khaneja N, et al. Effective hamiltonians by optimal control: Solid-state NMR double-quantum planar and isotropic dipolar recoupling[J]. J Chem Phys, 2006, 125(18): 184502. |
| [8] | Khaneja N, Glaser S J, Brockett R. Sub-riemannian geometry and time optimal control of three spin systems: quantum gates and coherence transfer[J]. Phys Rev A, 2002, 65(3): 032301. |
| [9] | Zhang Ya-juan(张亚娟), Xuan Ya-nan(轩亚楠), Wei Da-xiu(魏达秀). NMR experimental implementation of cluster state (Cluster态的核磁共振实验制备)[J]. Chinese J Magn Reson(波谱学杂志), 2014, 31(1): 108-115. |
| [10] | Schulte-Herbrüggen T, Spörl A K, Marx R, et al. Quantum computing implemented via optimal control: Theory and application to spin and pseudo-spin systems[J]. Lectures on Quantum Information, 2006: 481-501. |
| [11] | Xu D, King K F, Zhu Y, et al. Designing multichannel, multidimensional, arbitrary flip angle RF pulses using an optimal control approach[J]. Magnet Reson Med, 2008, 59(3): 547-560. |
| [12] | Vinding M S, Maximov I I, Tošner Z, et al. Fast numerical design of spatial-selective rf pulses in MRI using Krotov and quasi-Newton based optimal control methods[J]. J Chem Phys, 2012, 137(5): 054203. |
| [13] | Skinner T E, Reiss T O, Luy B, et al. Reducing the duration of broadband excitation pulses using optimal control with limited RF amplitude[J]. J Magn Reson, 2004, 167(1): 68-74. |
| [14] | Hashemi R H, Bradley W G, Lisanti C J. MRI: The Basics[M]. Lippincott Williams & Wilkins, 2012. |
| [15] | de Fouquieres P, Schirmer S G, Glaser S J, et al. Second order gradient ascent pulse engineering[J]. J Magn Reson, 2011, 212(2): 412-417. |
| [16] | Kobzar K, Skinner T E, Khaneja N, et al. Exploring the limits of broadband excitation and inversion pulses[J]. J Magn Reson, 2004, 170(2): 236-243. |
| [17] | Kobzar K, Skinner T E, Khaneja N, et al. Exploring the limits of broadband excitation and inversion: II. Rf-power optimized pulses[J]. J Magn Reson, 2008, 194(1): 58-66. |
 2015, Vol. 32
2015, Vol. 32




