文章信息
- 翁鹏飞,董 芳,王前锋,裴孟超,刘 田,王乙,李建奇
- WENG Peng-fei, DONG Fang, WANG Qian-feng, PEI Meng-chao, Wang Yi, Li Jian-qi
- 三维多回波流动补偿定量磁化率成像(QSM)方法研究
- Three-Dimensional Multi-Echo Quantitative Susceptibility Mapping with Flow Compensation
- 波谱学杂志, 2015, 32(3): 450-461
- Chinese Journal of Magnetic Resonance, 2015, 32(3): 450-461
- http://dx.doi.org/10.11938/cjmr20150306
-
文章历史
- 收稿日期:2014-08-26
- 收修改稿日期:2015-07-23
2. MedImageMetric, LLC, New York, USA;
3. Radiology, Weill Medical College of Cornell University, New York, USA;
4. Biomedical Engineering, Cornell University, New York, USA
2. MedImageMetric, LLC, New York, USA;
3. Radiology, Weill Medical College of Cornell University, New York, USA;
4. Biomedical Engineering, Cornell University, New York, USA
磁化率是描述磁介质性质的宏观标量,其数值大小不仅能反映生物组织的物理特性,还可以提供丰富的病理信息,因此磁化率对临床诊断有重要的意义[1].定量磁化率成像(Quantitative Susceptibility Mapping,QSM)利用一般成像技术舍弃的相位信息得到局部磁场变化特性,通过复杂的场到源反演计算,可直接得到定量的磁化率图[2, 3, 4, 5, 6, 7].在临床和科研领域,QSM能够提供丰富的解剖和病理信息,因此被广泛应用于诊断脑铁沉积[8, 9, 10]、组织钙化[11, 12]、脑部微出血[13]等方面.
血氧含量能够反映出呼吸系统和循环系统是否正常.对于大脑而言,持续的氧输送能够维持脑组织正常的功能与活力,因此血氧饱和度作为一种生物学标记可以反映出大脑是否发生病变,如多发性硬化症[14]、脑肿瘤[15, 16]、脑中风[17, 18, 19]等.由于脱氧血红蛋白的浓度与磁化率之间呈线性相关,因此QSM技术作为一种无创准确的定量方法可应用于定量测量血氧饱和度[20, 21, 22].
然而对于血流成像,血管内血液流动会引起相位错误,产生显著的流动伪影,最终导致定量磁化率错误.具体而言,QSM基于多回波梯度回波(GRE)序列采集的相位图,静止组织的相位值与回波时间(TE)呈线性相关.但是流动效应会破坏这种线性相关性,导致相位错误.
本文报道了在3 T磁共振系统上实现三维多回波流动补偿梯度回波序列,并用该序列采集流动水模和志愿者颅脑数据进行研究分析.实验结果表明,该方法在流动伪影矫正、相位矫正、准确测量血管内磁化率值等方面有明显的效果.
1 理论 1.1信号模型[22]未施加流动补偿的情况下,磁共振成像采集到流动质子的信号S(t)可以表示成:



从(2)式可以看出,φ1是一个关于TE的二次方程,当流速较小时,二次项$\frac{1}{2}\gamma v({r_0})\nabla \delta B({r_{TE}})T{E^2}$与一次项$\gamma \delta B({r_{TE}})TE$相比小得多,可以忽略掉,则φ1与TE呈线性相关;(3)式中k(TE)表示K空间的位置,M(TE)表示G(τ)在TE时刻的一阶磁矩,如果施加流动补偿梯度能够消除一阶磁矩,即M(TE) = 0,则φ2就不会受到流动的影响.
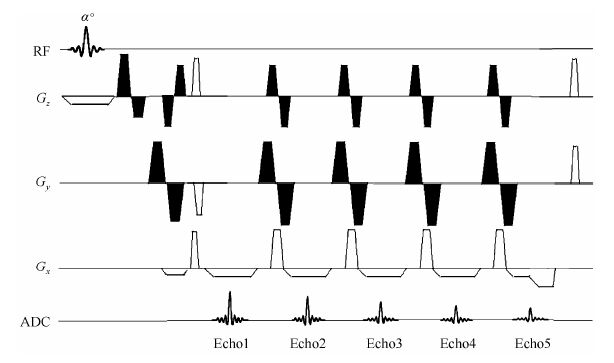
1.2 流动补偿模型[22, 23]为了补偿流动导致的相位误差,可采用如图 1所示的梯度设计.在相位编码(Gy)方向和选层(Gz)方向施加正负梯度极性对作为流动补偿梯度;读梯度(Gx)方向,采用偶回波回聚原理在第一个回波之前施加了一个流动补偿梯度.这样,对3个方向都可完成了零阶和一阶补偿.
|
| 图 1 三维多回波流动补偿梯度回波序列时序图(黑色表示补偿梯度正负极性对) Fig. 1 Schematic of 3D multi-echo flow compensated GRE sequence (compensation gradients shaded in dark) |
流动补偿对3个方向的梯度施加有如下要求(0时刻表示施加射频脉冲的峰值时刻,nTE表示第n个回波中心时刻):
读梯度方向:
$\int_0^{TE} {{G_x}(t){\text{d}}t = 0} ,{\text{ }}\int_n^{(n + 1)TE} {{G_x}(t){\text{d}}t = 0{\text{ }}(n > 0)} ,{\text{ }}\int_n^{(n + 1)TE} {{G_x}(t)t{\text{d}}t = 0} ,$
相位编码方向:
$\int_0^{TE} {{G_y}(t){\text{d}}t = \frac{{{K_y}}}{\gamma }} ,{\text{ }}\int_{(n - 1)TE}^{nTE} {{G_y}(t){\text{d}}t = 0{\text{ }}(n > 1)} ,{\text{ }}\int_0^{nTE} {{G_y}(t)t{\text{d}}t = 0} ,$
选层方向:
$\int_0^{TE} {{G_z}(t){\text{d}}t = \frac{{{K_z}}}{\gamma }} ,{\text{ }}\int_{(n - 1)TE}^{nTE} {{G_z}(t){\text{d}}t = 0{\text{ }}(n > 1)} ,{\text{ }}\int_0^{nTE} {{G_z}(t)t{\text{d}}t = 0} ,$
由流动补偿公式[23]可知,零阶补偿和一阶补偿可表示为:


对于读梯度方向,利用读梯度的偶回波回聚原理[23]进行补偿,使磁矩${m_{x0}}(t) = 0$并且${m_{x1}}(t) = 0$.相位编码方向和选层方向流动补偿方式相似,以相位编码方向为例进行演算,如图 2所示.为了计算流动补偿梯度的幅度,对参数作如下定义:假设梯度上升沿均为t¢;相位编码梯度平台期为ty,幅度为Gy,相位编码梯度结束到第一个回波中心的时间为t1;流动补偿梯度幅度为Gnfc,表示第n个回波,平台期为t2,正负梯度对分别用Gnfc+和Gnfc-表示.

|
| 图 2 相位编码方向流动补偿示意图(黑色表示补偿梯度正负极性对) Fig. 2 Schematic of phase encoding direction with flow compensation (compensation gradients shaded in dark) |
对第一个回波(回波中心时刻为时间零点),推算过程如下:
由于G1fc+和G1fc-大小相等方向相反,在相同的时间内对时间积分之和为0,即$\int_0^{TE} {{G_{1fc + }}{\text{d}}\tau + } {G_{1fc - }}{\text{d}}\tau = 0$.因此(4)式可简化为

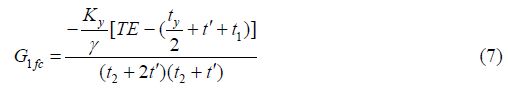
对其后第n个回波(n > 2,回波中心时刻为时间零点),演算过程同第一个回波,零阶补偿简化后可表示为:

将一阶补偿置0后,得到流动补偿梯度为:

根据以上计算结果,分别在扫描的3个方向施加流动补偿梯度,实现零阶和一阶补偿,可消除(3)式中$\gamma v({r_0})M(TE)$项.在流速较小的情况下,经过补偿后的相位与TE呈线性相关.
2 材料与方法所有实验均采用3 T磁共振成像设备系统(西门子MAGNETOM Trio a Tim 3 T),其软件版本为syngo MR B17,采用12通道头线圈作为信号接受线圈.
实验采用填满琼脂粉的立方体有机玻璃作为流动水模(长×宽×高 = 15 cm × 15 cm × 15 cm).一根内外径为4 mm/6 mm的U型橡胶导管置于水模内,导管与可调流速的蠕动泵相连.蠕动泵产生一个15 cm/s(人体静脉流速大约为10 cm/s~20 cm/s)[24]的流速后,将整个水模装置置于3 T磁共振设备系统中进行实验.
人体扫描招募健康志愿者4名(3名男性,1名女性),年龄为21~26岁.
2.1 脉冲序列的实现在西门子脉冲序列开发平台(Integrated Development Environment for Applications,IDEA)上开发三维多回波流动补偿序列[25],如图 1所示.分别在相位编码(Gy)方向、选层(Gz)方向和读梯度(Gx)方向施加了流动补偿梯度,实现三维流动补偿.
2.2 MRI扫描参数设置分别采用施加与未施加流动补偿序列采集志愿者颅脑矢状位和横断位数据,扫描参数均为:重复时间(TR) = 52 ms,回波时间(TE) = 9 ms / 18 ms / 27 ms / 36 ms / 45 ms,翻转角(FA) = 15°,观察野(FOV) = 240 mm,层厚(slice thickness) = 2 mm,层数(slice per slab) = 64层,扫描矩阵(matrix) = 256 × 256(相位编码×频率编码),分辨率(resolution) = 0.9 mm × 0.9 mm × 2 mm,每个序列扫描时间为14 min 6 s.
采用施加与未施加流动补偿序列采集流动水模冠状位数据时,扫描参数为:层数 = 32层,其他扫描参数与上述三维多回波流动补偿序列一致,每个序列扫描时间为7 min 3 s.
2.3 数据处理与分析 2.3.1 流动水模数据处理与分析分别对施加与未施加流动补偿梯度序列采集的流动水模冠状位图像进行分析.对于模图,分析比较流动伪影对图像的影响.对于相位图,首先对相位图实现时间解缠绕,选择存在流动伪影的区域作为感兴趣区域(Region of Interest,ROI),对ROI内体素的相位值进行多回波线性拟合,对比分析流动对相位的影响以及流动补偿对相位的矫正.
2.3.2 志愿者颅脑数据处理与分析对于志愿者颅脑矢状位扫描图像,分析流动伪影对模图图像质量的影响.
对于志愿者颅脑横断位扫描图像,选取最理想的一层,在上矢状窦静脉区域取10个体素作为统一的ROI进行具体分析,ROI面积为(4.5 mm × 1.8 mm = 8.1 mm2),基本覆盖横断位上所能看见的上矢状窦静脉.模图上,对ROI区域内信号强度进行测量,得到信号随回波时间衰减曲线,并按下列公式拟合得到T2和e指数衰减曲线[26, 27].

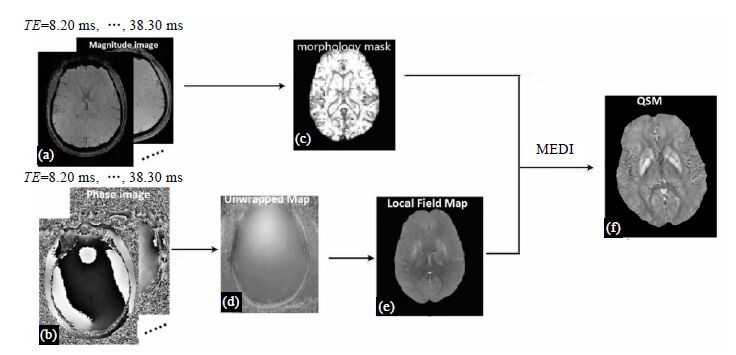
采用MEDI (Morphology Enabled Dipole Inversion)方法重建颅脑横断位QSM图像[28, 29, 30],其流程示意图如图 3所示.通过多回波模图[图 3(a)]计算得到形态学掩模[图 3(c)];利用多回波相位图[图 3(b)]线性拟合并在空间上进行相位解缠绕获得磁场分布图[图 3(d)],然后去除背景场得到局部磁场分布图[图 3(e)].局部磁场分布图[图 3(e)]和形态学掩模[图 3(c)]经过MEDI算法处理后得到QSM图像[图 3(f)].在QSM图像上分析图像信号均匀性以及流动产生的相位错误对QSM的影响.
|
| 图 3 MEDI方法重建QSM流程图 Fig. 3 Flow chart of the QSM reconstruction with MEDI methods |
图 4为水模在流速为15 cm/s的情况下采用未施加与施加流动补偿序列采集的冠状位图像.图像中箭头所示区域清楚显示;未施加流动补偿,图像上有明显的伪影,随着回波时间的增加,伪影更加显著,最后两个回波图像已经发生畸变[图 4(a)];施加流动补偿后,流动伪影明显消除,并且随着回波时间的增加,改善效果更加明显,最后的两个回波图像与第一个回波图像基本一致,图像畸变消除[图 4(b)].流动水模实验表明,流动补偿能够很好的消除由于流动产生的图像伪影和畸变.

|
| 图 4 同一层面不同回波时间流动水模冠状位图像. (a) 不加流动补偿;(b) 加流动补偿 Fig. 4 Coronal images of flow phantom in different echo time. (a) without flow compensation; (b) with flow compensation (a) Without flow compensation (b) With flow compensation |
图 5表示流动水模相位图实现时间解缠绕后,在伪影区域取ROI(图 4中箭头所示),对ROI内的相位值进行多回波线性拟合的曲线图.由于模图上有明显的流动伪影,因此相位值也一定受到影响.从未施加流动补偿相位拟合直线可以看出,相位值在第三个回波处发生跳跃,导致相位错误,数据点与拟合直线的吻合度差[图 5(a)];施加流动补偿以后,相位值基本上呈线性相关[图 5(b)],相位错误得到明显的纠正.

|
| 图 5 流动水模同一位置像素点(图 4箭头所示区域)多回波相位线性拟合曲线图. (a) 不加流动补偿; (b) 加流动补偿 Fig. 5 Comparison of multi-echo phase data from flow phantom without (a) and with (b) flow compensation |
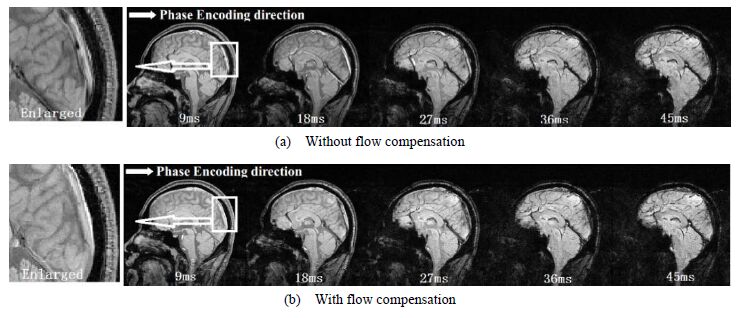
图 6是一例健康志愿者在施加流动补偿前后采集的颅脑矢状位图像.对第一个回波(TE = 9 ms),上矢状窦静脉区域进行局部放大.未施加流动补偿时,上矢状窦静脉在相位编码方向有明显的流动伪影,静脉内的信号强度分布杂乱,静脉周围脑实质模糊不清[图 6(a)];施加流动补偿后,上矢状窦静脉区域伪影明显消除,信号空间分布更加均匀[图 6(b)].
|
| 图 6 同一层面不同回波颅脑矢状位图像. (a) 不加流动补偿;(b) 加流动补偿 Fig. 6 Brain sagittal images of the same slice without (a) and with (b) flow compensation in different echo time |
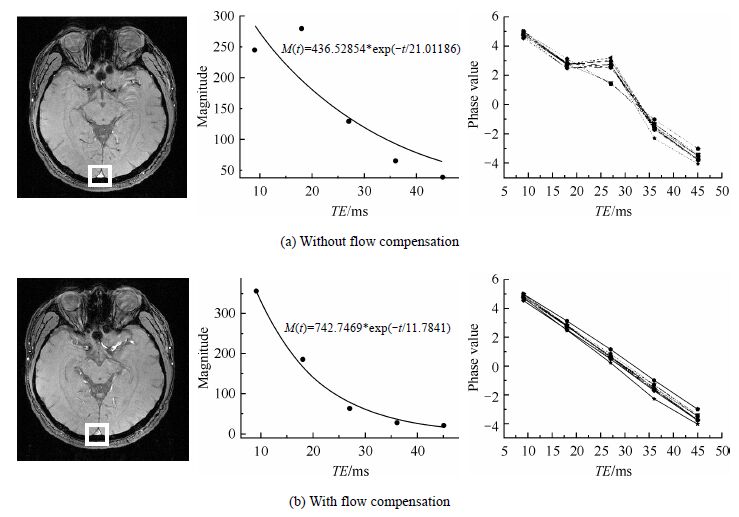
图 7是未施加与施加流动补偿采集的颅脑横断位同一层面图像以及上矢状窦静脉(图中白色矩形线框所示)部位像素幅度和相位随回波变化曲线.从幅度衰减曲线上可以看出,未施加流动补偿,第二个回波信号强度大于第一个回波,与信号强度随回波时间按e指数衰减不符[图 7(a)];施加流动补偿后,这种错误得到明显的纠正,拟合的曲线更加符合e指数衰减[图 7(b)].相位值在第三个回波时发生跳跃,导致相位值错误[图 7(a)];施加流动补偿后,相位值的错误得到明显纠正,相位随回波时间变化的线性度更好[图 7(b)].
|
| 图 7 同一层面未施加(a)与施加(b)流动补偿采集的颅脑横断位图像以及上矢状窦静脉(图中白色矩形线框所示)部位像素幅度和相位随回波变化曲线 Fig. 7 Comparison of multi-echo magnitude and phase data from the superior sagittal sinus vein without (a) and with (b) flow compensation |
图 8是一例健康志愿者的颅脑横断位通过MEDI方法重建的QSM图像.实验结果显示:QSM图像在未施加流动补偿时,上矢状窦静脉区域信号模糊不清[图 8(a)];而施加流动补偿后,上矢状窦静脉区域信号空间分布更加均匀[图 8(b)].因此,流动补偿可以矫正流动引起的相位错误,最终提高QSM的质量和准确性.

|
| 图 8 同一层面颅脑横断位QSM图像. (a) 未施加流动补偿;(b) 施加流动补偿 Fig. 8 Brain axial QSM image of the same slice without (a) and with (b) flow compensation |
流动会引起的显著的相位错误和图像伪影,最终导致QSM的错误.针对这一问题,本文在3T MRI系统中实现了三维多回波流动补偿梯度回波序列,并用该序列采集流动水模和志愿者颅脑数据.实验结果证明,流动补偿可以明显的矫正相位错误,消除流动伪影,提高QSM的准确性和可靠性.
血氧饱和度作为一种生物学标记不仅可以反映大脑是否发生病变,还可以检查呼吸系统、循环系统是否正常以及周围环境是否缺氧.在医学上测量血氧饱和度的方法大致可分为:有创检测和无创检测.有创检测又可以分为血气分析法和分光光度计法[31],均需直接抽取病人的血液,给病人带来极大的痛苦.无创检测是利用脱氧血红蛋白和氧和血红蛋白对红光和红外光区有独特的吸收光谱特性来进行检测,常规的检测技术为脉搏式血氧饱和度测量技术[32].然而无论哪种技术对光的波长等条件要求苛刻、准确性不高,更不可能很好地检测颅脑内血管的血氧饱和度.因此,传统的医学方法对于测量颅脑内血管的血氧饱和度有一定的局限性.磁共振成像技术可以准确无创采集活体信息,为临床和科研提供了一种很好的方法.近年来,QSM技术利用脱氧血红蛋白的浓度与磁化率呈线性相关的特性,作为一种准确无创的技术手段越来越多的应用于测量定量血氧饱和度[20, 21, 22].通过三维流动补偿技术消除流动引起的相位错误,使QSM的测量结果更加准确可靠,为临床应用提供更加丰富、及时的病理信息.
从信号模型中可以看出,由于空间磁场不均匀,流动组织的相位是关于回波时间的二次方程[22].本文考虑到水模和所测静脉流速较慢,二次项系数$\frac{1}{2}\gamma v({r_0})\nabla \delta B({r_{TE}})$表现不明显,因此相位呈现较好的线性相关,更精确地计算最好同时考虑二次项.线性相关的拟合结果足以证明流动补偿可以纠正流动导致的相位错误,这一点在QSM图中得到了很好的证实.本文的方法和结论仅仅是我们第一阶段的工作,因此还未涉及定量测量血管内的磁化率值和血氧饱和度,我们将在下一阶段完成这一系列的工作.最后,本文的三维流动补偿序列也存在一定缺陷,比如回波时间较长导致后面回波采集到的信号强度较弱,今后的工作将在各方面进一步完善.
综上所述,采用三维多回波流动补偿技术可以有效纠正相位错误,消除流动伪影,提高QSM的准确性和可靠性.该技术可以应用于测量颅脑静脉血氧饱和度.
| [1] | Haacke E M, Xu Y, Cheng Y C, et al. Susceptibility weighted imaging (SWI)[J]. Magn Reson Med, 2004, 52(1): 612-618. |
| [2] | Liu T. Spincemaille P, de Rochefort L, et al. Calculation of susceptibility through multiple orientation sampling (COS-MOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI[J]. Magn Reson Med, 2009, 61(1): 196-204. |
| [3] | Liu T, Wisnieff C, Lou M, et al. Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping[J]. Magn Reson Med, 2013, 69(2): 467-476. |
| [4] | Ferdinand S, Andreas D, Berengar W L, et al. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism?[J]. Neuroimage, 2011, 54(4): 2 789-2 807. |
| [5] | de Rochefort L, Liu T, Kressler B, et al. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging[J]. Magn Reson Med, 2010, 63(1): 194-206. |
| [6] | Li J Q, Chang S X, Liu T, et al. Reducing the object orientation dependence of susceptibility effects in gradient echo MRI through quantitative susceptibility mapping[J]. Magn Reson Med, 2012, 68(5): 1 563-1 569. |
| [7] | Wang A-li(王阿莉), Lin Jian-zhong(林建忠), Liu Wei-jun(刘伟俊), et al. Quantitative susceptibility mapping(定量磁化率成重建方法及其应用)[J]. Chinese J Magn Reson(波谱学杂志), 2014, 31(1): 133-154. |
| [8] | Bilgic B, Pfefferbaum A, Rohlfing T W, et al. MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping[J]. Neuroimage, 2012, 59(3): 2 625-2 635. |
| [9] | Tan H, Liu T, Wu Y, et al. Evaluation of iron content in human cerebral cavernous malformation using quantitative susceptibility mapping[J]. Invest Radiol, 2014, 49(7): 498-504. |
| [10] | Lim I A, Faria A V, Li X, et al. Human brain atlas for automated region of interest selection in quantitative susceptibility mapping: application to determine iron content in deep gray matter structures[J]. Neuroimage, 2013, 82: 449-469. |
| [11] | Deistung A, Schweser F, Wiestler B, et al. Quantitative susceptibility mapping differentiates between blood depositions and calcifications in patients with glioblastoma[J]. PLoS One, 2013, 8(3): e57924. |
| [12] | Chen W, Zhu W, Kovanlikaya I, et al. Intracranial calcifications and hemorrhages: Characterization with quantitative susceptibility mapping[J]. Radiology, 2014, 270(2): 496-505. |
| [13] | Liu T, Surapaneni K, Lou M, et al. Cerebral microbleeds: burden assessment by using quantitative susceptibility mapping[J]. Radiology, 2012, 262(1): 269-278. |
| [14] | Ge Y, Zhang Z, Lu H, et al. Characterizing brain oxygen metabolism in patients with multiple sclerosis with T2-relaxation-under-spin-tagging MRI[J]. J Cereb Blood Flow Metab, 2012, 32(3): 403-412. |
| [15] | Nordsmark M, Bentzen S M, Rudat V, et al. Prognostic value of tumor oxygenation in 397 head and neck tumors after primary radiation therapy. An international multi-center study[J]. Radiother Oncol, 2005, 77(1): 18-24. |
| [16] | Leenders K L, Beaney R P, Brooks D J, et al. Dexamethasone treatment of brain tumor patients: effects on regional cerebral blood flow, blood volume, and oxygen utilization[J]. Neurology, 1985, 35(11): 1 610-1 616. |
| [17] | Baron J C, Bousser M G, Rey A, et al. Reversal of focal “misery-perfusion syndrome” by extra-intracranial arterial bypass in hemodynamic cerebral ischemia. A case study with 15O positron emission tomography[J]. Stroke, 1981, 12(4): 454-459. |
| [18] | Sobesky J, Zaro W O, Lehnhardt F G, et al. Does the mismatch match the penumbra? Magnetic resonance imaging and positron emission tomography in early ischemic stroke[J]. Stroke, 2005, 36(5): 980-985. |
| [19] | Heiss W D, Kracht L, Grond M, et al. Early [(11)C] Flumazenil/H(2)O positron emission tomography predicts irreversible ischemic cortical damage in stroke patients receiving acute thrombolytic therapy[J]. Stroke, 2000, 31(2): 366-369. |
| [20] | Haacke E M, Tang J, Neelavalli J, et al. Susceptibility mapping as a means to visualize veins and quantify oxygen saturation[J]. J Magn Reson Imaging, 2010, 32(3): 663-676. |
| [21] | Ferdinand S,Karsten S, Andreas D, et al. Quantitative susceptibility mapping for investigating subtle susceptibility variations in the human brain[J]. Neuroimage, 2012, 62(3): 2 083-2 100. |
| [22] | Xu B, Liu T, Spincemaille P, et al. Flow compensated quantitative susceptibility mapping for venous oxygenation imaging[J]. Magn Reson Med, 2013, 72(2): 438-445. |
| [23] | Haacke E M. Magnetic Resonance Imaging: Physical Principle and Sequence Design (2nd ed.)[M]. America: John Wiley &Sons, 1999. |
| [24] | Yamada K, Naruse S, Nakajima K, et al. Flow velocity of the cortical vein and its effect on functional brain MRI at 1.5 T: preliminary results by cine-MR venography [J]. J Magn Reson Imaging, 1997, 7(2): 347-352. |
| [25] | Dong Fang(董芳), Pei Meng-chao(裴梦超), Wang Qian-feng(王前锋), et al. Gradient echo imaging of the human brain: respiratory induced artifacts and navigator echo correction(颅脑梯度回波成像: 呼吸伪影和导航回波矫正)[J]. Chinese J Magn Reson(波谱学杂志), 2014, 31(3): 321-330. |
| [26] | Chavhan G B, Babyn P S, Thomas B, et al. Principles, techniques, and applications of T2*-based MR imaging and its special applications[J]. Radiographics, 2009, 29(5): 1 433-1 449. |
| [27] | Liu Z, Liao H, Yin J, et al. Using R2* values to evaluate brain tumours on magnetic resonance imaging: preliminary results[J]. Eur Radiol, 2014, 24(3): 693-702. |
| [28] | Liu T, Xu W, Spincemaille P, et al. Accuracy of the morphology enabled dipole inversion (MEDI) algorithm for quantitative susceptibility mapping in MRI[J]. IEEE Trans Med Imaging, 2012, 31(3): 816-824. |
| [29] | Liu J, Liu T, de Rochefort L, et al. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map[J]. Neuroimage, 2012, 59(3): 2 560- 2 568. |
| [30] | Liu T, Liu J, de Rochefort L, et al. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging[J]. Magn Reson Med, 2011, 66(3): 777-783. |
| [31] | Comroe J H Jr. Textbook the Lung: Clinical Physiology and Pulmonary Function Tests (2nd ed.)[M]. Chicago: Year Book Medical Publishers, 1955. |
| [32] | Wang X F, Zhao W J. Measurement of multi-wavelength pulse oxygen saturation based on dynamic spectroscopy[J]. Spectrosc Spect Anal, 2014, 34(5): 1323-1326. |
 2015, Vol. 32
2015, Vol. 32




