文章信息
- 郝敏, 赵越超, 毛云峰, 宋永臣
- HAO Min, ZHAO Yue-chao, MAO Yun-feng, SONG Yong-chen
- 应用MRI研究CO2在癸烷中的扩散
- Diffusion of CO2 in Decane Studied by Magnetic Resonance Imaging
- 波谱学杂志, 2015, 32(3): 430-438
- Chinese Journal of Magnetic Resonance, 2015, 32(3): 430-438
- http://dx.doi.org/10.11938/cjmr20150304
-
文章历史
- 收稿日期: 2014-05-22
- 收修改稿日期: 2015-07-28
2. 大连理工大学 海洋能源利用与节能教育部重点实验室,辽宁 大连 116024;
3. 青海油田格尔木炼油厂,青海 格尔木 816000
2. Key Laboratory of Ocean Energy Utilization and Energy Conservation of Ministry of Education, Dalian University of Technology, Dalian 116024, China;
3. Qinghai Oilfield Golmud Refinery, Golmud 816000, China
近几年来,CO2强化采油(CO2-EOR)技术发展迅速,研究表明,将CO2注入油层,不仅能大幅提采收率,而且能实现CO2地质封存[1],满足环保和油藏高效开发的双重要求.CO2注入油藏时,传质是发生的第一机制,CO2在原油中的传质直接决定CO2的驱油效果,分子扩散系数是描述注入气与地层原油之间动态质量传递快慢的重要参数[2].研究气液扩散过程,合理确定分子扩散系数对CO2-EOR项目的工程设计和规划等是十分必要的.
气体在液体中的扩散系数是通过实验获得的,已提出了很多测试方法,较常用的方法是压力衰减法(又称PVT法),该方法具有所需实验装置简单,易于操作,计算求解便捷等特点,是由Riazi[3]开发的,Zhang等人[4]进行了改进,为弥补系统易于漏气的缺点,Davis等人[5]在此基础上开发了双室压力衰减法,该方法通过拟合压力衰减曲线可求得整体扩散系数.近年来X光CT技术开始应用到研究扩散问题[6, 7, 8, 9],通过CT技术,气体在液体中的扩散过程可以实现可视化,气体的扩散系数也可以通过数字技术获得.但是,CT测量面临着许多的问题,如需要造影剂、图像重影等.对于CT技术,核磁共振技术是一种实用和强大的分析工具,张宗富等人[10]应用核磁共振技术考察了水分子在单孔隙及多孔隙介质中扩散受限的程度,李新军等人[11]应用核磁共振技术提出了一种技术效率高、耗时短的扩散-横向弛豫二维反演算法,在不影响反演结果准确性的基础上极大了提高计算效率.在这篇论文中,将核磁共振技术与双室压力衰减法相结合,研究CO2在癸烷中的扩散规律.
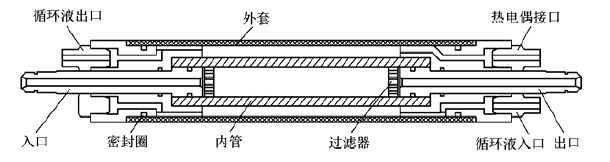
1 实验部分 1.1 实验装置图 1是实验装置的简化示意图.这项研究中所用核磁共振装置为美国Varian公司生产的9.4 T/400型超导宽腔磁体磁共振成像仪.磁体内径为89 mm,探头内径为 40 mm,可以进行1H成像研究,最高磁场梯度为0.005 T/cm.MRI样品容器是由聚酰亚胺制造,用来盛装扩散样品,最高可承受压力12 MPa,样品容器示意图如图 2所示.容器中样品的温度通过循环器向夹套中供给循环热流体实现控制,循环器是德国Julabo公司产的F-25ME型循环器,温控范围在-45~200 ℃,误差±0.5 ℃,对样品容器控温的热电偶是日本Nagano公司生产的铠装热电偶,精度为±0.1 ℃,循环液采用美国3M公司的氟化液FC-40,该液体不含氢元素因此不会干扰MRI成像[12].双室压力系统中,使用美国ISCO公司高压精密计量泵将CO2气体注入到气瓶中,气瓶外面设有配套定制的电加热保温罩.

|
| 图 1 实验装置示意图 Fig. 1 Schematic diagram of experimental apparatus |
1.2 实验材料
实验中使用的CO2由大连大特燃气有限公司提供,纯度为99.999%.实验中使用的癸烷是为阿拉丁牌正癸烷,浓度为99%.
1.3 实验测量方法本实验测定的是27 ℃下,中间容器压力设置为2 500 kPa时,CO2在大体积癸烷中的扩散.
实验开始前在8 MPa下进行气密性检测5 h,确定不漏气后方可开始实验.
(1) 扩散实验开始前,在内径为10 mm的平底玻璃试管中注入20 mm高的癸烷,然后将试管放入样品容器中,连接好装置,之后利用温控系统分别开始对样品容器和气瓶控温在25 ℃;
(2) 确定温度恒定并关闭气瓶通向样品容器的阀门后,用ISCO泵向气瓶注入CO2气体使其达到2 500 kPa,然后切断气瓶与ISCO泵的连接;
(3) 设定MRI参数,先采集一张纯液体的图像,然后打开气瓶和样品容器之间的阀门,向样品容器中注入CO2,开始采集扩散过程的MRI图像;
(4) 扩散过程达到平衡后,将压力数据和MRI数据拷贝并保存好,关闭连接气瓶和样品容器的阀门,缓慢打开排空阀泄压到常压;
扩散过程中,分别采集二维图像和一维图像.二维图像用于实验现象分析,一维图像用于计算分析.二维成像实验采用标准多层面自旋回波脉冲序列(SEMS),具体二维成像参数为:恢复时间为5 s,回波时间为4.9 ms,成像视野为40×40 mm2,像素矩阵为96×96,片选厚度为2 mm,片选为1,空间分辨率为0.41×0.41×2 mm3,累加次数为1,成像时间为8 min.一维图像成像时间为5 s,成像间隔时间为24 min.
2 实验结果分析与讨论 2.1 扩散过程实验现象分析图 3为初始压力2 282 kPa,温度为27 ℃时,CO2在正癸烷中扩散过程的部分MR二维图像.应用Imagej软件对MR图像叠加后裁剪成宽为10.94 mm,高为27.19 mm的图像,以减少多余的黑色背景.从图中可以发现,随着扩散的进行MR图像变暗,这是因为CO2不能成像[14],图中比较亮的区域表明癸烷含量较高,对应的MRI信号强度较高,同时,比较暗的区域表明癸烷含量较低,图中表明,后续时间的癸烷含量低于早些时间的癸烷含量.另外,从图中还可以发现,后续时间的液面高度高于早些时间的液面高度,这是因为CO2的扩散引起了癸烷体积的膨胀.

|
| 图 3 扩散过程的部分MR二维图像 Fig. 3 2D MR images of the part of the diffusion process |
在扩散过程中,由于CO2的扩散,信号强度下降,根据MRI信号,在位置z和时间t的CO2浓度,${C_{z,t}}$可以表达为以下形式:


在位置z和时间t,CO2在油品中的浓度分布可以写成以下形式:

MRI可实现扩散过程的可视化,由MRI获得的信号强度分布反映了流体内部的真实信息,因此由信号强度分布间接获得的CO2的浓度分布,代表了流体内部CO2浓度分布的真实情况,这个真实情况已包含溶液体积变化带来的影响.
图 4显示的是使用(4)式根据MR一维图像计算得出的不同时间下CO2在癸烷中扩散的规范化浓度分布.从图中可以发现CO2浓度沿扩散方向降低,且扩散后期的CO2浓度大于扩散前期的CO2浓度.

|
| 图 4 扩散过程的无量纲浓度分布 Fig. 4 Distribution of dimensionless content during the diffusion process |
扩散系数由菲克定律计算求得,与浓度有关的扩散方程可表示为:

(5)式中必须包括扩散系数和浓度之间的关系,否则求解是不可能的,本研究利用扩散过程中浓度变化的实验结果,采用有限体积法进行求解.
如图 5所示[15],将中间定义域离散化为尺寸为Δx及时间步长为Δt的网格,其中每个网格点$xi = i \times \Delta x(i = 0,1, \cdots ,N,N \times \Delta x = 1)$,$tn = n \times \Delta t(n = 0,1,2, \cdots )$.

|
| 图 5 有限体积模型分析方法 Fig. 5 Model of finite volume analytical method |
离散方程如下:
内点
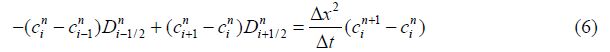
边界A

边界B
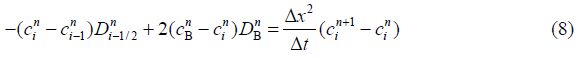
图 6显示的是由(6)~(8)式计算得出的不同时间下扩散系数与扩散距离的关系,为更清晰的显示数据变化趋势,将图 6(a)中部分数据再次显示在图 6(b)中,从图中可以发现,靠近扩散边界处,扩散系数具有较大的值,这是由界面的高传质率引起的.另外,从图中还可发现,扩散系数随扩散时间的增加而减小.

|
| 图 6 不同时间下扩散系数与扩散距离的关系 Fig. 6 Relationship between diffusion coefficient and diffusion distance at different time |
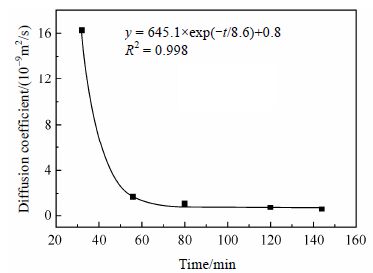
图 7显示的是根据图 6得出的扩散系数与扩散时间的关系曲线,从图中可观察到扩散系数随扩散时间呈指数趋势下降,相关系数为0.998,初始时刻扩散系数下降较快,这是因为受“潜伏期”影响[16],初始时刻溶液内部具有较大的密度梯度和浓度梯度,所以具有较大的扩散系数,随着扩散时间的增加,密度梯度和浓度梯度减小,扩散系数减小,扩散趋于平衡.
|
| 图 7 扩散系数与扩散时间关系曲线 Fig. 7 Relationship between diffusion coefficient and diffusion time |
Zhang等人[4]基于菲克定律,应用半无限边界条件,得出扩散过程中压力P和时间t的关系式为:


图 8是实验过程中采集到的压力衰减数据,应用Oringin软件对压力衰减数据进行双指数拟合,可得到k1和k2的值,然后取较大者为k*,这里k* = 22 344.9,结合已知液面高度20 mm,可由(10)式计算得出平衡时间为50 640 s情况下的整体平均扩散系数为7.3×10-9 m2/s.

|
| 图 8 扩散过程的压力衰减曲线 Fig. 8 Pressure decay records during the diffusion processes |
应用图 7中得到的拟合式,用Matlab软件编程应用梯形法则,分别计算扩散时间为80 min,144 min,240 min,400 min,600 min,844 min情况下的整体平均扩散系数,与应用PVT法拟合相应扩散时间的压力衰减曲线,然后由(10)式求得的整体平均扩散系数相比较,两种方法的误差在2.7%~22.3%之间,结果如表 1所示.从表中可发现,整体平均扩散系数随着扩散时间的增加而降低,这是因为随着扩散的进行,CO2浓度梯度降低,导致整体平均扩散系数降低.由MRI法测得平衡时间844 min(50 640 s)内的整体平均扩散系数为7.1×10-9 m2/s,与PVT法测的结论7.3×10-9 m2/s相比较,误差为2.7%.与相似实验条件下,Wang等人[17](3.32~5.71×10-9 m2/s)、Grogan等人[18] (1.80~ 3.21×10-9 m2/s)的实验结论具有相同的数量级(10-9 m2/s).
| 扩散系数 /(10-9m2/s) | Time/min | 80 | 144 | 240 | 400 | 600 | 844 |
| MRI法 | 77.8 | 48.2 | 25.1 | 15.3 | 11.5 | 7.1 | |
| 压力衰减法 | 100.1 | 57.1 | 30.3 | 19.5 | 14.3 | 7.3 | |
| 相对误差/% | 22.3 | 15.6 | 17.2 | 21.5 | 19.6 | 2.7 |
测试过程中MRI的参数、样品位置、温度均是不变的,CO2的浓度数据是通过信号强度进行比值处理后得到的,相应的参数影响被抵消,扩散系数由CO2的浓度数据计算得出的,因此可以认为实验参数等其它参数对MRI测得的扩散系数的影响是可以抵消的.
3 结论MRI技术是研究气体扩散过程的有效工具,对MRI图像进行信号强度分析,应用有限体积分析法不仅能对扩散过程进行分析,还能得出任意扩散时间范围的整体平均扩散系数,将MRI方法得出的扩散平衡时间范围内的整体平均扩散系数与PVT法相比较,误差为2.7%,并且与前人相似条件下的实验结论具有相同的数量级(10-9),说明该实验所采取的工具和分析方法是可靠的,并且根据实验结果得出以下结论:
(1) 扩散系数沿扩散方向降低,随扩散时间以指数形式下降;
(2) 整体平均扩散系数随扩散时间的增加而减小.
| [1] | Abedini A, Torabi F. On the CO2 storage potential of cyclic CO2 injection process for enhanced oil recovery[J]. Fuel, 2014, 124: 14-27. |
| [2] | Kavousia S, Farshid T, Chanb C W, et al. Experimental measurement and parametric study of CO2 solubility and molecular diffusivity in heavy crude oil systems[J]. Fluid Phase Equilibr, 2014, 371: 57-66. |
| [3] | Riazi M R. A new method for experimental measurement of diffusion coefficients in reservoir fluids[J]. J Petrol Sci Eng, 1996, 14: 235-250. |
| [4] | Zhang Y P, Hyndman C L, Maini B B. Measurement of gas diffusivity in heavy oils[J]. J Petrol Sci Eng, 2000, 25: 37-47. |
| [5] | Davis P K, Lundy G D, Palamara J E, et al. New pressure decay techniques to study gas sorption and diffusion in polymers at elevated pressures[J]. Ind Eng Chem Res, 2004, 43: 1537-1542. |
| [6] | Wen Y W, Kantzas A. Monitoring Bitumen-solvent interactions with low-field nuclear magnetic resonance and X-ray computer-assisted tomography[J]. Energy & Fuels, 2005, 19: 1319-1326. |
| [7] | Song L, Kantzas A, Bryan J, et al. Experimental Measurement of Diffusion Coefficient of CO2 in Heavy Oil Using X-Ray Computed-Assisted Tomography Under Reservoir Conditions[C]. Canada: The Canadian Unconventional Resources & International Petroleum Conference, Society of Petroleum Engineers, 2010, CSUG/SPE 137545. |
| [8] | Araujo S V, Vargas J A V, Trevisan O V. Diffusion Coefficient of CO2 in Light Oil Under Reservoir Conditions Using X-Ray Computed Tomography[C]. Brazil: Offshore Technology Conference, 2013, OTC 24454. |
| [9] | Song L, Kantzas A, Bryan J. Investigation of CO2 Diffusivity in Heavy Oil Using X-Ray Computer-Assisted Tomography Under Reservoir Conditions[C]. USA: International Conference on CO2 Capture, Storage, and Utilization, Society of Petroleum Engineers, 2010, SPE138205. |
| [10] | Zhang Zong-fu(张宗富), Xiao Li-zhi(肖立志), Liu Hua-bing(刘化冰), et al. Simulation of restricted diffusion of water molecules in mieropores(水分子在微孔隙介质中的受限扩散模拟)[J]. Chinese J Magn Reson(波谱学杂志), 2014, 31(1): 49-60. |
| [11] | Li Xin-jun(李新军), Nie Sheng-dong(聂生东), Wang Yuan-jun(王远军), et al. An improved two-dimensional inversion algorithm for low-field NMR diffusion-transverse relaxation correlation data(低场核磁共振扩散-横向弛豫二维反演算法)[J]. Chinese J Magn Reson(波谱学杂志), 2013, 30(3): 322-335. |
| [12] | Ersland G, husebo J, Graue A, et al. Measuring gas hydrate formation and exchange with CO2 in Bentheim sandstone using MRI tomography[J]. Chem Eng J, 2010, 158: 25-31. |
| [13] | Liu Y, Zhao Y, Zhao J, et al. Magnetic resonance imaging on CO2 miscible and immiscible displacement in oil-saturated glass beads pack[J]. Magn Reson Imaging, 2011, 29: 1110-1118. |
| [14] | Zhao Y C, Song Y C. Visualization of CO2 and oil immiscible and miscible flow processes in porous media using NMR micro-imaging[J]. Petrol Sci, 2011, 8: 183-193. |
| [15] | Guerrero A U, Kantzas A. Diffusion of Hydrocarbon Gases in Heavy Oil and Bitumen[C]. Colombia: The 2009 SPE Latin American and Caribbean Petroleum Engineering Conference held in Cartagena, SPE 1222783. |
| [16] | Jamialahmadi M, Emadi M. Diffusion coefficients of methane in liquid hydrocarbons at high pressure and temperature[J]. J Petrol Sci Eng, 2006, 53: 47-60. |
| [17] | Wang L S, Lang Z X, Guo T M. Measurement and correlation of the diffusion coefficients of carbon dioxide in liquid hydrocarbons under elevated pressures[J]. Fluid Phase Equilibr, 1996, 117(1, 2): 364-372. |
| [18] | Grogan A T, Pinczewski V W, Ruskauff G J, et al. Diffusion of CO2 at reservoir conditions: models and measurements[J]. Spe Reservoir Eng, 1988, 3(1): 93-102. |
 2015, Vol. 32
2015, Vol. 32