文章信息
- 董芳,王前锋,郑慧,李智敏,杨光,李建奇
- DONG Fang, WANG Qian-feng, ZHENG Hui, LI Zhi-ming, YANG Guang, LI Jian-qi
- 结合导航回波与压缩感知进行运动伪影矫正
- Motion Artifacts Correction in MRI with Navigator Echo Combined with Compressed Sensing
- 波谱学杂志, 2015, 32(3): 419-429
- Chinese Journal of Magnetic Resonance, 2015, 32(3): 419-429
- http://dx.doi.org/10.11938/cjmr20150303
-
文章历史
- 收稿日期:2014-08-28
- 收修改稿日期:2015-07-23
运动是磁共振成像中最常见的问题,由运动导致的伪影会降低磁共振图像的质量,严重影响临床医生做出正确诊断.导航回波技术是一种广泛应用于监测成像物体运动和伪影矫正的技术[1, 2, 3].在一定幅度范围内,导航回波可有效追踪物体的运动,如呼吸运动、小幅度头部运动等[4, 5, 6, 7],并可利用监测得到的运动信息对k空间数据进行矫正[7, 8],从而降低运动伪影对图像质量的影响.然而导航回波技术无法很好地矫正大幅度运动以及非刚体运动导致的图像伪影,往往使得运动时刻采集到的k空间数据只能舍弃.
压缩感知(Compressed Sensing,CS),也称压缩传感或压缩采样[9, 10],通过非线性重建算法,在远小于Nyquist采样率的条件下,对欠采样的数据进行重建恢复出原始信号.应用压缩感知进行图像重建需要满足两个重要条件[11]:(1) 所要重建的图像能变换到一种稀疏形式;(2) k空间数据必须为随机欠采样,其经傅立叶变换后,图像中的伪影如噪声一般是非相干的.磁共振图像能很好地满足这两个条件,因此可以将压缩感知技术应用于磁共振成像领域[12, 13].近年来,压缩感知已广泛地应用于磁共振成像领域,对随机欠采样的数据进行重建,以缩短成像时间[12, 13, 14, 15].Barral小组提出结合压缩感知和导航回波技术进行运动伪影矫正[16],但他们只是针对运动之后回到原来位置的情况进行了矫正,这在实际的应用中有很大的局限性,因为被试在运动之后很难回到初始位置.
本文报道了一种结合导航回波与压缩感知进行运动伪影矫正的方法,其在常规梯度回波序列中整合导航回波用以监测人体运动,并采用特定的相位编码顺序以伪随机的方式进行数据采集,重建时舍弃受运动影响的数据,并采用压缩感知方法对未受运动影响的部分数据进行图像重建.对运动的颅脑和膝关节的扫描实验表明:该矫正方法对被试任意的一次运动均有较好的矫正效果,能明显去除或减少图像中的运动伪影.
1 材料和方法1例男性健康志愿者参与该项研究.所有扫描均在西门子3 T磁共振成像设备(MAGNETOM Trio a Tim)上完成,系统软件版本为syngo MR VB17.头部扫描采用大体线圈作为信号发射线圈,采用12通道头线圈作为信号接收线圈.膝关节扫描采用膝关节线圈作为信号发射和接收线圈.数据后处理均在MATLAB 7.11.0(R2010b)上完成.
1.1 脉冲序列的实现集成有导航回波的二维和三维梯度回波序列于西门子公司的序列集成开发平台IDEA上开发实现.三维梯度脉冲时序图如图 1所示.第二个回波作为导航回波,选层方向上和相位编码方向上的相位编码梯度的作用已被相应的反向梯度抵消[5].该回波为一维导航回波,用于探测物体的运动.该序列中,选层方向上和相位编码方向上的相位编码是伪随机方式[17].二维梯度回波序列在选层方向上不加相位编码.
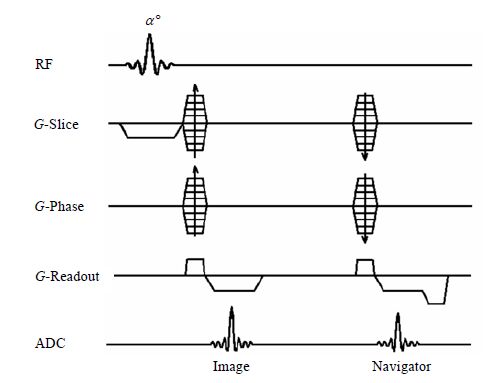
|
| 图 1 集成有导航回波的三维梯度回波脉冲序列时序图 Fig. 1 Schematic of 3D gradient echo sequence with an additional navigator echo |
将欠采样的k空间数据进行反傅立叶变换,由欠采样引入的伪影像噪声一样,是随机分布的.为满足非相干性,需进行随机欠采样,且随机性越高,伪影的非相干性越好,重建的效果也越好[13].在磁共振成像中,k空间中心附近的数据决定了图像的对比度和信噪比,因此可考虑用k空间中心附近数据全采,其他数据随机欠采的方式,以得到一个伪随机欠采的k空间数据.
若要得到该伪随机欠采的k空间数据,需对相位编码梯度施加顺序进行特殊设计.在二维图像采集中,相位编码梯度施加顺序如图 2(a)所示,该序列中有两次k空间中心30行数据的采集,分别在扫描开始与结尾时进行,其他的相位编码梯度施加顺序随机排列.在扫描开始时,序列未达到稳态,此时若采集k空间中心数据,会对图像产生较大影响[16],因此可将该处的k空间中心数据延后采集.在三维图像采集中,选层方向及相位编码方向上需要同时进行随机采集,两个方向上的相位编码梯度施加方式如图 2(b)所示.该序列中有两次k空间中心32×32行数据的采集,分别在扫描开始与结尾时进行.用这两个序列对图像进行扫描,得到相应的k空间数据,根据运动的分布时刻,选择未受运动影响的数据较多的一部分进行压缩感知重建.

|
| 图 2 相位编码梯度施加顺序.(a) 二维成像中的相位编码梯度施加顺序,相位编码数Ny = 256;(b) 三维成像中的相位编码梯度施加顺序,相位编码数为136×128(相位编码方向上的相位编码数Ny × 层方向上的相位编码数Nz) Fig. 2 The orders of phase encoding gradient in 2D imaging (a) and 3D imaging (b). The number of phase encoding is 256 for 2D imaging. The number of phase encoding is 136×128 (number of phase encoding in phase encoding direction × number of phase encoding in slice direction) for 3D imaging |
二维梯度回波的扫描参数设置为:重复时间(TR) = 250 ms,图像回波的回波时间(TE)为4.8 ms,导航回波的TE为11 ms,翻转角(FA) = 70°,视野(FOV) = 250 mm×250 mm(频率编码×相位编码),层厚(slice thickness) = 5 mm,层数(slice) = 1,带宽(bandwidth) = 330 Hz/pixel,扫描矩阵(matrix) = 256×286(频率编码×相位编码),扫描方向为横断面,相位编码方向为左右方向,扫描时间为1 min 12 s.用该序列对被试的颅脑进行3次扫描,要求被试在每次扫描中进行一次大幅度头部运动,持续时间在10 s左右,头动时间点分别为扫描开始时、扫描结束时和一次扫描中间随机时间.最后在被试保持静止时再进行一次采集,作为对照.
三维梯度回波的扫描参数设置为:TR = 30 ms,图像回波的TE为4.8 ms,导航回波的TE为11 ms,FA = 15°,FOV = 256 mm×128 mm(频率编码×相位编码),slice thickness = 1 mm,层数(slice per slab) = 128,bandwidth = 390 Hz/pixel,matrix = 256×136(频率编码×相位编码),扫描方向为矢状面,相位编码方向为前后方向,扫描时间为 8 min 42 s.用该序列对被试的膝关节进行3次扫描,要求被试在每次扫描中进行一次大幅度膝关节运动,在膝关节线圈允许的范围内运动,持续时间在1 min左右,运动时间点分别为扫描开始时、扫描结束时和一次扫描中间随机时间.最后在被试保持静止时再进行一次采集,作为对照.
1.4 数据处理和分析图像重建流程图如图 3所示:图 3(a)为图像重建的流程框架,图 3(b)为压缩感知重建中的整个迭代过程.首先,将扫描后得到的原始数据分为图像回波数据和导航回波数据两部分;然后,利用导航回波数据得到采集数据时被试的运动信息,结合相位编码梯度的施加顺序获得相应的欠采样模板;接着,图像回波的原始k空间数据根据采样模板生成欠采样k空间数据(舍弃被运动破坏的相关原始数据);该k空间数据经过反傅立叶变换后,得到欠采样图像,欠采样图像经过小波变换后得到小波系数,通过最优化方法,利用目标函数值的变化情况修改小波系数;其次小波系数经过反小波变换后获得新图像,进行傅立叶变换后得到新的k空间数据,用同一个采样模板对该数据进行欠采样,得到新的欠采样k空间数据,与真实的k空间数据进行数据保真判定.然后根据稀疏项与保真项计算新的目标函数(也叫能量函数E0).若能量函数减小,则将该能量函数作为新的能量函数,进行下一次迭代,直到能量函数变化量小于某个阈值或是达到设定的迭代次数后跳出循环[12, 13, 14].最后,将所有通道重建后的图像采用均方根的方式进行多通道组合,获得最终矫正后的图像.其中主要重建参数如下:迭代次数=3*8,TV惩罚项权重=0.002,L1范数惩罚项权重=0.005.
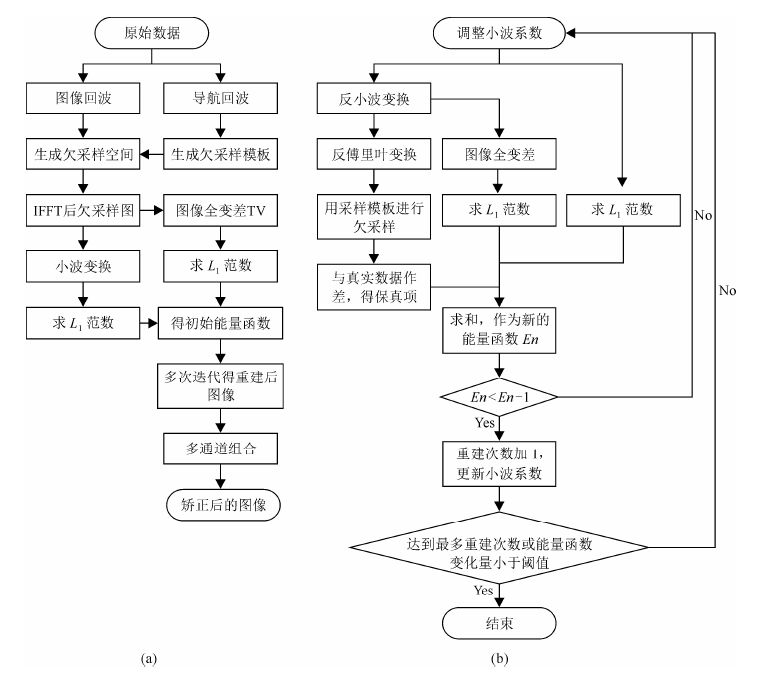
|
| 图 3 图像重建流程图.(a) 图像重建的流程框架;(b) 压缩感知重建中的整个迭代过程 Fig. 3 Diagram of image reconstruction process. (a) the frame of image reconstruction; (b) the iteration of compressed sensing |
图 4为二维图像进行压缩感知重建时的图.图 4(a)即为结合运动信息及相位编码梯度施加顺序得到的采样模板,为256×256的矩阵.kx方向为频率编码方向,为全采;ky方向为相位编码方向,为欠采.其中黑色代表0,对应于k空间受运动影响的数据,重建时将被舍弃;白色代表1,对应于k空间未受运动影响的数据,将用于图像重建.图像回波的原始k空间数据乘以采样模板得到欠采样k空间数据,如图 4(b)所示,此时的k空间数据都未受到运动影响.对欠采样k空间数据进行反傅立叶变换,得到欠采样图像,对该图像进行小波变换,得到小波系数,图 4(c)中可看到有明显伪影的小波系数.通过最优化方法,修改小波系数,经过多次迭代,最终得到一个合适的解,图 4(d)是多次迭代后的小波系数,可看到伪影已大幅减少.用该小波系数进行反小波变换,获得矫正后的颅脑图.

|
| 图 4 二维图像进行压缩感知重建时的图.(a) 欠采样模板;(b) 欠采样k空间;(c) 欠采样图像的小波域;(d) 重建图像的小波域 Fig. 4 2D images during reconstruction of compressed sensing. (a) undersampled mask; (b) undersampled k-space data; (c) wavelet domain of undersampled image; (d) wavelet domain of reconstructed image |
图 5是健康志愿者由导航回波检测到的头部运动情况及矫正前后的颅脑图.图 5左侧为3次扫描中导航回波的相位与幅度值随相位编码步数的变化图,虚线框内为被试运动时相应的相位与幅度值的波动情况,可见导航回波能准确地监测到被试的运动信息.图 5右侧为相应3种状态下得到的矫正前后的颅脑图,其中矫正前的颅脑图是采用原始k空间图像变换得到.图 5(d)为静止时采集到的图像,作为对照图.由图可知:矫正前,运动导致图像产生严重的伪影,灰白质界面不清,严重影响医学诊断;通过导航回波监测运动并结合压缩感知技术进行图像重建,矫正后,可看到伪影得到了很好的消除,同时灰白质分界清晰,很好地显示了颅脑的细微结构.与对照图 5(d)相比,矫正后的图像均得到了较好的复原.

|
| 图 5 导航回波的相位与幅度值随相位编码步数的变化图及对应的矫正前后的颅脑图.(a) 扫描前期头动;(b) 扫描后期头动;(c) 随机一次头动;(d) 对照图 Fig. 5 The diagram of phase and magnitude of navigator echo during scanning and brain images before and after correction. (a) head movement at the beginning of scanning; (b) head movement at the end of scanning; (c) head movement randomly; (d) reference image |
图 5(a)和图 5(b)分别为扫描开始时头动和扫描结束时头动,根据导航回波的信息,用于压缩感知重建的相位编码分别取70~286和11~230,欠采率分别为15.2%和14.1%,重建效果非常理想.图 5(c)是随机的一次头动后得到的图,运动前后的数据虽然都是静止时采集得到,但两个静止状态的位置并不相同,因此不能将两部分数据同时用于重建,而是取了数据量相对较多的部分进行重建,重建的相位编码取111~286,欠采率为31.3%,因此重建效果相对于前两种情况较差,但比矫正前的图像大有改善,运动伪影得到了很好的抑制,图像具有较好的医学诊断价值.
2.2 三维图像运动伪影矫正结果图 6为三维图像进行压缩感知重建时的图.图 6(a)为结合运动信息及相位编码梯度施加顺序得到的采样模板.kx方向为频率编码方向,为全采;ky方向为相位编码方向,kz方向为选层方向,均为欠采.其中黑色代表0,对应于k空间需要被舍弃的数据;白色代表1,表示用于图像重建的数据,采样模板为128×128的矩阵.在三维图像的数据处理中,需要首先在频率编码方向上进行一维傅立叶变换,然后对该方向上每层的k空间使用同一个采样模板,原始k空间数据在采样模板作用下得到欠采样k空间数据.

|
| 图 6 三维图像进行压缩感知重建时的图.(a) 欠采样模板;(b) 欠采样的k空间;(c) 欠采样图像的小波域;(d) 重建图像的小波域 Fig. 6 3D images during reconstruction of compressed sensing. (a) undersampled mask; (b) undersampled k-space data; (c) wavelet domain of undersampled image; (d) wavelet domain of reconstructed image |
图 6(b)为其中一层的欠采样k空间数据.三维图像的压缩感知重建过程与二维图像的处理过程类似[14],但需对每一层都进行图像重建,因此重建时间较长,其与需要重建的层数成正比.结合实际需求与图像重建时间,此处取频率编码方向上的中间128层进行图像重建.图 6(c)是其中一层迭代前的小波系数,可看到类似噪声的伪影;图 6(d)是多次迭代后的小波系数,伪影大幅减少,用该小波系数进行反小波变换,获得该层矫正后的膝关节横断面图.
图 7是健康志愿者由导航回波检测到的运动情况及矫正前后的膝关节图,分别显示了三维图像的横断面、冠状面与矢状面.图 7左侧为3次扫描中导航回波的相位与幅度值随相位编码步数的变化图,虚线框内为被试运动时相应的相位与幅度值的波动情况,可见导航回波能准确地监测到被试的运动信息.图 7右侧为相应3种状态下得到的矫正前后的膝关节图,其中矫正前的膝关节图是采用原始k空间图像变换得到.图 7(d)为静止时采集到的图像,作为对照图.由图可知:矫正前,有明显的类似噪声的伪影,尤其在横断面上,图像的细节被掩盖,肌肉组织粗糙,组织结构分界模糊,严重影响了图像的对比度与分辨率,很容易掩盖小的病灶,影响医学诊断;通过导航回波监测运动并结合压缩感知技术进行图像重建矫正后,伪影得到了明显的抑制,组织结构间分界清晰,肌肉组织平滑,细节分明.与对照 图 7(d)相比,3种情况下,矫正后的图像均获得了较好的复原.
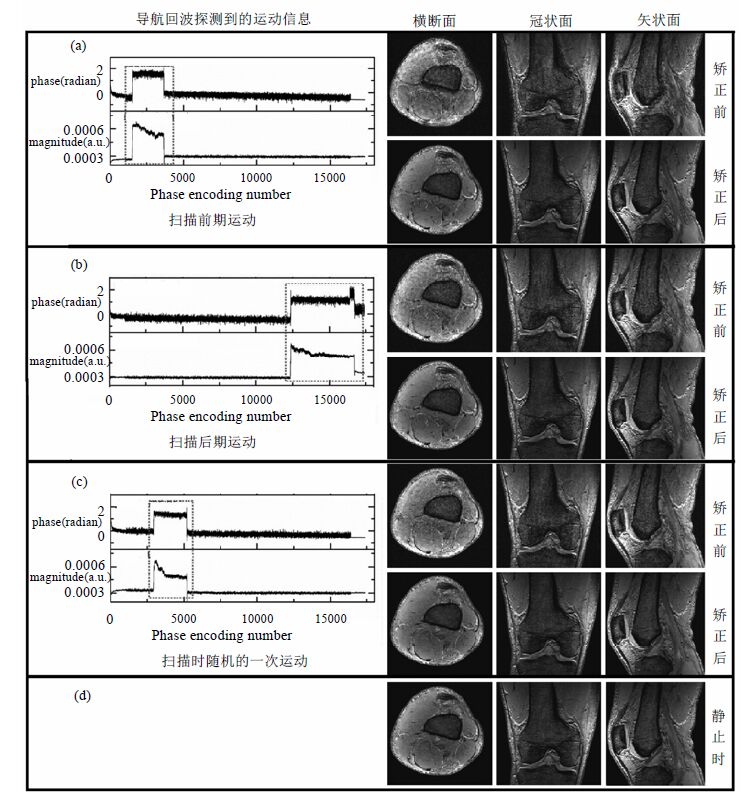
|
| 图 7 导航回波的相位与幅度值随相位编码步数的变化图及对应的矫正前后的膝关节图.(a) 扫描前期运动;(b) 扫描后期运动;(c) 随机一次运动;(d) 对照图 Fig. 7 The diagram of phase and magnitude of navigator echo during scanning and knee images before and after correction. (a) knee movement at the beginning of the scanning; (b) knee movement at the end of the scanning; (c) knee movement randomly; (d) reference image |
本文主要报道了结合导航回波与压缩感知进行运动伪影矫正,该矫正方法对扫描过程中有一次大幅运动或非刚体运动均有很好的矫正效果.与Barral小组提出的矫正方 法[16]相比,该方法并不需要被试在运动完之后回到初始位置(多次实验也发现被试很难再回到初始位置).本文报道的矫正方法的优点是,运动的激烈程度,运动方向及非刚体运动均会使采集到的数据受到不同程度的影响,导航回波探测到受运动影响的数据后,这些数据将被舍弃,不再用于图像重建.因此,运动形式及运动幅度的大小均不会影响该算法的鲁棒性.然而,该矫正方法中用于图像重建的数据必须包含k空间中心附近的数据,然后再选择未受运动影响的数据进行重建.其中用于图像重建的数据量越大,重建效果越好.因此该方法仍有一定的局限性,运动的时间点及运动的频率会严重影响该算法的鲁棒性,该算法适用于在采集过程中某个集中的时间段内有一次或几次不同程度的运动.若扫描前期与后期都发生运动,即两次的k空间中心数据采集时均受到运动影响,则图像运动伪影难以得到较好的矫正.在今后的工作中,可对相位编码的排序做进一步优化,或尝试与半傅里叶变换法结合,以提高该方法的重建效果.
3 结论磁共振成像中成像物体的运动,尤其是大幅运动引起的运动伪影很难进行矫正[5, 6],只能重新采集所有数据,这将对病人及扫描员带来时间的浪费.本文对相位编码梯度的施加顺序进行特定的设计,并利用导航回波监控病人的运动情况,重建时舍弃被运动破坏的相关原始数据,然后利用未受运动影响的伪随机欠采样数据,进行压缩感知重建,较好地恢复出原始图像.该方法对二维和三维磁共振成像均适用,这为运动伪影的矫正提供了一种新思路.
| [1] | Miller K L, Pauly J M. Nonlinear phase correction for navigated diffusion imaging[J]. Magn Reson Med, 2003, 50(2): 343-353. |
| [2] | Mori S, Van Zijl P C. A motion correction scheme by twin-echo navigation for diffusion-weighted magnetic resonance imaging with multiple RF echo acquisition[J]. Magn Reson Med, 1998, 40(4): 511-516. |
| [3] | Fu Z W, Wang Y, Grimm R C, et al. Orbital navigator echoes for motion measurements in magnetic resonance imaging[J]. Magn Reson Med, 1995, 34(5): 746-753. |
| [4] | Hu X, Kim S G. Reduction of signal fluctuation in functional MRI using navigator echoes[J]. Magn Reson Med, 1994, 31(5): 495-503. |
| [5] | Wang Qian-feng(王前锋), Li Jian-qi(李建奇), Wu Dong-mei(吴东梅), et al. Implementation of high resolution diffusion weighted imaging of small animal in clinical MRI system(小动物高分辨扩散加权成像在临床MRI上的实现)[J]. Chinese J Magn Reson(波谱学杂志), 2012, 29(3): 372-378. |
| [6] | Dong Fang(董芳), Pei Meng-chao(裴梦超), Wang Qian-feng(王前锋), et al. Gradient echo imaging of the human brain: respiratory induced artifacts and navigator echo correction(颅脑梯度回波成像:呼吸伪影和导航回波矫正)[J]. Chinese J Magn Reson(波谱学杂志), 2014, 31(3): 321-330. |
| [7] | van der Kouwe A J, Benner T, Dale A M. Real-time rigid body motion correction and shimming using cloverleaf navigators[J]. Magn Reson Med, 2006, 56(5): 1 019-1 032. |
| [8] | Anderson A W, Gore J G. Analysis and correction of motion artifacts in diffusion-weighted imaging[J]. Magn Reson Med, 1994, 32(2): 379-387. |
| [9] | Donoho D L, Compressed sensing[J]. IEEE T Inform Theor, 2006, 52(4): 1 289-1 306. |
| [10] | Candès E, Romberg J. Sparsity and incoherence in compressive sampling[J]. Inverse Prob, 2007, 23(3): 969-985. |
| [11] | Candès E, Wakin M. An introduction to compressive sampling[J]. IEEE Signal Proc Mag, 2008, 25(2): 21-30. |
| [12] | Lustig M, Donoho D, Pauly J M. Sparse MRI: The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med, 2007, 58(6): 1 182-1 195. |
| [13] | Lustig M, Donoho D L, Santos J M, et al. Compressed sensing MRI[J]. IEEE Signal Proc Mag, 2008, 25(2): 72-78. |
| [14] | Gao Ming-sheng(高明生), Xie Hai-bin(谢海滨), Yan Xu(严序), et al. Selective dual-direction sequenential compressed sensing for dynamic MR imaging(用于动态磁共振成像的选择性双向顺序压缩感知重建)[J]. Chinese J Magn Reson(波谱学杂志), 2013, 30(2): 194-203. |
| [15] | Liang D, DiBella E V R, Chen R R, et al. K-t ISD: Dynamic cardiac MR imaging using compressed sensing with iterative support detection[J]. Magn Reson Med, 2012, 68(1): 41-53. |
| [16] | Barral J K, Nishimura D G. Compressed Sensing for Motion Artifact Reduction[C]. Proc Intl Soc Mag Reson Med, 2009, 17(4): 4 593. |
| [17] | Haldar J P, Hernando D, Liang Z P. Compressed-sensing MRI with random encoding[J]. IEEE T Inform Theor, 2011, 30(4): 893-903. |
 2015, Vol. 32
2015, Vol. 32




