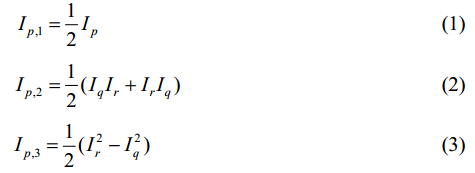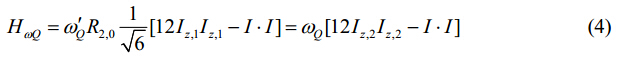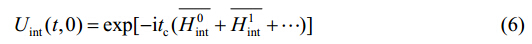文章信息
- 沈明,ROOPCHAND Rabia,MANANGA Eugene S,慕松柏,陈群,BOUTIS Gregory S,胡炳文
- SHEN Ming, ROOPCHAND Rabia, MANANGA Eugene S, AMOUREUX Jean-paul, CHEN Qun, BOUTIS Gregory S, HU Bing-wen
- 组合脉冲宽带激发2H-平均哈密顿理论计算研究
- Theoretical Calculation of a Composite Pulse with 8-Step Phase Cycling for 2H Broadband Excitation by Average Hamiltonian Theory
- 波谱学杂志, 2015, 32(2): 373-381
- Chinese Journal of Magnetic Resonance, 2015, 32(2): 373-381
- http://dx.doi.org/10.11938/cjmr20150219
-
文章历史
- 收稿日期:2015-01-30
- 收修改稿日期:2015-05-16
2. Department of Physics, Hunter College, New York 10065;
3. Center for Advanced Radiological Sciences, Division of Nuclear Medicine and Molecular Imaging Physics, Department of Radiology, Harvard Medical School and Massachusetts General Hospital, Boston, 02114;
4. Physics Department, Brooklyn College, New York 11210;
5. UCCS, University Lille North of France, Villeneuve d'Ascq 59652
2. Department of Physics, Hunter College, New York 10065;
3. Center for Advanced Radiological Sciences, Division of Nuclear Medicine and Molecular Imaging Physics, Department of Radiology, Harvard Medical School and Massachusetts General Hospital, Boston, 02114;
4. Physics Department, Brooklyn College, New York NY 11210;
5. UCCS, University Lille North of France, Villeneuve d'Ascq 59652
In solid-state Nuclear Magnetic Resonance (SSNMR), deuterium quadrupolar echo spectroscopy is a powerful tool for investigating structure and dynamics. Quadrupolar coupling parameters extracted from static 2H powder patterns enable the study of dynamics, hydrogen bonding, ligand identification and chemical exchange in a variety of systems[1, 2, 3]. The wide range of applications of quadrupolar echo spectroscopy has also driven methodology development for many years[4, 5, 6, 7, 8, 9].
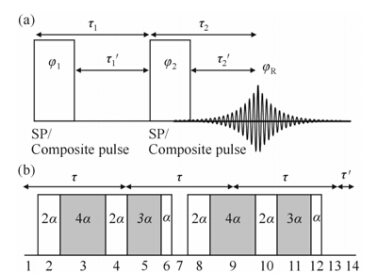
Although the quadrupolar coupling of spin-1 2H nuclei is far smaller than those of most half-integer spins, the strength (typically in the range of CQ = e2qQ = 50-180 kHz[10, 11]) is comparable with the maximum RF field strength that can be achieved by modern NMR probes. To uniformly excite the wide spectral widths, quadrupolar echo method [Fig. 1(a)] based on composite pulses [Fig. 1(b)] with 8-step phase cycling (Table 1) has been developed[12]. It was reported that finite pulse width effect could be partially removed by using 8-step phase cycling[13]. It was shown that COM-II with an 8-step phase cycling could reduce the requisite RF fields for uniform excitation, and thus yield undistorted spectra for accurate line-shape measurements. The performance of COM-II was slightly better than COM-IV, in particular in the outer edges of the quadrupolar echo spectra, as evidenced by our recent simulation work (see figure 2 of ref. [12]) and we chose to analyze COM-II in this work.
| Step | φ1 | φ2 | φR |
| 1 | x | y | -y |
| 2 | x | -y | -y |
| 3 | -x | y | y |
| 4 | -x | -y | y |
| 5 | y | x | x |
| 6 | y | -x | x |
| 7 | -y | x | -x |
| 8 | -y | -x | -x |
|
| Fig. 1 (a) Pulse sequence of 2H quadrupole echo experiment. The echo is formed at τ2′ after the second 90° pulse due to finite pulse width effect. (b) COM-II pulse, white rectangles denotes pulses with 0° phase, filled rectangles denotes pulses with a 180° phase shift. The cycle shown here corresponds to the first row in Table 1. 2a corresponds to the length of 90° pulse |
In this paper, we report an analysis of COM-II with an 8-step phase cycle for quadrupolar echo spectroscopy by average Hamiltonian theory. Analytical results, to first order of the Magnus expansion, highlight the performance of this composite pulse with an 8-step phase cycling scheme. By applying the fictitious spin-1 operators, this work highlights the mechanism of the 8-step phase cycling that minimizes spectral distortions. 1 Analytical calculations of COM-II
The quadrupolar echo pulse sequence is shown in Fig. 1(a). The quadrupolar interaction is refocused by two 90° single pulses or composite pulses and an echo is formed at time after the second 90° pulse (t2′ in Fig. 1). In this pulse sequence, the nuclear spins evolve under both the RF and quadrupolar interaction. Large quadrupolar interactions comparable to the RF field lead to a distorted echo occurring at t2′ rather than t2′. In addition, as we show below, spectral distortions arise from the composite evolution of the spins under both the RF and internal Hamiltonians. In practice, the free induction decay (FID) is sampled before the echo peak and is left shifted in order to place the first data point at the peak of the echo before Fourier transformation.
Below we provide analytical results, based on average Hamiltonian theory[14] and focus the discussion on COM-II which provided the highest performance amongst the composite pulses we investigated[12]. In this treatment, we take only the first order quadrupolar interactions and ignore the chemical shift anisotropy and dipolar interactions. Further, in our analysis, we make use of the fictitious spin-1 operators[15]which are defined as
with p = x, y, z and (p, q, r) = (x, y, z) with cyclic permutations. In this formalism, the Hamiltonian of the quadrupolar interaction in the principal axis frame may be written as
In the above expressions, R2, 0is given by ${R_{2, 0}} = \sqrt {\frac{3}{2}} \{ {P_2}[\cos (\theta )] + \frac{\eta }{2}\cos (2\theta ){\sin ^2}(\varphi )\} $ and the constant ${\omega '_Q} = \frac{{{e^2}qQ}}{{2I(2I - 1)h}}$. Therefore, ${\omega _Q}$ is given by ${\omega _Q} = \frac{{{e^2}qQ}}{{4I(2I - 1)h}}\{ {P_2}[\cos (\theta )] + $$\frac{\eta }{2}\cos (2\theta ){\sin ^2}(\varphi )\} $. ${P_2}[\cos (\theta )]$is the second-order Legendre polynomial of cos(q), qand jare two of the three Euler angles.
In the average Hamiltonian treatment[14] the density matrix at a given time tc, termed a cycle, may be evaluated as
where the propagator${U_{{\rm{RF}}}}$ is given by the Dyson series and ${U_{{\rm{int}}}}$ is given by the Magnus expansion
In what follows we restrict the discussions to the leading order term in the Magnus expansion which is given by
Table 2 provides the integrated toggling frame Hamiltonians for sequence COM-II, and Table 3 highlights the average Hamiltonians for all combinations of the COM-II quadrupolar echo sequence. Here we restricted the computations of spin state at 3τ. A schematic of the composite pulse is provided in Fig. 1(b) with the various durations denoted as δn (n = 1∶14). In our parameterization, the entire pulse sequence is of duration T = 3τ and a 90° pulse width has duration 2a.
| Interval | Time | ${\overline H _{{\omega _Q}}}$ |
| δ1 | $0 \le t \le \tau - 8\alpha $ | $\frac{{{\omega _Q}}}{T}(12{I_{z, 1}}{I_{z, 1}} - I \cdot I)(\tau - 8\alpha )$ |
| δ2 | $\tau - 8\alpha \le t \le \tau - 6\alpha $ | $\frac{{2\alpha {\omega _Q}}}{T}[6{I_{z, 1}}{I_{z, 1}} + 6{I_{x, 1}}{I_{x, 1}} + \frac{{12}}{\pi }({I_{z, 1}}{I_{x, 1}} + {I_{x, 1}}{I_{z, 1}}) - I \cdot I]$ |
| δ3 | $\tau - 6\alpha \le t \le \tau - 2\alpha $ | $\frac{{4\alpha {\omega _Q}}}{T}(6{I_{z, 1}}{I_{z, 1}} + 6{I_{x, 1}}{I_{x, 1}} - I \cdot I)$ |
| δ4 | $tau - 2\alpha \le t \le \tau $ | $\frac{{2\alpha {\omega _Q}}}{T}[6{I_{z, 1}}{I_{z, 1}} + 6{I_{x, 1}}{I_{x, 1}} - \frac{{12}}{\pi }({I_{z, 1}}{I_{x, 1}} + {I_{x, 1}}{I_{z, 1}}) - I \cdot I]$ |
| δ5 | $\tau \le t \le \tau + 3\alpha $ | $\frac{{3\alpha {\omega _Q}}}{T}[(6 - \frac{4}{\pi }){I_{z, 1}}{I_{z, 1}} + (6 + \frac{4}{\pi }){I_{x, 1}}{I_{x, 1}} - \frac{4}{\pi }({I_{z, 1}}{I_{x, 1}} + {I_{x, 1}}{I_{z, 1}}) - I \cdot I]$ |
| δ6 | $\tau + 3\alpha \le t \le \tau + 4\alpha $ | $\frac{{\alpha {\omega _Q}}}{T}[(6 - \frac{{12}}{\pi }){I_{z, 1}}{I_{z, 1}} + (6 + \frac{{12}}{\pi }){I_{x, 1}}{I_{x, 1}} + \frac{{12}}{\pi }({I_{x, 1}}{I_{z, 1}} + {I_{z, 1}}{I_{x, 1}}) - I \cdot I]$ |
| δ7 | $\tau + 4\alpha \le t \le 2\tau - 4\alpha $ | $\frac{{{\omega _Q}}}{T}(12{I_{x, 1}}{I_{x, 1}} - I \cdot I)(\tau - 8\alpha )$ |
| δ8 | $2\tau - 4\alpha \le t \le 2\tau - 2\alpha $ | $\frac{{2\alpha {\omega _Q}}}{T}[6{I_{x, 1}}{I_{x, 1}} + 6{I_{y, 1}}{I_{y, 1}} + \frac{{12}}{\pi }({I_{x, 1}}{I_{y, 1}} + {I_{y, 1}}{I_{x, 1}}) - I \cdot I]$ |
| δ9 | $2\tau - 2\alpha \le t \le 2\tau + 2\alpha $ | $\frac{{4\alpha {\omega _Q}}}{T}(6{I_{y, 1}}{I_{y, 1}} + 6{I_{x, 1}}{I_{x, 1}} - I \cdot I)$ |
| δ10 | $2\tau + 2\alpha \le t \le 2\tau + 4\alpha $ | $\frac{{2\alpha {\omega _Q}}}{T}[6{I_{x, 1}}{I_{x, 1}} + 6{I_{y, 1}}{I_{y, 1}} - \frac{{12}}{\pi }({I_{x, 1}}{I_{y, 1}} + {I_{y, 1}}{I_{x, 1}}) - I \cdot I]$ |
| δ11 | $2\tau + 4\alpha \le t \le 2\tau + 7\alpha $ | $\frac{{3\alpha {\omega _Q}}}{T}[(6 - \frac{4}{\pi }){I_{x, 1}}{I_{x, 1}} + (6 + \frac{4}{\pi }){I_{y, 1}}{I_{y, 1}} - \frac{4}{\pi }({I_{x, 1}}{I_{y, 1}} + {I_{y, 1}}{I_{x, 1}}) - I \cdot I]$ |
| δ12 | $2\tau + 7\alpha \le t \le 2\tau + 8\alpha $ | $\frac{{\alpha {\omega _Q}}}{T}[(6 - \frac{{12}}{\pi }){I_{x, 1}}{I_{x, 1}} + (6 + \frac{{12}}{\pi }){I_{y, 1}}{I_{y, 1}} + \frac{{12}}{\pi }({I_{x, 1}}{I_{y, 1}} + {I_{y, 1}}{I_{x, 1}}) - I \cdot I]$ |
| δ13 | $2\tau + 8\alpha \le t \le 3\tau $ | $\frac{{{\omega _Q}}}{T}(12{I_{y, 1}}{I_{y, 1}} - I \cdot I)(\tau - 8\alpha )$ |
| δ14 | $3\tau \le t \le 3\tau + \tau '$ | $\frac{{{\omega _Q}}}{T}(12{I_{y, 1}}{I_{y, 1}} - I \cdot I)\tau '$ |
Referring to Table 3, it is noteworthy to consider the zeroth order term of the Magnus expansion for any of the sequences and evaluate this term in the limiting case when the pulse duration a = 0. In this case, any term given in Table 3 is zero and from Eq. (5) we find that the density matrix at t = 3τ is simply Iy, 1 (for the [x, y] cycle) corresponding to full refocusing of the ensemble.
| j1 | j2 | |
| x | y | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 - BI_{y, 1}^2 + CI_{x, 1}^2]$ |
| x | -y | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 - BI_{y, 1}^2 + CI_{x, 1}^2]$ |
| -x | y | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 - BI_{y, 1}^2 + CI_{x, 1}^2]$ |
| -x | -y | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 - BI_{y, 1}^2 + CI_{x, 1}^2]$ |
| y | x | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 + CI_{y, 1}^2 - BI_{x, 1}^2]$ |
| y | -x | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 + CI_{y, 1}^2 - BI_{x, 1}^2]$ |
| -y | x | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 + CI_{y, 1}^2 - BI_{x, 1}^2]$ |
| -y | -x | $ - \frac{{4{\omega _Q}}}{{\pi T}}[AI_{z, 1}^2 + CI_{y, 1}^2 - BI_{x, 1}^2]$ |
Using the results from Table 3 and Eq. (5) we have evaluated the density matrices for each of the eight cycles for COM-II. Table 4 highlights the results from this computation and shows that the general form is given by $\rho \propto - D{I_{y, 1}} - E{I_{y, 2}}$ (D and E are defined in Table 4). Taking the limit again for a = 0 corresponding to δ-function RF pulses yields $\rho \propto {I_{y, 1}}$ corresponding to complete refocusing of the magnetization. We note that the terms Iy, 2 from any of the [±x, ±y] cycles (Ix, 2 for the [±y, ±x] cycles) in Table 4 do not commute with the quadrupolar Hamiltonian and evolves to a detectable signal which results in a spectral distortion. The spectral distortion arises from the fact that the factor E in front of the term Iy, 2 for all [±x, ±y] cycles (Ix, 2 for all [±y, ±x] cycles) is a sine modulation in whereas the term δmultiplying Iy, 1 for all [±x, ±y] cycles (Ix, 2 for all [±y, ±x] cycles) is a cosine modulation in . The frequency dependence of the term E is asymmetric with , and as a consequence, the superposition of Dand E results in a spectrum that will be asymmetric in frequency and appear distorted.
| φ1 | φ2 | $\rho (3\tau )$ |
| x | y | $ - D{I_{y, 1}} - E{I_{y, 2}}$ |
| x | -y | $ - D{I_{y, 1}} - E{I_{y, 2}}$ |
| -x | y | $D{I_{y, 1}} + E{I_{y, 2}}$ |
| -x | -y | $D{I_{y, 1}} + E{I_{y, 2}}$ |
| y | x | $D{I_{x, 1}} - E{I_{x, 2}}$ |
| y | -x | $D{I_{x, 1}} - E{I_{x, 2}}$ |
| -y | x | $ - D{I_{x, 1}} + E{I_{x, 2}}$ |
| -y | -x | $ - D{I_{x, 1}} + E{I_{x, 2}}$ |
Referring to Table 4 we find that the addition of the cycles [x, y] and [x, -y], does not cancel the spectral distortion. In addition, the first 4-steps of the phase cycle given in Table 2 will not cancel the undesired terms Iy, 2 either. Our previous experimental and simulation results verified this result[12]. However, the addition of 2-steps for phase cycling, such as [x, y] and [-y, x] will suppress terms denoted E in the density matrix yielding only the terms δ which only has a cosine modulation with respect to ${\omega _Q}$. Moreover, one possible 4-step phase cycling scheme for suppressing the spectral distortion would be the combination of [x, y] + [x, -y] + [-y, x] + [-y, -x] cycles (note that the receiver would have to be cycled as [-y, -y, -x, -x] in this case). A second combination for a 4-step phase cycle would be the superposition of [-x, y] + [-x, -y] + [y, x] + [y, -x] cycles with the receiver set to [y, y, x, x]. The full eight step phase cycling combines both of these 4-step cycles and suppresses the sine terms E multiplying Ix, 2 and Iy, 2 in the densityma trices. However, the 2-step or 4-step phase cycles would not be expected to perform as robust as the full 8-step cycle as cancellation of receiver imbalance in the channels or phase transients may not be fully suppressed. For this reason, it is preferable to implement the full 8-step cycling for cancellation of finite pulse width effects and instrumental artefacts especially when high RF power is being applied. 2 Simulations
To further investigate the validity of our theoretical calculations, simulations were performed by the use of SIMPSON[16]software. Only one 2H nucleus with quadrupolar coupling up to second order was considered in the simulations. The static magnetic field was set to 9.4 T, and the quadrupolar coupling constant ηQ was set to 160 kHz with the asymmetry parameter set to 0. The powder averaging was performed using 256 (aCR, bCR) pairs ×1gCR angles, which was selected according to the REPULSON algorithm[17].
We show in Fig. 2 the simulated FID signals recorded right after the second 90° COM-II pulse by using RF field of 40 kHz. The 8-step phase cycling scheme was used. It is clear that the COM-II pulse generates normal echo signal. We point out that evaluating the time for each peak (τ2′) is straightforward with the consideration of the time-span of δ14 and we obtain τ′ = (6-2/p)a-5.36a. We have found that the calculated τ2′ value through our analytical expressions agrees well with our simulations in Fig. 2.

|
| Fig. 2 Simulated time domain signal recorded right after the second 90° COM-II pulse using RF field of 40 kHz. 8-step phase cycling was used to accumulate the signals |
We show in Fig. 3 the dependence of echo peak amplitude on the RF field used for single pulses and COM-II pulses. It appears that the amplitude of echo peak is always greater using COM-II pulses regardless of the RF field. This must be due to the fact that composite pulse allows achieving broadband excitation, and it indicates that the composite pulse could be preferable in 2H quadrupolar echo spectroscopy.
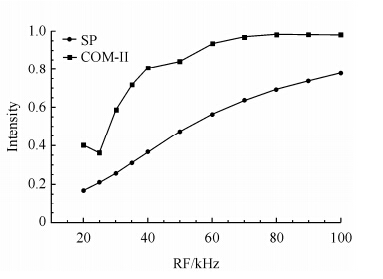
|
| Fig. 3 The dependence of the echo peak amplitude on the RF field applied for single 90° pulse (SP) or COM-II pulses (b). The echo peak amplitudes were extracted from corresponding time domain signals and were normalized with respect to that simulated using ideal pulses |
Lastly, we point out a subtle point regarding the application of composite pulses, as discussed in detail in references[6, 18] when fast exchange may take place on the time scale of the echo experiment. Composite pulse excitation may lead to additional line-shape distortions in situations of exchange—such artefacts cannot be suppressed by phase cycling. For such spin systems, it behoves the experimenter to investigate the acquired quadrupolar echo spectra as a function of echo spacing and/or pulse duration if composite pulses are applied whose duration is comparable to exchange times. 3 Conclusions
In this report, we have provided analytical results based on the leading order term in the average Hamiltonian theory for COM-II $(90\, \overline {180} \, 90\overline {\, 135\, } 45)$, which we found to be the most robust sequence investigated in our recent work on 2H quadrupolar echo spectroscopy[12]. We also show that a full 8-step phase cycle is robust in cancelling undesired terms in the density matrix that contribute to spectral distortions and should be applicable for quadrupolar echo spectroscopy based on composite pulses. Our simulations and computations fully confirm the previous experimental results. Detailed theoretical analysis could be further explored with the newly developed approach termed the Floquet-Magnus expansion[19].
Acknowledgement: The authors are grateful to the Key Project of Shanghai Committee of Science and Technology (11JC1403600), National Natural Science Foundation of China (21103050 and 21373086) and National Key Basic Research Program of China (2013CB921800). MS is grateful for financial support from the China Scholarship Council. Research performed at Brooklyn College of the City University of New York was supported by Award No. SC1 GM086268-08 from the National Institute of General Medical Science of the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.
| [1] | Jiang X, Rodriguez-Molina B, Nazarian N, et al. Rotation of a bulky triptycene in the solid state:toward engineered nanoscale artificial molecular machines[J]. J Am Chem Soc, 2014, 136:8 871-8 874. |
| [2] | Walaszek B, Adamczyk A, Pery T, et al. 2H solid-state NMR of ruthenium complexes[J]. J Am Chem Soc, 2008, 130:17 502-17 508. |
| [3] | Tardy-Laporte C, Arnold A A, Genard B, et al. A 2H solid-state NMR study of the effect of antimicrobial agents on intact Escherichia coli without mutating[J]. Biochim Biophys Acta, 2013, 1828:614-622. |
| [4] | Heaton N J, Vold R R, Vold R L. Deuterium quadrupole-echo NMR spectroscopy. IV. Inversion of full width deuterium powder patterns[J]. J Magn Reson, 1988, 77(1 969):572-576. |
| [5] | Greenfield M S, Ronemus A D, Vold R L, et al. Deuterium quadrupole-echo NMR spectroscopy. III. Practical aspects of lineshape calculations for multiaxis rotational processes[J]. J Magn Reson, 1987, 72(1 969):89-107. |
| [6] | Barbara T M, Greenfield M S, Vold R L, et al. Deuterium quadrupole echo NMR spectroscopy. I. Effects of chemical exchange during single and composite pulses[J]. J Magn Reson, 1986, 69(1 969):311-330. |
| [7] | Ronemus A D, Vold R L, Vold R R. Deuterium quadrupole echo NMR spectroscopy II. Artifact suppression[J]. J Magn Reson, 1986, 70(1 969):416-426. |
| [8] | Iijima T, Shimizu T, Nishimura K. 2H NMR pure-quadrupole spectra for paramagnetic solids[J]. J Magn Reson, 2015, 251:57-64. |
| [9] | Sun C, Boutis G S. Simulation studies of instrumental artifacts on spin I=1 double quantum filtered NMR spectroscopy[J]. J Magn Reson, 2010, 205:102-108. |
| [10] | Rosal I d, Gutmann T, Maron L, et al. DFT 2H quadrupolar coupling constants of ruthenium complexes:a good probe of the coordination of hydrides in conjuction with experiments[J]. Phys Chem Chem Phys, 2009, 11:5 657-5 663. |
| [11] | Michal C A, Wehman J C, Jelinski L W. Deuterium quadrupole-coupling and chemical-shielding tensors in the model dipeptide glycylglycine monohydrochloride monohydrate[J]. J Magn Reson (Series B), 1996, 111:31-39. |
| [12] | Shen M, Roopchand R, Mananga E N S, et al. Revisiting NMR composite pulses for broadband 2H excitation[J]. Solid State Nucl Magn Reson, 2015, 66-67:45-48. |
| [13] | Mananga E S, Rumala Y S, Boutis G S. Finite pulse width artifact suppression in spin-1 quadrupolar echo spectra by phase cycling[J]. J Magn Reson, 2006, 181:296-303. |
| [14] | Haeberlen U, Waugh J S. Coherent averaging effects in magnetic resonance[J]. Phys Rev, 1968, 175:453-467. |
| [15] | Vega S, Pines A. Operator formalism for double quantum NMR[J]. J Chem Phys, 1977, 66:5 624. |
| [16] | Bak M, Rasmussen J T, Nielsen N C. SIMPSON:A general simulation program for solid-state NMR spectroscopy[J]. J Magn Reson, 2000, 147:296-330. |
| [17] | Alderman D W, Solum M S, Grant D M. Methods for analyzing spectroscopic line shapes. NMR solid powder patterns[J]. J Chem Phys, 1986, 84:3 717. |
| [18] | Siminovitch D J, Raleigh D P, Olejniczak E T, et al. Composite pulse excitation in quadrupole echo spectroscopy[J]. J Chem Phys, 1986, 84:2 556. |
| [19] | Bain A D, Dumont R S. Introduction to Floquet theory:The calculation of spinning sideband intensities in magic-angle spinning NMR[J]. Concept Magn Reson, 2001, 13:159-170. |
 2015, Vol. 32
2015, Vol. 32