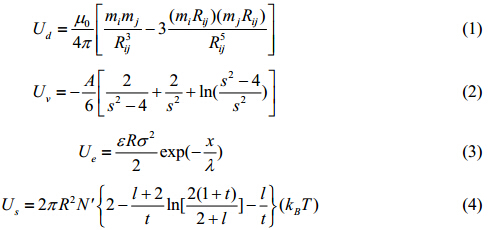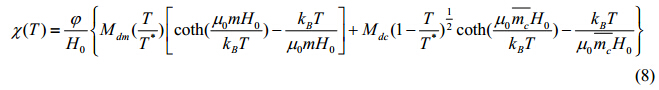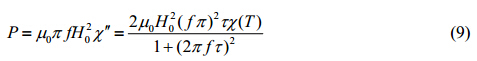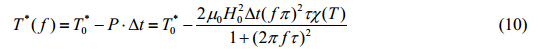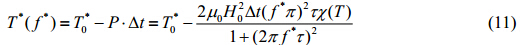文章信息
- 汪臣才,李昭,林永雅
- WANG Chen-cai, LI Zhao, LIN Yung-ya
- 优化磁共振纳米医学中磁性纳米粒子的热疗效率
- Optimizing Magnetic Nanoparticle Hyperthermia Effect in Magnetic Resonance Nanomedicine
- 波谱学杂志, 2015, 32(2): 248-260
- Chinese Journal of Magnetic Resonance, 2015, 32(2): 248-260
- http://dx.doi.org/10.11938/cjmr20150208
-
文章历史
- 收稿日期:2015-03-22
- 收修改稿日期:2015-05-15
Introduction
Magnetic nanoparticles have found popular applications in magnetic resonance molecular imaging and nanomedicine for medical diagnosis and therapy. Because these nanoparticles are biocompatible, injectable, nontoxic, and are able to target specific tissues through specific (e.g., antibody-antigen) and non-specific (e.g., enhanced permeability and retention effect) targeting mechanisms, they can serve as “molecular beacons” to enhance the MR image contrast for early tumor detection. Moreover, through interacting with external alternating magnetic fields, these magnetic nanoparticles accumulated at the tumor site can generate heat through Neel relaxation and/or Brownian relaxation[1, 2, 3, 4]. Through magnetic resonance hyperthermia, magnetic nanoparticles can serve as “molecular bullets” to kill cancer cells, leaving surrounding healthy tissues unaffected. Such hyperthermic effects can also be used for thermal activation and control releasing of cancer drugs.
However, pre-clinical and clinical applications of magnetic resonance hyperthermia with magnetic nanoparticles is limited by a few major theoretical difficulties and experimental challenges. For example, conventional theoretical models for magnetic resonance hyperthermia assume that the magnetic nanoparticles act independently as single units and are dispersed uniformly in the colloidal suspension, thus making the interaction among the nanoparticles negligible. However, in real biomedical applications, when magnetic nanoparticles have been injected into blood vessels or been bound to cancer cells through the antibody-antigen interaction, individual nanoparticles are highly likely to aggregate and form clusters. The resulting aggregation state changes the physical properties of the magnetic nanoparticle suspension, such as magnetic susceptibility. Furthermore, aggregate formation and disruption were found to be affected by external magnetic field conditions[5]. Consequently, a higher magnetic field strength is required to disrupt these aggregates, lowering the overall heating efficiency of the magnetic nanoparticle suspension. To optimize the heating efficiency for magnetic resonance hyperthermia, further understanding and formulation of aggregate formation and disruption is needed.
Previous magnetic resonance experiments have demonstrated that the thermal disruption of magnetic nanoparticle dimers is a second-order phase transition[6], where the critical temperature for this second-order phase transition was then further characterized[7]. The inverse susceptibility-temperature curve of magnetic nanoparticle aggregates was also shown to respond differently to the frequency of the external magnetic field[8]. Because the critical temperature is a function of the external alternating magnetic field frequency and the heat-generation mechanism is closely related to the relaxation effects under such magnetic field, the frequency at which the aggregates of magnetic nanoparticles completely disrupt into monomers can be described by the critical temperature. In this paper, we aim to illustrate the relationship between the critical temperature and its corresponding critical frequency by a revised Langevin function. 3D cluster-moving based Metropolis Monte Carlo method is used to simulate the thermodynamic behavior and the aggregation/ disruption of the magnetic nanoparticles under different temperatures. This critical frequency can then serve as an important reference for optimizing the heating efficiency of the magnetic nanoparticles. We hypothesize that preheating the magnetic nanoparticles at the critical frequency to disrupt all clusters present in the colloidal suspension can minimize the loss of energy and therefore optimize the heating efficiency for magnetic resonance hyperthermia. 1 Theory 1.1 Formation of aggregates among magnetic nanoparticles
At room temperature, magnetic nanoparticles are stabilized in the colloidal suspension by various interactions[9] between nanoparticles, including inter-particle repulsions (e.g., electrostatic repulsion and steric repulsion) and inter-particle attractions (e.g., magnetic dipole-dipole interaction and van der Waals force). For example, for any two magnetic nanoparticles i and j with center-to-center distance r, if we assume the surface distance between these two particles is x, radii Ri and Rj, magnetic moments mi and mj, thickness of surface coating δ, and the distance vector pointed from nanoparticle i to j is Rij, then the interaction energies among magnetic nanoparticles can be described as:
and the total interaction energy as:
where m0is the permeability of free space, A the Hamaker constant for van der Waals interaction (associated with the magnetic nanoparticle surface coating layer and the dielectric properties of carrier liquid), ethe dielectric constant of the solvent, sthe surface potential of the particle, λthe Debye length, kB the Boltzmann constant, T the absolute temperature of colloidal magnetic nanoparticle suspension, and N′ the number of molecules adsorbed on the surface of nanoparticles.$s = \frac{x}{R} + 1$, $l = \frac{{{R_{ij}} - 2R}}{R}$ , $t = \frac{\delta }{R}$.Ud, Uv, Ue, and Us denote the magnetic dipole-dipole interaction, van der Waals’ interaction, electrostatic repulsion, and steric repulsion, respectively. For the diluted nanoparticle concentrations used in MR nanomedical, theranostic applications, only the dominating dipole-dipole interaction term is considered. With higher nanoparticle concentrations and thus closer nanoparticle spacing, multipolar interactions need to be included as well[2]. Consequently, the interactions between magnetic nanoparticles depend on a number of factors such as temperature, magnetic field strength, particle size, and particle concentration (since the concentration determines the distance between the nanoparticles). The kinetic energy of the nanoparticles is not sensitive to the parameters such as temperature, magnetic field strength, particle size, and particle concentration, and therefore can be conveniently neglected (i.e., treated as a constant).
The colloidal magnetic nanoparticle suspension must sustain a balance between attraction and repulsion to maintain the stability, as any change in the external environment, such as temperature, concentration, or applied magnetic field, can influence the interaction among nanoparticles. For example, when the mutual repulsion among particles is smaller than the mutual attraction, magnetic nanoparticles tend to aggregate; in contrast, when the repulsion is larger than the attraction, magnetic nanoparticle aggregates will be disrupted into individual particles. For a certain colloidal magnetic nanoparticle suspension, adjusting experimental parameters and therefore controlling the aggregation/disruption of magnetic nanoparticles is essential for optimizing the heating efficiency of magnetic resonance hyperthermia. 1.2 Critical frequency and critical temperature under an alternating magnetic field
The relative amounts of monomers and clusters in the colloidal magnetic nanoparticle suspension can be expressed as Pm and Pc [10], respectively:
where T is the absolute temperature of suspension and T* the critical temperature for second-order phase transition. Based on the Langevin function, the equilibrium magnetic susceptibility for the mixed system can thus be described as[10]
where kB represents the Boltzmann constant, j the volume fraction of magnetic nanoparticles, H0 the strength of external alternating magnetic field, m0 the permeability of free space, Mdm and Mdc the saturation magnetization for monomers and clusters, respectively, and m and the average magnetic moment for monomers and clusters, respectively. When excited by an external magnetic field, magnetic nanoparticles generate heat through relaxation mechanisms, such as Brownian relaxation and Neel relaxation[11, 12, 13, 14]. The power dissipation can be expressed as[12]
A portion of the dissipated energy contributes to the raise in temperature of magnetic nanoparticles, where another portion to the acceleration of aggregate disruption. This distribution results in a lower critical temperature for the second order phase transition. If the unmodified critical temperature is given by $T_0^*$, the frequency of the magnetic field as f*, and the heating duration as Dt, the critical temperature can be revised to a function of frequency[8]
If the heating duration is fixed, then the relationship between the critical frequency f* and critical temperatureT*(f*) can be represented as
2 Methods3D cluster-moving based Metropolis Monte Carlo method was used to simulate the thermodynamic behavior and to study the aggregation/disruption of magnetic nanoparticles at various temperatures. The Metropolis Monte Carlo method provides a universally applicable model and faster convergence. For this simulation, the magnetic nanoparticles were assumed to be distributed in a 3D cube, and their size as a log-normal distribution to ensure the model similar to the experimental scenario[15]. 2.1 Setup of model and parameters
The magnetic nanoparticles were set to have sizes following a log-normal distribution $(\overline D , {\rm{ }}\sigma {\rm{)}}$ and distributed randomly in a cube with edge λ. The diffusion is modeled by a random walk. The thickness of surface coating of each nanoparticle is set as δ, the total number of magnetic nanoparticles as N, the volume fraction of magnetic nanoparticles as φ, and the saturation magnetization as M. The magnetic moment can thus be represented as $m = \frac{{\pi M{D^3}}}{6}$, pointing to an arbitrary angle that ranges from 0 to 2π. For any magnetic nanoparticle i, its current state can be determined by four variables (xi, yi, zi, θi), where (xi, yi, zi) denotes the spatial coordinates and θi the angle between the magnetic moment mi and external magnetic field H. The distance vector points from nanoparticle i to j was set as Rij, and the unit vector rij was set in the same direction as Rij, where ni and nj are unit vectors along the direction of magnetic moment mi and mi, respectively. The total energy Ui of any magnetic nanoparticle i under the external magnetic field can then be written as
where Udi signifies the magnetic dipole-dipole interaction, Uvi the van der Waals’ interaction, Uei the electrostatic repulsion, Usi the steric repulsion, and Uhi the interaction between individual nanoparticle and the external magnetic field. However, in our simulation considering about the general case, electrostatic repulsion was neglected since neutralized free magnetic particles dispersed in suspension, so the common interactions among magnetic nanoparticles were magnetic dipole-dipole interaction, van der Waals’ interaction and steric repulsion.
The specific values of parameters used in the computer simulation include the average diameter of the magnetic nanoparticles $\overline D = 11.5{\rm{ nm}}$, standard deviation of the particle size distribution σ =0.20 nm, volume fraction φ = 0.01, total number of magnetic nanoparticles N = 300, edge of the cube $L = 167.25\overline D $, thickness of the surface coating $\delta = 0.15\overline D $, saturated magnetization M = 414 kA/m, magnetic field strength H = 400A/m, permeability of free space ${\mu _0} = 4\pi \times {10^{ - 7}}{\rm{H/m}}$, Boltzmann constant ${k_B} = 1.38 \times {10^{ - 23}}{\rm{J}}/{\rm{K}}$, Hamaker constant $A = {10^{ - 19}}{\rm{J}}$ (corresponding to common organic layers surface coating such as glycerol in water solution), and total number of molecules absorbed on the surface per surface area $N' = {10^{18}}/{{\rm{m}}^2}$. 2.2 Cluster-moving-based Metropolis Monte Carlo simulation
The interactions within the aggregating magnetic nanoparticle clusters are stronger than the interactions between clusters and the surrounding monomers in an actual colloidal magnetic nanoparticle suspension. The nanoparticle dynamics can be described by deterministic equations (e.g., Newton’s second law) or stochastic equations (e.g., Fokker-Planck equation). In our molecular dynamics simulations, without loss of generality and accuracy, the nanoparticle dynamics is approximated by 3D random walk with fixed step length and variable walking direction (uniform sampling in the spherical coordinates) that satisfy the experimental translational and rotational diffusion coefficients. The choices of step length, 0.5δ, and maximum rotation angle per step, p/18, is to speed up the expensive calculation without compromising the accuracy.
To better simulate the effect resulting from changes in position and energy, a cluster-moving algorithm was employed to describe particles’ random walk. The procedures for the cluster-moving-based Metropolis Monte Carlo simulation are described as follows:
(1) Initialize the system and all parameters.
(2) Change the state of the (i = 1, 2, 3, …, N) magnetic nanoparticle (xi, yi, zi, θi).
(3)Calculate the energy change for the system, ΔDU = Ucurrent - Uprevious, and verify whether the new state is acceptable by the Metropolis algorithm, as the system always prefers lower energy during evolution. If ΔDU< 0, then accept the new state of the ith magnetic nanoparticle. If ΔDU > 0, then calculate $h = \exp ( - \frac{{\Delta U}}{{{k_B}T}})$ and compare to temp, a random number ranges from 0 to 1. If h > temp, accept the new state. If h < temp, reject the new state and maintain the previous state of the ith magnetic nanoparticle.
(4) Repeat step (2) and (3) until the states of all N magnetic nanoparticles have been changed. Record current Monte Carlo steps Nm = 1.
(5) Calculate the surface distance among all magnetic nanoparticles in the suspension. If the distance is smaller than $0.25\overline D $, assume an aggregate is formed.
(6) Repeat steps (2) through (5) until Nm = 2 000 000to ensure the system has reached equilibrium.
To avoid complicated calculations for the center of mass of aggregates, the movement, orientation, and magnetic moment of an aggregate were represented by those of an arbitrary particle within that aggregates. The steps for each random walk were set as , and the rotation angle for the magnetic moment as $\Delta \theta = \frac{\pi }{{18}}$. 3 Results and discussions 3.1 Simulation results of the aggregates formation
By employing the 3D cluster-moving-based Metropolis Monte Carlo method, we studied the thermodynamic behavior of 300 magnetic nanoparticles with a temperature range from 300 K to 450 K (27 ℃ to 177 ℃). The formation and disruption of magnetic nanoparticle aggregates at different temperatures were analyzed by calculating the interactions between the magnetic nanoparticles. To highlight this point, we randomly chose one magnetic nanoparticle and calculated its interaction energies evolving with Monte Carlo steps at T = 300 K according to Eq. (12), as shown in Table 1. What’s more, by assuming that clusters would form when the surface distance between particles is smaller than $0.25\overline D $, we obtained the distribution of monomers and aggregates when the system is at equilibrium, as illustrated in Fig. 1. At room temperature T = 300 K and T = 310 K, aggregates with various size/structure were formed among magnetic nanoparticles. However, when the temperature was increased to T = 350 K and T = 360 K, aggregates first disrupted into smaller portions, then into monomers. When the temperature was further increased to T = 400 K and T = 450 K, the majority of the nanoparticles in the system was in the monomeric form. It suggests that the attractive and repulsive interactions become balanced at higher temperatures.
| Monte carlo steps | U | Ud | Uv | Us | Uh |
| 0 | 1.7770×10-21 | 3.8729×10-24 | -5.2130×10-27 | 1.8267×10-21 | -5.3522×10-23 |
| 10 | 3.1940×10-21 | 4.5583×10-24 | -2.3155×10-27 | 3.3207×10-21 | -1.3127×10-22 |
| 100 | 3.6034×10-21 | 9.5663×10-24 | -4.6260×10-27 | 3.7501×10-21 | -1.5693×10-22 |
| 1000 | 2.5901×10-21 | 2.6149×10-24 | -2.0991×10-27 | 2.6828×10-21 | -9.5298×10-23 |
| 10000 | 3.7607×10-21 | 1.0562×10-23 | -2.8352×10-27 | 3.9184×10-21 | -1.6821×10-22 |
| 50000 | 1.8502×10-21 | -6.3504×10-26 | -1.6851×10-26 | 1.9074×10-21 | -5.7140×10-23 |

|
| Fig. 1 Distribution of monomers and clusters in magnetic nanoparticle suspension at equilibrium at different temperatures. (a) T = 300 K, (b) T = 310 K, (c) T = 350 K, (d) T = 360 K, (e) T = 400 K, (f) T = 450 K. To aid the 3D visual effect, z-coordinates of the magnetic nanoparticles are color-coded |
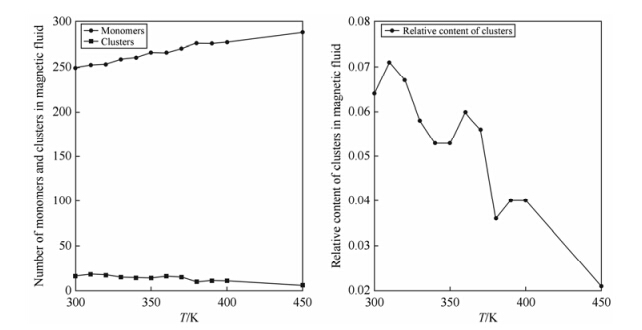
Based on the simulation results, the relative contents of aggregates and monomers in the magnetic nanoparticle suspension were assessed at different temperatures, as shown numerically in Table 2 and diagrammatically in Fig. 2. With the elevation of temperature, the relative content of monomers was found to increase, while that of aggregates to decrease. Fluctuations observed in Fig. 2 are mainly due to the disruption of larger aggregates into smaller portions, resulting in a relative increase in the number of aggregates.
| Temperature | Aggregates | Monomers | Relative content |
| 300 K | 16 | 249 | 0.064 |
| 310 K | 18 | 252 | 0.071 |
| 320 K | 17 | 253 | 0.067 |
| 330 K | 15 | 258 | 0.058 |
| 340 K | 14 | 260 | 0.053 |
| 350 K | 14 | 266 | 0.053 |
| 360 K | 16 | 266 | 0.060 |
| 370 K | 15 | 270 | 0.056 |
| 380 K | 10 | 276 | 0.036 |
| 390 K | 11 | 276 | 0.040 |
| 400 K | 11 | 277 | 0.040 |
| 450 K | 6 | 288 | 0.021 |
|
| Fig. 2 Relative content of clusters in suspension at different temperatures |
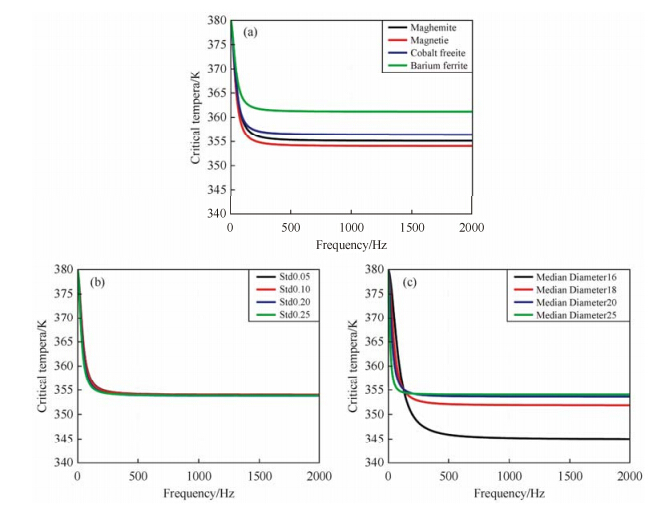
According to Eq. (10) and (11), the critical temperature can be reduced if an external alternating magnetic field with higher frequency is applied. To further explore the relationship between the critical temperature and magnetic field frequency, the critical temperature was plotted as a function of magnetic field frequency under various scenarios shown in Fig. 3. All results revealed similar trends where the critical temperature decreased dramatically as the frequency increased from 0 Hz, but remained unaffected once the frequency reached a certain critical value. Such critical value of the frequency is then defined as the “critical frequency” of the corresponding colloidal magnetic nanoparticle suspension. Heating at or above the critical frequency can optimize the heating efficiency, resulting in the complete disruption of aggregates into monomers.
|
| Fig. 3 The critical temperature for cluster disruption of magnetic nanoparticle suspension as a function of external magnetic field frequency. (a) The critical temperature for cluster disruption of different magnetic nanoparticle suspensions versus external magnetic field frequency. (b) The critical temperature for cluster disruption of magnetite versus external magnetic field frequency under different size distributions (same median diameter $\overline D = 20.00{\rm{ nm}}$, the standard deviations shown in the figure are all in the unit of nm).(c) The critical temperature for cluster disruption of magnetite versus external magnetic field frequency under different median diameters (same size distribution σ = 0.25 nm) |
Fig. 3 (a) shows curves of the critical temperature vs. magnetic field frequency for suspensions containing four commonly used magnetic materials (listed in Table 3). When the magnetic field frequency is lower than 300 Hz, the critical temperature dramatically decreases with the increase in frequency. Continual increase in frequency does not result in a further obvious decrease in critical temperature, while at frequency values higher than 500 Hz, the critical temperature no longer decreases, but rather becomes stable. This indicates a critical frequency of around 500 Hz for all of the four magnetic materials studied, despite of their different final critical temperatures, range from 354 K to 362 K.
| Magnetic solid | Chemical formula | Md/(kA·m-1) | K/(kJ·m-3) | c/(J·kg-1·K-1) | r/(kg·m-3) |
| Maghemite | g -Fe2O3 | 414 | 15 | 746 | 4600 |
| Magnetite | FeO·Fe2O3 | 446 | 23 | 670 | 5180 |
| Cobalt Ferrite | CoO·Fe2O3 | 425 | 180 | 700 | 4907 |
| Barium Ferrite | BaO·6Fe2O3 | 380 | 300 | 650 | 5280 |
In a real suspension, the sizes of magnetic nanoparticles usually obey the log-normal distribution with a certain standard deviation. Therefore we take magnetite, which is the most strongly magnetic mineral in nature, as an example and further discuss how the size distribution of magnetic nanoparticles affects the relationship between the critical temperature and the magnetic field frequency. When the mean diameter of the magnetic nanoparticles in the suspension is fixed, different size distributions does not cause notable changes in the critical temperature vs. magnetic field frequency curve, as shown in Fig. 3(b). When the size distribution is fixed, however, changing the mean diameter of the magnetic nanoparticles significantly changes the critical temperature vs. magnetic field frequency curve, as shown in Fig. 3(c). A decrease in mean diameter from 25 nm to 16 nm displays a much higher critical frequency requirement to disrupt the aggregates. 4 Conclusion
Magnetic nanoparticles have found popular applications as “molecular beacons” for medical diagnosis and as “molecular bullets” for targeted therapy. Consequently, the sensitive detection[16, 17, 18] and effective heating of magnetic nanoparticles are fundamental to the development of magnetic resonance molecular imaging and nanomedicine. For nanomedical, theranostic applications of magnetic resonance hyperthermia in cellular environments, the interactions between the nanoparticles with the other nanoparticles and with surrounding biomolecules such as proteins, lipids and sugars (all of which could be electrically charged) and small ions (cations and anions) could be significant and generally discount the heating efficiency[19]. As a first step in optimizing the hyperthermia effect, the thermodynamic behavior of magnetic nanoparticles and aggregation dynamics were studied in this work. 3D cluster-moving-based Monte Carlo method was used to simulate the thermodynamic behavior of the magnetic nanoparticles and to further analyze the monomer/aggregate distribution at various temperatures. Simulation results show that the relative content of aggregates decreases with the increase in temperature, until all the particles exist as monomers at or above the critical temperature. The critical temperature is further found to be related to the frequency of the external alternating magnetic field, where the critical temperature continually decreases with the increase in frequency until the critical frequency is reached. Any increase in frequency beyond this point no longer affects the critical temperature. Our simulation suggests that the heating efficiency of magnetic nanoparticle suspension may be optimized for its potential applications in magnetic resonance hyperthermia by preheating the colloidal suspension at the critical frequency to disrupt aggregates into monomers.
| [1] | Jordan A, Wust P, Fähling H, et al. Inductive heating of ferrimagnetic particles and magnetic fluids:physical evaluation of their potential for hyperthermia[J]. Int J Hyperther, 2009, 25:499-511. |
| [2] | Krishnan K M. Biomedical Nanomagnetics:A spin through possibilities in imaging, diagnostics, and therapy[J]. IEEE Trans Magn, 2010, 46:2 523-2 558. |
| [3] | Gordon R T, Hines J R, Gordon D A. Biophysical approach to cancer treatment via intracellular temperature and biophysical alterations[J]. Med Hypotheses, 1979, 5:83-102. |
| [4] | Jordan A, Wust P, Scholz R, et al. Cellular uptake of magnetic fluid particles and their effects on human adenocarcinoma cells exposed to AC magnetic fields in vitro[J]. Int J Hyperther, 1996, 12:705-722. |
| [5] | Alexey O I, Sofia S K, Valentin S M, et al. Ferrofluid aggregation in chains under the influence of a magnetic field[J]. J Magn Magn Mater, 2006, 300(l):e206-e209. |
| [6] | Morais P C, Gonçalves G R R, Bakuzis A F, et al. Experimental evidence of dimer disruption in ionic ferrofluid:A ferromagnetic resonance investigation[J]. J Magn Magn Mater, 2001, 225:84-88. |
| [7] | Zhong J, Xiang Q, Massa L O, et al. Second-order-like cluster-monomer transition within magnetic fluids and its impact upon the magnetic susceptibility[J]. Nanoscale Res Lett, 2012, 7:167. |
| [8] | Du Z, Liu W, Zhong J, et al. Signature of cluster disruption within magnetic fluid samples:The key information provided by low frequency alternating current susceptibility measurements[J]. J Appl Phys, 2014, 115:194310. |
| [9] | Ganguly R, Zellmer B, Puri I K. Field-induced Self-assembled ferrofluid aggregation in pulsatile flow[J]. Phys Fluids, 2005, 17:097104. |
| [10] | Xiang Q, Zhong J, Zhou M, et al. AC field dependence of cluster disruption in magnetic fluids[J]. J Appl Phys, 2011, 109:07B317. |
| [11] | Wang X, Gu H, Yang Z. The heating effect of magnetic fluids in an alternating magnetic field[J]. J Magn Magn Mater, 2005, 293:334. |
| [12] | Rosensweig R E. Heating magnetic fluid with alternating magnetic field[J]. J Magn Magn Mater, 2002, 252:370. |
| [13] | Ondeck C L, Habib A H, Ohodnicki P, et al. Theory of magnetic fluid heating with an alternating magnetic field with temperature dependent materials properties for self-regulated heating[J]. J Appl Phys, 2009, 105:07B324. |
| [14] | Skumiel A, Łabowski M. The heating effect of the biocompatible ferrofluid in an alternating magnetic field[J]. Molecular and Quantum Acoustics, 2006, 27:233-238. |
| [15] | Chantrell R W, Popplewell J, Charles S W. Measurements of particle-size distribution parameters in ferrofluids[J]. IEEE Trans Magn, 1978, 14 (5):975-977. |
| [16] | Hwang D W, Lin Y Y, Hwang L P. Studies of magnetic resonance imaging with active feedback RF field[J]. Chinese J Magn Reson, 2010, 27 (3):409-416. |
| [17] | Huang S Y, Walls J D, Lin Y Y. Periodic control of spin turbulence in solution magnetic resonance[J]. Chinese J Magn Reson, 2010, 27 (3):425-435. |
| [18] | Li Z, Hsu C H, Dimitrov N, et al. Sensitive imaging of magnetic nanoparticles for cancer detection by active feedback MR[J]. Magn Reson Med, 2015, DOI:10.1002/mrm.25632. |
| [19] | Hilger I, Kaiser W A. Iron oxide-based nanostructures for MRI and magnetic hyperthermia[J]. Nanomedicine 2012, 7(9):1 443-1 459. |
 2015, Vol. 32
2015, Vol. 32