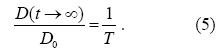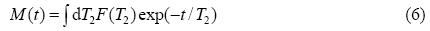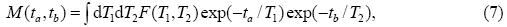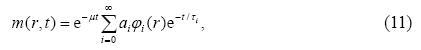文章信息
- 宋一桥
- SONG Yi-qiao
- 低场核磁共振:弛豫和扩散的多维实验
- Low Field Magnetic Resonance:Multi-Dimensional Experiments of Relaxation and Diffusion
- 波谱学杂志, 2015, 32(2): 141-149
- Chinese Journal of Magnetic Resonance, 2015, 32(2): 141-149
- http://dx.doi.org/10.11938/cjmr20150201
-
文章历史
- 收稿日期:2015-02-12
- 收修改稿日期:2015-05-14
Porous materials (PM), from construction materials to biological tissues,fill our environment and perform essential functions in our modern lives. Both water and petroleum come from subsurface reservoirs within the porous rocks of Earth's sedimentary crust. The scale of our energy need is one of the most prominent drivers for scientific and technological development as well as global politics and economy.
Porous media are generally considered as material with structures of importance at length scales larger than atoms and these structures are essential for the material properties and performance[1]. For example,fluid transport is an essential property for many porous media from water and contamination movement in aquifers,chemical reactions in porous catalysts,filtration,gas exchange in lung tissue,and blood and oxygen perfusion in brain and cancer growth. Magnetic resonance (MR) is uniquely suited for such studies primarily because the pore filling fluid can be measured through spin relaxation,diffusion,flow and imaging experiments. Furthermore,MR experiment can be performed without physical contact of the sample,an advantage that cannot be overemphasized. Low-field MR exhibits further advantage due to its smaller size,lower cost for broader applications. This article will summarize a few aspects of Low-field MR research with a focus of the essential physical processes and the methodology development in the past two decades.
1 Physics: surface relaxation and restricted diffusion 1.1 Spin relaxation and diffusionSpin relaxation is a key parameter describing the dynamics of the spins and its interaction with the surrounding environment. Both relaxation and translational diffusion are sensitive to molecular sizes and thus can be used to obtain molecular composition information from pure liquids,mixtures and fluid phases[2].
Diffusion of solid spherical particles can be well described by the Stoke-Einstein relationship. However,for molecules of long chain,e. g. polymers,hydrocarbon chains,the internal molecular motion can have a significant effect on the diffusion and rotational properties. For such chain molecules,a power law scaling theory is more applicable[3, 4] to describe the relationship between molecular size and relaxation/diffusion behavior,
where Ni is the chain length of the i-th component, $\bar N$ is the average chain length. This scaling relationship can be used to obtain mixture composition directly from diffusion and relaxation,for example,using low field NMR[3, 4].
1.2 Relaxation in porous mediaWhen a fluid saturates the pore space,interaction between the fluid molecules and the solid surface may contribute to additional relaxation,a phenomenon called surface relaxation. Independent of the mechanism of surface relaxation,the experimentally measured relaxation rate is found to be proportional to SVR. This may be understood by considering only a surface layer of the fluid is affected by the surface relaxation with the strength to be parametrized as the surface relaxivity,r (Fig. 1),
 |
| Fig.1 Surface relaxation behavior in porous media |
where T2b is the bulk relaxation,S is the surface area and Vp is the pore volume. The validity of the above equation[5, 6] assumes that the water molecules diffuse rapidly between the surface and the bulk regions within the T2 time scale,so-called fast diffusion limit. Brownstein and Tarr[7] described an analytical solution of diffusion-relaxation equations in a few simple geometries demonstrating the importance of diffusion in relaxation interpretation. This theory can be extended to arbitrary pore geometries and also to solve the combined relaxation and diffusion problem with regard to multi-dimensional NMR experiments[8, 9].
1.3 Restricted diffusion in complex mediaIt is well-known that a porous structure reduces the diffusion of molecules in the pore-filling fluid with its bulk diffusion coefficient D0,e.g. Fig. 2. Solid porous materials such as rock and soil are,to an approximation,a packing of solid particles with interstitial space occupied by fluids. In biological tissues,cell membranes exhibit finite permeability to water transport thus limiting diffusion in tissues.
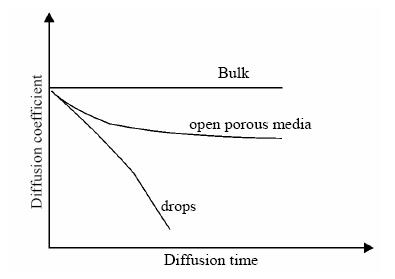 |
| Fig. 2 Behavior of diffusion coefficient as a function of diffusion time for bulk liquid, open porous media, and closed system |
For a fluid drop,the long time displacement is finite and limited by the size of the enclosing structure,thus the mean square displacement is
where P is the diffusion propagator and P = 1/Vp at long time. For a sphere of diameter d, $ < \Delta {r^2} > = 3{d^2}/10\,.$ This phenomenon has been used to characterize emulsions[10, 11].
For an open porous system where the pore space is interconnected,there are two aspects of this effect. One is that at short diffusion time,those molecules near the surface of the solid matrix (or grains) have less free space to diffuse and the net displacement is reduced. This effect is directly proportional to SVR of the material and it is often characterized by a reduced diffusion coefficient[12],
where D0 is the bulk diffusion coefficient,and D(t) is the diffusion coefficient at the diffusion time t. A is a constant dependent on dimensionality. The approximation is valid when the diffusion distance $\sqrt {{D_0}t} $ is much less than pore size. Here the diffusion coefficient is defined as $ < \Delta x{(t)^2} > /2t,$ where x(t) is the net displacement along one direction at time t and $ < \Delta x{(t)^2} > $ is the mean square displacement. For isotropic diffusion in three dimensions,D(t) can also be defined from the vector displacement $\Delta r:D(t) = < \Delta r{(t)^2} > /6t.$
The second effect is the long diffusion time when $\sqrt {{D_0}t} $ is larger than the pore size. For such open systems,D(t) will approach a constant at long time,but $D(t \to \infty ) < {D_0}$. This is because the diffusing molecules have to travel around the grains so that the distance to travel in order to achieve a displacement x is larger than x. In other words,such molecules have to meander around the grains (geometrical obstacles). This reduction of diffusion defines the tortuosity factor T [13],
For more theoretical review of the physics of diffusion in porous media,please refer to Refs. [14, 15, 16].
2 Multidimensional NMR of relaxation and diffusionConventional NMR relaxation and diffusion techniques measure one parameter (e.g. T1 and T2,T1r,or D) in a single experiment. For a single species of spins,the signal decays in an exponential functional form. For mixtures,the total signal (M) will be a superposition of all components. With a change of variable,the signal can be obtained by integrating along T2:
where F(T2) is the T2 distribution or called spectrum. However,in a more complex sample,such as a porous rock saturated with a mixture of water and oil,the relaxation time constant of water and oil may be similar due to a combination of oil molecular size and water surface relaxation.
The newly developed multi-dimensional (MD) NMR technique improves the resolution of different molecules by measuring the correlation function of two or more parameters,such as T1-T2 correlation,D-T2,T1-T2-D,D-D,etc. The fluid can be described by two parameters,such asT1 and T2,and the signal is
where f(T1,T2) is the two-dimensional distribution function,or 2D spectrum of the sample. This T1-T2 correlation experiment uses two experimental parameters: ta for the T1 recovery time,and tb for the T2 decay time. Typically,for every value of ta,data at the full range of tb is acquired. MD NMR is typically performed by varying two or more experimental parameters and acquires NMR signals accordingly as a matrix. Laplace inversion of such MD matrices is used to obtain the multi-parameter correlation functions.
This type of correlation experiments was first reported in 1990s[17, 18],however,data analysis was then difficult due to limited computing power. In early 2000,a new algorithm was developed to perform the MD Laplace inversion on regular PCs and laptops[19] spurring a rapid expansion of applications of the MD methodology in many fields[19, 20, 21, 22, 23, 24, 25]. In particular,it has been since applied commercially in petroleum exploration[26].
2.1 An example of relaxation correlation experiments: T1-T2The pulse sequence for a T1-T2 experiment is the following:
where N is the echo number and the sequence is called IRCPMG since it combines inversion-recovery and the CPMG. The time variables are ta and tb = Nte. The CPMG is used to detect the signal of T2 decay from the end of the T1 recovery period. For a spin species with a specific T1 and T2,the signal is proportional to $[1 - 2\exp ( - {t_a}/{T_1})]\exp ( - {t_b}/{T_2}),$ thus the total signal as a function of ta and tb is
where F(T1,T2) is the probability density of molecules with specific T1 and T2. To obtain F from the data matrix M,a 2D Laplace inversion is needed.
Other 2D experiments have been designed and tested,such as T1-T2 correlation,Diffusion-relaxation correlation,e.g. D-T2 and D-T1,Diffusion-diffusion correlation experiments[16]. Similar to the relaxation-relaxation correlation technique,diffusion can be used for the both dimensions of the 2D experiment. Such experiments can be performed with pulsed field gradient or the static gradients as well as three dimensional extension of these experiments.
3 Theory of 2D NMR of diffusion systemsThe diffusion/relaxation process in porous media follows the Bloch-Torrey equation[27]. However,as shown by Brownstein and Tarr,the diffusion dynamics can be quite complex and the simple idea of pore size distribution may not be sufficient. For example,when pores of different sizes are close,diffusion between the pores will affect the relaxation behavior of both pores. With the application of 2D experiments,one can start to probe the complexity of such diffusion dynamics.
The magnetization [m(r,t)] evolution due to diffusion and relaxation can be studied theoretically[27]:
m is the bulk relaxation rate. Also,the spin precession is not considered here because it is absent during T1 decay and being refocused during CPMG. The general solution can be written as a sum of eigenmodes,
where ji and ti are normalized eigenfunctions and eigenvalues,respectively. The pore boundary behaves as a magnetization sink and the boundary conditions determines the eigenvalues. Both analytical and numerical solutions have been reported in the literature[7, 9, 28, 29, 30] and they describe the full diffusion dynamics and the corresponding NMR behavior[31, 32, 33].
It is important to note that in porous media,relaxation and diffusion behaviors are intimately related. For most of the spins,they have to diffuse to the surface in order to be relaxed. As a result,the measured relaxation,e.g. T2 is not a behavior of a single molecule,but instead the behavior of the eigenmode which is a collection of many molecules with a specific spatial distribution. In the limit of fast diffusion,diffusion is fast to homogenize all spins and thus the relaxation simply reflect pore sizes. However,when diffusion is not fast enough to average all spins,diffusion dynamics can directly influence the NMR data. As a result,the 2D NMR experiments can be used to probe deeper into the microstructure of porous media. Refs. [31, 33, 34, 35] show some of the novel features directly resulted from the diffusion dynamics.
4 ApplicationsThe usefulness of NMR is the ability to measure or infer non-MR knowledge of samples using MR methods. Thus it is crucial to develop the connection between MR results with material properties such as porosity,permeability,composition,fluid-solid interactions,etc. Often such connection is built via a combination of NMR development (e.g. pulse sequence design) and basic physical/chemical research.
Since 2002,MD NMR sequences such as D-T2 and T1-T2 correlation have been used in NMR study of rocks[20, 21] and well-logging systems[26, 36, 37] and contributed to the petroleum exploration. They have also been used in the understanding of food products,measuring the microstructures of dairy and other foods[24, 25],cement hydration and microstructure[23, 38]. Chemical and other exchange mechanisms have been studied using such experiments[18, 22, 39] and recent diffusion correlation experiment using double PFG[40].
One area of rapid development in recent years is the numerical simulation of NMR properties from high-resolution 3D images of X-ray tomography. This is owing in large part to the sophisticated and commercially available X-ray tomography equipment with resolution down to microns. NMR relaxation and diffusion[41, 42] have been simulated including 2D experiments[43]. With the continuous advance in X-ray CT technology in resolution,imaging size and computation power,simulation as well as direct solution of the diffusion problem[9] could become useful for understanding petrophysical measurements.
5 ConclusionThe fields of low-field NMR and MRPM (MR of Porous Media) in particular is ultimately driven by its applications. It is important to stress that it is insufficient to simply borrow methods and technologies developed for other NMR applications. The material complexity as well as the unique deployment requirement deserve dedicated R&D (Research and Development) for this field. This development will inevitably include understanding the basic physics and chemistry of the materials (e.g. Ref. [44]),innovative NMR methods (e.g. Refs. [45, 46]),and new hardware and electronics specifically designed for individual applications. For example the recent report of the high-performance silicon chip NMR spectrometer[47] could be important for miniaturization of NMR system.
Acknowledgement: We thank Prof. Pei-xuan Wang for her help with the abstract translation.| [1] | Dullien F A L. Porous Media:Fluid Transport and Pore Structure[M]. New York:Academic Press, 1991. |
| [2] | Abragam A. The Principles of Nuclear Magnetic Resonance[M]. Oxford:Clarendon, 1961. |
| [3] | Freed D, Burcaw L, Song Y Q. Scaling laws for diffusion coefficients in mixtures of alkanes[J]. Phys Rev Lett, 2005, 94:067602. |
| [4] | Freed D. Dependence on chain length of NMR relaxation times in mixtures of alkanes[J]. J Chem Phys, 2007, 126:174502. |
| [5] | Bloch F. Nuclear relaxation in gases by surface catalysis[J]. Phys Rev, 1951, 83(5):1 062-1 063. |
| [6] | Cohen M H, Mendelson K S. Nuclear magnetic relaxation and the internal geometry of sedimentary rocks[J]. J Appl Phys, 1982, 53:1 127-1 135. |
| [7] | Brownstein K R, Tarr C E. Importance of classical diffusion in NMR studies of water in biological cells[J]. Phys Rev A, 1979, 19:2 446-2 453. |
| [8] | Song Y Q, Zielinski L, Ryu S. Two-dimensional NMR of diffusion systems[J]. Phys Rev Lett, 2008, 100(24):248002. |
| [9] | de Hoop T, Prange M D. Variational analysis of the natural decay rates and eigenmodes of cavity-enclosed diffusive fields[J]. J Phys A:Mathematical and Theoretical, 2007, 40(41):12 463-12 477. |
| [10] | Packer K J, Rees C. Pulsed NMR studies of restricted diffusion. I. Droplet size distributions in emulsions[J]. J Colloid Interf Sci, 1972, 40(2):206-218. |
| [11] | Van den Enden J C, Waddington D, Van Aalst H, et al. Rapid determination of water droplet size distributions by PFG-NMR[J]. J Colloid Interf Sci, 1990, 140(1):105-113. |
| [12] | Mitra P P, Sen P N, Schwartz L M, et al. Diffusion propagator as a probe of the structure of porous media[J]. Phys Rev Lett, 1992, 68:3 555-3 558. |
| [13] | Latour L L, Mitra P P, Kleinberg R L, et al. Time-dependent diffusion coefficient of fluids in porous media as a probe of surface-to-volume ratio[J]. J Magn Reson, Ser A, 1993, 101:342-346. |
| [14] | Sen P N. Time-dependent diffusion coefficient as a probe of geometry[J]. Concept Magn Reson Part A, 2004, 23A(1):1-21. |
| [15] | Grebenkov D. NMR survey of the reflected brownian motion[J]. Rev Mod Phys, 2007, 79(3):1 077-1 137. |
| [16] | Song Y Q. Magnetic resonance of porous media (MRPM):A perspective[J]. J Magn Reson, 2013, 229:12-24. |
| [17] | English A E, Whittall K P, Joy M L G, et al. Quantitative two-dimensional time correlation relaxometry[J]. Magn Reson Med, 1991, 22:425-434. |
| [18] | Lee J H, Labadie C, Springer Jr C S, et al. Two-dimensional inverse laplace transform nmr:Altered relaxation times allow detection of exchange correlation[J]. J Am Chem Soc, 1993, 115:7 761-7 764. |
| [19] | Song Y Q, Venkataramanan L, Hurlimann M D, et al. T1-T2 correlation spectra obtained using a fast two-dimensional laplace inversion[J]. J Magn Reson, 2002, 154:261-268. |
| [20] | Hürlimann M D, Flaum M, Venkataramanan L, et al. Diffusion-relaxation distribution functions of sedimentary rocks in different saturation states[J]. Magn Reson Imaging, 2003, 21:269-277. |
| [21] | Mutina A, Hurlimann M. Correlation of transverse and rotational diffusion coefficient:A probe of chemical composition in hydrocarbon oils[J]. J Phys Chem A, 2008, 112(15):3 291-3 301. |
| [22] | Hubbard P L, McGrath K M, Callaghan P T. A study of anisotropic water self-diffusion and defects in the lamellar mesophase[J]. Langmuir, 2005, 21:4 340-4 346. |
| [23] | Monteilhet L, Korb J P, Mitchell J, et al. Observation of exchange of micropore water in cement pastes by two-dimensional T2-T2 nuclear magnetic resonance relaxometry[J]. Phys Rev E, 2006, 74(6):061404. |
| [24] | Hurlimann M, Burcaw L, Song Y Q. Quantitative characterization of food products by two-dimensional D-T2 and T1-T2 distribution functions in a static gradient[J]. J Colloid Interf Sci, 2005, 297:303-311. |
| [25] | Hills B. Applications of low-field NMR to food science[J]. Annu Rep NMR Spectros, 2006, 58:177-230. |
| [26] | Hürlimann M D, Venkataramanan L, Flaum C, et al. Diffusion-editing:new NMR measurement of saturation and pore geometry//43rd Annual SPWLA meeting[C]. Oiso, Japan:2002. p. paper FFF. |
| [27] | Torrey H C. Bloch equations with diffusion terms[J]. Phys Rev, 1956, 104:563-565. |
| [28] | Kac M. Can one hear the shape of a drum[J]? Am Math Monthly, 1966, 73:1. |
| [29] | Sridhar S, Kudrolli A. Experiments on not "hearing the shape" of drums[J]. Phys Rev Lett, 1994, 72:2 175-2 178. |
| [30] | Grebenkov D S. Laplacian eigenfunctions in NMR. I. A numerical tool[J]. Concept Magn Reson Part A, 2008, 32A(4):277-301. |
| [31] | Cho H, Song Y Q. NMR measurement of the magnetic field correlation function in porous media[J]. Phys Rev Lett, 2008, 100(2):025501. |
| [32] | Bytchenkoff D, Rodts S. Structure of the two-dimensional relaxation spectra seen within the eigenmode perturbation theory and the two-site exchange model[J]. J Magn Reson, 2011, 208(1):4-19. |
| [33] | Song Y Q, Carneiro G, Schwartz L M, et al. Experimental identification of diffusive coupling using 2D NMR[J]. Phys Rev Lett, 2014, 113:235503. |
| [34] | Schwartz L M, Johnson D L, Mitchell J, et al. Modeling two-dimensional magnetic resonance measurements in coupled pore systems[J]. Phys Rev E, 2013, 88(3):032813. |
| [35] | Johnson D L, Schwartz L M. Analytic theory of two-dimensional NMR in systems with coupled macro- and micropores[J]. Phys Rev E, Statistical, Nonlinear, and Soft Matter Physics, 2014, 90(3):032407. |
| [36] | Hürlimann M D. Well Logging//Encyclopedia of Magnetic Resonance[M]. Wiley, 2012. 1-10. |
| [37] | Song Y Q. Focus on the physics of magnetic resonance on porous media[J]. New J Phys, 2012, 14(5):055017. |
| [38] | McDonald P J, Korb J P, Mitchell J, et al. Surface relaxation and chemical exchange in hydrating cement pastes:A two-dimensional nmr relaxation study[J]. Phys Rev E, 2005, 72(1):011409. |
| [39] | Washburn K E, Callaghan P T. Tracking pore to pore exchange using relaxation exchange spectroscopy[J]. Phys Rev Lett, 2006, 97(17):175502. |
| [40] | Paulsen J L, Song Y Q. Two-dimensional diffusion time correlation experiment using a single direction gradient[J]. J Magn Reson, 2014, 244:6-11. |
| [41] | Arns C H. A comparison of pore size distributions derived by nmr and x-ray-ct techniques[J]. Physica A, 2004, 339:159-165. |
| [42] | Arns C H, Sheppard A, Sok R, et al. NMR petrophysical predictions on digitized core images[J]. Petrophysics, 2007, 48(3):202-221. |
| [43] | Arns C H, AlGhamdi T, Arns J Y. Numerical analysis of nuclear magnetic resonance relaxation-diffusion responses of sedimentary rock[J]. New J Phys, 2011, 13:015004. |
| [44] | d'Agostino C, Mitchell J, Mantle M D, et al. Interpretation of NMR relaxation as a tool for characterising the adsorption strength of liquids inside porous materials[J]. Chem-Eur J, 2014, 20(40):13 009-13 015. |
| [45] | d'Eurydice M N, Galvosas P. Measuring diffusion-relaxation correlation maps using non-uniform field gradients of single-sided NMR devices[J]. J Magn Reson, 2014, 248(C):137-145. |
| [46] | Liu H, d'Eurydice M N, Obruchkov S, et al. Determining pore length scales and pore surface relaxivity of rock cores by internal magnetic fields modulation at 2 MHz NMR[J]. J Magn Reson, 2014, 246(C):110-118. |
| [47] | Ha D, Paulsen J L, Sun N, et al. Scalable NMR spectroscopy with semiconductor chips[J]. Proceedings of the National Academy of Sciences, 2014, 111(33):11 955-11 960. |
 2015, Vol. 32
2015, Vol. 32