波谱学杂志  2015, Vol. 32 Issue (1): 67-77
|
代谢组学一般被认为是研究生物体系受到外部与内部因素刺激产生内源性代谢变化的科学[1].Nicholson等人在1999年提出的代谢组学概念其意义表述为：对生物系统因病理生理或基因改变等刺激所致动态多参数代谢应答的定量测定[2, 3].这个过程中代谢物本身又处于生物系统生化活动调控的末端，因此代谢物中包含了被称为生物标记物的信息，分析这样的生物标记物可以得到有关生理表型的结论.为了准确快速全面的找到这样的生物标记物，代谢组学分析中常用的检测手段有核磁共振(NMR)、质谱(MS)技术等[4]，主要研究对象多为生物体液如尿液、血浆等.其中NMR对样本在无破坏性、无选择性的情况下进行分析1H NMR与液相色谱/磁共振联用(LC/NMR)多在代谢组学领域加以应用.然而由于实际生物样本成分的复杂性与NMR方法所具有的较高分辨率，使得最后得到的谱图有非常多的共振峰，这导致研究人员很难从中获取有效信息.为了从这样的复杂信息中识别复杂系统，采取有效的模式识别方法在后期的数据处理中尤为重要.
文献[5]提到了NMR在生物医学中用到的常用模式识别方法[6, 7]，包括无监督方法与监督方法.无监督方法针对的是不利用或无样本所属类别信息的情况，通过数据缩减与识别模式将复杂数据降低至低维空间便于分析.常见无监督方法包括非线性影射法(non-linear mapping, NLM)，层次聚类方法(hierarchical cluster analysis, HCA)，主成分分析(principle component analysis, PCA)等.监督方法需要利用已知的训练样本的分类情况来得到数据分类模型，再利用这个模型对考察数据进行预测和分析.常见的监督方法有偏最小二乘法(partial least squares, PLS)，线性判别法(linear discriminant analysis, LDA)，K-最近邻法(K-nearest neighbor analysis, KNN)，神经网络(neural networks, NN)等.这些方法并不完全局限于分类与识别，其本身还有这模型选择[8]的作用，如K-最近邻方法、决策树方法、支持向量机方法等，使得模型的认识与考察的结论的评价更为详尽与全面.由此可见在代谢组学方法中，面对复杂的数据采取合适的数据分析和模式识别[9]方法，可大大减小工作量并提高分析精度.
近年来支持向量机方法(SVM)[10-12]也开始逐渐应用到代谢组学的研究分析中，以其优良的判别分析手段与预测精度正逐渐被大家所接受.而利用SVM方法分析血吸虫感染代谢产物的研究还没有很多的文献可以参考，本文主要讨论了L1支持向量机方法(L1-norm SVM)在代谢组学分析中的应用.研究背景是文献[13]中对小鼠在受到日本血吸虫感染初期前5周的生物体液与肝脏组织利用1H NMR谱方法进行分析，发现尿样中3-脲基丙酸，一种尿嘧啶代谢产物受到感染的显著影响.我们并不对其生化过程进行详细分析，而是就其数据分析方法用L1-norm SVM进行了讨论与改进，以此探讨L1-norm SVM在代谢组学方面的可行性.
文献[13]对日本血吸虫感染后相关的代谢变量进行了讨论，除了使用PCA方法观察小鼠尿液与血浆样本随感染的时间变化与代谢产物的变化情况，重点在于使用了O-PLS判别分析方法，用于区分代谢情况与哪些种类的代谢物相联系.事实上PCA处理数据时为了保证信息损失最小，需要利用交叉验证来确定得到使用多少PC来描述数据集合.支持向量机方法不但可以实现聚类，还可实现特征选择功能，这样的操作实际上可通过支持向量机方法一次性解决，从而节省很多工作.这也是本文研究的重要原因之一.
1 数据处理方法 1.1 偏最小二乘与隐结构正交投影 1.1.1 偏最小二乘回归(partial least squares, PLS)偏最小二乘法[14, 15]与PCA有类似之处[16]，二者均需要提取反映数据变动的最大信息，不同之处是PCA只分析一个自变量矩阵，而PLS需要分析自变量矩阵与响应变量矩阵，同时PLS具有预测功能.
Xn×m为输入变量，Yn×k为响应变量，其中n表示样本个数，且它们均为中心化后的数据，均值为0.w1为输入变量的第1个投影方向，v1是响应变量的第一个投影方向，因此Xw1是X在w1方向上的投影，Yv1是Y在v1方向上的投影.PLS的目的就是求出w1与v1使得r(Xw1, Yv1)，Var(Xw1)，Var(Yv1)三者都尽可能大.其中带入方差与协方差的计算公式，得
| $ \begin{array}{l} \max \;\;\;\;\;v{'_1}Y'X{w_1}\\ s.t.\;\;\;\;\;\;{\rm{ }}w{'_1}{w_1} = 1\\ \;\;\;\;\;\;\;\;\;\;\;v{'_1}{v_1} = 1 \end{array} $ | (1) |
对此问题通过引入Lagrange函数.求出w1与v1后设t1=Xw1，u1=Yv1，因此t1与u1就是X，Y分别在w1与v1方向的投影.用t1分别对X和Y做拟合回归，得到回归系数
| $ \begin{array}{l} {X^{(1)}} = X-{t_1}p{'_1} = X-X{w_1}p{'_1}\\ {Y^{(1)}} = Y-{t_1}r{'_1} = Y - X{w_1}r{'_1} \end{array} $ | (2) |
然后将X(1)与Y(1)作为上一步的X与Y，利用上述相同的分析，可得到第2个投影方向w2同样进行分析.最终得到类似如下形式的表达式：
| $ \begin{array}{l} X = {t_1}p{'_1} + {t_2}p{'_2} + {t_3}p{'_3} + \cdots {t_A}{{p'}_A} + E\\ Y = {t_1}r{'_1} + {t_2}r{'_2} + {t_3}r{'_3} + \cdots {t_A}{{r'}_A} + F \end{array} $ | (3) |
至此就得到了PLS的计算结果，A的大小表示(3)式中成分的个数.其中E与F是提取潜变量后X与Y的残差.通常情况下只考察前两个成分(A=2).
1.1.2 隐结构正交投影(Orthogonal Projections to Latent Structures, O-PLS)隐结构正交投影(Orthogonal Projections to Latent Structures, O-PLS)是Johan Trygg等人[18]提出的.O-PLS的主要思想是在PLS分析之前，先对原始变量进行正交校正，剔除输入变量中与响应变量正交的一些部分.这样的做法相当于对PLS分析中与响应变量无关的输入变量进行剔除，减小了模型的复杂度.
具体方法[19]如下：首先寻找一系列投影方向，使得原变量投影后得到的新向量（正交向量）与其响应变量正交；然后用正交向量回归拟合原来的输入变量，得到输入变量的拟合值，最后用原来输入变量减去其用正交向量得到的拟合值就得到了正交校正之后的输入变量.本文在使用偏最小二乘法之前利用此方法先对数据进行了预处理.
1.2 基于L1范数的支持向量机(L1-norm SVM)方法1H NMR得到的数据所表征的特征是如此之多，一般情况下我们将其看作多类型问题进行特征选择与模式识别[8]，已经熟知的方法如判别分析法(Discriminant analysis)[20]、回归与决策树方法(regression and decision trees)都属于这个类型.其他类型的方法包括One-versus-the-rest(one versus all)方法[21]，配对比较方法(pairwise comparison)[22]，纠错输出编码方法(error-correcting output coding)[23]与多目标方法(multiclass objective functions)[24]等.
举例而言，若考虑多类型分类中一个常用的方法“one versus all”(OVA)，是从剩余的大类中逐次提取单个类直到结束.但这样的做法有着潜在的风险：首先，它有次序的对二元分类进行了训练，当有很多个类时，每个二元分类变得非常不平衡且在在单个类上有极小的分岔，使得有较小分支的类趋向于被忽略；其次，OVA认为单个变量如果被分入某个二元分类，那么它与其他所有类均有联系，这显然是过于主观的认识；第三，如果不存在一个明显占主要地位的类，那么OVA方法会失效.而L1-norm SVM方法很好的规避了这些风险[25].
与L2-norm SVM相比，L1-norm SVM有不同的应用范围，L1惩罚项[26]允许当一个模型的变量数p远大于样本大小n时仍可以有效被控制，同时L1-norm SVM中输入输出变量的联合分布在分类中起到了很重要的作用.因此就这些方面而言，L1-norm SVM有效遏制了分类中的维数灾难，提供了一个通过L1惩罚项，可以给出决定函数相对稀疏的表达方式[27].
有研究[28]表明L1-norm SVM在某些条件下可以表现出更好的性质，如存在冗余噪声特征（噪声为标准正态噪声）时，L1-norm SVM的效果会比L2-norm SVM更好，且从获得的样本条件来看，样本采集过程中的确存在较大的噪声特征，因此更倾向于L1-norm SVM.以下将对L1-norm SVM进行详细说明.
对常见的k类问题，已知输入为
| $ \begin{array}{l} \mathop {\min }\limits_{{w_c}, {b_c};c = 1, \cdots, k} {n^{- 1}}\sum\limits_{i = 1}^n {{{\{ 1- \mathop {\min }\limits_c [{f_{{y_i}}}({x_i})-{f_c}({x_i})]\} }_ + }} \\ \sum\limits_{c = 1}^k {||{w_c}|{|_1} \le s, {\rm{ }}} \sum\limits_{c = 1}^k {{w_c} = 0, {\rm{ }}\sum\limits_{c = 1}^k {{b_c}{\rm{ = 0 }}} } \end{array} $ | (4) |
对(4)式进行简要说明，得到本文使用的标准二元分类问题如下.给定一个训练样本
| $ \begin{array}{l} \mathop {\min }\limits_{{\beta _0}, \beta } \sum\limits_{i = 1}^n {\{ 1- {y_i}{{[{\beta _0} + \sum\limits_{j = 1}^q {{\beta _j}{h_j}({x_j})]} \} }_ + }} \\ s.t.{\rm{ }}||\beta |{|_1} = |{\beta _1}| + \cdots + |{\beta _q}| \le s \end{array} $ | (5) |
其中s是调节参数，问题的解依赖于
| $ \hat f(x) = {\hat \beta _0} + \sum\limits_{j = 1}^q {{{\hat \beta }_j}{h_j}(x)} $ | (6) |
为了求解此问题，利用Lagrange法求解如下等价问题[29]：
| $ \mathop {\min }\limits_{{\beta _0}, \beta } \sum\limits_{i = 1}^n {{{\{ 1- {y_i}[{\beta _0} + \sum\limits_{j = 1}^q {{\beta _j}{h_j}({x_j})}]\} }_ + }} + \lambda ||\beta |{|_1} $ | (7) |
因此分类结果由
从这里看出，通过最优化方法可以解出L1-norm SVM方法中需要的最优解，从而进行相应的分类.
2 L1-norm SVM方法在代谢组学中的应用 2.1 数据来源说明本文采用的数据是由文献[13]中研究人员提供的，同样是由1H NMR处理得到感染后的代谢数据，但与文献[13]的时间周期不同，这里所处理的实验数据是小鼠感染了血吸虫后第6周~8周的数据.具体的处理方法是对得到的数据先用与文献[13]一致的O-PLS方法得到谱[30]，然后对同样周期的数据采用L1-norm SVM方法再次分析，比较并分析得到L1-norm SVM方法与原文采用的O-PLS方法的区别.
2.2 数值分析结果第6周NMR数据利用O-PLS分析得到的谱与利用L1-norm SVM得到的谱结果如图 1.
|
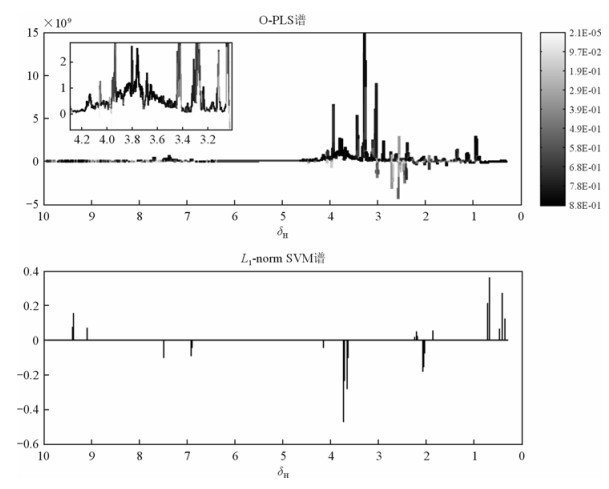
| 图 1 第6周尿液代谢物1H NMR数据的O-PLS谱与L1-norm SVM谱.图右侧的灰度色块是相关系数标度 Fig. 1 The O-PLS and L1-norm SVM spectra of urinary 1H NMR data in sixth week. Gray scale chart on the right side of the diagram is the correlation coefficient |
图 1中给出了小鼠感染日本血吸虫后第6周的代谢组分1H NMR谱.显然的我们关心的是如O-PLS谱所示的深色部分代表的成分，因为这些深色位置代表了由于感染而有显著变化的代谢组分.从图中可以看出，深色的密集区域，就横坐标来看分别有3.73，3.65，0.72，0.68，2.07在L1-norm SVM谱中很好的被检测出来.
|
| 图 2 第7周尿液1H NMR数据的O-PLS谱与L1-norm SVM谱.图右侧的灰度色块是相关系数标度 Fig. 2 The O-PLS and L1-norm SVM spectra of urinary 1H NMR data in seventh week. Gray scale chart on the right side of the diagram is the correlation coefficient |
|
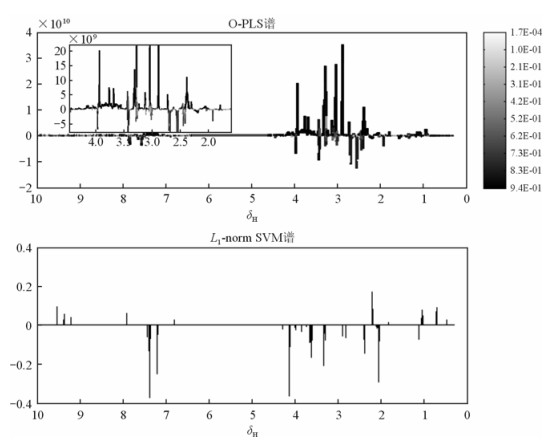
| 图 3 第8周尿液1H NMR数据的O-PLS谱与L1-norm SVM谱.图右侧灰度色块是相关系数标度 Fig. 3 The O-PLS and L1-norm SVM spectra of urinary 1H NMR data in eighth week. Gray scale chart on the right side of the diagram is the correlation coefficient |
图 1~图 3中横坐标均代表化学位移，不同的化学位移代表不同的组分.O-PLS谱用灰度标尺表示相关性强弱，相关性越低，颜色越浅；相关性越高颜色越深，谱分析中重点考察的就是这些谱分析中特征突出位置的组分.表 1中所示为第6周~8周间L1-norm SVM所检验出相关性较大的部分组分（不同组分对应不同的化学位移），与O-PLS谱比较，这些组分均为O-PLS谱中相关性较大的组分：第6周所示的化学位移表示O-PLS谱中相关性在6.8E-01~8.8E-01的高相关性组分；第7周中所示的化学位移表示O-PLS谱中相关性在6.1E-01~7.9E-01之间的高相关性组分；第8周中的化学位移是O-PLS谱中相关性在7.3E-01~9.4E-01之间的组分，其中第8周数据在7附近的相关性在6.2E-01~7.3E-01之间.
| Metabolites(key) | 6 weeks* | 7 weeks | 8 weeks |
| 1 | 3.91** | 4.13 | 7.20, 7.31, 7.37, 7.55 |
| 2 | 3.72~3.73 | 3.98, 3.72 | 4.11~4.13 |
| 3*** | 3.63, 3.64, 3.65 | 3.65, 3.62 | 3.84, 3.60~3.65 |
| 4 | 2.07~2.08 | 2.07~2.08 | 3.30 |
| 5 | 2.04~2.05 | 2.04~2.05 | 2.90 |
| 6 | 0.72, 0.70, 0.68 | 1.01, 0.99 | 2.38 |
| 7 | 0.81, 0.70, 0.65 | 2.04, 2.06 | |
| 8 | 0.47~0.48, 0.43~0.44 | 1.15 | |
| *此列为小鼠感染后第6周的数据.后两列同样小鼠感染7周与8周的数据； **尿液代谢物的化学位移； ***指的是代谢物编号 | |||
L1-norm SVM谱将O-PLS谱中我们需要的组分用简洁准确的方式呈现出来，如第8周谱中，O-PLS谱中相关性从8.5E-05~3.5E-01所代表的冗余成分占了绝大部分，若希望快速准确的得到高相关性组分位置，显然需要花较多时间在过滤低相关度组分上，容易丢失重要数据，也增加了工作量，同时对所关心的部分造成了干扰.反之，从L1-norm SVM谱中可以看出，重要相关性部分是通过准确的杆状图标注出来的，很好的克服了O-PLS中大量非重点研究数据的影响.
注意O-PLS谱中不是所有的深色区域都代表代谢异常的代谢物，而是在这些深色区域中所属的代谢物可能存在代谢异常，仅从数据出发，深色区域未检验的这个不属于分类失误，而是我们能挑出代谢异常最显著的那个代谢物，因此没有完全检测所有深色区域的每个代谢物.
同时在L1-norm SVM谱中标注出有显著性的位置在O-PLS谱中表现为低相关性，但就实际情况而言这些较弱相关性的位置并不一定不具有显著性差异，仅是因为它们的变化趋势与O-PLS的第一主成分相关性小.也有可能因为背景噪声或者代谢组分本身变化剧烈但变化区间较小，造成感染后此代谢物的异常程度不够明显.因此这些L1-norm SVM标注出来的这些异常点可能是需要我们更详尽考察的部位，是否属于误分仍然需要实验并进一步讨论.
3 结论从比较中可以看出，L1-norm SVM方法完全地表达出了O-PLS中关于代谢组分对类间差异显著性的贡献，更切实且精确地找出了感染后代谢活动表现更显著特征的代谢组分.
从分类结果上来看，L1-norm SVM谱首先很好的得到了O-PLS分析方法得到的结果.在第8周（图 3）中感染后代谢成分明显突出的组分在L1-norm SVM谱中均有明显的检测（表 1）.作为在血吸虫代谢组学中尚未有普遍应用的L1-norm SVM方法而言，实际测试的效果令人满意.
在分类得到这样的结果后，我们就可以对得到的突出代谢组分进行重点研究.感染后代谢组分的动态变化对我们防止血吸虫病有着至关重要的作用，L1-norm SVM方法为代谢组分的研究带来了新的方向与思考途径，是有实用价值和可操作性的分析方法.
| [1] | Guo Bin(郭宾), Dai Ren-ke(戴仁科) . Current trends in analytical methodologies and experimental strategies for metabonomics(代谢组学及其研究策略和分析方法进展)[J]. Chinese Journal of Health Laboratory Technology(中国卫生检验杂志) , 2007, 17 (3) : 554-563 |
| [2] | Tang Hui-ru(唐惠儒), Wang Yu-lan(王玉兰) . Metabonomics(代谢组研究)[J]. Chinese Bulletin of Life Sciences(生命科学) , 2007, 3 : 272-280 |
| [3] | Nicholson J K, Lindon J C, Holmes E . 'Metabonomics': understanding the metabolic responses of living systems to pathophysiological stimuli via multivariate statistical analysis of biological NMR spectroscopic data[J]. Xenobiotica , 1999, 29 (11) : 1 181-1 189 DOI:10.1080/004982599238047 |
| [4] | Xu Guo-wang(许国旺), Yang Jun(杨军) . Recent advances in metabonomics(代谢组学及其研究进展)[J]. Chinese Journal of Chromatography(色谱) , 2003, 21 (4) : 316-320 |
| [5] | Qiu Yu-jie(邱玉洁), Xia Sheng-an(夏圣安), Ye Chao-hui(叶朝辉) et al . Pattern recognition methods in biomedical magnetic resonance(生物医学核磁共振中的模式识别方法)[J]. Chinese J Magn Reson(波谱学杂志) , 2005, 22 (1) : 99-111 |
| [6] | Hastie T, Tibshirani R, Friedman J et al . The elements of statistical learning: data mining, inference and prediction[J]. The Mathematical Intelligencer , 2005, 27 (2) : 83-85 |
| [7] | Bradley P S, Mangasarian O L . Feature selection via concave minimization and support vector machines[J]. International Council for Machinery Lubrication , 1998, 98 : 82-90 |
| [8] | Li T, Zhang C L, Ogihara M . A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression[J]. Bioinformatics , 2004, 20 (15) : 2 429-2437 DOI:10.1093/bioinformatics/bth267 |
| [9] | Guyon I, Elisseeff A . An introduction to variable and feature selection[J]. The Journal of Machine Learning Research , 2003, 3 : 1 157-1 182 |
| [10] | Zhang Xue-Gong(张学工) . Introduction to statistical learning theory and support vector machines(关于统计学习理论与支持向量机)[J]. Acta Automatica Sinica(自动化学报) , 2000, 26 (1) : 32-42 |
| [11] | Chang C C, Lin C G . LIBSVM: A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology(TIST) , 2011, 2 (3) : 27-66 |
| [12] | Guan W, Zhou M, Hampton C Y et al . Ovarian cancer detection from metabolomic liquid chromatography/mass spectrometry data by support vector machines[J]. BMC Bioinformatics , 2009, 10 (1) : 259-274 DOI:10.1186/1471-2105-10-259 |
| [13] | Wu J F, Xu W X, Ming Z P et al . Metabolic changes reveal the development of schistosomiasis in mice[J]. PLoS Neglected Tropical Diseases , 2010, 4 (8) : e807-818 DOI:10.1371/journal.pntd.0000807 |
| [14] | Haaland D M, Thomas E V . Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information[J]. Anal Chem , 1988, 60 (11) : 1193-1202 DOI:10.1021/ac00162a020 |
| [15] | Tobias R D . An introduction to partial least squares regression[J]. Proc. Ann. SAS Users Group Int. Conf , 1995, 20 : 2-5 |
| [16] | Barker M, Rayens W . Partial least squares for discrimination[J]. J Chemometr , 2003, 17 (3) : 166-173 DOI:10.1002/(ISSN)1099-128X |
| [17] | Rosipal R, Trejo L J . Kernel partial least squares regression in reproducing kernel hilbert space[J]. The Journal of Machine Learning Research , 2009, 2 : 97-123 |
| [18] | Trygg J, Wold S . Orthogonal projections to latent structures (O-PLS)[J]. J Chemometr , 2002, 16 (3) : 119-128 DOI:10.1002/(ISSN)1099-128X |
| [19] | Bylesj M, Rantalainen M, Nicholson J K et al . K-OPLS package: Kernel-based orthogonal projections to latent structures for prediction and interpretation in feature space[J]. BMC Bioinformatics , 2008, 9 (1) : 106-113 DOI:10.1186/1471-2105-9-106 |
| [20] | Tibshirani R, Hastie T, Narasimhan B et al . Diagnosis of multiple cancer types by shrunken centroids of gene expression[J]. Proc Natl Acad Sci USA , 2002, 99 (10) : 6 567-6 572 DOI:10.1073/pnas.082099299 |
| [21] | Smola A J, Sch lkopf B . A tutorial on support vector regression[J]. Statistics and Computing , 2004, 14 (3) : 199-222 DOI:10.1023/B:STCO.0000035301.49549.88 |
| [22] | Friedman J, Hastie T, Tibshirani R . Special invited paper additive logistic regression: A statistical view of boosting[J]. Annals of Statistics , 2000 (2) : 337-374 |
| [23] | Allwein E L, Schapire R E, Singer Y . Reducing multiclass to binary: A unifying approach for margin classifiers[J]. J Mach Learn Res , 2001 (1) : 113-141 |
| [24] | Weston J, Watkins C. Technical Report CSD-TR-98-04 Multi-Class Support Vector Machines[C]. London: University of London, 1998. |
| [25] | Wang L, Shen X . On L1-norm multiclass support vector machines[J]. J Am Stat Assoc , 2007, 102 (478) : 583-594 DOI:10.1198/016214506000001383 |
| [26] | Wang Ding-cheng(王定成), Fang Ting-jian(方廷健), Tang Yi(唐毅) et al . Review of support vector machines regression theory and control(支持向量机回归理论与控制的综述)[J]. Pattem Recognition and Aitificial Intelligence(模式识别与人工智能) , 2003, 16 (2) : 192-197 |
| [27] | Yu H, Kim S . SVM Tutorial: Classification, regression and ranking[J]. Handbook of Natural Computing. Springer Berlin Heidelberg , 2012, 2 : 479-506 |
| [28] | Zhu J, Rosset S, Hastie T, Tibshirani R . 1-norm support vector machines[J]. Advances in Neural Information Processing Systems , 2004 (1) : 49-56 |
| [29] | Hastie T, Rosset S, Tibshirani R et al . The entire regularization path for the support vector machine[J]. J Mach Learn Res , 2004 (5) : 1 391-1 415 |
| [30] | Kang J, Choi M Y, Kang S et al . Application of a 1H nuclear magnetic resonance (NMR) metabolomics approach combined with orthogonal projections to latent structure-discriminant analysis as an efficient tool for discriminating between Korean and Chinese herbal medicines[J]. J Agr Food Chem , 2008, 56 (24) : 11 589-11 595 DOI:10.1021/jf802088a |
表1(Table 1)
