文章信息
- 金亚莹, 陈志伟
- JIN Ya-ying, CHEN Zhi-wei
- 一种新的DEPT谱编辑方法
- A New DEPT Spectral Editing Method
- 波谱学杂志, 2015, 32(1): 59-66
- Chinese Journal of Magnetic Resonance, 2015, 32(1): 59-66
- http://dx.doi.org/10.11938/cjmr20150107
-
文章历史
收稿日期: 2014-06-12
收修改稿日期: 2015-01-09


DOI:10.11938/cjmr20150107
无畸变极化转移增益法(Distortionless Enhancement by Polarization Transfer,DEPT)[1],在提高低旋磁比的核灵敏度方面以及简化13C NMR波谱解析方面具有重大的应用价值[2, 3].DEPT一般有3张子谱,分别是照射1H的第3个脉冲的翻转角等于45°、90°和135°时得到的.理论上,45°谱中,CH3、CH2及CH均为正信号;90°谱中,只有CH的信号;135°谱中,CH3和CH为正信号,CH2为负信号.用户可以通过对DEPT谱图的肉眼观察,依靠理论知识和个人经验,判断谱图中CHn各个子谱的情况.此方法无法快速准确地得出结论,当遇到复杂和密集谱线时误判率也比较高.
如果能够分离出纯净的CHn信号子谱,用户就能够直接从谱图中获得有用信息,这对复杂和密集的碳谱线的解析有重要意义.为了解决上问题,一种方法是从脉冲序列上对DEPT实验进行改进.此类改进实验有很多,比如2000年,丁克洋提出两种新的DEPT脉冲序列:DEPT-90-45和DEPT-90+45[4, 5];Roher等人在2002年提出用于固体NMR的DEPT新序列[6].另一种方法是对DEPT谱图进行谱编辑,以分离出纯净的CHn信号子谱.现有的谱编辑方法主要有两种.第1种是使用理论或经验公式对谱图进行计算.由于实验数据与理论值都会有所偏差,使用理论或经验公式无法很好地去除杂信号,影响判断;第2种是使用Bendall等人提出的基于一元线性回归计算的DEPT谱编辑法[1, 7].该方法相比于使用理论公式的谱编辑结果有所改善,但各CHn子谱中仍然存在杂信号的残留,不利于复杂化合物的谱分析.
为了解决DEPT谱编辑后残留杂信号较多的问题,本文提出一种新的DEPT谱编辑技术,对谱图数据进行多元线性回归计算,有效地分离出CH3、CH2、CH的谱峰信号,方便用户作出迅速准确的判断.通过实验对比表明,使用新方法编辑后的各CHn子谱图更加的纯净易分辨.
1 研究背景DEPT谱是通过改变照射1H的第3个脉冲的翻转角θ,使其作45°、90°和135°变化得到的.由理论计算可知,CHn信号强度与翻转角θ的关系满足(1)~(3)式[1, 7](式中Sx为13C信号横向磁化),变化如图 1所示.
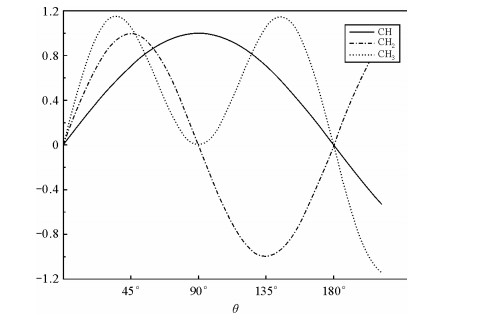
|
| 图 1 CHn各子谱信号与θ角的关系 Fig. 1 The relationship between CHn and θ |
| $ {\rm{CH}}:{S_x}\sin \theta $ | (1) |
| $ {\rm{C}}{{\rm{H}}_{\rm{2}}}:{S_x}\sin 2\theta $ | (2) |
| $ {\rm{C}}{{\rm{H}}_{\rm{3}}}:\frac{3}{4}{S_x}(\sin \theta + \sin 3\theta ) $ | (3) |
从图 1可以看出,当θ1为45°时,CH3、CH2及CH均为正信号;当θ2为90°时,只有CH的信号;当θ3为135°时,CH3和CH为正信号,CH2为负信号.下文将θ1、θ2、θ3的谱图分别记为S(45°)、S(90°)和S(135°).
由上分析可知,在理想情况下S(90°)谱就是CH子谱,S(45°)谱减去S(135°)谱便得到CH2子谱,S(45°)谱加S(135°)谱减去倍的S(90°)谱便得到CH3子谱.可以把这些关系表示如下:
| $ {\rm{CH}} = S(90^\circ ) $ | (4) |
| $ {\rm{C}}{{\rm{H}}_{\rm{2}}} = S(45^\circ )-S(135^\circ ) $ | (5) |
| $ {\rm{C}}{{\rm{H}}_{\rm{3}}} = S(45^\circ ) + S(135^\circ )-\sqrt 2 \times S(90^\circ ) $ | (6) |
但是在现实情况下,同一化合物中的13C-1H偶合常数JCH具有一定的分布范围,脉冲间距1/JCH的取值是平均值,无法跟所有基团匹配,导致S(90°)谱本应该只有CH信号,却出现CH2和CH3信号的残留;另外,θ脉冲不可能有完全的均一性和完整的脉冲周期,CH2、CH3在S(135°)时的绝对信号比S(45°)时的绝对信号稍有减弱.因此根据(4)~(6)式编辑得到的各子谱图会残留较多的杂信号,影响用户对结果的判断.
Bendall等人对拟合公式进行改进,提出(7)~(9)式[1, 7].该方法通过一元线性回归计算谱图的拟合系数x、y、z,然后将系数回代得到拟合方程.第1步,对S(45°)和S(135°)进行寻峰,找出CH和CH3信号峰的峰值,记为S(45°)'和S(135°)'.然后令(7)式等于0,用一元线性回归法对S(45°)'和S(135°)'进行拟合,得到系数y.第2步,对S(45°)、S(90°)、S(135°)进行寻峰,找出CH2和CH3信号峰的峰值,记为S(45°)''、S(90°)''和S(135°)''.令(8)式等于0,用一元线性回归法对S(90°)''和S(45°)''+y×S(135°)''进行拟合,得到系数x.第3步,对S(45°)、S(90°)、S(135°)进行寻峰,找出CH和CH2信号峰的峰值,记为S(45°)'''、S(90°)'''和S(135°)'''.令(9)式等于0,用一元线性回归法对S(45°)'''+y×S(135°)'''和S(90°)'''进行拟合,得到系数z.第4步,将系数x、y、z代入(7)~(9)式就能够得到CHn子谱的计算公式.该方法相对于直接用理论公式计算有所改进,能够针对不同样品进行系数匹配.但是由于拟合时只考虑到两个谱图,导致杂信号消除不完全,效果不是很理想.本文在此基础上,使用多元线性回归优化算法,达到更好的去杂信号的效果.
| $ {\rm{C}}{{\rm{H}}_{\rm{2}}} = S(45^\circ )-y \times S(135^\circ ) $ | (7) |
| $ {\rm{CH}} = S(90^\circ )- x \times [S({\rm{45}}^\circ ) + y \times S({\rm{135}}^\circ )] $ | (8) |
| $ {\rm{C}}{{\rm{H}}_{\rm{3}}} = S(45^\circ ) + y \times S(135^\circ )-z \times S(90^\circ ) $ | (9) |
本文方法的主要特点是使用了多元线性回归对谱数据进行处理.多元线性回归是利用线性回归方程对多个自变量与一个因变量之间关系进行建模的一种回归分析.当一个现象与多个因素相联系时,利用多个自变量的最优组合来预测或估计因变量,这比只用一个自变量进行预测或估计更有效.在现实条件下,影响因素往往是多个,因此,多元线性回归比一元线性回归的实用意义更大.
多元线性回归模型的回归函数如下:
| $ {y_i} = {b_0} + {b_1}{x_{i1}} + {b_2}{x_{i2}} + \cdot \cdot \cdot + {b_p}{x_{ip}} $ | (10) |
多元线性回归的基本思想是根据最小二乘原理,求解b0,b1,b2,…,bp,使全部观测值yi与回归值
| $ Q = \sum\limits_{i = 1}^n {{{({y_i}- {{\hat y}_i})}^2}} = \sum\limits_{i = 1}^n {{{[{y_i}-({b_0} + {b_1}{x_{i1}} + {b_2}{x_{i2}} + \cdot \cdot \cdot + {b_p}{x_{ip}})]}^2}} $ | (11) |
由于残差平方和Q是b0,b1,b2,…,bp的非负二次式,所以(11)式必然存在一个最小值.根据极值原理,当Q取得极值时,应满足:
| $ \frac{{\partial Q}}{{\partial {b_j}}} = 0, \begin{array}{*{20}{c}} {} \end{array}j = 0, \;1, \;2, \; \cdots, \;p $ | (12) |
求解矩阵方程(12)式,可以得到Q取极值情况下的解b0,b1,b2,…,bp.
2.2 新方法实现步骤针对DEPT谱的实际求解过程,利用多元线性回归对DEPT谱编辑进行优化,具体步骤如下:
(1)分离CH2信号
由上文分析知,在S(45°)、S(90°)、S(135°) 3张谱图中都有CH2,在S(135°)中CH2比在S(45°)中有所减弱,而S(90°)中只有很小的CH2残留信号.因此首先考虑分离S(45°)中的CH2.此时,CH和CH3信号就是杂信号,应该用多元线性回归法消除掉.从S(135°)的正向谱线中能够判断出CH和CH3各个峰.通过寻峰,我们可以对应找出S(45°)、S(90°)、S(135°)中CH和CH3的各个峰值,记为S(45°)'、S(90°)'、S(135°)'.令(13)式等于0,将S(45°)'、S(90°)'、S(135°)'代入,利用多元线性回归计算出拟合系数a1、a2,再把a1、a2代入(13)式就得到CH2的拟合公式.用该公式进行谱编辑就能得到只含CH2的谱图.
| $ {\rm{C}}{{\rm{H}}_{\rm{2}}} = S({\rm{45}}^\circ ) + {a_1} \times S({\rm{90}}^\circ ) + {a_2} \times S({\rm{135}}^\circ ) $ | (13) |
(2)分离CH信号
S(90°)谱图中主要是CH信号,但谱图中也会存在CH2和CH3谱线的残余,这些残余相对于CH信号来说就是杂信号.根据(1)~(3)式可以知道,S(90°)中CH的信号相对强度为1,S(45°)中峰的信号相对强度为0.7.比较S(45°)和S(90°)的谱图,可以认为S(90°)谱图中的峰比S(45°)相对应的峰强度高的为CH,反之若强度低则可以看做杂信号.而从S(135°)中的负信号可以确定CH2,正信号中的CH位置和S(90°)的CH位置一样,可以分离出,余下的正信号则为CH3峰.由此从S(135°)能确定CH2和CH3信号峰位置.取出S(45°)、S(90°)、S(135°)的CH2和CH3的峰值,记为S(45°)''、S(90°)''、S(135°)''.令(14)式等于0,将S(45°)''、S(90°)''、S(135°)''代入,利用多元线性回归计算出拟合系数b1、b2,再将b1、b2代入(14)式得到CH的拟合公式.用该公式进行谱编辑就能得到只含CH的谱图.
| $ {\rm{CH}} = {b_{\rm{1}}} \times S({\rm{45}}^\circ ) + S({\rm{90}}^\circ ) + {b_2} \times S({\rm{135}}^\circ ) $ | (14) |
(3)分离CH3信号
同CH2信号一样,CH3信号也是S(45°)谱中的最强,所以考虑分离S(45°)中的CH3.上面两步我们已经找到了CH和CH2谱线的位置,对应找出3张谱图中CH和CH2谱线的峰值,记为S(45°)'''、S(90°)'''、S(135°)'''.令(15)式等于0,将S(45°)'''、S(90°)'''、S(135°)'''代入,利用多元线性回归计算出拟合系数c1、c2.将c1、c2代入(15)式就得到CH3的拟合公式.用该公式进行谱编辑就能得到只含CH3的谱图.
| $ {\rm{C}}{{\rm{H}}_{\rm{3}}} = S({\rm{45}}^\circ ) + {c_1} \times S({\rm{90}}^\circ ) + {c_2} \times S({\rm{135}}^\circ ) $ | (15) |
通过以上步骤,实现了拟合系数的计算以及CHn子谱的分离.
3 实验结果本文选取多种不同的样品进行DEPT谱编辑,均取得了不错的效果.
(1)下面详细介绍对溶于氘代氯仿的2-乙基-1-茚酮样品的DEPT谱编辑.通过对2-乙基-1-茚酮结构式分析可知,该样品的CH3、CH2、CH的个数分别是1、2、5.
分别使用理论公式、Bendall的拟合公式以及DEPT谱编辑新方法对该样品进行谱编辑.使用Bendall的方法计算出的拟合系数为x=0.086 2,y=0.925 0,z=1.380 0.利用我们的DEPT谱编辑新方法对样品进行拟合,得到的拟合系数如表 1所示.
| 基团 | 谱 | ||
| S(45°) | S(90°) | S(135°) | |
| CH | -0.1607 | 1 | 0.1539 |
| CH2 | 1 | 0.7615 | -1.6144 |
| CH3 | 1 | -1.3031 | 0.7960 |
最后得到的谱图如图 2所示.图 2(a)是DEPT原始谱图,从中无法很快判断出CHn子谱信息.理论公式编辑结果[图 2(b)]中的CH2和CH子谱信号存在明显的杂质残留,影响分析判断.使用Bendall公式编辑后[图 2(c)],CH2和CH子谱信号仍然存在杂信号,干扰了对有用信号的判断.而使用新方法编辑后得到的各子谱[图 2(d)]基本没有杂信号,结果较为纯净、易分辨.
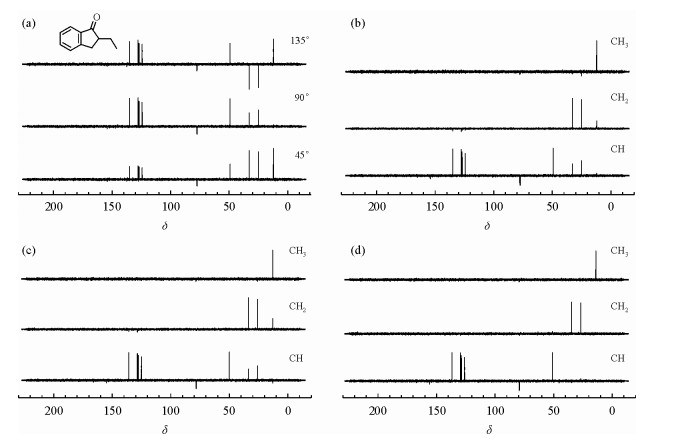
|
| 图 2 (a)溶于氘代氯仿的2-乙基-1-茚酮样品的DEPT原始谱图;(b)理论公式编辑结果;(c) Bendall方法编辑结果;(d)新方法编辑结果 Fig. 2 The DEPT spectra of 2-ethylindanone in CDCl3: (a) original, (b) editing results of theoretical formulae, (c) editing results of Bendall's method, (d) editing results of new method |
(2)本文使用的另一个样品是辛伐他汀的氘代乙腈溶液,辛伐他汀的结构式如图 3(a)插图所示,其CH3、CH2、CH个数分别为5、6、10.用Bendall的方法计算出的拟合系数为x=1.608 9,y=0.039 5,z=1.534 8.用DEPT谱编辑新方法得到的系数如表 2所示.
| 基团 | 谱 | ||
| S(45°) | S(90°) | S(135°) | |
| CH | -0.0793 | 1 | 0.0120 |
| CH2 | 1 | 0.2012 | -1.8493 |
| CH3 | 1 | -1.4644 | 1.4645 |
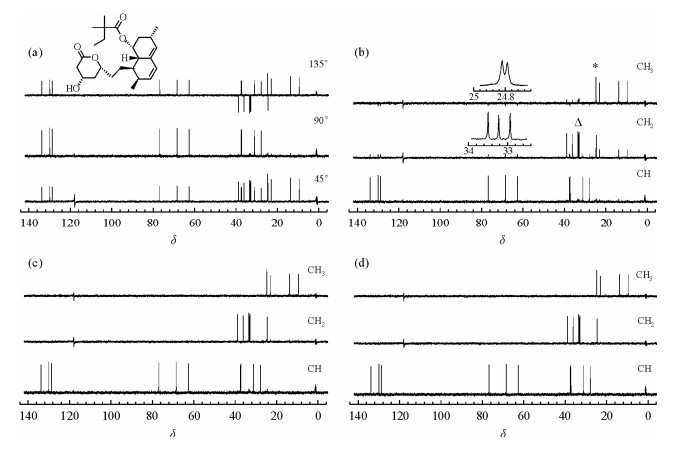
|
| 图 3 (a)溶于氘代乙腈的辛伐他汀样品的DEPT原始谱图;(b)理论公式编辑结果;(c) Bendall方法编辑结果;(d)新方法编辑结果 Fig. 3 The DEPT spectra of simvastatin in CD3CN: (a) original, (b) editing results of theoretical formulae, (c) editing results of Bendall's method, (d) editing results of new method |
分别利用理论公式,Bendall的方法和DEPT谱编辑新方法对辛伐他汀样品的DEPT谱进行谱编辑,结果如图 3所示.图 3(b)的CH3子谱中左边第一个峰(标*位置)放大后是两个峰,CH3子谱一共有5个信号峰,与结构式中有5个CH3相符.CH2子谱中间较密集的峰(标△位置)放大后是3个峰,CH2子谱一共有6个信号峰,与结构式中有6个CH2相符.图 3(c)和图 3(d)同上,此处不再赘述.通过比较可以看出,理论公式编辑结果[图 3(b)]的CH2和CH3子谱有较多的杂信号.Bendall的方法编辑结果[图 3(c)]中CH3子谱的CH3杂信号有所减少,但CH和CH2子谱仍可见杂信号残留.新方法编辑后得到的各子谱[图 3(d)]中杂信号基本上很小,各个CHn信号干净清楚,从中可以很容易判断出CH3、CH2、CH的个数.
通过以上对比实验表明,相比于使用理论公式,本文提出的方法针对不同样品更具有灵活性.而同一元线性回归法相比,新方法能够更好地解决杂信号问题,得到的谱图更加干净易分辨.从图 2和图 3也可以看出,新方法比一元线性回归法稳定性更高,更可靠.通过比较可以发现,新方法优于前两种方法,能够很好地获得纯净的CHn子谱,用户使用此方法可以减少花在判断信号峰的时间,提高谱图分析的准确性和效率.
4 总结本文提出一种新的DEPT谱编辑方法,使用多元线性回归对样品数据进行处理.这种谱编辑新方法改善了现有DEPT谱编辑存在较多杂信号的不足,可以获得纯净的CHn子谱,对复杂和密集的碳谱线的解析和标识有重要意义.
| [1] | Doddrell D M, Pegg D T, Bendall M R . Distortionless enhancement of NMR signals by polarization transfer[J]. J Magn Reson , 1982, 48 (2) : 323-327 |
| [2] | Yuan Yun-fei(袁云飞), Hong Hai(洪海), Yang Xiao-yun(杨晓云) et al . The assignment of fluacrypyrim spectroscopy data(嘧螨酯波谱学数据全归属)[J]. Chinese J Magn Reson(波谱学杂志) , 2013, 30 (4) : 567-575 |
| [3] | Chen Zai-xin(陈再新), Yu Shui-tao(于水涛), Xia Zheng-jun(夏正君) . The organic spectral analysis of orlistat(奥利司他的有机波谱分析)[J]. Chinese J Magn Reson(波谱学杂志) , 2013, 30 (4) : 585-593 |
| [4] | Ding Ke-yang(丁克洋) . DEPT-(90+45), A new spectral editing technique DEPT-(90+45)(一个新的谱编辑技术)[J]. Chinese J Magn Reson(波谱学杂志) , 2000, 17 (1) : 79-82 |
| [5] | Ding Ke-yang(丁克洋) . An improvement to DEPT experiment(对DEPT实验技术的一点改进)[J]. Guangzhou Chemistry(广州化学) , 2000, 25 (1) : 39-42 |
| [6] | Rohr K S, Mao J . Efficient CH-group selection and identification in 13C solid-state NMR by dipolar DEPT and 1H chemical-shift filtering[J]. J Am Chem Soc , 2002, 124 (46) : 13 938-13 948 DOI:10.1021/ja027362m |
| [7] | Bendall M R, Pegg D T . Complete accurate editing of decoupled 13C spectra using DEPT and a quaternary-only sequence[J]. J Magn Reson , 1983, 53 (2) : 272-296 |
 2015, Vol. 32
2015, Vol. 32



