1. 华东师范大学 物理系，上海市磁共振重点实验室，上海 200062;
2. 上海卡勒幅磁共振技术有限公司，上海 201614
收稿日期: 2014-05-05
; 收修改稿日期: 2015-01-09
基金项目: 上海市科委资助项目(08DZ1900700)
作者简介:
李智敏(1987-)，女，山西长治人，硕士研究生，无线电物理专业
Spike Noise Removal for Magnetic Resonance Imaging Based on Sparse Reconstruction
1. Shanghai key Laboratory of Magnetic Resonance, Department of Physics, East China Normal University, Shanghai 200062, China;
2. Shanghai COLORFUL Magnetic Resonance Technology Corporation Limited, Shanghai 201614, China
引言
磁共振图像扫描中，受硬件故障、静电、磁场不均匀、机械振动等因素的影响，可能会在采集的原始数据（K空间）中产生幅值很大的异常点，即尖峰噪声点[1].尖峰噪声导致重建出的图像产生条纹状伪影，严重影响图像质量[2].如果重新对图像进行扫描，则会增加扫描时间.利用图像后处理算法来修复尖峰噪声点则能够节省额外的扫描时间，且有助于提高设备的使用率和图像的质量.
尖峰噪声修复的第一步是定位尖峰噪声，已有的定位方法有阈值法和背景信息法.阈值法利用MRI图像K空间数据的能量主要集中在低频区域的特点，设置动态阈值来判断尖峰噪声点的大小和位置[3]；背景信息法利用磁共振图像背景数据主要来自尖峰噪声和随机噪声的特点，选择背景区域的数据进行傅立叶变换得到对应的K空间数据，并对此数据进行分析从而获得尖峰噪声点的位置[4, 5].在找到尖峰噪声的位置之后，可以用插值1法进行修复[5]，即根据尖峰噪声周围的信号值估算出噪声位置的信号值.
压缩感知(Compressed Sensing，CS)技术是一种可以减少信号采样，降低信号存储、处理和传输成本的新型技术[6-9].该技术的理论是：如果信号在某个变换域上是稀疏的[10, 11]，可以用一个与变换基不相关的观测矩阵将高维信号投影到一个低维空间上[12]，然后通过求解优化问题就可以从这些少量投影中以高准确率重建出原信号[13-17].磁共振图像和普通自然图像相似，在小波变换后是稀疏的；而磁共振成像信号采集的K空间，是图像的傅立叶变换，和小波变换的相干性低，适合使用压缩感知技术.为进行磁共振图像的压缩感知重建，Lustig M等人采取了非线性共轭梯度(Nonlinear Conjugate Gradient，NCG)凸优化算法[17-19].如果在定位尖峰噪声之后，将尖峰噪声所在位置的数据看作是欠采的数据，就可以利用该算法对图像进行稀疏重建，达到修复尖峰噪声的效果.但由于该算法是在小波域实现的，在迭代过程中通过修改小波域数据进行能量函数的最小化，因此在重建过程中所有的K空间数据都将发生变化.而修复尖峰噪声仅需要改变尖峰噪声所遮盖的部分K空间数据即可，因此，为了达到最佳的保真效果，需要对该算法进行改进.针对这一问题，本文首先提出磁共振图像压缩感知的K空间重建算法，算法所用能量函数的自变量是K空间数据.在此基础上我们进一步提出可较好地修复尖峰噪声的K空间部分重建方法.该算法将尖峰噪声所遮盖区域添零，其他区域保持不变的K空间数据作为重建初始值，以重建图像在小波域和全变差域的稀疏性作为能量函数，使用非线性共轭梯度算法和回溯线搜索法迭代重建.与插值算法及传统的NCG方法相比，该算法可以更好地修复尖峰噪声.
1 基本理论
1.1 非线性共轭梯度凸优化的压缩感知重建算法
压缩感知算法处理的对象通常是在相位编码方向随机欠采样的K空间数据，随机欠采样时K空间中心区域采样概率要高于边缘区域，并且通常对中央最低频区域进行完全采样.对未采集的K空间部分用0填充后，进行反傅里叶变换和小波变换得到的小波域数据即可作为重建的初始值，接下来就可以进行图像重建，图像重建实际上是要解决如下的最优化问题：
|
$
\hat m = \arg {\min _m}||{F_u}{\Psi ^{ - 1}}m - {y_0}||_{{\kern 1pt} 2}^{{\kern 1pt} 2} + \alpha ||m||{{\kern 1pt} _1} + \beta {\kern 1pt} {\kern 1pt} {\rm{TV}}({\Psi ^{ - 1}}m)
$
|
(1) |
(1)式中右式的第一项是保真项，其中m是小波域数据，Ψ-1是反小波变换操作，Fu是傅里叶变换和欠采样操作，l2范数的定义为 $ ||x||{{\kern 1pt} _2} = {({\Sigma _i}|{x_i}|{{\kern 1pt} ^2})^{1/2}} $，y0则是采集到的K空间数据.保真项的作用是使得与重建图像对应的K空间数据中，与已经采集的K空间数据对应的行，接近原始采集的K空间数据.第二项是稀疏项，用于保证重建图像的小波变换是稀疏的，其中l1范数的定义为 $ ||x|{|_{{\kern 1pt} 1}} = {\Sigma _i}|{x_i}| $，而α是稀疏项的权重因子.第三项是图像的全变分(Total-Variation，TV)操作，用于保证图像的连续性，β则表示TV项的权重.
Lustig等人提出的非线性共轭梯度法，是一个用于解决上述最优化问题的迭代过程，每一次迭代i中均需求得下一步搜索所用的共轭方向矢量Δmi+1，并沿着该方向用回溯线性搜索法确定最优步长ti+1[17, 19].为获得共轭方向矢量Δmi+1，首先需要计算能量函数的梯度方向矢量gi：
|
$
{g_i} = \nabla ||{F_u}{\Psi ^{ - 1}}{m_i} - {y_0}||_{{\kern 1pt} 2}^{{\kern 1pt} 2} + \alpha {\kern 1pt} \nabla ||{m_i}|{|_{{\kern 1pt} 1}} + \beta {\kern 1pt} \nabla {\rm{TV}}({\Psi ^{ - 1}}{m_i})
$
|
(2) |
由于l1范数在0点处不连续，所以将l1范数近似表示为： $ ||x|{|_{{\kern 1pt} 1}} = {\Sigma _i}|{x_i}| = {\Sigma _i}\sqrt {x_i^2 + \mu } $，μ称为连续因子，取值为e-15，则l1范数的导数为 $ \frac{{{\rm{d}}||x||{{\kern 1pt} _1}}}{x} = {\Sigma _i}\frac{{{\rm{d}}|{x_i}|}}{x} = {\Sigma _i}\frac{{{x_i}}}{{\sqrt {x_i^2 + \mu } }} $.差分变换表示图像相邻行方向（或列方向）灰度的差异，图像像素的表示形式是复数，且为了避免分母为0，将差分变换结果表示近似为 $ \sqrt {x{x^*} + \mu } $，对其求导运算与l1范数的求导过程相同.求得梯度方向矢量gi后，重建共轭方向矢量Δmi+1为：
|
$
\Delta {m_{i + 1}} = \left\{ \begin{array}{l}
- {g_i},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}i = 0\\
- {g_i} + \frac{{||{g_i}||_{{\kern 1pt} 2}^{{\kern 1pt} 2}}}{{||{g_{i - 1}}||{\kern 1pt} _2^2}} \cdot \Delta {m_i},{\rm{ }}i \ne 0
\end{array} \right.
$
|
(3) |
(3)式中gi-1是上一次迭代的梯度方向矢量，Δmi是当前迭代的方向矢量.得到第i+1次迭代的共轭方向矢量Δmi+1后，根据回溯线性搜索法确定最优步长ti+1，即可求得第i+1次迭代的小波系数：
|
$
{m_{i + 1}} = {m_i} + {t_{i + 1}}\Delta {m_{i + 1}}
$
|
(4) |
重复上述迭代过程，直到迭代次数大于预先设定的最大迭代次数或者共轭方向矢量Δmi+1的l2范数小于预先设定的一个较小的阈值，则重建结束.迭代最后获得的小波系数经过反小波变换即可得到重建图像.
由于傅里叶变换和小波变换是线性变换，所以我们可以将上述NCG迭代优化过程进行改造，直接对K空间数据进行迭代，即本文提出的压缩感知K空间重建算法.
1.2 压缩感知K空间重建算法
与Lustig等人提出NCG算法不同的是：K空间重建算法直接对K空间数据以欠采样后添零的K空间数据y进行迭代优化，重建过程对如下能量函数进行优化：
|
$
f(y) = ||uy - {y_0}||{\kern 1pt} _2^2 + \alpha ||\Psi {{\rm{F}}^{ - 1}}y|{|_{{\kern 1pt} 1}} + \beta {\kern 1pt} {\kern 1pt} {\rm{TV}}({{\rm{F}}^{ - 1}}y)
$
|
上式中右式三项的意义与符号(1)式相同，第一项是保真项，其中y是迭代所得的K空间数据，u是欠采样操作，从重建数据中抽取与实际采样获得K空间数据对应的数据.第二项是稀疏项，其中F-1是反傅里叶变换操作，Ψ是小波变换操作.
每一次迭代中，首先求得共轭方向矢量Δyi+1：
|
$
\Delta {y_{i + 1}} = \left\{ \begin{array}{l}
- {g_i},{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}i = 0\\
- {g_i} + \frac{{||{g_i}||{\kern 1pt} _2^2}}{{||{g_{i - 1}}||{\kern 1pt} _2^2}} \cdot \Delta {y_i},{\rm{ }}i \ne 0
\end{array} \right.
$
|
其中gi是梯度方向矢量：
|
$
{g_i} = \nabla ||u{y_i} - {y_0}||{\kern 1pt} _2^2 + \alpha {\kern 1pt} \nabla ||\Psi {{\rm{F}}^{ - 1}}{y_i}||{{\kern 1pt} _1} + \beta {\kern 1pt} \nabla {\rm{TV}}({{\rm{F}}^{ - 1}}{y_i})
$
|
求得共轭方向Δyi+1后，利用回溯线性搜索法确定最优步长ti+1，即可获得第i+1次迭代的K空间数据yi+1为：
|
$
{y_{i + 1}} = {y_i} + {t_{i + 1}}\Delta {y_{i + 1}}
$
|
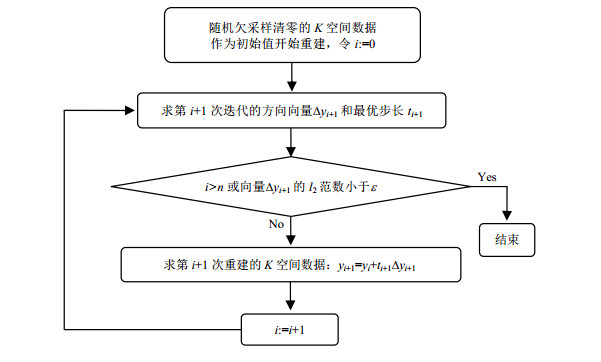
重复上述迭代过程，直到迭代次数大于预设的最大迭代次数或者共轭方向矢量Δyi+1的l2范数小于预先设定的一个较小的阈值，则重建结束.重建结果yi反傅里叶变换后即得到重建图像，算法流程图见图 1.
由傅里叶变换和小波变换的线性性质可知K空间迭代与小波域迭代是等价的，但K空间重建算法的好处是可以很容易修改算法，使其迭代过程中只对K空间部分数据进行迭代，实现K空间数据的完全保真.例如对于K空间数据中存在尖峰噪声的情况，只需要对尖峰噪声覆盖区域的K空间数据进行选择性地重建，就可以达到消除尖峰噪声的效果.
1.3 K空间部分重建算法
用于尖峰噪声消除的部分K空间重建算法不对已经采集的K空间数据进行修改，相应的能量函数与搜索的共轭方向都有所变化，由于迭代过程中不改变已经实际采样的K空间数据，这部分数据实现了完全保真，所以能量函数中就不再需要保真项：
|
$
f(y) = \alpha ||\Psi {{\rm{F}}^{ - 1}}y||{{\kern 1pt} _1} + {\rm{TV}}({{\rm{F}}^{ - 1}}y)
$
|
同样，迭代所用的梯度方向矢量gi变为：
|
$
{g_i} = \bar u[\alpha \nabla ||\Psi {{\rm{F}}^{ - 1}}{y_i}||{{\kern 1pt} _1} + \nabla {\rm{TV}}({{\rm{F}}^{ - 1}}{y_i})]
$
|
u类似前面的欠采样操作，作用是将与已采集的K空间数据对应部分的数据置为0，其余部分数据保持不变.利用这样的梯度矢量进行迭代，就可以保证迭代过程不会改变已经采集的K空间数据.
算法的迭代过程与K空间重建算法相同.算法在修复尖峰噪声时，先使用背景信息法[4, 5]找到尖峰噪声所在位置，把K空间中尖峰噪声所在位置的数据添零，其他数据点保持不变的值作为初始值，然后使用该算法进行迭代重建即可.
2 实验条件与结果分析
2.1 实验条件
本文所用大脑实验数据是在上海卡勒幅磁共振技术有限公司Sapphire 1.5 T超导磁共振成像系统采集的.扫描线圈为4通道头部线圈，扫描序列为自旋回波序列，扫描参数为：观察野(FOV)=240×240 mm，层厚(slice thickness)=1 mm，层数(slices)=16，回波时间(TE)=13 ms，重复时间(TR)=400 ms，采样矩阵(matrix)=256×256，原始四通道K空间数据中模值最大为21.80.图像水平方向为频率编码方向，竖直方向为相位编码方向.本文使用4级小波变换，基为db2，稀疏项权重α=2.5.
NCG算法的重建参数是：稀疏项权重α=0.005，全变分项权重β=0.002，使用4级小波变换，基为db2.
2.2 结果分析
为了对算法的效果进行评价，我们将本文算法与插值算法[5]进行了比较，此外，我们还利用Lustig提出的NCG方法对图像进行稀疏重建，评价了K空间部分重建对于尖峰噪声修复这类问题的优势.
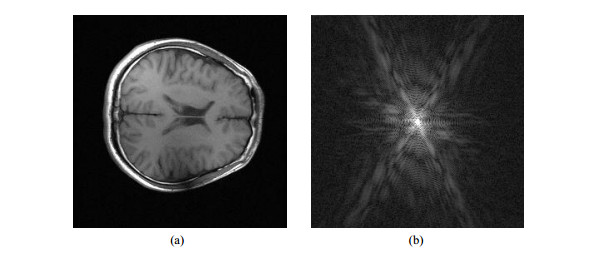
首先，我们利用前述数据进行了尖峰噪声修复的仿真实验.仿真实验选择第8层第1通道的数据，如图 2所示.首先在K空间中的随机位置添加15个幅值为50的连续尖峰噪声点（由于不同的修复算法对尖峰噪声覆盖区域都采取用覆盖的方法进行修复，所添加的尖峰噪声的幅值只影响尖峰噪声的定位，不影响尖峰噪声的修复效果），然后用不同方法对同样定位的尖峰噪声进行修复.计算修复后的图像与未添加尖峰噪声的图像的均方误差(Mean Square Error，MSE)作为评价算法优劣的定量标准.MSE的定义如下：
|
$
MSE = \frac{1}{{m \times n}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{[f(i,j) - f'(i,j)]}^2}} }
$
|
其中设图像大小为m×n，f(i, j)与f'(i, j)分别为修复后的图像与未添加尖峰噪声的原始图像.同样的实验重复100次，每次在不同的位置添加尖峰噪声，获得的MSE的均值与方差列于表 1.
表 1 不同算法MSE的均值和方差
Table 1 The mean and variance of MSE of different recoverying methods
|
| 本文算法 |
插值算法 |
NCG算法 |
| 均值 |
0.002 |
0.037 |
123.292 |
| 方差 |
0.002 |
0.095 |
12.407 |
从表 1可以看出，本文算法获得MSE的均值与方差都远远小于传统的插值算法，说明算法的修复尖峰噪声的效果好并且具有鲁棒性.而标准的压缩感知算法，由于会改变全部K空间的数据，所以对MSE有较大的影响，并不完全适用与尖峰噪声这类对K空间数据保真要求较高的场合.
由于磁共振成像的信号集中在K空间中央的低频区域，低频区域的尖峰噪声的修复也是尖峰噪声修复中最困难的.所以我们对K空间中央尖峰噪声的修复效果进行了评价.
如图 3(a)所示，我们在第127行的第1列~128列上添加尖峰噪声，然后用不同的修复方法进行修复.在不进行尖峰噪声消除的情况下，直接进行傅立叶变换，所得的图像完全被条纹状伪影污染[图 3(b)].而通过比较修复的结果，以及修复图[图 3(c), (e), (g)]与无尖峰噪声的图的残差图[图 3(d), (f), (h)]比较不难看出，本文提出的算法的效果明显优于其他的算法，在最低频半行数据污染的情况下，可以进行几乎完美的图像还原.
我们利用同一数据还进行了低频区尖峰噪声的修复效果的定量分析，在相位编码的第127行中心位置开始，对称地连续向两侧添加尖峰噪声，使用本文算法和插值算法进行图像还原，并记录最终结果与不带噪声图像之间的MSE.MSE随添加的尖峰噪声点数变化的情况如图 4所示.从图 4(a)中绘制了尖峰噪声点数小于256的情况（即在一行上），可以看出，由于K空间中一行的两侧的数据点比较小，因此插值算法在尖峰噪声点数增加到一定数量后，MSE就不再明显增加；而本文算法的MSE虽然随着尖峰噪声点数的增加而增加，但当整行全部为尖峰噪声时，取得的图像还原效果仍然优于插值算法对两个尖峰噪声点的还原效果.而当尖峰噪声点数超过256，或覆盖范围大于一行时，插值算法则迅速失效，从图 4(b)中可得本文算法仍然可以稳定地还原图像.因此可以说，使用本文提出的算法进行尖峰噪声消除，放宽了对尖峰噪声定位准确性的要求，即使在无法判断尖峰噪声准确位置时，适当放宽尖峰噪声的范围，本文算法仍然可以很好地还原图像.
3 结论
本文提出了利用稀疏重建消除尖峰噪声的方法，提出的K空间部分重建算法在消除尖峰噪声的同时，最大限度地实现了图像数据的保真，该算法在统计与视觉上均取得了良好的效果.由于K空间中央低频区域的尖峰噪声较难检测，同时影响到采集信号中能量最大的部分，因此也较难修复.而本文算法不仅能够很好地处理最低频区域的尖峰噪声，并且在进行图像还原时也放宽了对尖峰噪声定位准确性的要求，克服了之前算法因尖峰噪声定位不准确带来的无法准确还原图像的问题，因此无论尖峰噪声如何分布，本文算法均可较好地修复尖峰噪声.
2015, Vol. 32
表1(Table 1)
