文章信息
- 陈涛, 孙兵锋, 阎世栋, 梅刚华, 钟达
- CHEN Tao, SUN Bing-feng, YAN Shi-dong, MEI Gang-hua, ZHONG Da
- 一种小型化铷原子钟锁相倍频窄带VCO设计
- Design of a Narrow-Band Voltage Controlled Oscillator for Phase-Locked Frequency Multiplier in Miniature Rubidium Atomic Clock
- 波谱学杂志, 2014, 31(4): 587-595
- Chinese Journal of Magnetic Resonance, 2014, 31(4): 587-595
-
文章历史
收稿日期: 2014-03-17
收修改稿日期: 2014-10-29


2. 中国科学院大学,北京 100049;
3. 武汉工商学院 公共基础部,湖北 武汉 430065
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Basic Department, Wuhan Technology and Business University, Wuhan 430065, China
窄带VCO作为铷原子钟锁相倍频器的重要组成部分,其各项指标的好坏直接决定了倍频器输出射频信号的质量,如相位噪声、压控调谐范围和频谱纯度等这些因素.由于小型化铷钟电子学系统噪声水平与锁相倍频器输出信号质量密切相关.所以,我们的设计工作主要是围绕锁相倍频器VCO的压控特性、相位噪声、谐波抑制度、输出功率等这几个方面进行.本文将介绍这种窄带VCO的主要设计思路和测试结果.
1 压控振荡器(VCO)基本原理 1.1 振荡电路的结构我们通常设计的振荡电路一般是输出单一频率正弦波信号的振荡电路,主要结构为放大电路、反馈网络、选频网络和稳幅环节这些部分.放大电路是将直流电源能量转换为振荡输出交流能量,满足信号输出功率的要求.反馈网络与放大电路一起构成正反馈系统,以满足起振条件和相位平衡条件.选频网络是用来产生用户所需求的单一频率信号.稳幅环节是保证振荡输出信号的持续稳定,信号的波形不失真.
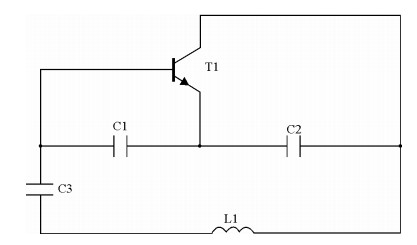
高频振荡电路放大元件通常是选用分立式晶体管,选频网络选用的是LC谐振回路.晶体管与LC谐振电路存在各种耦合方式,在高频中最典型的LC耦合振荡有哈特莱(Hartley)振荡,考毕兹(Colpitts)振荡[1].哈特莱振荡满足电感三点式振荡条件,该振荡电路容易起振,反馈信号是取自电感两端,输出波形中含有高次谐波,波形较差.考毕兹振荡满足电容三点式振荡条件,振荡同样容易起振,反馈信号是取自电容两端,输出波形较好,而且振荡频率可达几百MHz,但是频率调节不方便.为了提高频率稳定性,方便振荡频率调节,出现了多种改进型电容三点式振荡电路,克拉泼(Clapp)振荡电路就是其中一种,其交流等效电路参见图 1.
|
| 图 1 克拉泼振荡电路交流等效图 Fig. 1 Alternating current equivalent of clapp oscillator circuit |
克拉泼振荡是在考毕兹振荡电感支路L1中串联一小电容C3而构成,选取电容值C1 > > C3,C2 > > C3,通过调整C1和C2的比值,可使该振荡满足起振条件,而振荡频率是由L1和C3来决定[2].在本文的窄带VCO设计中,我们最终选取了振荡频率稳定、输出波形较好、频率调节方便的克拉泼振荡电路.
1.2 压控振荡器的特性参数对压控振荡器VCO来说,评估其特性的指标主要有振荡频率受控范围、压控特性、相位噪声、谐波抑制度、输出功率等参数.
振荡频率受控范围是指VCO的调谐带宽.VCO的调谐带宽与相位噪声是互相矛盾的.调谐带宽越宽, 通常其有载Q值越低,相位噪声越差.由于我们设计的是窄带VCO,即频率调谐带宽较小,因此输出信号的相位噪声较低.
调谐灵敏度即压控灵敏度Kd,是指控制电压的单位变化量ΔUc所引起的振荡频率的变化Δf,Kd=Δf/ΔUc.通常采用(1)式来近似描述
| $ {K_d} = \frac{{2\pi \left( {{f_{\max }}-{f_{\min }}} \right)}}{{{U_{c\max }}-{U_{c\min }}}} $ | (1) |
相位噪声指标是锁相环倍频系统的一个重要指标,而VCO作为锁相环倍频系统的一个重要部分,VCO的噪声大小也会直接关系到铷原子钟的稳定性.尤其要注意其VCO的低相噪设计,包括选取截止频率高,低噪声晶体管以及合适的晶体管静态工作点等.在铷原子钟倍频系统中我们最关注的是两倍调制频率处的相位噪声.该处的相噪高低也是反映VCO设计成功与否的关键.谐波抑制度是指VCO输出信号对各项高次谐波的抑制能力.通常我们关注VCO的二次谐波抑制度.
输出功率也是VCO的一项重要考核指标.所设计的VCO输出功率大小取决于电源电压、谐振网络的电容反馈比(对LC谐振电路来说),静态工作点等.在实际调试中,需要对这几个参数进行综合调整优化,得到需要的输出功率.
2 VCO电路仿真分析图 2是根据克拉泼振荡电路设计出的VCO电路工作原理图,我们根据该图对信号输出功率、谐波抑制度、压控特性进行了仿真分析和计算.

|
| 图 2 VCO仿真电路原理图 Fig. 2 Schematic diagram of VCO simulated circuit |
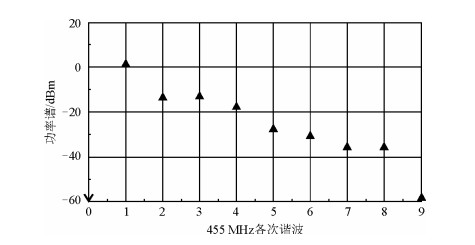
图 3是VCO输出信号各次谐波仿真分析结果,从仿真结果可以看出该VCO的输出信号功率为2~3 dBm,二次谐波抑制度约为-15 dBc,这与普通商用VCO的指标相当.
|
| 图 3 VCO仿真各次谐波功率谱 Fig. 3 VCO simulated harmixdex spectrum |
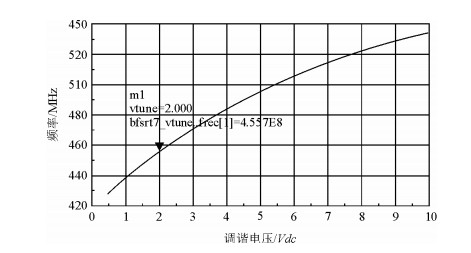
图 4为仿真得到的VCO压控频率特性曲线.从图中可以看出,该VCO的压控线性度较好,采用(1)式来计算该VCO的压控斜率约为18 MHz/V.当压控电压为2 V时,VCO的输出频率约为455 MHz.
|
| 图 4 VCO压控特性仿真曲线 Fig. 4 VCO voltage control characteristic simulated curve |
由窄带压控振荡器(VCO)电路设计原理可知,关键组成元件是晶体三极管、变容二极管和高Q值线绕电感.选取这3个元器件必须考虑的因素有输出频率覆盖范围、供电电压、输出信号相位噪声和谐振电路的品质因子等相关因素.
根据我们的小型化铷钟锁相倍频电路的设计方案,压控振荡器输出频率覆盖范围为440 MHz~470 MHz左右.首先是晶体三极管的选取,选用的晶体管特征频率要远大于其工作频率(约455 MHz).在噪声性能方面,双极晶体管振荡器更为优越,因此在我们的设计中,选取双极型晶体管.综合以上因素,并考虑到晶体管的封装、体积和功耗,我们最终选取Philip半导体公司生产的BFS17晶体管,其特征频率约为1 GHz.
变容管的选取直接影响着压控振荡器的频率覆盖范围.变容管的选取也要考虑其工作频段以及电容变化范围.考虑到压控振荡器的振荡频率如(2)式所示:
| $ f = \frac{1}{{2\pi \sqrt {L({C_0} + {C_j})} }} $ | (2) |
(2)式中,Cj为变容管电容,C0为谐振回路中其它电容的等效值.
若想通过改变变容管的Cj值来实现振荡频率从440 MHz~470 MHz的改变,则需
此外,对振荡频率起决定作用的电感L选用空心线圈制作,因为这样做出的电感Q值高,电路相对容易起振.
在设计VCO时,晶体管放大电路与谐振电路可能会深度耦合,结果会降低谐振电路的有效Q值,导致电路难以起振,它们之间应接入一个几pF的电容可以避免该现象[4].另外,谐振电感采用2~3匝的空心线圈,相对其它类型的电感(如瓷片表贴类的电感)空心线圈Q值要高些.最后,在设计时电路的寄生电容与配线寄生电感不能忽略,否则实际振荡频率和所需频率相差较大.根据ADS软件的仿真结果,将所设计的VCO电路经制板、元件安装后制成了电路实物,其照片如图 5所示,该VCO电路的体积约4 mL,适合于小型化铷原子钟的应用.

|
| 图 5 VCO实物图片 Fig. 5 VCO real object picture |
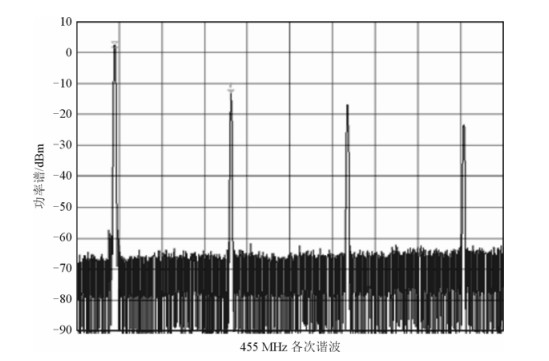
我们对设计制作出的VCO电路进行了实验调试和优化,并对VCO的输出信号功率谱进行了测试,测试结果如图 6所示.我们将频谱仪的SPAN设置为2 GHz来测试VCO输出信号和各次谐波的功率,从图 6中可以看出,该VCO输出信号功率约为2 dBm,二次谐波抑制度达到-15.5 dBc,这与本文图 3中所示的仿真结果吻合度较好.
|
| 图 6 VCO实测功率谱 Fig. 6 VCO power spectrum |
我们将研制出的VCO进行了压控特性的测试.具体办法是,VCO的供电电压为5 V,将压控端接至可调电压源的输出端,按0.5 V步进从0 V~4.5 V扫描压控电压,并依次测试VCO各工作点的频率,得到的压控频率特性曲线如图 7所示.
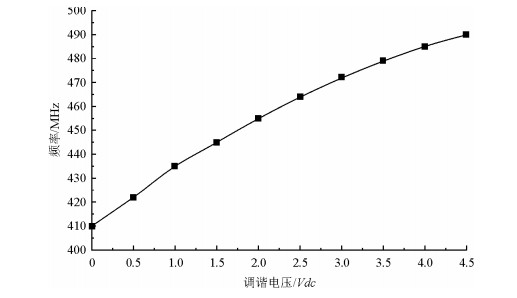
|
| 图 7 VCO压控特性实测曲线 Fig. 7 VCO voltage control-characteristic measured curve |
从图 7实测的压控特性曲线可知,该VCO的压控灵敏度为17.7 MHz/V,与本文图 4仿真的结果18 MHz/V基本一致.当压控调谐电压为2 V左右时,VCO输出频率约为455 MHz,正是我们铷钟锁相倍频器所需的工作频率.
4.3 相位噪声测试为了对本文设计的VCO电路的性能作进一步的测试和评估,我们将该VCO电路模块接入到小型化铷钟锁相倍频电路中,锁相倍频器的输出信号为受调制的455 MHz射频信号.我们用PN9000相位噪声系统测试了该455 MHz信号的相位噪声特性,如图 8所示.

|
| 图 8 相位噪声测试结果 Fig. 8 The measured result for phase noise |
该455 MHz信号经匹配和SRD阶跃倍频后将输入到铷钟量子系统,根据铷钟工作机理,其在2倍调制频率(2fm)处的相位噪声与铷原子钟稳定度指标直接相关.由于我们设定的调制信号频率fm为136 Hz,那么2fm即为272 Hz.从图 7测试结果可知,窄带VCO构成的锁相环在2fm处的相位噪声为-94 dBc/Hz,根据铷原子钟频率稳定度与2fm相位噪声的关系式[5-7],可推算出该电路相位噪声对铷钟频率稳定度指标的贡献约为5×10-12τ-1/2.
5 结束语我们设计了一款用于小型化铷原子钟锁相倍频器的窄带VCO电路,该电路采用了稳定性高、输出波形较好、频率调节方便的克拉泼电路方案.应用ADS2008高频仿真软件对所设计的VCO电路进行了仿真,对VCO电路的信号功率谱、谐波抑制度以及压控特性等进行了仿真分析.最终在硬件上设计并实现了这种窄带VCO电路,其输出频率范围为440 MHz~470 MHz,频率调谐灵敏度为18 MHz/V,二次谐波抑制度为-15 dBc,由该VCO电路构成的铷钟锁相倍频器具有良好的相位噪声特性,对小型化铷原子钟系统的频率稳定度的贡献达到5×10-12τ-1/2的水平.
| [1] | Chikawa Yuichi (Japan)(市川裕一), Zhuo Sheng-peng(卓胜鹏) . Design and Manufacture of High Frequency Circuit(高频电路设计与制作)[M]. Beijing(北京): Science Press(科学出版社), 2006 . |
| [2] | Li Shu-fang(鬲淑芳) . The Analog Electronic Technology(模拟电子技术基础)[M]. Shanxi(陕西): Shanxi Normal University press, Third Edition(陕西师范大学出版社), 2005 . |
| [3] | Zhong Heng(钟恒), Si Lei(司雷), Wang Yong(王勇) . A novel wideband VCO design(一种新型的宽带压控振荡器的设计)[J]. Instrumentation(仪器仪表用户) , 2006, 16 (2) : 112-115 |
| [4] | Audoin C, Candelier V, Dimarcq N . A Limit to the frequency stability of passive frequency standards due to an intermodulation effect[J]. IEEE T Instrum Meas , 1991, 40 (2) : 121-125 DOI:10.1109/TIM.1990.1032896 |
| [5] | Deng J Q, De Marchi A, Walls F L, et al. Frequency stability of cell-based passive frequency standards: reducing the effects of local-oscillator PM noise[C]//IEEE Frequency Control Symposium, 1998. Proceedings of the 1998 IEEE. International. Pasadena, CA: 1998, 95-98. |
| [6] | Mileti G, Deng J Q, Walls F L, et al. Recent progress in laser-pumped rubidium gas cell frequency standards[C]//IEEE Frequency Control Symposium, 1996. Proceedings of the 1996 IEEE International. Honolulu, HI: 1996, 1 066-1 072. |
| [7] | Wang Yi-qiu(王义遒), Wang Qing-ji(王庆吉), Fu Ji-shi(傅济时) et al . Theory of Quantum Frequency Standard(量子频标原理)[M]. Beijing(北京): Science Press(科学出版社), 1986 : 200 -202. |
| [8] | Liu Jing(刘静), Sun Bing-feng(孙兵锋), Yan Shi-dong(阎世栋) et al . A method for microwave frequency multiplication in miniaturized rubidium atomic clocks(一种微波倍频方案在小型化铷钟的应用)[J]. Chinese J Magn Reson(波谱学杂志) , 2013, 30 (4) : 559-565 |
 2014, Vol. 31
2014, Vol. 31



