文章信息
- 钟彩娇, 陈志伟, 陈忠
- ZHONG Cai-jiao, CHEN Zhi-wei, CHEN Zhong
- 核磁共振谱自动基线校正新方法
- An Automatic Baseline Correction Method for NMR Spectra
- 波谱学杂志, 2014, 31(4): 523-534
- Chinese Journal of Magnetic Resonance, 2014, 31(4): 523-534
-
文章历史
收稿日期: 2014-03-01
收修改稿日期: 2014-10-29


在核磁共振(Nuclear Magnetic Resonance, NMR)研究中,谱图基线失真的原因有很多,往往来源于硬件、处理过程或其他复杂原因[1, 2],包括仪器不稳定性、滤波器相位非线性响应和FID数据前几个点的损坏等[2, 3].基线失真会直接影响NMR谱的定量分析以及谱峰分配的准确性和精确度[4-6].为了获得平坦的基线,现代谱仪一般采用过采样和数字信号处理,但仍无法处理所有的基线失真[7, 8].同时,随着对二维谱和多维谱研究的深入,人工基线校正方法将十分费时且不易达到最佳效果,自动基线校正方法显然更有效率及实用性.
自动基线校正方法可以笼统地分为含参数方法和无参数方法.目前,一些常用的含参数方法很多都是基于Whittaker滤波器实现的[9].该滤波器的使用大大提高了基线校正算法的速度和灵活性,并且在MATLAB编程中其基础算法仅用几行代码就能实现. 2006年,Cobas等人提出的全自动基线校正方法[10],使用连续小波变换结合Whittaker滤波器,解决了低信噪比谱的基线校正难题,然而该方法无法很好地识别宽峰;2012年,鲍庆嘉等人在该基础上提出了一种基于迭代的自动基线校正方法[11],其自动基线识别方法(Baseline Recognition with Combination and Improvement, BRCI)结合3种算法的优点,能良好地识别包括宽峰在内的所有谱峰,在基线建模过程采用基于Whittaker滤波器的迭代方法,并引入“准基线点”消除负区域,但该算法在基线非线性失真时可能导致峰区域基线偏低.理论上,最佳的基线拟合方法应该不含参数或参数尽量少,然而实践中,无参数的基线校正方法一般比较难达到理想效果.大部分无参数方法基于多项式拟合,在低信噪比和基线复杂的情况下,多项式拟合方法无法拟合出最佳的基线模型[12].最近的研究中,自动迭代移动平均值方法(Automated Iterative Moving Average, AIMA)的基线校正效果比较理想[13],然而仍有不足之处,AIMA方法在峰区域容易将基线估计的过高[14],导致谱峰强度减小.
为了解决由基线非线性失真造成的校正错误,本文提出了一种自动迭代的基线校正新方法,在BRCI方法的基础上,结合了它和AIMA方法的优点并加以改进,改善了峰区域的基线建模效果.新方法适用于NMR谱的基线校正,并且在基线严重非线性失真的情况下也能建立比较理想的基线模型.
1 理论 1.1 自动基线识别新方法的基线识别结合了BRCI方法和AIMA方法的优点,增加了对峰区域的计算,能更充分地利用峰区域的数据点.
新方法首先利用BRCI方法识别出所有基线和峰信息:其中BRCI方法先使用连续小波变换,目的是得到导数谱并消除基线起伏[15],然后利用滑动窗口算法[16]识别基线点和信号点,最后利用改进的迭代阈值方法识别宽峰[17].这个过程将识别出的所有峰分成了多个区域,并且得到其位置信息,然后判断出峰的正负[11].峰的正负具体判断过程如下:把峰区域的首尾点的平均值作为峰偏离坐标轴的高度,整个峰区域减去这个值后再找出该峰区域的绝对值高度最高的位置,记该位置的峰值为Hmax,并将|Hmax*σ|作为阈值(σ为比例系数,文献中设为0.1,用户可根据需要适当调整该系数).若Hmax > 0,并且该区域包含的所有负值均不超过阈值,则标记该峰为正峰,否则不标记;若Hmax < 0,并且该区域包含的所有正值均不超过阈值,则标记该峰为负峰,否则也不做标记.对这些不做标记的峰区域进行线性插值以此作为该区域的基线,后续不做其他处理.
识别出峰信息后,为了更好地建立峰区域的基线模型,新方法找到峰区域内的“基线定位点”作为基线点参与后续的基线建模.“基线定位点”的确定主要结合AIMA方法中的迭代平均值算法(Iterative Averaging, IA)实现,并且仅对峰区域进行计算,以下以正峰为例:
第一步,使用AIMA算法中的迭代平均值步骤,拟合出该峰区域的基线,然后选取临时“基线定位点”,具体步骤如下:
记峰区域序列为y,长度为N,首次迭代更新偶数点如下:
| $ {y_{i + 1}} = \min [{y_{i + 1}},({y_i} + {y_{i + 2}})/2],\;i = 1,3,5 \cdots ,N - 3,N - 1 $ | (1) |
第二次迭代更新奇数点如下:
| $ {y_{i + 1}} = \min [{y_{i + 1}},({y_i} + {y_{i + 2}})/2],\;i = 2,4,6 \cdots ,N - 4,N - 2 $ | (2) |
紧接着,去掉首尾点,迭代更新偶数点:
| $ {y_{i + 1}} = \min [{y_{i + 1}},({y_i} + {y_{i + 2}})/2],\;i = 3,5 \cdots ,N - 5,N - 3 $ | (3) |
以此类推,再去掉一次首尾点,迭代更新奇数点:
| $ {y_{i + 1}} = \min [{y_{i + 1}},({y_i} + {y_{i + 2}})/2],\;i = 4,6 \cdots ,N - 6,N - 4 $ | (4) |
当第一个更新点i达到floor(N/2)时,迭代终止,此时峰区域得到一条未最大化谱峰的基线y.对负峰而言,应先将其取反,按上述步骤得到负峰区域的基线后,将得到的基线连同负峰再次取反,使该区域的基线回到原来负峰所在的位置上,以此作为初始信号序列的一部分.负峰区域基线的建立均可按这样两次取反的步骤得到,这样可以保证基线的连续性,以下不再赘述.
根据公式不难发现,基线y低于任何信号点,即在峰区域信号扣除迭代平均值步骤得到的基线不会产生任何负区域.利用这样的优点,新方法选取该基线y的所有局部极小值点,作为临时“基线定位点”.
第二步,新方法将所有临时“基线定位点”及峰的两个边界点进行顺序线性连接,得到一个临时序列y′,并去除“尖峰定位点”,得到满足条件的“基线定位点”.
所谓“尖峰定位点”,即序列y′中的局部极大值点,去除这些点的定位标记.这样做是防止加入裂峰处的局部极小值点,导致所得基线过高,并加快基线建模速度.同时,去掉这样的尖峰定位点并不会影响基线建模效果.
新方法将峰区域的“基线定位点”和非峰区域的基线点一起用于基线建模.同时,获取后续建模过程中将用到的基线ya=min(y, y′).
1.2 基线建模基线校正的关键步骤是建立基线模型,将原始谱减去基线模型得到没有基线失真的谱图.在以前的基线校正方法中,一般只采用基线识别所得的基线点来进行基线建模.BRCI方法虽然引入“准基线点”参与基线建模,但在无负区域出现的情况下,相当于仅对峰区域进行线性插值,在这种情况下要保证校正正确的前提是峰区域的基线线性失真;若在非线性失真情况下,仅依靠几个“准基线点”并不能很好地建立基线模型.例如,若在峰密集区域基线向上非线性弯曲,线性插值后并不会出现负区域,也即不引入任何“准基线点”,这样得到的基线模型在该区域就会偏低,导致该峰区域峰强度增大,造成校正错误.
新方法加入“基线定位点”参与基线建模,并利用迭代方法消除负区域.基线建模是基于Whittaker滤波器[9]原理实现的迭代方法.
设信号序列为等间隔的序列y,长度为N,计算得到的基线序列为z,滤波器的权向量序列为w,第m次迭代的目标函数为
| $ {Q_m} = \sum\limits_{i = 1}^N {{w_m}(i){{[{y_m}(i)-{z_m}(i)]}^2}} + \lambda \sum\limits_{i = 2}^{N - 1} {{{[\Delta {z_m}(i)]}^2}} $ | (5) |
(5)式中,权向量
(5)式中的第一项代表信号保真度,即所得的基线偏离原始数据的程度,用
首次迭代时,将基线识别过程得到的基线点和“基线定位点”的权值设为1,其余信号点的权值设为0,得到初始权向量w1.
初始信号序列y1由基线区域的数据点和峰区域的初始基线组成.峰区域的初始基线利用AIMA方法中的迭代平均值平滑(Iterative Averaging Smoothing, IAS)步骤得到:将自动基线识别过程(上文1.1小节)最后一步得到的基线ya,经IAS步骤处理后得到序列基线yb,则峰区域
首次迭代得到基线模型为z1.计算此次信号序列和基线模型的基线差值
第二次迭代,标记D1负区域中的局部极小值点为“基线定位点”(设该点权值为1),得到新的权向量序列w2.这个过程同时也消除了一些因谱峰识别错误而产生的负区域,这部分负区域中的“基线定位点”效果等同于BRCI方法的“准基线点”.
不改变基线数据点,令峰区域
新方法的算法流程图见图 1.
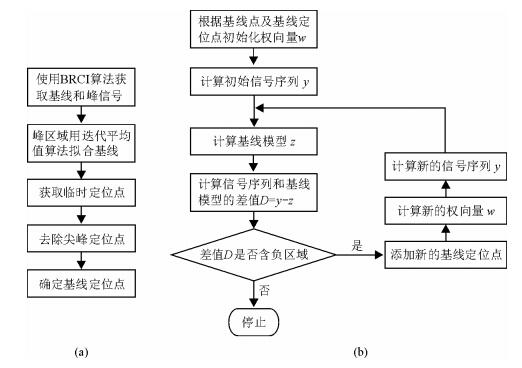
|
| 图 1 新方法的算法流程图. (a)基线识别流程图;(b)基线建模流程图 Fig. 1 Flow chart of new method. (a) Flow chart of baseline recognition, (b) flow chart of baseline modeling |
图 2为新方法对NMR谱的处理过程图.图 2(a)为经IA算法计算得到的基线(非峰区域保留了原数据点).找出峰区域的局部极小值线性连接得到图 2(b),去除“尖峰定位点”后得到图中“▲”表示的“基线定位点”.基于IAS算法计算得到图 2(c)所示的初始基线.图 2(d)展示了最终的基线模型.图 2(e)为基线校正后的结果.
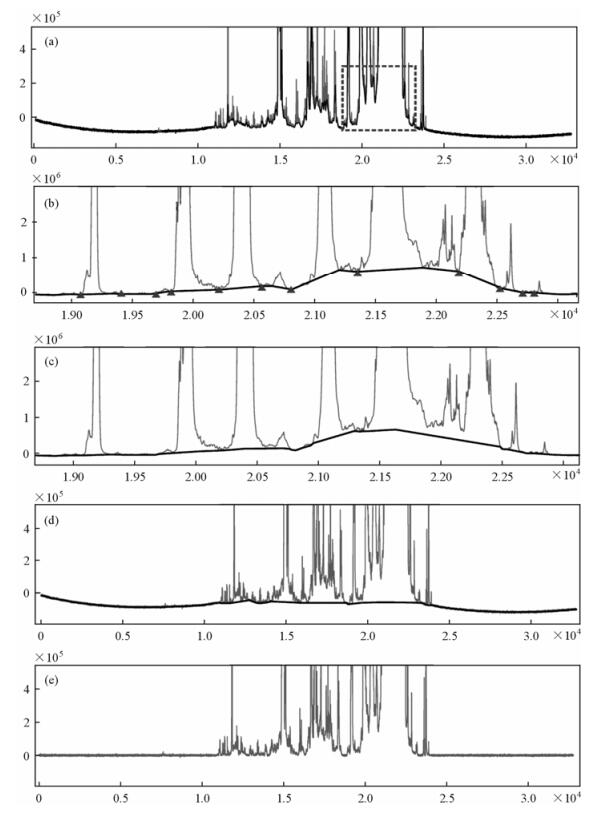
|
| 图 2 新方法改进部分的处理过程示意图,(a)原始NMR谱经迭代平均值计算后得到的基线,(b)顺次线性连接峰区域的所有局部极小值点,求出“基线定位点”[仅显示(a)中方框所示范围,“▲”代表基线定位点],(c)基于移动均值平滑算法得到的峰区域初始基线[仅显示(a)中方框所示范围],(d)迭代后得到的基线模型, (e)校正后的谱图 Fig. 2 An illustration for processing procedure of the new method, (a) baseline built by using Iterative Averaging on the original NMR spectrum, (b) linearly connect all local minimal points and find out 'baseline anchor points' [Only shows the region within the rectangle in (a), 'baseline anchor points' are denoted by '▲'], (c) an initial baseline built based on Iterative Averaging Smoothing [Only shows the region within the rectangle in (a)], (d) baseline model after iteration, (e) resulted spectrum after baseline corrected |
对一个由于时间域信号前几个数据点损坏导致基线较大程度非线性失真的一维谱图进行基线校正,图 3对比了AIMA方法、BRCI方法和新方法在该情况下的基线校正结果.图 3(a)和(b)两个纵列分别代表3种方法的基线建模结果和基线校正结果.从图 3可以看到,在右侧谱峰密集并且畸变较大的区域,3种方法得到的结果有很明显的区别.AIMA方法在谱峰密集区域所得的基线建模结果有很多凸起,基线估计略偏高,谱图校正后,该区域的峰强度减小;而在基线向上弯曲并且失真程度比较大的位置,基线失真可能被识别成宽峰,例如在图 3(b)中“※”号标注的区域基线估计得过低,校正后出现伪峰.BRCI方法在该区域没有使用任何数据点,基线为线性,导致该区域基线过低,校正后峰积分面积增大.新方法得到的基线建模结果良好,谱图校正后基线平整,峰积分面积比例保持良好.对图 3(b)校正后的谱图进行积分:选取“▲”号标注的两个甲基峰进行积分,则其理论比值应为1:1.经过计算,AIMA方法和新方法得到的比值分别为1:1.04和1:1.05,这两个结果比较相近,准确度较高;而BRCI方法校正后两个甲基峰的积分比值为1:1.24,结果偏差较大.
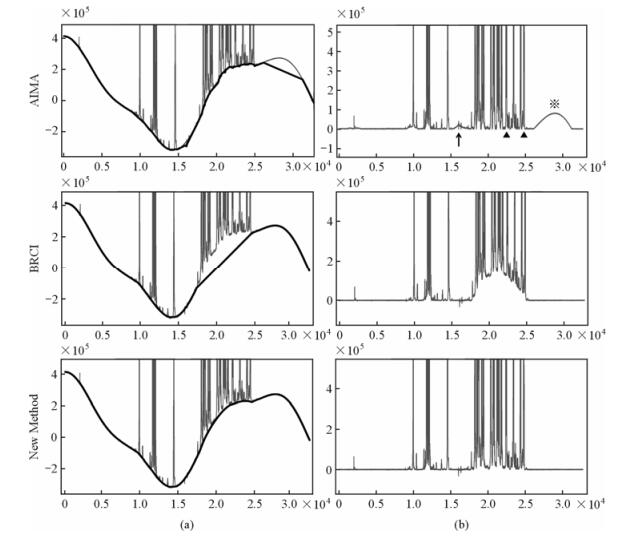
|
| 图 3 AIMA方法,BRCI方法(λ=200)和新方法(λ=200)分别对基线严重失真的NMR谱校正的结果,(a) 3种方法基线建模结果对比,(b) 3种方法谱图校正效果对比 Fig. 3 NMR spectra with serious baseline distortion respectively corrected by AIMA, BRCI(λ=200) and new method(λ=200). (a) Comparation of baselines built by the three different methods, (b) comparation of spectra corrected by the three different methods |
图 3(b)中箭头所指处的凸起是因为该处出现一个负信号,而AIMA方法拟合的基线会低于任何信号,因而无法得到正确结果.该方法必须结合其他谱峰识别方法,才能处理含负峰的谱图,否则就会出现错误校正.
通过对比可以发现,新方法结合了两种方法的优点并改进,所得结果既弥补了BRCI方法在峰区域的基线建模的不足,又不会出现AIMA方法那样基线估计不理想的情况,新方法即使在较大程度非线性失真的情况下也能得到比较理想的基线建模效果.
2.2 不同峰形的基线建模结果分别使用AIMA方法、BRCI方法和新方法对1D 1H NMR谱进行基线建模,得到图 4所示的3种不同方法的基线建模结果对比.

|
| 图 4 3种不同方法在不同情况下的基线建模结果对比,A,B,C区域分别代表低信噪比、谱峰密集和峰形良好3种情况(BRCI方法和新方法的平滑系数均设置为λ=600) Fig. 4 A comparation of baseline models built by the three different methods under different situations. A, B, C respectively represent three situations: low SNR, crowed peaks and well-behavior peaks. (The smoothing factors of BRCI method and new method are both set as λ=600) |
图 4中A,B和C三组图分别代表低信噪比、谱峰密集和峰形良好3种不同情况下的基线建模结果.
在低信噪比和峰形良好的情况下,新方法和BRCI方法的校正结果相近,均为线性,而AIMA方法在这两种情况下得到的基线比其他两种方法偏低.这可能是由于AIMA方法所得的基线低于任何噪声,而其他两种方法所得的基线在噪声的平均值位置;在谱峰密集的情况下,AIMA方法所得的基线偏高,BRCI方法得到的基线为直线,新方法得到的基线能较好地贴合峰底部,又不会导致基线偏高.
2.3 平滑系数对基线建模结果的影响由于存在谱峰重叠,对比图 4中B组的图,BRCI方法和新方法的建模结果哪一个更合理,我们暂时不做判断.但是经过数据验证,随着平滑系数λ的改变,BRCI方法在该区域的建模结果并不会改变(由于不出现负区域,在峰区域建模结果始终为直线),而新方法所得的基线贴合底部的程度却会变化,用户可以利用这个性质,选择合适的参数建立理想的基线模型.
使用不同的平滑系数,用新方法对图 4的谱再次进行基线建模,得到图 5的结果(图中显示的范围与图 4中B组的一样).图 5展示了不同的平滑系数λ对新方法基线建模结果的影响.从结果可以看到,随着平滑系数的增大,新方法所得基线逐渐偏离峰底部:当平滑系数λ过小时会导致基线过高(λ=400),而系数越大,新方法所得的基线结果越趋向线性插值.图中,当λ=3 200时所得的基线几乎为线性,与图 4中BRCI所建立的基线相近.

|
| 图 5 不同的平滑系数λ对新方法基线建模结果的影响 Fig. 5 The effects on baseline modeling by using new method with various smoothing factors λ |
因此,新方法具有较大的灵活性,可以根据基线失真的程度调节平滑系数λ,从而得到最合适的基线.根据经验,对于基线失真较严重的,一般使用较小的平滑系数能得到更理想的基线模型;反之,则使用较大的平滑系数.
2.4 对碳谱的基线校正除了对质子谱的基线校正,新方法同样适用于碳谱的校正.图 6展示了BRCI方法和新方法对碳谱的基线校正结果(由于AIMA方法无法处理负峰,此处不做对比).
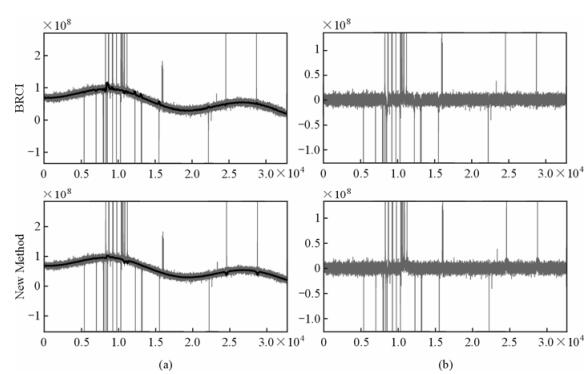
|
| 图 6 BRCI方法和新方法对1D 13C NMR谱的基线校正,(a)两种方法的基线建模结果(平滑系数均为λ=10 000),(b)两种方法基线校正后的谱图 Fig. 6 Baseline correction of 1D 13C NMR spectra by BRCI and new methods, (a) baseline models (b) resulted spectra after baseline corrected |
实验过程中,两种方法均保持相同的平滑系数,当平滑系数设置较大的值时能同时得到较好的基线结果,当λ=10 000时分别得到图 6(a)一组所示的基线模型.相比于噪声水平,两种方法在该参数下的基线建模结果相差较小,基线模型较理想.从图 6(b)可以看到,两种方法的校正结果基本相近,均能得到基线较佳的谱图.
设置不同的平滑系数,用BRCI方法和新方法分别对上面的数据进行处理,得到图 7所示的结果(图中仅显示局部碳谱).
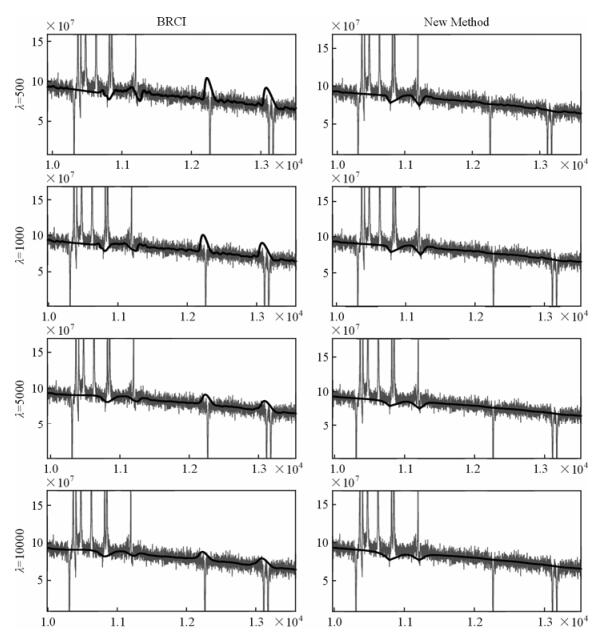
|
| 图 7 BRCI方法和新方法在不同平滑系数下对碳谱的基线建模结果对比 Fig. 7 A comparation of baselines built by BRCI method and new method with different smoothing factors |
对比第一列图可以发现,平滑系数越大,BRCI方法在峰区域得到的基线越理想.而当平滑系数太小时,BRCI方法在峰区域得到的基线偏离理想值,导致基线校正后峰强度增大.经分析,这可能是由于BRCI方法在峰区域所得的基线不靠或仅靠少数个“准基线点”建立,面对碳谱这样噪声较大的谱时容易受噪声影响,使得基线建模不理想.对比第二列图,新方法在变化范围较大的参数值下所得的基线建模结果都相近,除了基线的平滑度不同外基本区别不大.
通过上述的对比,不难发现在对碳谱的基线建模过程中,新方法对参数的依赖程度低,相比BRCI方法能节约更多的参数调试时间,并且不容易产生校正错误.
4 总结本文提出了一种新的NMR谱自动基线校正方法,它是在BRCI方法和AIMA方法的基础上进行有机的结合和改进.该方法最重要的改进在于解决了基线非线性失真情况下的基线建模问题,并且也适用于一般情况下的基线校正.对比传统方法对峰区域数据的忽视,新方法在峰区域引入“基线定位点”,能更大程度地利用峰区域的数据.实验结果表明新的自动基线校正方法对基线严重失真的NMR谱能获得比较理想的基线建模结果,从而对谱图进行更佳的基线校正.新方法采用MATLAB编程实现,其源程序可向作者索取.
| [1] | Hoch J C, Stern A S . NMR Data Processing[M]. New York: Wiley-Liss, 1996 . |
| [2] | Tang C G . An analysis of baseline distoration and offset in NMR spectra[J]. J Magn Reson , 1994, 109 (2) : 232-240 DOI:10.1006/jmra.1994.1160 |
| [3] | Marion D, Bax A . Baseline distoration in real fourier transform NMR spectra[J]. J Magn Reson , 1988, 79 (2) : 352-356 |
| [4] | Wang Chao(王超), Huang Ying-ying(黄颖颖), Yang Guang(杨光) . Automatic phase correction for NMR spectra -connecting line of equally spaced points(clesp)(核磁共振谱图自动相位校正新方法--等密度点连线法)[J]. Chinese J Magn Reson(波谱学杂志) , 2004, 21 (4) : 445-457 |
| [5] | Huang Ying-ying(黄颖颖), Li Peng(李鹏), Liu Xiao-zheng(刘小征) et al . A synthetical algorithm for automatic phase correction of NMR spectra based on neural network (NNAPC)(基于神经网络的NMR谱图自动相位校正综合算法)[J]. Chinese J Magn Reson(波谱学杂志) , 2007, 24 (1) : 43-51 |
| [6] | Yuan Qing-quan(袁清泉), Guo Jun-wang(郭俊旺), Cong Jian-bo(丛建波) et al . An EPR data acquisition and control system for in vivo tooth dosimetry(在体剂量检测专用EPR数据采集与控制系统)[J]. Chinese J Magn Reson(波谱学杂志) , 2013, 30 (3) : 354-360 |
| [7] | Moskau D . Application of real time digital filters in NMR spectroscopy[J]. Concept Magn Reson , 2002, 15 (2) : 164-176 DOI:10.1002/(ISSN)1099-0534 |
| [8] | Wider G . Elimination of baseline artifacts in NMR-spectra by oversampling[J]. J Magn Reson , 1990, 89 (2) : 406-409 |
| [9] | Eilers P H C . A perfect smoother[J]. Anal Chem , 2003, 75 (14) : 3631-3636 DOI:10.1021/ac034173t |
| [10] | Cobas J C, Bernstein M A, Martin-Pastor M et al . A new general-purpose fully automatic baseline-correction procedure for 1D and 2D NMR data[J]. J Magn Reson , 2006, 183 (1) : 145-151 DOI:10.1016/j.jmr.2006.07.013 |
| [11] | Bao Q J, Feng J W, Chen F et al . A new automatic baseline correction method based on iterative method[J]. J Magn Reson , 2012, 218 : 35-43 DOI:10.1016/j.jmr.2012.03.010 |
| [12] | Zhao J H, Lui H, McLean D I et al . Automated autofluorescence background subtraction algorithm for biomedical Raman spectroscopy[J]. Appl Spectrosc , 2007, 61 (11) : 1225-1232 DOI:10.1366/000370207782597003 |
| [13] | Prakash B D, Wei Y C . A fully automated iterative moving averaging (AIMA) technique for baseline correction[J]. Analyst , 2011, 136 (15) : 3130-3135 DOI:10.1039/c0an00778a |
| [14] | Johnsen L G, Skov T, Houlberg U et al . An automated method for baseline correction, peak finding and peak grouping in chromatographic data[J]. Analyst , 2013, 138 (12) : 3502-3511 DOI:10.1039/c3an36276k |
| [15] | Shao X G, Ma C X . A general approach to derivative calculation using wavelet transform[J]. Chemometr Intell Lab , 2003, 69 (1-2) : 157-165 DOI:10.1016/j.chemolab.2003.08.001 |
| [16] | Golotvin S, Williams A . Improved baseline recognition and modeling of FT NMR spectra[J]. J Magn Reson , 2000, 146 (1) : 122-125 DOI:10.1006/jmre.2000.2121 |
| [17] | Dietrich W, Rudel C H, Neumann M . Fast and precise automatic base-line correction of one-dimensional and 2-dimensional NMR-spectra[J]. J Magn Reson , 1991, 91 (1) : 1-11 |
 2014, Vol. 31
2014, Vol. 31



