Design and Construction of a Fully-Opened Unilateral Nuclear Magnetic Resonance System
引言
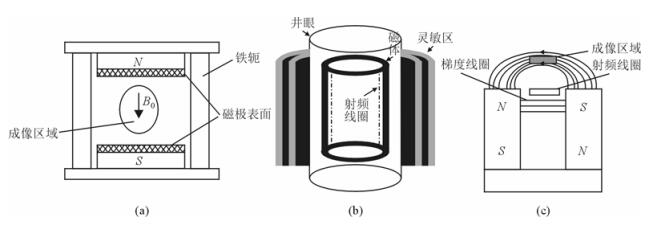
自1946年发现至今，核磁共振技术以其多参数检测、高对比度、无创等优点，在生物医学、材料化学、建筑、农业等领域得到了广泛应用[1-3].常规NMR仪器（包括波谱仪、成像仪和分析仪）依赖于高度均匀性的磁场，所以采用磁体包围样品(outside-inside)模式，在大磁体产生的高度均匀磁场中进行小样品的检测与成像，如图 1(a).其系统价格昂贵，半封闭结构还严重限制了核磁共振技术的应用与拓展[1-3].
非常规的核磁共振系统相比于常规核磁共振系统有很多的优越性，如开放性、低成本、便携性等，从而可使核磁共振分析技术广泛应用于食品品质检测、文化古迹勘察保护等领域.其全开放式特点可消除病人的幽闭恐惧症，使肥胖病人不再受到检查限制，还可开展介入治疗等.同时单边磁体产生的高达数T/m的自然恒定磁场梯度可用以测量扩散弛豫系数，可彻底避免常规核磁共振测量扩散系数需要施加大电流（用以产生脉冲梯度磁场）以及产生难以彻底消除的涡流效应[1-3].
非常规的核磁共振技术思想（Inside-Outside模式）于1978年由美国Los Alamos国家实验室的Jasper Jackson博士提出：在井眼中布置永磁体，在井眼外部的地层中构建背景主磁场，以满足核磁共振条件，并设计出第一台基于这种思想的核磁共振测井仪器，见图 1(b).
Jackson博士的这一项目在应用层面上意义非凡，即首先放宽了对NMR背景场的均匀性要求，其背景场场强矢量只要模值相同，方向可以不一致.同时他首次提出了工程上实现柱壳状磁场样品区的一种磁体构成方案——对极磁体方案.此类构型在石油领域持续的高额投入研发，逐步形成了成熟的核磁共振测井仪.目前有美国哈里伯顿公司的MRIL(MRI Logging)系列产品，美国斯伦贝谢公司推出的CMR系列产品以及俄罗斯生产的MK923系列产品等，价格都十分昂贵.受此启发，随后美国和欧洲的科学家对Jackson博士的“Inside-Out”思想进一步发展，提出基于单边磁体的新型核磁共振构型，图 1(c)所示，在此基础上，逐步演化出多种变形.对于单边磁体构型，从不同角度可进行不同分类.如按检测区域磁场方向可分为平行磁体表面与垂直磁体表面两种；按照检测区域的磁场均匀性可分为均匀区检测和非均匀区检测.具体磁体几何结构也分为U形(U-shaped)磁体、条形磁体等几种.从应用来分，有测量弛豫扩散分析用、成像用以及波谱分析用[1-3].
磁体设计是单边核磁共振系统中的关键技术，往往借助于数学仿真技术实现不同的磁场要求.主要原则是以最小的磁体重量实现尽可能大的均匀区域和最大检测灵敏区域.这种优化主要聚焦于磁极间隙的优化或者确定某种合适的磁体构型和磁极方向.另一个关键技术是单平面射频线圈技术，不同的单边磁体适配于不同形状的射频线圈.B0与磁体表面平行的单边磁体需要垂直于磁体表面的B1场，因此一般采用单向电流环（口字形或圆形）射频线圈来产生所需射频场.而B0与磁体表面垂直的单边磁体需要平行于磁体表面的B1场，往往采用至少两个反向电流环（8字形或田字形）射频线圈来产生所需射频场[1-3].
2008年，德国亚琛大学的Blumich B教授团队基于单边磁体开发了便携式核磁共振鼠标(NMR mobile universal surface explorer，NMR MOUSE)，大小为30 cm×30 cm×10 cm，重量36 kg[1, 4].此后，其团队成员进行了持续开发，逐步缩小磁体体积和电子学系统大小，最近实现了Micro MOUSE系统，其磁体尺寸仅2.8 cm×2.8 cm×3.1 cm，重量为0.8 kg，可实现0.2 mm的检测厚度[1].Blumich教授因为这些开创性工作及其单边核磁共振系统专著，其也被尊称为“单边核磁共振系统之父”.
国内见诸文献的单边核磁共振技术的研究中有中国科学院电工研究所夏平畴教授和他的博士研究生车文华于2000年提出“薄片型医用非常规核磁共振成像仪磁体”，相关博士论文于2002年完成.该论文提出单边磁体模型，设计的磁体样品灵敏区域大小为1.5 cm×l.2 cm，场强0.06 T.尽管其磁场强度较低，均匀区面积很小，距离医学诊断目的还有很大差距，但开始了这方面可贵的探索[5, 6].此外，浙江大学姚缨英老师指导的研究生谢俊鹏于2006年完成了“完全开放方式磁共振成像磁体的设计”的硕士论文，对单边成像磁体的设计进行了详细论述[7].中国石油大学的肖立志教授团队应用单边磁体系统实现了三维T1-T2-D的测量，并在石油领域中重油成分分析的应用研究，取得了较好的效果[8].
重庆大学徐征课题组与英国诺丁汉大学合作，采用半环Halbach磁体形成的单边逸散磁场，集成新西兰magritek公司的电子学部件，搭建了单边便携式核磁共振系统（磁场梯度为2 T/m）并进行输电线路中的复合绝缘子老化的在线检测研究[9].
单边磁体系统的样品探测深度是影响其应用拓展的重要因素.在一些应用领域，比如对包装食品的无损检测中，包装厚度往往超过1 mm，因此需要至少超过2 mm的检测深度才能满足应用需求.样品探测深度与自然梯度大小成反相关关系，故单个线圈的检测深度都在2 mm以下，通过多个线圈的组合更换实现较大的探测深度.
本研究从分析核磁共振基本技术条件出发，推导出非均匀磁场条件下的核磁共振技术条件，通过对已有单边磁体产生的逸散磁场特性分析，得出射频场设计目标，设计单边平面射频线圈，以实现大体度磁场下实现较大的探测深度目标，搭建实验系统并进行相关实验效果验证，为全开放便携式核磁共振分析仪器积累经验、技术和应用基础.
1 单边全开放式核磁共振技术分析
1.1 单边磁体产生的磁场特征分析与技术条件
核磁共振的物质条件包括3个方面：自旋核、磁场、射频场；技术条件有两个：1）射频场(RF)与磁场(B0)正交，即RF⊥B0；2）射频频率(f)与磁场确定的自旋核进动频率相等，即$ f = \gamma {B_0} $，γ为自旋核的旋磁比.
常规核磁共振系统的主磁场B0是高度均匀（ppb/1mmDSV量级）的，对射频场的要求不高，因此检测难度相对较小.单边磁体系统也有通过各种匀场手段在磁体一侧实现高度均匀的微小区域以满足应用（一般用于全开放式波谱研究），如甜点型(sweet pot)，但更多的单边磁体则是在非均匀磁场条件下进行信号的检测与应用.
本项目采用的磁体是两块间距16 mm的钕铁硼(NdFeB)材料的磁极在一块铁基板上形成的U型结构，如图 2所示.该构型单边磁体产生的磁场极度不均匀，其非均匀性体现在两个方面：1）磁场大小不同，2）磁场方向不同[1, 3, 9].以本研究所采用的单边磁体产生的磁场为例，如图 2所示，(a)为磁体外观，(b)为磁体及其磁场等高线（水平面定义为y=0）.其磁力线分布示意图如图所示，平面以上区域（即样品区域）内沿x不同位置的磁场方向是逐渐变化的，从正中区域(x=0)处开始向右是+x向（朝向S极），向左是-x向（朝向N极）.水平面向上是+y向，向下是-y向.不仅如此，相同的x位置，沿着y向，其磁场大小也是变化的.以x=0处不同y高度的磁场大小如表 1所示，样品检测区域内，高度增加1 mm，场强减小0.01 T，即沿+y向存在一个梯度为10 T/m (即100 G/mm)的恒定梯度磁场.由此可知该磁场的均匀性至少劣于20 000 ppm/1 mmDSV，相对常规磁共振均匀性差数十万倍之巨.水平面以下的区域为两磁极之间的沟槽，几何尺寸为16 mm×30 mm×128 mm.
表 1 不同等高线上的磁场数据及梯度(y=0为磁体水平面，单位mm)
Table 1 The magnetic field data and gradient of different contour lines (y=0 is the magnet plane, unit: mm)
| 等高线沿y轴/mm |
场强/(10-4 T) |
梯度沿y轴/(0.1 T/m) |
等高线沿x, z轴的
区域/mm |
| -8 |
5240.0 |
| 16×16 |
| -7 |
5232.6 |
| 16×16 |
| -6 |
5200.7 |
| 16×16 |
| -5 |
5150.6 |
| 16×16 |
| -4 |
5064.3 |
| 16×16 |
| -3 |
4986.6 |
| 16×16 |
| -2 |
4901.8 |
| 16×16 |
| -1 |
4808.6 |
| 16×16 |
| 0 |
4712.4 |
| 16×16 |
| 1 |
4609.4 |
103 |
64×40 |
| 2 |
4508.4 |
101 |
64×40 |
| 3 |
4404.2 |
104 |
64×40 |
| 4 |
4300.9 |
103 |
64×40 |
| 5 |
4193.5 |
107 |
64×40 |
| 6 |
4086.2 |
107 |
64×40 |
| 7 |
3981.0 |
105 |
64×40 |
| 8 |
3876.5 |
105 |
64×40 |
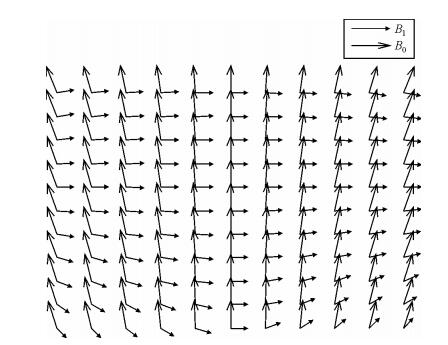
要在如此非均匀的磁场下满足核磁共振条件，实现大范围的核磁共振，需要射频场能在尽量大的区域内满足两个核磁共振技术条件：一方面在尽量与主磁场正交，同时射频频率与拉莫尔频率相等，如图 3所示.
1.2 单边磁体非均匀磁场上的射频场强度要求
均匀磁场条件下，一般对射频场强度的要求不严格，射频强度不足，可以通过时间累积达到相同的射频激励效果.但在非均匀磁场中，除了满足方向正交和频率相等的条件外，对于射频场强度有着严格要求[10-13].我们以激励检测厚度为h的样品作为射频场强度的设计目标来分析：
h厚度内的质子进动频率范围为$ \Delta f = \gamma Gh $，G为自然梯度，γ为旋磁比.为保证激励有效，射频信号带宽Bw至少要大于Δf，即$ {B_w} \ge \Delta f $.
核磁共振分析技术一般采用硬脉冲，其时域为方波调制波形，对应频域为SINC波形，方波宽度τ与频带Bw之间遵循$ \tau = \frac{{1.21}}{{{B_w}}}
$，故有$ \tau \le \frac{{1.21}}{{\gamma Gh}} $，即射频脉宽不能超过某值.
方波脉宽τ与射频角度θ之间又遵循$ \theta = 2\pi \gamma {B_1}\tau $的关系，B1为射频场强度.在硬脉冲CPMG(Carr-Purcell-Meiboom-Gill)序列中，180°和90°激励脉冲都需要满足脉宽极值要求，所以取θ=π.由上可知，$ {B_1} \ge Gh/2.42 $.由此式可知，自然梯度越大，所需要的射频场强度越高；要实现检测深度越深，也需要越高的射频场强度.
1.3 单边磁体恒定梯度磁场下的扩散测量技术
非均匀磁场中，无法检测到FID序列，一般只应用CPMG序列实现信号采集和分析.采集到的CPMG信号经拉普拉斯变换可得到信号的T2弛豫谱，基于谱的信息（比如峰数、峰位、峰下面积），同样可以分析样品的各种物性参数，比如水分相态、各相态含量、油水比例、橡胶交联密度、孔隙度与孔隙尺寸分布等等[1-3, 14-17].
相比常规核磁共振系统，单边核磁共振设备除了便携、成本低的特点之外，另一个优势就是可轻易实现扩散系数D的测量，以及实现D-T2[14]或者是D-T2-T1测量[8].
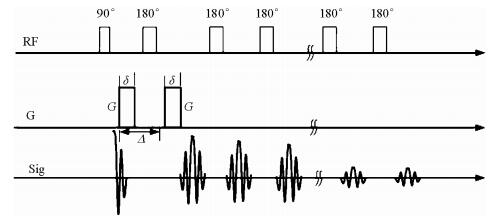
传统核磁共振采用脉冲梯度场来测量D，尽管有很多变形和改进，但其本质上都是PGSE (Pulsed Gradient Spin Echo)序列.PGSE序列是在基本SE序列中180°射频两边对称施加一对强梯度磁场.采用梯度磁场进行扩散弛豫系数测量，其实质是检测梯度磁场对扩散运动的氢质子导致的散相效果.如图 4是将PGSE与CPMG序列结合起来实现D-T2二维谱测量.
为实现较小扩散弛豫的测量，需要增加脉冲梯度G.在一些需要实现油气水区分的应用领域，甚至需要高达4 T/m的梯度磁场[18].要产生如此巨大的梯度磁场，需要施加300 A的脉冲电流，这需要配备笨重且昂贵的梯度功放系统.除此之外，巨大的电流切换还会在磁极板和周围导磁材料上产生巨大的涡流.为消除涡流的影响需要采用预加重技术和自屏蔽梯度线圈.自屏蔽梯度线圈会极大减弱有效梯度场的强度，预加重技术调节非常麻烦，预加重参数还因样品和梯度幅值变化而不同，故只能尽量减小不能完全消除涡流的影响.
单边磁体产生的磁场本身就存在一个巨大的恒定梯度磁场，如本研究中这个自然梯度高达10 T/m，且没有任何涡流的影响.与脉冲梯度不同的是，梯度磁场一直存在，扩散弛豫导致的幅值衰减效应也会一直存在.应用恒定梯度实现D-T2的序列称为SGSE-CPMG(static gradient spin echo CPMG)，其CPMG回波串的衰减T2遵循以下规律[18]：
|
$
\frac{1}{{{T_2}}} = \frac{1}{{{T_{2s}}}} + \frac{1}{{{T_{2B}}}} + \frac{1}{{{T_{2D}}}} = \rho \frac{S}{V} + c\frac{\eta }{T} + \frac{{D{{(\gamma G{T_E})}^2}}}{{12}}
$
|
(1) |
(1)式中等式右边第一项为样品的表面弛豫$ (\frac{1}{{{T_{2s}}}}) $，与样品的湿润相和样品的成分有关，决定于比表面积(S/V)，反映了孔隙尺寸和孔隙结构；第二项为体弛豫$ (\frac{1}{{{T_{2B}}}}) $，即本征弛豫，反映了分子所在的流体粘度(η)和温度(T)；第三项就是扩散弛豫$ (\frac{1}{{{T_{2D}}}})$，与扩散系数(D)、恒定梯度(G)、回波时间(TE)相关.
本研究中使用样品不是多孔介质样品，可以认为其没有表面弛豫.对于已知本征弛豫的样品，应用SGSE-CPMG序列测量得到总体弛豫T2，恒定梯度G如果已知，TE已知，根据后文(2)式即可得到扩散弛豫D.同理，将该序列循环测量，每次设定不同的TE，对不同TE下获得T2回波串数据形成的二维数组进行二维逆拉普拉斯变换既可得到D-T2二维谱.
2 单边核磁共振系统测试
2.1 探头设计
单边射频线圈的设计需要综合考虑线圈几何形状、射频激励范围、射频强度以及射频场方向等多个因素.为满足B1与B0正交，射频线圈只能采取单环形状，如口字形或圆形.在此基础上，要使激励范围大，需要使B1与B0尽可能正交的区域大.而激励范围与射频场强度是一对矛盾，因此射频线圈的包围面积也需要通过仿真合理确定.通过HFSS和Maxwell软件仿真得知，相同面积的圆形线圈比矩形线圈实现的激励区域要大，且均匀性较好控制，口字形线圈可在中心点实现较大的射频场强度，但在拐角处的射频场方向性和均匀性不好.同时为了更好的利用平面以上的高场强区域，线圈需要能嵌入到磁极间隙中.
线圈匝数方面，可以用小电流的多匝线圈产生的射频叠加实现目标射频场要求，由于区域有限，导线宽度小和绕线长、电阻大、发热量大，并且导线间的分布电容影响也较大，故采用单匝粗导线来绕制线圈，其线圈电感小，探头死时间短，同时导线电阻小，发热量影响也小.
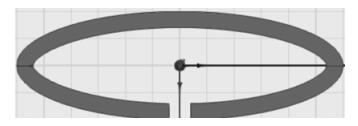
基于上述分析和仿真，最终实现了单匝椭圆形射频线圈，线宽考虑到多匝基于上述要求，最后设计成一个椭圆形线圈如图 5所示.该线圈长轴为60 mm，短轴为10 mm，线宽为1.5 mm，这样理论计算和仿真软件结果均显示，线圈上通过100 A电流，在磁体表面1 mm高度的位置可产生0.07 T射频场.设计好的单匝线圈最后应用环氧树脂(FR-4)材料制成PCB板，厚度1.6 mm.PCB板材对于射频线圈的衬底效应在使用HFSS和Maxwell建模仿真时也考虑进去的.
线圈设计制作成功后，还需要进行调谐匹配的设计.图 5所示线圈的等效电感为142 nH，等效电阻0.1 Ω.本研究采用串联谐振模式，应用multisim10电路仿真软件进行调谐匹配参数的仿真计算，最终仿真结果为调谐电容0.650 nF，匹配电容2.06 nF.谐振频率19 MHz，Q值24.332 dB.调谐匹配单元和线圈组成探头，封装在一个屏蔽盒内，卡在磁极板间隙沟槽内，线圈平面刚好与磁体平面齐平.最终探头测试其90°脉宽2.5 μs，系统死时间10 μs，最短可实现15 μs的半回波时间采集信号.
2.2 系统搭建
搭建的单边磁体的核磁共振系统，包括单边磁体（单边磁体的尺寸为178 mm×128 mm×105 mm，磁体中心有16 mm×30 mm的沟槽，磁体表面场强为0.5 T，磁体采用钐钴材料，对检测之外的区域具有磁体自屏蔽功能），自行开发设计的探头，射频功放（中心频率20 MHz，300 W），前置放大器（中心频率20 MHz，最大增益56 dB），谱仪系统（苏州纽迈公司生产的Meso-MR二代谱仪）.
主要采集参数：SGSE-CPMG序列，90°脉宽P1=3 μs，180 脉宽P2=6 μs，采样带宽SW=300 kHz，重复时间TW=500 ms，半回波时间DL1=0.015 ms.样品分别采用了不同浓度的硫酸铜溶液，食用油和纯水.
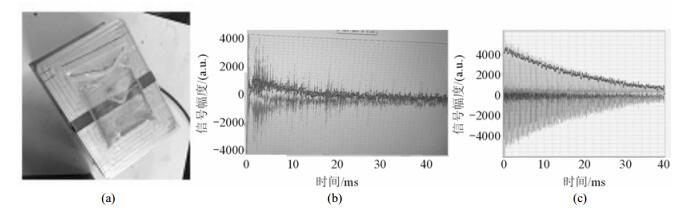
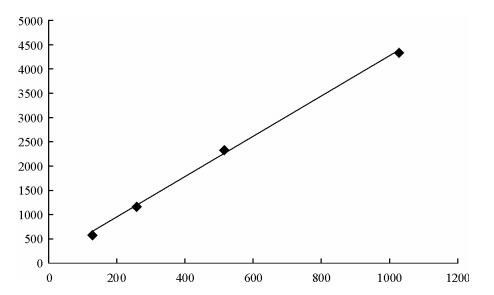
2.3 核磁共振信号累加次数-幅值线性关系
图 6为磁体与样品之间的关系.样品为塑封带包装的1%硫酸铜水溶液，图 6(b)为最初获取的疑似信号.图 6(c)为累加次数(NS)等于1 024次时的信号，信噪比明显得到优化.为验证该疑似信号是否为核磁共振信号，其他参数不变，通过改变NS，察看首点信号幅值如表 2，对数据进行拟合如图 7所示.由表和图可知累加次数与信号幅值之间存在着严格的线性关系，由此可确认采集信号为核磁共振信号.
表 2 不同累加次数CPMG信号第一个峰值的幅值
Table 2 Different number of cumulative and its first peak amplitude of the CPMG signal
| NS（累加次数） |
首点峰值 |
| 128 |
600 |
| 256 |
1200 |
| 512 |
2350 |
| 1024 |
4350 |
2.4 信号检测深度
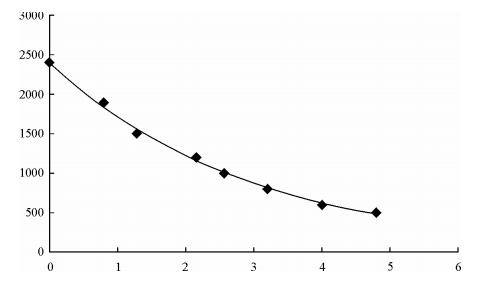
由于单边核磁共振系统在y轴方向有着一定的梯度，造成拉莫尔频率差异很大，而射频信号是有带宽的，且射频场强度沿y向也是快速衰减的，因此只能在一定区域内满足核磁共振条件，也就是说样品是有检测范围的.相对于xz平面内的检测范围，对于y向的检测高度（样品探测深度）对于应用而言更加重要.为了探究该单边核磁共振系统的探测深度，采用在磁体和样品中间添加含氢质子的聚四氟乙烯材料，逐步抬高样品进行信号采集.样品抬高高度与首点信号幅值之间的变化如表 3所示.经拟合后发现随着样品高度提高，相同检测参数下信号幅值指数衰减，图 8所示.抬高到4.8 mm后，1 024次采集的信号基本处于弛豫反演算法对信噪比的最低要求，由此确定探测深度小于5 mm.
表 3 单边核磁共振系统探测深度实验峰值变化
Table 3 Peak changes of unilateral NMR system probing depth experiments
| 高度/mm |
信号峰值 |
高度/mm |
信号峰值 |
| 0 |
2400 |
2.56 |
1000 |
| 0.80 |
1900 |
3.20 |
800 |
| 1.28 |
1500 |
4.00 |
600 |
| 2.16 |
1200 |
4.80 |
500 |
2.5 均匀磁场与非均匀磁场下的T2弛豫时间的差别
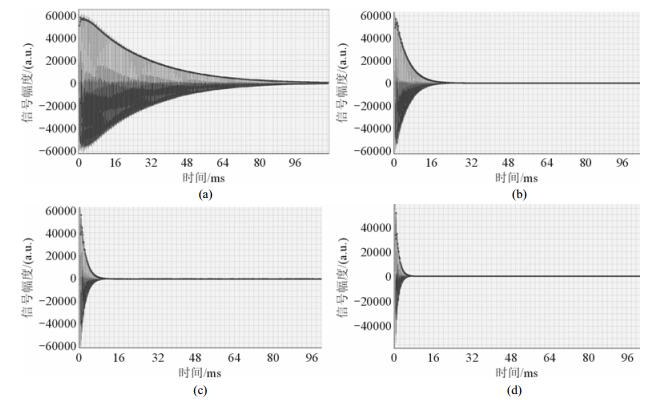
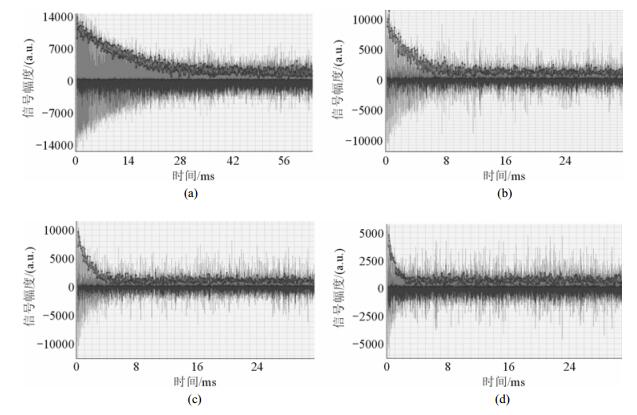
为验证相同样品在均匀磁场和非均匀磁场中的测量结果差异性，我们准备了浓度分别为1%，5%，10%，15%的硫酸铜水溶液，分别在均匀磁场和单边逸散磁场中利用单平面射频线圈进行了CPMG信号采集和T2反演.应用同一个单平面线圈，在双极型磁体中和单边磁体上的采集模式分别如图 9(a)，(b)所示.均匀磁场下采集到的信号如图 10(a)~(d)所示，横轴为采样时间，单位ms，4种浓度样品应用相同的采样时间，图中可明显看出，浓度越高，弛豫时间越短.单边磁体上的信号如图 11(a)~(d)所示，由图可看出，采样时间相同，尽管信噪比相比均匀磁场下的信号有明显降低，但信号的衰减仍然体现出与均匀磁场中完全相同的规律：浓度越高，弛豫时间越短.
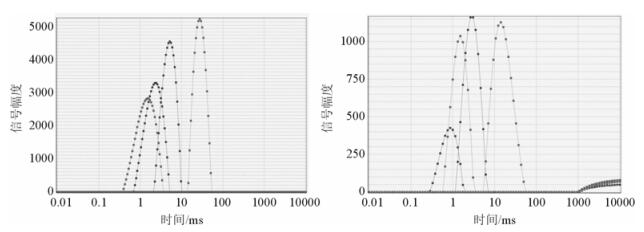
图 12所示为均匀场核磁共振和单边磁场下的CPMG信号T2谱反演结果对比.二者均体现出弛豫时间随浓度递减的规律.尽管定性上是吻合的，但定量分析两组信号的弛豫谱细节（如表 4所示）可发现，均匀磁场和非均匀磁场中，相同浓度的硫酸铜溶液其T2时间是不同的，其差异就是单边磁体自然梯度下扩散弛豫效应导致的，这也是扩散弛豫测量的机理.同时还可看出单边磁体上的信号峰下面积衰减较快，原因在于短弛豫信号在自然梯度下衰减过快，导致采集到信号减小.故单边磁体系统如要进行定量分析，还需要进行弛豫校正和梯度校正.同时可以看到，单边磁体的谱峰尾端出现了由于信噪比低导致的噪声峰.
表 4 均匀场核磁共振和单边核磁共振系统反演数据的对比
Table 4 The Contrast of inversion data between uniform field NMR and unilateral NMR
| 场 |
浓度 |
起始点 |
峰点 |
结束点 |
峰面积 |
双极型
均匀磁场 |
1% |
13.667 |
27.364 |
54.1789 |
64040.432 |
| 5% |
2.097 |
5.171 |
10.353 |
63094.690 |
| 10% |
0.644 |
2.409 |
5.171 |
58219.657 |
| 15% |
0.370 |
1.482 |
3.654 |
55000.397 |
单边非
均匀磁场 |
1% |
5.337 |
14.175 |
57.224 |
10862.085 |
| 5% |
1.510 |
3.054 |
7.055 |
8914.301 |
| 10% |
0.572 |
1.520 |
3.511 |
7838.135 |
| 15% |
0.248 |
0.870 |
2.009 |
3474.404 |
2.6 扩散系数测量单边磁体的梯度
对于容积型样品，不考虑表面弛豫，理论上只要自然梯度G已知，分别测量出SGSE-CPMG序列下的T2和本征T2B，即可通过(2)式：
|
$
\frac{1}{{{T_2}}} = \frac{1}{{{T_{2B}}}} + \frac{{D{{(\gamma G{T_E})}^2}}}{{12}}
$
|
(2) |
计算出扩散系数D.但与人为施加脉冲梯不同的是，单边磁体产生的自然梯度除了沿y向上存在（本研究中为10 T/m），同时沿x和z向均存在着梯度变化.仅使用y向梯度进行D的计算，会使计算结果偏大.对梯度场进行仿真和校正后可实现有效测量，这个难度较大.本项目通过已知扩散系数的样品信号计算出单边磁体的整体自然梯度G，再进行相应样品的扩散测量.
采用已知T2B=1 500 ms的水样品，扩散系数D=2.58×10-9 m2/s（20℃条件下），在单边磁体上应用SGSE-CPMG序列采样，采用不同的半回波时间DL1进行信号采集，采集信号并进行反演得到T2弛豫峰位，最后根据(2)式计算出G，其中TE=2DL1+P2.具体参数和计算结果如表所示，由表 5可知，3种参数下，计算G的大小非常接近（误差可能来自于温度不同导致扩散系数的差异），均值在15.3 T/m，说明应用不同的参数测量得到的G梯度是吻合的，结果还说明，除了沿y向的10.3 T/m的梯度外，磁场在xz平面内还存在着10.6 T/m的梯度磁场.
表 5 相同的水样在不同采集参数下计算得到的G值
Table 5 G values of the same water samples at different acquisition parameters
| DL1/μs |
P2/μs |
TE/μs |
T2峰位/ms |
G/(T/m) |
| 20 |
6 |
46 |
113.113 |
15.69 |
| 40 |
6 |
86 |
34.063 |
15.00 |
| 50 |
10 |
110 |
23.509 |
15.85 |
2.7 未知样品的扩散测量
应用2.5节得出的实际G，可测量未知样品的扩散系数.如对上述1%, 5%, 10%, 15%的硫酸铜水溶液，通过其在均匀场和梯度场中的T2峰值差异，应用(2)式分别计算得到其扩散系数如表 6所示：
表 6 计算得到不同浓度的硫酸铜溶液的扩散系数D
Table 6 Calculated for different concentrations of copper sulphate solution diffusion coefficient D
| 样品浓度 |
T2B(均匀磁场/ms) |
T2(恒定梯度磁场/ms) |
D/(×10-9 m2/s) |
| 1% |
27.364 |
14.175 |
4.66 |
| 5% |
5.171 |
3.054 |
18.4 |
| 10% |
2.409 |
1.52 |
33.3 |
| 15% |
1.482 |
0.87 |
65.1 |
由表 6可知，硫酸铜的浓度越高，水分子的扩散系数越高，呈线性关系，即弛豫剂金属离子会加速水分子的扩散.这其实也可以从另一个角度得到合理的解释：离子浓度增加，会在样品内部形成一个梯度磁场，也就是变相增加梯度磁场，从而缩短弛豫.
本研究还以食用大豆油作为样品进行了验证测量.均匀场核磁共振下T2弛豫时间为85.97 ms, 可视为食用油的本征T2时间.由于油的扩散系数很小，故在单边系统下的T2弛豫时间为84.526 ms，通过计算得到，食用油在扩散系数为2.78×10-11 m2/s.计算结果与已知扩散系数非常接近.
3 总结与展望
本研究从核磁共振基本技术条件出发，研究了非均匀磁场下的核磁共振技术条件，确定射频场目标，设计单平面射频线圈，搭建了一套单边核磁共振技术实验系统.应用该系统，进行了CPMG信号采集、探测深度等实验，并利用单边磁体的自然梯度磁场，开展了恒定梯度磁场下的扩散测量方法探索.
该系统可在15.3 T/m的自然梯度磁场下，实现接近5 mm厚度的信号检测，能满足相关应用领域的全开放式检测深度需求，后续将针对不同领域开展应用方法的研究. 全开放式单边核磁共振系统作为核磁共振家族对样品几何形状和尺寸要求最小的一种系统，有着广阔的发展前景，不仅仅在测量液体扩散系数方面，同时在食品安全，文物保护，人体表面成像等领域都有着巨大潜力.
2014, Vol. 31
表1(Table 1)
