文章信息
- 袁峰, 王鹏飞, 孔飞, 许祥坤, 石发展, 杜江峰
- YUAN Feng, WANG Peng-fei, KONG Fei, XU Xiang-kun, SHI Fa-zhan, DU Jiang-feng
- 金刚石固态量子计算中的高分辨率成像
- Super-Resolution Imaging in Diamond Solid-State Quantum Computation
- 波谱学杂志, 2014, 31(4): 449-464
- Chinese Journal of Magnetic Resonance, 2014, 31(4): 449-464
-
文章历史
收稿日期: 2014-04-02
收修改稿日期: 2014-10-30


显微镜自其发明以来,便成为人们探求微观世界必不可少的工具.
19世纪70年代,德国物理学家恩斯特·阿贝(Ernst Karl Abbe)提出光学衍射极限的说法[1],指出由于受到光波衍射的影响,传统光学显微镜所能达到的极限分辨率约为光波波长(llλlll)的一半.随后又提出分辨率(d)反比于显微镜数值孔径(NA),并且验证了公式
| $ d = \frac{\lambda }{{2NA}} $ | (1) |
以可见光为媒介的远场光学显微镜分辨率不可能突破百纳米量级的观点被普遍接受.
经过近百年发展,近场扫描光学显微镜(NSOM)[2, 3]已经可以获得小于25 nm的分辨率;各类电子束显微镜和其他扫描探针显微镜相继诞生,并且分辨率已达到原子级别(10-1 nm)[4].然而在生命科学、医疗等领域,以可见光和透镜为基础的传统光学显微镜始终占据着重要地位.这主要是由于使用电子束显微镜容易对生物活性样品造成损害,而各类扫描探针显微镜和近场显微镜只能做到样品的表面成像,相对于它们而言,远场光学显微镜具有独特优势:以可见光作为信息载体,观测更为直观;可透过样品表面对样品内部进行直接观察,为样品内部结构的三维(3D)成像提供了可能性;借助于荧光标记等技术可以对样品特定内部结构和生化进行针对性的观察.因此,若能构建具有可见光亚光波波长分辨率的远场光学显微镜,将会开启探求微观世界的新篇章.
增大显微镜数值孔径的常用方法之一是将折射率较大的镜油或其他一些有机物质填充于物镜与样品之间.然而填充物折射率与样品折射率往往不能做到完全相同,导致光波在样品表面发生折射,影响显微镜成像品质.实验上已经验证,使用固体浸没透镜(Solid immersion lens, SIL)[5, 6]是解决媒介折射率与样品折射率不匹配的有效方法.
20世纪中期,几种被认为是“进一步推进了衍射屏障”(pushing the diffraction barrier)的成像方法被相继提出,共聚焦显微镜[7, 8]就是其中之一.1955年,Marvin Minsky利用共聚焦原理搭建了第一台共聚焦显微镜;1957年,他申请了共聚焦显微镜的专利;1970年,第一台单光束共聚焦激光扫描显微镜问世.
不同于传统光学显微镜的直接平面成像模式,共聚焦显微镜对样品进行逐点成像.它在激发光路和收集光路中各添加有小孔(Pinhole),激发光路的小孔用来产生小而精细的点光源;而收集光路的小孔确保只有焦平面邻近区域所发出的荧光能够到达探测器,大幅提高所成图像质量.
另外还有基于干涉原理构建的4Pi显微镜[9]和I5M显微镜[10];然而遗憾的是,虽然较传统远场光学显微镜而言,以上几种显微镜在分辨率有了一定的提升,但它们并没有在真正意义上地突破衍射极限的限制,只是“将衍射屏障推进到了一个更小的尺度”.
直到20世纪末,随着受激发射损耗(STED)[11]和基态损耗(GSD)[12]等以可逆饱和光学荧光跃迁(RESOFLT)[13]为基础思想的显微镜概念的提出,远场荧光显微镜才进入了另一个新的发展阶段.
本文简要介绍受激发射损耗(STED)显微镜和基态损耗(GSD)显微镜以及金刚石NV色心固态量子计算方法,概述金刚石固态量子计算中超分辨成像的最新研究进展.
1 突破光学衍射极限RESOFLT可逆饱和光学荧光跃迁(RESOFLT),也被称为目标开关与读取显微技术,是一类超高分辨率显微镜的总称.主要包括受激发射损耗显微镜、基态损耗显微镜、饱和图案激发显微镜(SPEM)以及饱和结构光照明显微镜(SSIM)等几种.虽然它们以可光见作为媒介,却可以得到不受衍射极限限制的超高分辨率.
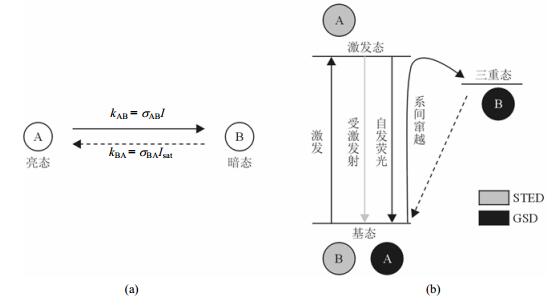
要利用RESOFLT方法获得超高分辨率,所用荧光染料分子必须具有两个(以上)可区分状态:A和B;如图 1(a),荧光分子可以在这两个状态之间反复来回跃迁并且其中至少一个跃迁是可以由光学手段来触发.图 1(b)显示了两种不同RESOFLT方法的成像原理图.
通常将能够发出系统可识别信号(如荧光)的状态称之为亮态(Bright State),标记为A;另一个不能发出可识别信号的状态称为暗态(Dark State),标记为B.一般情况下,从亮态A到暗态B的跃迁可以由光触发;而从暗态B到亮态A的跃迁触发形式可以是另一个波段的光,也可以是热能或是某种化学反应等等,甚至也可以是自发辐射.当然,亮态和暗态互换角色时,RESOFLT的方法仍然可行,只不过此时得到的图像是所谓的“负像”(negative image),需经过图像去卷积(deconvolution)处理[14]后才能得到正图像(positive image).
如图 1(a)所示,现假设从亮态A到暗态B的跃迁由入射光驱动,其跃迁速率为kAB(x)=σABI(x),其中σAB是光作用截面大小,I(x)是入射光功率,是空间坐标x的函数.相应地,用kBA表示从B到A的跃迁速率;NA和NB分别表示归一化后的处于状态A和状态B的分子数密度.当入射光照射在样品上时,有:
| $ {\rm{d}}{N_{\rm{A}}}/{\rm{d}}t =-{\rm{d}}{N_{\rm{B}}}/{\rm{d}}t = {k_{{\rm{BA}}}}{N_{\rm{B}}}-{k_{{\rm{AB}}}}{N_{\rm{A}}} $ | (2) |
在经过一段时间
| $ N_{\rm{A}}^\infty = {k_{{\rm{BA}}}}/({k_{{\rm{AB}}}} + {k_{{\rm{BA}}}}) $ | (3) |
结合(2),(3)式可以看出,当
RESOFLT采用一束含有一个(或多个)“功率零点”xi的非均匀入射光束照射在样品上,这样一来,只有在功率零点xi的邻近区域(I < Isat)内的荧光分子处于状态A;在I≥Isat的区域内,荧光分子处于状态B.当然,在实验中要做到
利用RESOFLT原理所构建的各类显微镜所能达到的最小分辨率可以统一写成[16]
| $ \Delta d = \frac{\lambda }{{2n \cdot \sin \alpha \cdot \sqrt {1 + I/{I_{{\rm{sat}}}}} }} $ | (4) |
(4)式中n为样品物质折射率,α为所用物镜的孔径角大小;定义饱和度
STED的概念由Hell S W等人于1994年首次提出[11],是最早提出的基于RESOFLT概念的远场荧光显微技术.1999年,Klar T A与Hell S W完成了STED的第一个实验[17],并获得了100 nm左右的分辨率.经过近20年的发展,STED显微成像技术已经可以实现纳米尺度的成像[18, 19].
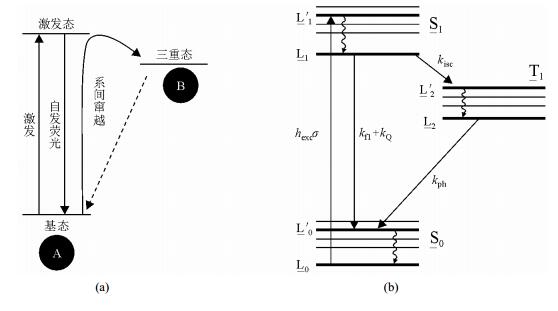
STED采用两束光(激发光和STED光)照射到样品上,将基态S0看作暗态B,激发态S1看作亮态A.如图 2(a),激发光均匀地照射在样品上,使荧光分子从基态跃迁到激发态.处于激光态的荧光分子回到基态的方式有两种:受激发射和自发荧光辐射.通常而言,自发荧光辐射需要约数十纳秒时间,STED光利用非均匀光束,它的作用正是促使其照射区域内处于激发态的荧光分子在自发辐射之前通过受激发射的形式回到基态.二者经过同轴共焦调节,便构成了RESOFLT系统,如图 2(c)所示.
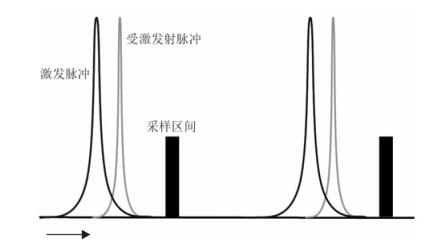
根据所使用激光器的不同,STED可以分为脉冲STED和连续波STED.早期的STED模型中所使用的激光器均为脉冲激光器,激发光和STED光采用同频率不同展宽的两束光波.STED光波长略大于激发光波长以保证完全消光.如图 3所示,工作时,脉冲序列为“激发光-STED光-采样-激发光-STED光-采样……”,如此循环.
|
| 图 3 STED脉冲序列 Fig. 3 Pulse sequence of STED |
如图 2(b)所示,L0, L1, L2, L3分别为荧光染料分子的基态底能级,激发态上能级,激发态底能级和基态上能级;令ni(t)分别为时刻t位于各能级Li(i=0, 1, 2, 3)上荧光染料分子的概率分布.各能级瞬时分布可以由公式确定为[11]
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{n_0}}}{{{\rm{d}}t}} = {h_{{\rm{exc}}}}{\sigma _{01}}({n_1}-{n_0}) + \frac{1}{{{\tau _{{\rm{vibr}}}}}}{n_3}\\ \frac{{{\rm{d}}{n_1}}}{{{\rm{d}}t}} = {h_{{\rm{exc}}}}{\sigma _{01}}({n_0}-{n_1})-\frac{1}{{{\tau _{{\rm{vibr}}}}}}{n_1}\\ \frac{{{\rm{d}}{n_2}}}{{{\rm{d}}t}} = \frac{1}{{{\tau _{{\rm{vibr}}}}}}{n_1} + {h_{{\rm{STED}}}}{\sigma _{23}}({n_3} - {n_2}) - (\frac{1}{{{\tau _{{\rm{fl}}}}}} + {k_{\rm{Q}}}){n_2}\\ \frac{{{\rm{d}}{n_3}}}{{{\rm{d}}t}} = {h_{{\rm{STED}}}}{\sigma _{23}}({n_2} - {n_3}) + (\frac{1}{{{\tau _{{\rm{fl}}}}}} + {k_{\rm{Q}}}){n_2} - \frac{1}{{{\tau _{{\rm{vibr}}}}}}{n_3} \end{array} \right. $ | (5) |
另外还有
为了确保荧光染料分子能够顺利地以受激发射形式从L2→L3,所用STED光的脉冲长度应该远小于荧光寿命
相较于脉冲STED而言,连续波STED显得简单许多.虽然连续波STED没有脉冲STED那么高的峰值STED光功率,但脉冲激光器往往价格昂贵,且脉冲同步对硬件方面和技术层面都有很高的要求.
2007年,Willig K I等人利用连续波激光器成功搭建了STED显微镜[20],获得了30 nm左右的分辨率.当采用连续波激光作为光源时,荧光染料分子的能级分布达到动态平衡
| $ \left\{ {\begin{array}{*{20}{c}} {{n_{\rm{A}}} = \frac{{{k_{{\rm{BA}}}}}}{{{k_{{\rm{BA}}}} + {k_{{\rm{AB}}}} + {k_{{\rm{fl}}}}}}}\\ {{n_{\rm{B}}} = \frac{{{k_{{\rm{AB}}}} + {k_{{\rm{fl}}}}}}{{{k_{{\rm{BA}}}} + {k_{{\rm{AB}}}} + {k_{{\rm{fl}}}}}}} \end{array}} \right. $ | (6) |
(6)式中,nA,nB分别是动态平衡时荧光分子处于状态A和状态B的概率;kAB,kBA分别为荧光分子由状态A跃迁到状态B以及由状态B状态到状态A的跃迁速率;kfl为荧光发射速率.
2011年,Hell S W等人提出混合型STED[21]设计方案:使用脉冲光作为激发光而STED光则用连续波激光.这种方案既结合脉冲STED和连续波STED二者的优势又容易实现.
1.2 基态损耗(GSD)Hell S W在提出STED的一年后,又提出了GSD显微镜的概念[12].第一台GSD实验装置于2006年搭建成功并获得20 nm的成像分辨率[22].与STED相比,GSD的原理更为复杂一些,如图 4(a),GSD需要利用到处于基态和激发态的一个三重态T1,它将基态看作是状态A,三重态看作是状态B.处于激发态的分子有一定几率通过系间窜越(intersystem crossing, ISC)形式到达三重态,三重态是亚稳态,之后分子经由三重态自发辐射作用回到基态,这一过程即为磷光发射过程,该过程并不会发出荧光.由于三重态寿命(磷光寿命)τph远长于荧光寿命τfl,这样只要在τph时间尺度范围内,加快分子在基态和激发态之间的循环速率,便可以实现分子在三重态的富集[12].
如图 4(b)所示,L0, L0', L1, L1', L2, L2'分别为荧光染料分子的基态底能级,基态上能级,激发态底能级,激发态上能级,三重态弛豫振荡能级和三重态直接激发能级;令ni(t)为时刻t位于能级Li(i=0, 1, 2)上荧光染料分子的概率分布.由于弛豫振荡时间一般都处于皮秒量级,故不再考虑各直接激发能级,而只考虑弛豫振荡能级上的分子分布.各能级瞬时分布公式[9]为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{n_0}}}{{{\rm{d}}t}} =-{h_{{\rm{exc}}}}\sigma {n_0} + ({k_{{\rm{fl}}}} + {k_{\rm{Q}}}){n_1} + {k_{{\rm{ph}}}}{n_2}\\ \frac{{{\rm{d}}{n_1}}}{{{\rm{d}}t}} = + {h_{{\rm{exc}}}}\sigma {n_0}-({k_{{\rm{fl}}}} + {k_{\rm{Q}}}){n_1}-{k_{{\rm{isc}}}}{n_1}\\ \frac{{{\rm{d}}{n_2}}}{{{\rm{d}}t}} = + {k_{{\rm{isc}}}}{n_1} - {k_{{\rm{ph}}}}{n_2} \end{array} \right. $ | (7) |
另外有归一化条件
GSD使用连续波激光作用工作光,在经过时间
| $ \left\{ \begin{array}{l} {n_0} = \frac{{{k_{{\rm{ph}}}}({k_{{\rm{fl}}}} + {k_{\rm{Q}}} + {k_{{\rm{isc}}}})}}{D}\\ {n_1} = \frac{{{h_{{\rm{exc}}}}\sigma {k_{{\rm{ph}}}}}}{D}\\ {n_2} = \frac{{{h_{{\rm{exc}}}}\sigma {k_{{\rm{isc}}}}}}{D} \end{array} \right. $ | (8) |
(8)式中
三重态寿命(磷光寿命)
目前,GSD显微镜已经实现纳米级分辨率成像[23].
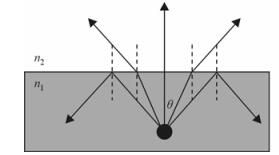
1.3 半球面镜(SIL)光线从光密介质射向光疏介质,入射角θ超过全反射角θm的部分会在交界面处发生全反射(total internal reflection)现象,如图 5.全反射角的大小为
|
| 图 5 全反射 Fig. 5 Total reflection |
| $ {\theta _m} = \arcsin \left( {\frac{{{n_2}}}{{{n_1}}}} \right) $ | (9) |
(9)式中n1和n2分别代表入射介质折射率和出射介质折射率.
在荧光成像的过程中,作为信息载体的荧光常常由于在样品表面全反射的问题而影响成像品质.如何克服荧光的全反射而提高荧光透射率,在经过多种尝试之后,人们发现将样品表面制作成半球形的光滑球面,通常称之为半球面镜(Solid Immersion Lens, SIL),是一种行之有效的方法.
早在1990年Mansfield S M和Kino G S就提出了SIL的概念[24].半球面镜大致结构如图 6所示,制作半球面镜时使荧光发射中心与半球面镜的球心重合,这么一来,便能顺利解决荧光在样品表面的全反射问题.实验上也已经证实[6],利用半球面镜可以提高荧光收集率,提高成像品质.

|
| 图 6 半球面镜 Fig. 6 Solid Immersion Lens |
2012年,Intel正式发布新一代22 nm工艺Atom处理器,而15 nm将是下一代CPU的发展目标.晶体管尺度不断减小,散热问题和量子效应影响到电子元器件的正常工作,集成度的提高举步维艰.
为了解决人们日益增长的更强计算能力的需求与电子计算机的性能眼看即将到达极限这二者之间的矛盾,各种采用不同计算模式的新型计算机模型方案逐步浮出水面,比如仿生的生机计算机、光子计算机以及量子计算机.
对量子计算的研究并不是在人们意识到经典计算机能力将达到极限之后才开始的.早在1959年,费曼(Feynman)在一次著名的演讲中提到量子计算的雏形概念[25].之后到20世纪80年代,费曼才真正意义上提出量子计算的优越性[26, 27].他提出在经典计算机上模拟量子力学系统存在本质困难,量子计算机依靠有效模拟其他量子系统的演化,可以做到很多经典图灵机做不到的事情.1985年,Deutsch D试图定义一种能够有效模拟任意物理系统的计算装置[28].他举出一个简单的例子,来说明量子计算机确实可能从计算能力上超过经典计算机,发展完善了量子图灵机模型,首次在形式上描述了量子计算机.1994年,量子计算领域第一个让全世界感到震惊的算法--Shor算法[29]被提出.Shor算法利用量子计算中的特有性质--量子并行性对分解大质数因子实现了指数加速,有效地解决了大质数难以被分解的问题,然而现在被广泛使用的RSA公钥加密算法正是建立在使用经典计算机难以分解大质数.这一算法的提出在信息领域引得轰然大波,也使得量子计算真正得到广泛关注.1996年,Grover L K提出量子搜索算法[30],经典情形需要由N次次操作才可以完成的搜索任务,量子搜索算法只需要次操作便可完成,提供了二次加速.
此外,还有众多量子算法被陆续提出,如量子Fourier变换算法和量子纠错算法[31, 32],不断完善量子计算理论.
2.2 金刚石NV色心金刚石中常含有各种掺杂元素,影响着其各种性质.氮(N)元素是金刚石中常见的掺杂元素之一.根据金刚石中含氮量的多少,通常可以把金刚石分为四类[33]:Type-Ⅰa,Type-Ⅰb,Type-Ⅱa和Type-Ⅱb;其含氮量由高到低.
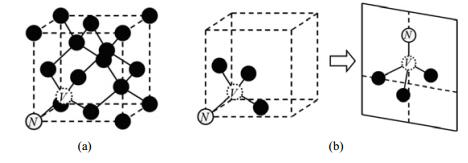
NV色心是由一个取代碳原子的氮(Nitrogen)原子和它邻近的一个空位(Vacancy)组成的.氮原子和与空位相邻的3个碳原子组成空间正四面体,空位位于正四面体的中心(如图 7).NV色心具有C3V对称性[34].
|
| 图 7 (a)金刚石NV色心;(b) NV色心的C3V对称性 Fig. 7 (a) NV center in diamond, (b) C3V Symmetry of NV center |
实验表明,NV色心具有两种价态:NV0和NV-;二者具有不同的荧光性质.NV0的零声子线(zero-phonon line,ZPL)为575 nm[35];而NV-的零声子线为637.2 nm[35-37].在自然界中,NV色心普遍以NV-的形式存在.本文中如无特别说明,所说NV色心都代指NV-.
NV-的形成是由NV色心额外捕获了金刚石中的一个电子.氮原子中的未成对电子与捕获的电子之间进行耦合,使得整体的电子自旋量子数为1,即S=1.这使得NV色心的电子基态成为自旋三重态,并且具有顺磁特性[38].
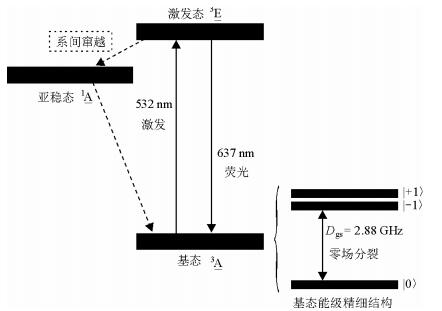
图 8所示为NV色心能级结构.NV色心的电子基态中ms=±1的这两个能级是简并的,它们与ms=±0能级之间存在零场分裂Dgs.NV色心基态的哈密顿量[33]可以写为
|
| 图 8 NV色心能级结构及荧光谱 Fig. 8 Energy Structure and fluorescence spectrum of NV center |
| $ H = {D_{{\rm{gs}}}}S_{\rm{z}}^2 + {g_{\rm{e}}}{\mu _{\rm{B}}}{B_{\rm{z}}}{S_{\rm{z}}} + {A_{{\rm{gs}}}}S \cdot I + QI_{\rm{z}}^2 + {g_{\rm{n}}}{\mu _{\rm{n}}}{B_{\rm{z}}}{I_{\rm{z}}} $ | (10) |
(10)式中ge和gn分别为电子与核的朗德g因子;基态零场分裂项Dgs=2.88 GHz;Bz为沿NV轴向(z方向)的外加磁场;S和Sz分别为电子自旋算符及其投影分量;I和Iz分别是核自旋算符及其投影分量;μB和μn分别为玻尔磁子和核磁子;基态超精细相互作用耦合系数Ags≈2.2 MHz;核四极矩分裂[39]Q ≈5 MHz.
由于超精细相互作用和应力作用比电子之间相互耦合作用小几个量级,故忽略掉它们带来的影响,只考虑到电子之间相互作用的精细结构.在基态与激发态之间至少存在一个亚稳态1A已经得到了证明[40],其能级寿命在百纳秒量级[39, 41].
通常将量子位(qubit)编码到NV色心基态中的ms=0能级和ms=±1两能级的二者之一上.目前一般认为,处于基态的电子吸收能量到达激发态之后,一部分电子通过自发辐射放出荧光的形式回到基态;还有一部分电子通过系间窜越(ISC)形式经过亚稳态回到基态中的能级上,这一过程不发出荧光.虽然具体过程还存在一定的争议[42, 43],但是通过激发光的持续作用,可以积累电子在ms=0能级上的布居数,实现量子比特的初始化;量子操作通过外加微波场完成;量子读出采用光读出[44],主要是利用了电子处于ms=±1两能级上时所发出的荧光会比电子处于ms=0能级上时弱约20%~40%[42, 43, 45].这即是所谓NV色心的光探测磁共振[46](Optically detected magnetic resonance,ODMR).
在激发光的照射下,NV色心可以产生很强并且稳定的荧光.在液氦温度下,发射谱在637 nm处有着十分尖锐的零声子线,伴有较宽的振动边带[47].随着温度的不断提高,由于声子效应的逐渐增强,零声子线被淹没在边带中.
相比于其他量子计算方案,NV色心固态量子计算方案有着独特优势[43]:
1. 金刚石样品容易得到.随机科学技术的不断发展以及人们对NV色心方案的密切关注,人们已经能够通过化学气相沉积(Chemical vapor deposition,CVD)方法合成金刚石,并通过离子束注入(Focused ion beam,FIB)方法注入氮离子以形成NV色心结构,且技术已经趋于成熟.
2. 单自旋量子比特.区别于NMR这类利用系综自旋作为研究对象的方法,NV色心体系的研究对象为单电子自旋.
3. 稳定的荧光性质以及单光子发射源.在强光长时间作用下,NV色心仍可能持续发出稳定荧光[18].
4. 较理想的退相干时间.在超纯样品中,甚至可以达到毫秒量级.
5. 利用共聚焦系统即可实现单自旋量子比特的初始化和读出,易实现.
6. 最重要的一点,室温下即可实现量子态制备、操纵和读出.其他多数备选方案的实验条件比较苛刻,操纵技术指标要求很高.在室温即能进行实验,大大提高了实验的可行度.
无论是量子算法,还是可扩展性,NV色心体系都有相关的实验进展.目前实验上已经实现了单比特量子Deutsch-Joza算法[48]、NV色心电子自旋量子态的非破坏性量子测量[49]、量子纠错算法[50].扩展性方面,NV色心周围的核自旋可以作为存储量子比特,且存储时间已经达到1 s[51];通过偶极相互作用的可扩展方案已经实现了2个NV色心、4个比特[52],基于飞行量子比特的可扩展方案也已实现[53].其中,基于偶极相互作用的可扩展方案比较容易实现,且2个NV色心之间的纠缠度高.这种扩展方案下,NV色心之间的距离(10 nm之内)远比光学衍射极限(200~300 nm)小,普通共聚焦光学上很难将几个NV色心的荧光分开,无法分别直接测量每个NV色心的量子状态,只能通过复杂的量子操控进行分别读出[52].这时,如果能够将光学分辨率提升至10 nm以下,对每个NV色心进行单独的光学定位和测量,则可以大大简化NV色心扩展后的状态读出过程.
2.3 研究现状NV色心是十分优秀的RESOFLT成像体系,它具有稳定的荧光发射能力[18].荧光染料往往会在高强度激光照射下发生“光漂白”现象而失去发出荧光的能力;相比之下,NV色心可以承受高强度,长时间的激光照射,并且稳定地发出荧光.
NV色心具有较容易达到的耗散光饱和功率Is[18],这得益于NV色心较长的平均荧光寿命
实验上共聚焦显微镜成像分辨率约为200 nm,目前已经多个实验小组能够利用STED方法分辨扫描共聚焦显微镜难以辨别的邻近NV色心.2009年,STED的提出者Hell S W所在的实验小组,利用脉冲STED的方法:使用532 nm绿光作为激发光,结合最大功率密度为
2010年,美国哈佛大学的Lukin M D实验小组,使用两台532 nm连续波激光器所发出的绿光分别作为激发光和STED光,成功分辨了两颗相距约150 nm的NV色心[19],图像分辨率达38 nm.之后结合微波操控技术,实现对邻近NV色心中单个色心的单独操控;并根据所得拉比振荡信号的不同可得出2个NV色心所处自旋环境不同的结论.
NV色心的GSD饱和功率密度约为数百kW/cm2,相较于NV色心的STED饱和功率密度小3个量级,因此,通常使用连续波模式的激光器即可实现高分辨成像.
2009年,Hell S W所在的实验小组分别利用两种GSD成像模式--普通模式和“负模式”完成了对NV色心的扫描成像[15].在负模式中,只利用到了一路532 nm的绿色激光,在饱和度
结合RESLOFT成像技术,NV色心的扫描成像分辨率已经纳米量级,相比与共聚焦显微镜的成像分辨率,已经取得了质的飞越.
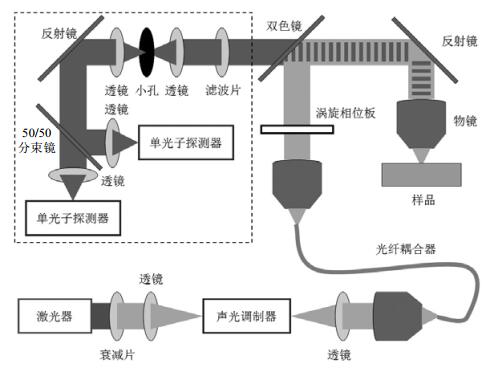
3 实验最新进展本实验室利用一路功率较强的绿色激发光束完成本实验.图 9所示为实验装置实物图;图 10为系统光路示意图.波长为532 nm的高斯型绿色激光由激光器发出,经过衰减片和透镜后到达声光调制器;之后依次经过光阑、透镜、光束扩散器到达光纤耦合器;激发光从光纤耦合器出来后,经由涡旋相位调节板[VPP]后形成所谓的“面包圈模式”(doughnut mode)激发光,之后再经过双色镜,1/2波片,物镜聚焦到实验所用样品上.

|
| 图 9 NV色心GSD成像实验平台 Fig. 9 Experimental Platform of GSD |
|
| 图 10 NV色心GSD成像系统光路(黑色虚线框内为收集光路) Fig. 10 Light path of GSD system |
NV色心受激发光影响而发光的荧光(637 nm,红色),由同一个物镜收集后,经过双色镜后进入收集“暗箱”;“暗箱”中依次放置着高通滤波片、聚汇透镜、小孔、发散透镜、荧光再经由一个50/50分束镜分别到达两个单光子探测器[APD]上.
采用上述GSD高分辨成像技术,实验室已获得了120 nm的NV色心横向成像分辨率;而实验室原所得NV色心横向最高分辨率为300 nm,所采用的是传统共聚焦显微成像技术.
区别于双光路正成像模式,本实验采用的是单一激发光路的负模式(negative mode)GSD成像方法,直接利用一路功率较强的激发光束经涡旋相位板后完成对金刚石中NV色心的扫描成像.如图 11所示,图 11(a)中的整个圆斑区域即为共聚焦显微镜下的NV色心大小,其尺寸约为300 nm;图 11(b)中心的浅色圆形区域则是GSD扫描成像中的NV色心尺寸大小,约为120 nm.从实验结果来看,较共聚焦显微镜扫描成像而言,分辨率已经得到了显著的提升.

|
| 图 11 NV色心共聚焦成像图(a)及GSD扫描图(b) Fig. 11 Confocal(a) and GSD(b) images from the same crystal region |
本文介绍了GSD超分辨成像技术在NV色心量子计算中的应用,简要分析了可逆饱和光学荧光跃迁技术中的STED显微镜和GSD显微镜的工作原理,并概述了金刚石NV色心固态量子计算中超分辨成像的相关最新研究进展.最后,通过单激发光路的GSD负模式成像方法,成功突破了衍射极限,达到了120 nm的分辨率.这些理论分析和实验结果将有助于今后的金刚石NV色心量子计算的超分辨技术和可扩展量子计算的研究.
| [1] | Abbe E . Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung[J]. Archiv für Mikroskopische Anatomie , 1873, 9 (1) : 413-468 DOI:10.1007/BF02956173 |
| [2] | Lewis A, Isaacson M, Harootunian A et al . Development of a 500-a spatial-resolution light-microscope. 1. Light is efficiently transmitted through gamma-16 diameter apertures[J]. Ultramicroscopy , 1984, 13 (3) : 227-231 DOI:10.1016/0304-3991(84)90201-8 |
| [3] | Pohl D W, Denk W, Lanz M . Optical stethoscopy-image recording with resolution lambda/20[J]. Appl Phys Lett , 1984, 44 (7) : 651-653 DOI:10.1063/1.94865 |
| [4] | Rugar D, Budakian R, Mamin H J et al . Single spin detection by magnetic resonance force microscopy[J]. Nature , 2004, 430 : 329-332 DOI:10.1038/nature02658 |
| [5] | Zwiller V, Bjork G . Improved light extraction from emitters in high refractive index materials using solid immersion lenses[J]. J Appl Phys , 2002, 92 (2) : 660-665 DOI:10.1063/1.1487913 |
| [6] | Siyushev P, Kaiser F, Jacques V et al . Monolithic diamond optics for single photon detection[J]. Appl Phys Lett , 2010, 97 (24) : 241902 DOI:10.1063/1.3519849 |
| [7] | Wilson T, Sheppard C J R . Theory and Practice of Scanning Optical Microscopy[M]. New York: Academic Press, 1984 . |
| [8] | Pawley J B . Handbook of Biological Confocal Microscopy[M]. New York: Springer, 2006 . |
| [9] | Hell S W, Stelzer E H K . Fundamental improvement of resolution with a 4Pi-confocal fluorescence microscope using two-photon excitation[J]. Opt Commun , 1992, 93 (5-6) : 277-282 DOI:10.1016/0030-4018(92)90185-T |
| [10] | Gustafsson M G L, Agard D A, Sedat J W . Sevenfold improvement of axial resolution in 3D widefield microscopy using two objective lenses[J]. Proc SPIE , 1995, 2412 : 147-156 DOI:10.1117/12.205334 |
| [11] | Hell S W, Wichmann J . Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy[J]. Opt Lett , 1994, 19 (11) : 780-782 DOI:10.1364/OL.19.000780 |
| [12] | Hell S W, Kroug M . Ground-state-depletion fluorscence microscopy: a concept for breaking the diffraction resolution limit[J]. Appl Phys B , 1995, 60 (5) : 495-497 DOI:10.1007/BF01081333 |
| [13] | Hell S W, Dyba M, Jakobs S . Concepts for nanoscale resolution in fluorescence microscopy[J]. Curr Opin Neurobiol , 2004, 14 (5) : 599-609 DOI:10.1016/j.conb.2004.08.015 |
| [14] | Heisenberg W . The Physical Principles of the Quantum Theory[M]. Chicago: Chicago Univ Press, 1930 . |
| [15] | Hell S W, Westphal V . Nanoscale resolution in the focal plane of an optical microscope[J]. Phys Rev Lett , 2005, 94 (14) : 143903 DOI:10.1103/PhysRevLett.94.143903 |
| [16] | Hell S W . Far-field optical nanoscopy[J]. Science , 2007, 316 (5828) : 1153-1158 DOI:10.1126/science.1137395 |
| [17] | Klar T A, Hell S W . Subdiffraction resolution in far-field fluorescence microscopy[J]. Opt Lett , 1999, 24 (14) : 954-956 DOI:10.1364/OL.24.000954 |
| [18] | Rittweger E, Han K Y, Irvine S E et al . STED microscopy reveals crystal colour centres with nanometric resolution[J]. Nature Photonics , 2009, 3 (3) : 144-147 DOI:10.1038/nphoton.2009.2 |
| [19] | Maurer P C, Maze J R, Stanwix P L et al . Far-field optical imaging and manipulation of individual spins with nanoscale resolution[J]. Nature Physics , 2010, 6 (11) : 912-918 DOI:10.1038/nphys1774 |
| [20] | Willig K I, Harke B, Medda R et al . STED microscopy with continuous wave beams[J]. Nat Methods , 2007, 4 (11) : 915-918 DOI:10.1038/nmeth1108 |
| [21] | Hell S W, Vicidomini G, Moneron G et al . Sharper low-power STED nanoscopy by time gating[J]. Nat Methods , 2011, 8 (7) : 571-575 DOI:10.1038/nmeth.1624 |
| [22] | Hell S W, Donnert G, Keller J et al . Macromolecular-scale resolution in biological fluorescence microscopy[J]. Proc Natl Acad, Sci USA , 2006, 103 (31) : 11440-11445 DOI:10.1073/pnas.0604965103 |
| [23] | Rittweger E, Wildanger D, Hell S W . Far-field fluorescence nanoscopy of diamond color centers by ground state depletion[J]. EPL , 2009, 86 : 14001 DOI:10.1209/0295-5075/86/14001 |
| [24] | Mansfield S M, Kino G S . Solid immersion microscope[J]. Appl Phys Lett , 1990, 57 : 2615-2616 DOI:10.1063/1.103828 |
| [25] | Feynman R P . There is plenty of room at the bottom[J]. Engineering and Science , 1960, 23 (5) : 22-36 |
| [26] | Feynman R P . Simulating physics with computers[J]. Int J Theor Phys , 1982, 21 (6) : 467-488 |
| [27] | Feynman R P . Quantum mechanical computers[J]. Optics News , 1985, 2 : 11-20 |
| [28] | Deutsch D . Quantum theory, the church-turing principle and the universal quantum computer[J]. Proc R Soc London Ser A , 1985, 400 (1818) : 97-117 DOI:10.1098/rspa.1985.0070 |
| [29] | Shor P W. Proceedings of the 35th annual symposium on the foundation of computer science[C]. Los Alamitos, IEEE Computer Society Press, 1994. |
| [30] | Grover L K . Quantum mechanics helps in searching for a needle in a haystack[J]. Phys Rev Lett , 1997, 79 (2) : 325 DOI:10.1103/PhysRevLett.79.325 |
| [31] | Nielsen M A, Chuang I L . Quantum computation and quantum information[M]. Cambridge: Cambridge University Press, 2000 . |
| [32] | Shor P W . Scheme for reducing decoherence in quantum computer memory[J]. Phys Rev A , 1995, 52 : R2493 DOI:10.1103/PhysRevA.52.R2493 |
| [33] | Popa I. Pulsed magnetic resonance on single defect centers in diamond[D]. Stuttgart, University of Stuttgart, 2006. |
| [34] | Lenef A, Rand S C . Electronic structure of the n-v center in diamond: Theory[J]. Phys Rev B , 1996, 53 : 13441 DOI:10.1103/PhysRevB.53.13441 |
| [35] | Gaebel T, Domhan M, Wittmann C et al . Photochromism in single nitrogen-vacancy defect in diamond[J]. Appl Phys B , 2006, 82 (2) : 243-246 |
| [36] | Mita Y . Change of absorption spectra of type-ib diamond with heavy neutron irradiation[J]. Phys Rev B , 1996, 53 : 11360 DOI:10.1103/PhysRevB.53.11360 |
| [37] | Goss J P, Jones R, Briddon P R et al . Comment on "electronic structure of the n-v center in diamond: Theory"[J]. PhysRev B , 1997, 56 : 16031-16032 |
| [38] | Jelezko F, Popa I, Gruber A et al . Single spin states in a defect center resolved by optical spectroscopy[J]. Appl Phys Lett , 2002, 81 : 2160-2162 DOI:10.1063/1.1507838 |
| [39] | Steiner M, Neumann P, Beck J et al . Universal enhancement of the optical readout fidelity of single electron spins at nitrogen-vacancy centers in diamond[J]. Phys Rev B , 2010, 81 : 035205 DOI:10.1103/PhysRevB.81.035205 |
| [40] | Doherty M W, Manson N B, Delaney P et al . The negatively charged nitrogen-vacancy centre in diamond: the electronic solution[J]. New J Phys , 2009, 13 : 025019 |
| [41] | Neumann P, Kolesov R, Jacques V et al . Excited-state spectroscopy of single NV defects in diamond using optically detected magnetic resonance[J]. New J Phys , 2009, 11 : 013017 DOI:10.1088/1367-2630/11/1/013017 |
| [42] | Manson N B, Harrison J P, Sellars M J . Nitrogen-vacancy center in diamond: Model of the electronic structure and associated dynamics[J]. Phys Rev B , 2006, 74 : 104303 DOI:10.1103/PhysRevB.74.104303 |
| [43] | Warchtrup J, Jelezko F . Processing quantum information in diamond[J]. J Phys: Condens Matter , 2006, 18 : S807-S824 DOI:10.1088/0953-8984/18/21/S08 |
| [44] | Van Oort E, Manson N B, Glasbeek M . Optically detected spin coherence of the diamond N-V centre in its triplet ground state[J]. J Phys C: Solid State Phys , 1988, 21 : 4385 DOI:10.1088/0022-3719/21/23/020 |
| [45] | Gruber A, Dräbenstedt A, Tietz C et al . Scanning confocal optical microscopy and magnetic resonance on single defect centers[J]. Science , 1997, 276 : 2012-2014 DOI:10.1126/science.276.5321.2012 |
| [46] | Childress L I. Coherent manipulation of single quantum systems in the solid state[D]. Massachusetts: Harvard University.2007. |
| [47] | Jelezko F, Wrachtrup J . Single defect centres in diamond: A review[J]. Phys Stat Sol , 2006, 203 (13) : 3207-3225 DOI:10.1002/pssa.v203:13 |
| [48] | Shi F, Rong X, Xu N et al . Room-temperature implementation of the deutsch-jozsa algorithm with a single electronic spin in diamond[J]. Phys Rev Lett , 2010, 105 : 040504 DOI:10.1103/PhysRevLett.105.040504 |
| [49] | Neumann P, Beck J, Steiner M et al . Single-shot readout of a single nuclear spin[J]. Science , 2010, 329 : 542-544 DOI:10.1126/science.1189075 |
| [50] | Waldherr G, Wang Y, Zaiser S et al . Quantum error correction in a solid-state hybrid spin register[J]. Nature , 2014, 506 : 204-207 DOI:10.1038/nature12919 |
| [51] | Maurer P C, Kucsko G, Latta C et al . Room-temperature quantum bit memory exceeding one second[J]. Science , 2012, 336 : 1283-1286 DOI:10.1126/science.1220513 |
| [52] | Dolde F, Jakobi I, Naydenov B et al . Room-temperature entanglement between single defect spins in diamond[J]. Nat Phys , 2013, 9 : 139-143 DOI:10.1038/nphys2545 |
| [53] | Bernien H, Hensen B, Pfaff W et al . Heralded entanglement between solid-state qubits separated by three metres[J]. Nature , 2013, 497 : 86-90 DOI:10.1038/nature12016 |
 2014, Vol. 31
2014, Vol. 31