波谱学杂志  2014, Vol. 31 Issue (3): 321-330
|
梯度回波(gradient echo，GRE)序列是磁共振成像(magnetic resonance imaging，MRI)中常用的脉冲序列，已广泛应用于临床医学诊断和科学研究，如三维高分辨结构成像、动态对比增强MRI、磁共振血管成像、组织灌注及功能MRI等[1].此外，利用梯度回波序列的多回波信号衰减，可计算得到T2定量图；采用T2加权梯度回波扫描的相位信息可显示常规模图上无法显示或显示不清的脑部结构，如深部脑核团和白质纤维束[2]、活体灰质皮层的分层结构[3, 4]；利用相位的定量信息还可进一步得到磁敏感加权成像和定量磁化率成像，可用于诊断颅内出血和研究帕金森病、阿尔茨海默病、多发性硬化、Hallevorden-Spatz综合症等疾病脑铁含量的变化[5-10].
梯度回波序列尤其是长回波时间梯度回波，对主磁场波动非常敏感，因此对主磁场的稳定性有较高要求[11].影响主磁场稳定性的因素有很多，其中一个重要因素是人体生理运动，包括呼吸、心跳、血液及脑脊液的流动等.尤其在呼吸运动过程中，人体的一些组织结构（如胸腔、横隔膜、内脏、肩膀和手臂等）的位置和氧含量随时间周期性变化，导致主磁场在空间和时间上相应作周期性改变.在3 T场强下，呼吸运动导致的脑组织局部磁场有0.01 ppm（约为1.25 Hz）的波动[12, 13].在脑功能磁共振成像中，采用单次激发回波平面成像(EPI)序列，每隔2~3 s左右采集一帧图像，呼吸运动会引起图像信号周期性波动，最终导致错误的功能区激活[14].在三维多回波梯度回波中，这种波动会影响整个扫描过程，导致图像产生伪影.
为了降低呼吸运动对脑功能成像的影响，可采用下述补偿技术：在颅脑内主磁场的变化近似均匀，因此可利用导航回波整体矫正呼吸伪影[19]；在单次激发EPI序列中，采集一幅图像的时间为几十毫秒，远小于呼吸周期，可假设每幅图像是在同一个时间点上采集，对图像域中的像素进行回顾性矫正[15]；也可通过优化采集并进行空间平滑、不断调整匀场线圈的电流等前瞻性的方法来降低呼吸运动伪影[16, 17].
本文在三维多回波梯度回波的基础上，采用导航回波获取呼吸运动导致的局部磁场波动，用以矫正图像回波中随时间变化的相位波动，并将该技术应用于T2定量图研究.
1 材料和方法10例健康志愿者参与该项研究，其中男性和女性各5例，年龄在21~26岁之间.所有扫描均在3 T MRI（西门子MAGNETOM Trio a Tim 3 T）设备上完成，系统软件版本为syngo MR VB17，采用大体线圈作为信号发射线圈，采用12通道头线圈作为信号接收线圈.
1.1 模型建立为了模拟人体呼吸运动导致的颅脑局部磁场变化，可建立如下模型[18]：用圆筒状的水代表人体躯干，用球形的顺磁性气囊（大小和位置可变）代表肺.令Z轴平行于主磁场方向B0，即人体的头脚方向. XY平面为横断面，其中Y轴沿人体的前后方向.根据该模型，可推导出由呼吸引起的颅脑部位局部磁场变化（ΔB）为：
| $\Delta B(x, y, z) = \frac{{\Delta \chi {B_0}{R^3}}}{3}{\rm{ }}\frac{{[2{{(z-{z_0})}^2}-{{(x-{x_0})}^2} - {{(y - {y_0})}^2}]}}{{{{[{{(x-{x_0})}^2} + {{(y-{y_0})}^2} + {{(z-{z_0})}^2}]}^{5/2}}}}$ | (1) |
(1)式中R是球体的半径，
考虑到颅脑的大小相对于颅脑到肺的距离较小，因此呼吸运动引起的
| $\Delta \Phi (\tau ) = \gamma {\kern 1pt} \Delta {B_0}\tau + \Delta {\Phi _{\, 0}}$ | (2) |
(2)式中τ是射频脉冲激发后的演化时间，
| $\Delta \Phi (TE) \approx \gamma {\kern 1pt} \Delta {B_{0\, }}TE$ | (3) |
(3)式中TE为回波时间.
1.2 脉冲序列的实现集成有导航回波的三维多回波梯度回波序列于西门子公司的序列集成开发平台IDEA上实现，脉冲时序图如图 1所示.所有频率编码梯度均为相同极性，以避免场不均匀导致的回波中心不一致[20].第一个回波作为导航回波，未施加相位编码梯度；从第二个回波起作为不同回波时间的成像回波，均需施加层方向上和相位编码方向上的相位编码梯度.当观察呼吸运动导致的不同TE的回波信号相位变化时，未施加选层方向上和相位编码方向上的相位编码梯度.
|
| 图 1 集成有导航回波的三维多回波梯度回波脉冲序列时序图 Fig. 1 Schematic of 3D multiecho gradient echo sequence with an additional navigator echo |
三维多回波梯度回波的扫描参数设置为：重复时间(TR)=60 ms，导航回波的回波时间(TE)为6 ms，图像回波的TE分别为12 ms / 18 ms / 24 ms / 30 ms / 36 ms / 42 ms / 48 ms，翻转角(FA)=15°，观察野(FOV)=240 mm×240 mm，层厚(slice thickness)=2 mm，层数(slice per slab)=32，层方向上过采(slice oversampling)=12.5 %，扫描矩阵(matrix)=256×256（频率编码×相位编码），相位编码方向为左右方向，扫描时间为9 min 13 s.
当观察呼吸运动导致的不同TE的回波信号相位变化时，扫描参数为：层厚=5 mm，扫描矩阵=64×64，其他参数与上述三维多回波梯度回波一致，扫描时间为54 s.
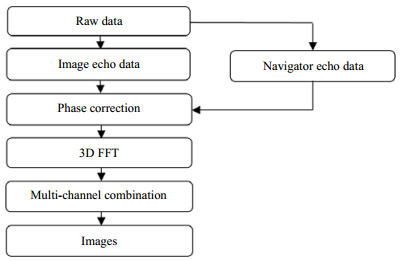
1.4 数据处理和分析 1.4.1 图像重建图像重建流程图如图 2所示.首先，将原始数据分为图像回波数据和导航回波数据两部分；然后，利用导航回波的信息对图像回波的数据进行相位矫正；接下来，对相位矫正后的原始数据进行三维傅里叶变换；最后，将所有通道的图像采用均方根组合[21]，得到组合图像.
|
| 图 2 图像重建流程图 Fig. 2 Diagram of image reconstruction process |
相位矫正是利用导航回波和图像回波之间的相位相关性来对成像k空间数据的相位进行矫正[22]. 8个回波采集有48 ms的时间间隔，相对于人的呼吸周期（3 s左右）是很短的，因此可近似认为呼吸导致的
| ${S'_{{\rm{image}}}} = {S_{{\rm{image}}}}\exp (-i\gamma {\kern 1pt} \Delta {B_0}T{E_{{\rm{image}}}})$ | (4) |
(4)式中
在三维多回波梯度回波序列中，信号是按T2指数衰减的：
| $M = {M_0}{{\rm{e}}^{(-t/T_2^*)}} + N$ | (5) |
(5)式中M是t时刻接收到的信号，M0是射频脉冲过后初始磁化强度矢量在横向的最大值，N是噪声，T2是横向弛豫时间.对于图像空间每个像素，采用Levenberg-Marquardt非线性最小二乘法拟合不同回波时间点的数据可得到T2值.
1.4.3 伪影矫正效果评价分别计算相位矫正前后的伪影大小，用以评价伪影矫正效果.在计算伪影大小时，选取3个感兴趣区(Region of Interesting，ROI)，如图 3所示，ROI#1同时包含伪影和背景噪声，ROI#2只包含背景噪声，ROI#3只包含颅脑组织.伪影大小(Artifacts Level，AL)的定量计算方法如下[25]：
| $AL = (mean1-mean2)/mean3$ | (6) |
|
| 图 3 用以伪影大小计算的3个感兴趣区 Fig. 3 Three ROIs regions to evaluate artifact level |
(6)式中mean1，mean2，mean3分别为ROI#1，ROI#2，ROI#3的区域内所有像素信号平均值.
2 结果与讨论图 4是一例健康志愿者颅脑采用梯度回波序列采集得到的不同TE的回波相位随相位编码步数的变化图[(a)，相位矫正前；(b)，相位矫正后]. 图 4(a)中8个回波的相位变化周期一致，约为3.3 s，与人正常的呼吸周期相符.相位波动幅度随着TE的增长而增大，至第8个回波(TE=48 ms)的相位波动约为±0.2 rad，根据(3)式可推导出呼吸运动导致的颅脑部位主磁场波动为±1.32 Hz，此与文献报道的结果相近[12, 13]. 图 4(b)显示，采用第一个回波的相位对所有回波的相位进行矫正后，相位随时间的波动幅度很小，呼吸运动引起的相位波动得到有效去除.
|
| 图 4 8个回波的相位随相位编码步数的变化[(a)矫正前；(b)矫正后] Fig. 4 The phase fluctuation of eight echoes with respect to the phase encoding number [(a) before correction; (b) after correction] |
图 5是一例健康志愿者采用同一层面矫正前后得到的不同TE的颅脑横断面图像.图 5(a)为矫正前的颅脑图，在相位编码方向（左右方向）可见明显的呼吸伪影，而且随TE的增长，伪影更加明显.对TE为48 ms的图像右前额叶区域进行局部放大，可见白质和灰质的分界面模糊不清，白质部分信号空间分布明显不均匀. 图 5(b)为矫正后的颅脑图，可见伪影得到有效去除，灰白质分界面清晰，前额叶区域白质信号空间分布均匀. 10例健康志愿者均得到上述类似结果.
|
| 图 5 同一层面的不同回波时间的颅脑横断面图像[(a)矫正前；(b)矫正后] Fig. 5 Axial brain images of the same slice with different echo time [(a) before correction; (b) after correction] |
图 6是一例健康志愿者由多回波梯度回波图像采用Levenberg-Marquardt算法拟合得到的T2定量图. 图 6(a)是由未矫正数据后处理得到的T2定量图，呼吸运动导致前额叶区域出现明显深浅相间的条纹（图中标记的圆圈内）. 图 6(b)是对原始数据相位矫正后后处理得到的结果，可见前额叶区域信号分布均匀（图中标记的圆圈内）.
|
| 图 6 T2定量图[(a)矫正前；(b)矫正后] Fig. 6 T2 mapping [(a) before correction; (b) after correction] |
图 7是根据(6)式对所有健康志愿者进行伪影水平的计算与统计结果图.不同信号区和伪影区的选择对伪影水平计算有较大影响，因此本文对所有被试的所有层面都采用同一个蒙片，每个被试的伪影水平为所有层的平均值，此可减少人为选取区域的影响.考虑到男性多为腹式呼吸，女性多为胸式呼吸，不同的呼吸方式可能对局部磁场的影响不一样，因此男性和女性分开统计.由统计结果可见:随着TE的增长，伪影水平几乎呈线性升高；相位矫正后，图像伪影水平均得到显著性下降（女性：p=0.003，男性：p=0.006），矫正效果随着TE的增长而明显.统计结果还显示，男女呼吸伪影水平有显著性差异(p < 0.000 5)，女性的呼吸运动导致的伪影更明显.
|
| 图 7 矫正前后伪影水平统计结果[(a)女性；(b)男性] Fig. 7 Statistical result of artifacts level before correction and after correction [(a) female; (b) male] |
本文主要报道了采用导航回波可有效矫正呼吸运动导致的多回波梯度回波图像的伪影，该方法应用T2定量图呼吸伪影的矫正，具有较好的效果.该方法对基于多回波梯度回波序列的成像方法均适用，因此具有较广泛的应用.如近年来发展起来的磁敏感加权成像和定量磁化率成像均利用梯度回波的相位信息获取局部磁场的变化，可采用单回波或多回波方法.多回波方法数据采样率更高，得到的图像信噪比和对噪比更高；另外，多回波方法采用更大的采样带宽，几何形变更小[26-29]，而且多回波在时域的演化信息能增强相位去折叠方法的可靠性[30-32].因此导航回波矫正方法可应用于磁敏感加权成像和定量磁化率成像.
文中的导航回波矫正方法基于的理论模型认为，呼吸运动引起的局部磁场在颅脑内近似均匀[19]，但实际上呼吸运动引起的局部磁场变化在空间分布并不均匀[11].因此，可尝试做进一步的矫正，提高伪影矫正水平.本文采用的三维多回波梯度回波未使用并行成像，所以成像时间较长，但本文的方法是对原始数据进行相位矫正，因此可用于并行成像数据的矫正.
3 结论呼吸运动可引起颅脑局部磁场波动，从而导致梯度回波图像产生伪影.采用导航回波方法能有效矫正呼吸运动导致的相位波动，去除伪影.
| [1] | Frahm J, Haase A, Matthaei D . Rapid NMR imaging of dynamic processes using the FLASH technique[J]. Magn Reson Med , 1986, 3 (2) : 321-327 DOI:10.1002/(ISSN)1522-2594 |
| [2] | Rauscher A, Sedlacik J, Barth M et al . Magnetic susceptibility-weighted MR phase imaging of the human brain[J]. AJNR Am J Neuroradiol , 2005, 26 (4) : 736-742 |
| [3] | Duyn J H, van Gelderen P, Li T Q et al . High-field MRI of brain cortical substructure based on signal phase[J]. Proc Natl Acad Sci USA , 2007, 104 (28) : 11796-11801 DOI:10.1073/pnas.0610821104 |
| [4] | Fukunaga M, Li T Q, van Gelderen P et al . Layer-specific variation of iron content in cerebral cortex as a source of MRI contrast[J]. Proc Natl Acad Sci USA , 2010, 107 (8) : 3834-3839 DOI:10.1073/pnas.0911177107 |
| [5] | Grabner G, Dal-Bianco A, Schernthaner M et al . Analysis of multiple sclerosis lesions using a fusion of 3.0 T FLAIR and 7.0 T SWI phase: FLAIR SWI[J]. J Magn Reson Imag , 2011, 33 (3) : 543-549 DOI:10.1002/jmri.v33.3 |
| [6] | Haacke E M, Makki M, Ge Y et al . Characterizing iron deposition in multiple sclerosis lesions using susceptibility weighted imaging[J]. J Magn Reson Imag , 2009, 29 (3) : 537-544 DOI:10.1002/jmri.v29:3 |
| [7] | Lotfipour A K, Wharton S, Schwarz S T et al . High resolution magnetic susceptibility mapping of the substantia nigra in Parkinson's disease[J]. J Magn Reson Imag , 2012, 35 (1) : 48-55 DOI:10.1002/jmri.v35.1 |
| [8] | Zhang J, Zhang Y, Wang J et al . Characterizing iron deposition in Parkinson's disease using susceptibility-weighted imaging: an in vivo MR study[J]. Brain Res , 2010, 1330 : 124-130 DOI:10.1016/j.brainres.2010.03.036 |
| [9] | Zhang W, Sun S G, Jiang Y H et al . Determination of brain iron content in patients with Parkinson's disease using magnetic susceptibility imaging[J]. Neurosci Bull , 2009, 25 (6) : 353-360 DOI:10.1007/s12264-009-0225-8 |
| [10] | Zhu W Z, Zhong W D, Wang W et al . Quantitative MR phase-corrected imaging to investigate increased brain iron deposition of patients with Alzheimer disease[J]. Radiology , 2009, 253 (2) : 497-504 DOI:10.1148/radiol.2532082324 |
| [11] | Klassen L M, Menon R S . Robust automated shimming technique using arbitrary mapping acquisition parameters (RASTAMAP)[J]. Magn Reson Med , 2004, 51 (5) : 881-887 DOI:10.1002/(ISSN)1522-2594 |
| [12] | Wowk B, McIntyre M C, Saunders J K . k-Space detection and correction of physiological artifacts in fMRI[J]. Magn Reson Med , 1997, 38 (6) : 1029-1034 DOI:10.1002/(ISSN)1522-2594 |
| [13] | Henry P G, van de Moortele P F, Giacomini E et al . Field-frequency locked in vivo proton MRS on a whole-body spectrometer[J]. Magn Reson Med , 1999, 42 (4) : 636-642 DOI:10.1002/(ISSN)1522-2594 |
| [14] | Hu X, Kim S G . Reduction of signal fluctuation in functional MRI using navigator echoes[J]. Magn Reson Med , 1994, 31 (5) : 495-503 DOI:10.1002/(ISSN)1522-2594 |
| [15] | Glover G H, Li T Q, Ress D . Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR[J]. Magn Reson Med , 2000, 44 (1) : 162-167 DOI:10.1002/(ISSN)1522-2594 |
| [16] | Triantafyllou C, Hoge R D, Wald L L . Effect of spatial smoothing on physiological noise in high-resolution fMRI[J]. Neuroimage , 2006, 32 (2) : 551-557 DOI:10.1016/j.neuroimage.2006.04.182 |
| [17] | van Gelderen P, de Zwart J A, Starewicz P et al . Real-time shimming to compensate for respiration-induced B0 fluctuations[J]. Magn Reson Med , 2007, 57 (2) : 362-368 DOI:10.1002/(ISSN)1522-2594 |
| [18] | Raj D, Paley D P, Anderson A W et al . A model for susceptibility artefacts from respiration in functional echo-planar magnetic resonance imaging[J]. Phys Med Biol , 2000, 45 (12) : 3809-3820 DOI:10.1088/0031-9155/45/12/321 |
| [19] | Van de Moortele P F, Pfeuffer J, Glover G H et al . Respiration-induced B0 fluctuations and their spatial distribution in the human brain at 7 Tesla[J]. Magn Reson Med , 2002, 47 (5) : 888-895 DOI:10.1002/(ISSN)1522-2594 |
| [20] | Ericsson A, Weis J, Hemmingsson A et al . Measurements of magnetic field variations in the human brain using a 3D-FT multiple gradient echo technique[J]. Magn Reson Med , 1995, 33 (2) : 171-177 DOI:10.1002/(ISSN)1522-2594 |
| [21] | Huang Min(黄敏), Cheng Jun-bo(陈军波), Xiong Qiong(熊琼) et al . Comparison and implementation of commonly-used image reconstruction algorithms in parallel MRI(并行MRI图像重建算法比较及软件实现)[J]. Chinese J Magn Reson(波谱学杂志) , 2011, 28 (1) : 99-108 |
| [22] | Wang Qian-feng(王前锋), Li Jian-qi(李建奇), Wu Dong-mei(吴东梅) . Implementation of high resolution diffusion weighted imaging of small animal in clinical MRI system(小动物高分辨扩散加权成像在临床MRI上的实现)[J]. Chinese J Magn Reson(波谱学杂志) , 2012, 29 (3) : 372-378 |
| [23] | Jiang Xiao-ping(姜小平), Li Jian-qi(李建奇), Fan Ming-xia(范明霞) . Line-scan diffusion tensor imaging on low field strenth MRI scanner(低场MRI系统中线扫描扩散张量成像方法的研究)[J]. Chinese J Magn Reson(波谱学杂志) , 2008, 25 (4) : 470-477 |
| [24] | Chen Wei-bo(陈伟波), Li Jian-qi(李建奇), Jiang Xiao-ping(姜小平) . Implementation of self-navigated motion correction fast spin echo technique at Low field MRI system(自导航快速自旋回波在低场MRI上的实现)[J]. Chinese J Magn Reson(波谱学杂志) , 2009, 26 (2) : 197-205 |
| [25] | Peeters J M, Fuderer M . SENSE with improved tolerance to inaccuracies in coil sensitivity maps[J]. Magn Reson Med , 2013, 69 (6) : 1665-1669 DOI:10.1002/mrm.24400 |
| [26] | Yao B, Li T Q, Gelderen P et al . Susceptibility contrast in high field MRI of human brain as a function of tissue iron content[J]. Neuroimage , 2009, 44 (4) : 1259-1266 DOI:10.1016/j.neuroimage.2008.10.029 |
| [27] | Denk C, Rauscher A . Susceptibility weighted imaging with multiple echoes[J]. J Magn Reson Imag , 2010, 31 (1) : 185-191 DOI:10.1002/jmri.21995 |
| [28] | Gilbert G, Savard G, Bard C et al . Quantitative comparison between a multiecho sequence and a single-echo sequence for susceptibility-weighted phase imaging[J]. Magn Reson Imag , 2012, 30 (5) : 722-730 DOI:10.1016/j.mri.2012.02.008 |
| [29] | Luo J, Jagadeesan B D, Cross A H et al . Gradient echo plural contrast imaging-signal model and derived contrasts: T2, T1, Phase, SWI, T1f, FST2 and T2-SWI[J]. Neuroimage , 2012, 60 (2) : 1073-1082 DOI:10.1016/j.neuroimage.2012.01.108 |
| [30] | Liu T, Surapaneni K, Lou M et al . Cerebral microbleeds: Burden assessment by using quantitative susceptibility mapping[J]. Radiology , 2012, 262 (1) : 269-278 DOI:10.1148/radiol.11110251 |
| [31] | Schweser F, Deistung A, Lehr B W et al . Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: An approach to in vivo brain iron metabolism?[J]. Neuroimage , 2011, 54 (4) : 2789-2807 DOI:10.1016/j.neuroimage.2010.10.070 |
| [32] | Feng W, Neelavalli J, Haacke E M . Catalytic multiecho phase unwrapping scheme (CAMPUS) in multiecho gradient echo imaging: Removing phase wraps on a voxel-by-voxel basis[J]. Magn Reson Med , 2013, 70 (1) : 117-126 DOI:10.1002/mrm.v70.1 |
